浅谈中职数学中函数概念的建立

陈定发

（云南省轻工业学校，云南 昆明 650216）

浅谈中职数学中函数概念的建立

陈定发

（云南省轻工业学校，云南 昆明 650216）

本文通过函数概念的重温、保持、再现三个阶段实现函数概念的建立，让学生从本质上理解函数概念，使函数概念融入到学生已有的认知结构中，形成了系统的认知结构，促进了学习的迁移。

函数；建立；学习；再现

函数概念是数学中一个非常重要的概念，它标志着常量数学向变量数学的迈进，是常量数学到变量数学的过度阶段。函数概念的学习是一个循序渐进的过程，在初中，学生已对函数概念有了一定的了解。它是刻画客观世界的一个重要数学模型；它为我们解决日常生活和其他学科的问题提供了有效的思维方式和手段。因此函数在中职阶段具有及其重要的地位，而学生要从本质上理解掌握函数概念就得摒弃以往的被动接受的学习方式，采用主动、合理的学习方式，达到理解、掌握、应用函数思想解决问题的目的。本文将从以下三方面来阐述函数概念的教学：

1 函数概念建立阶段

学生学习新知识时，如果能和他们已有的数学知识相联系，通过认知主体积极的发现活动，将会有利于新知识体系的建构。所以对于函数概念，我们可以列举生活中学生熟悉的、学生感兴趣的、能够被学生所理解的实例，让学生对函数概念先产生感知，然后再通过对实例的观察、分析、讨论，初步达到认识、理解函数概念。

首先，我们可以通过学生生活中所熟悉的事物来引入函数概念，使学生在已有生活经验的基础上对函数概念形成感知表象。下面就是引入函数概念很好的例子。

1.1 课前让学生测量当地一天各个时段的气温填入下表，然后画出曲线图：（表1）

表1

此例通过实践来探索和感知事物的变化，认识气温与时间之间的变化关系，把数学的学习与我们的实际生活紧密联系起来，调动了学生学习的积极性与主动性。为函数概念的认识作好铺垫，同时也为函数的表示法埋下伏笔。

其次，有了上面感性认识的基础，如果再通过创设生动有趣地学习情境，那么就能使学生在观察、动手实践过程中感知、领会函数概念，实现知识的存储、记忆，最终形成恰当的心理表征。下面是一个很好的体现函数概念与表示法的例子。

例1.宋朝时，有一个杂货店出售一种干菜，每斤2元，有一天老板外出，只有不会算帐的老板娘在家，怎么办呢？老板灵机一动，想了一个办法，建立下表：（表2）

表2

老板娘对照此表格就可以卖菜。

有人知道了老板娘的底细，故意为难她，问买2.5斤的干菜需多少钱呢？老板娘一听，愣住了。老板回来后又想出了一个办法，他画了这样一幅图：老板娘对照此图又开心的卖菜了。

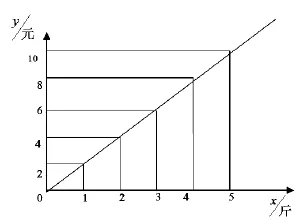
通过上述例子，让学生通过表格与图像的形式来认识函数概念中两个变量之间的关系。由于它具体而有趣味，能够加深学生对函数概念的认识并激发学生学习的动机。如果我们将这个例子进一步拓展，让学生通过上述的表格与图像研究购买干菜的量用x表示与所需金额用y表示，这样学生认知函数概念时就很容易从表格与图像过渡到函数的解析式，通过具体的表格与图像来理解解析式的意义。这一过程体现出函数概念的学习从具体到抽象的过程。

以上的情景创设、教师的引导与学生对函数概念的主动建构，加深了学生对函数概念的认识与理解，并让学生掌握函数的三种表示方法：解析法、列表法和图像法及这三种表示法之间的相互转换。

2 函数概念保持阶段

温故而知新，学习具有积累性。数学的学习过程是一个螺旋上升的过程，是不断“实践——理论——实践”的过程，只有通过反复的练习、实践才能促进知识的理解、掌握，也增强知识的保持。

通过上面的学习，学生对函数概念已有了一定的认识，在函数概念学习的基础上，将学生学得的信息经过复述、强化后，让函数概念的理解与掌握进入一个长时记忆的过程，并有效的加以存储，为学生学习函数概念灵活掌握与应用奠定坚实的基础。所以将通过以下步骤来实现函数概念的保持。

2.1 通过具体实例来加深学生对函数概念的理解促进知识的保持。例如：

2.1.1 请你举出生活中的函数实例，并说明理由。

例如：公路上汽车的行驶时间与所走过的路程之间的关系就是一种函数关系。

应用此例可以使学生主动思考，调动学生学习的积极性，同时也是函数概念的初步认识作用于实践的过程，这有利于检验学生对函数概念的理解程度。

2.1.2 下列变化关系中，哪些y是x的函数？哪些不是？并说明理由。

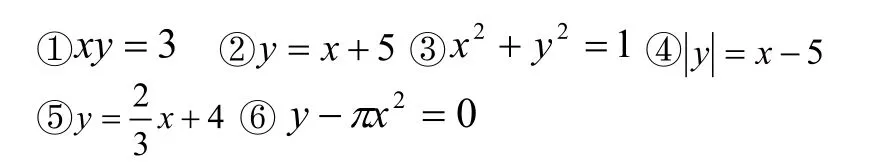
研究表明正反样例的应用是突出概念本质特征与非本质特征的有效手段，所以本例通过正反样例的使用，使学生在练习中领会函数概念的本质属性，深化函数认知。

2.2 根据所给图像或表格对简单实际问题中的函数关系进行分析，在应用与反思中促进概念的保持。

（1） b =＿＿ ， k =＿＿ 。（2）当时x=30时， y =＿＿ 。（3）当时y=30时， x =＿＿ 。

（2）你能写出x与y之间的关系式吗？

这样使学生在解决实际问题、学习具体函数知识的过程中体会出“数形结合”的重要数学思想，从而达到增强理解，深化认知，促进保持的目的。

3 函数概念再现阶段

通过以上对函数概念的感知、领会、保持，使学生对函数有了更深、更系统的认识与理解，形成了一定的认知经验，而这些认知经验只有通过概括、整理之后才能纳入自己的认知结构中，才能实现有意义的建构。而概括、整理过程其实是一个提取有效信息的过程，教师必须让学生在不同的情境中进行学习，并为学生提供在不同情境中提取信息过程的机会；同时更为重要的是，要引导学生概括和掌握其中的原理和原则，从复杂的实际问题中提取有效信息，形成解决问题的数学思维，最终达到促进学习迁移的目的。因此教师所呈现的作业、练习时必须注意题型的丰富性、多样性、层次性，以便符合不同层次学生的需要，从而强化其学习动机，促进知识的建构。老师要引导学生用自己的语言概括总结出所学知识的关键信息及对所学知识的理解，通过概括、练习、反馈等方式，达到再现函数本质、强化函数概念、促进学习迁移的目的。

通过由浅显的问题解决到应用相同的思路和方法解决复杂实际问题，进一步加深对函数的认知。引导学生建立恰当的函数模型，促进知识的反馈和迁移。

通过下面的例子来体现函数概念的再现。

例：为了保护学生的视力，课桌椅的高度都是按一定的关系配套设计的，研究表明：假设课桌的高度为ycm，椅子面的高度为xcm，它们存在着某种联系，经过收集数据。得到下表：

（1（请确定y与x的函数关系式。

（2（现有一把高35cm的椅子和一张高66.5cm的课桌，把它们配套是否符合条件？请通过计算说明理由。

此题从表面上看较复杂，实际上只要学生描出图像，就很容易猜想出所求的函数关系，再根据给出的数据加以验证就可以肯定这是一个一次函数。解决这道题目的关键是学生对一次函数已经形成稳定的认知结构，很容易在一次函数关系的表格、图像与解析式之间进行转换。当然，这是建立在前一阶段的基础之上。若学生解决这一问题时有困难，教师加以引导即让学生学会函数关系在列表、图像与解析式之间进行转换。通过这样的过程，学生很快就学会将这种思路和方法迁移到其他的函数关系中。

函数主要是研究变量与变量之间的对应关系，它是解决生活、生产中实际问题的重要数学工具之一。函数知识的学习、理解和掌握是一个螺旋式上升的过程。学好函数知识将为以后学习其他课程奠定坚实的认知基础。

［1］吴庆麟 ，教育心理学， 华东师范大学出版社，2006

［2］李广全 ，数学（基础模块（上册，高等教育出版社，2013

［3］陈平，建构主义思想指导数学概念教学，保定师范专科学校学报，2003

G633.6

A

1003-5168（2015）11-271-02