考虑地质及开发因素约束的三角形井网优化
2015-10-17吴海洋徐耀东张黎明张文娟
张 凯,吴海洋,徐耀东,张黎明,张文娟,姚 军
(1.中国石油大学石油工程学院,山东青岛266580;2.胜利油田勘探开发研究院,山东东营257015)
考虑地质及开发因素约束的三角形井网优化
张 凯1,吴海洋1,徐耀东2,张黎明1,张文娟1,姚 军1
(1.中国石油大学石油工程学院,山东青岛266580;2.胜利油田勘探开发研究院,山东东营257015)
在油气田开发中,影响原油采收率的因素有多种,除了油藏自身的渗透率场分布以及边界、断层、裂缝等地质因素外,还要考虑原始井位约束、布井方式、井网单元结构、注采量等开发因素的影响。在借鉴网格剖分理论中的Delaunay三角网格剖分及Voronoi图的基础上,改进Delaunay三角网格剖分只能约束采油井的局限性,使之还能约束注水井,实现在断层、生产井和注水井等约束条件下的三角形井网构建,并使用最优化方法中的PSO算法实现矢量井网的优化。结果表明,井网可以根据地质情况与油水的不同分布,以及各井网单元的尺度、方位,实现变尺度、变密度的井网布局优化。同时,考虑单元内渗透率的各向异性,通过调节注水井的井位可以实现更好的均匀驱替效果。
三角形井网;矢量井网;粒子群优化算法;井网优化
井网的设计在油田开发过程中具有十分重要的作用。目前,许多研究人员在井网优化方面做了较多工作:解析方法是把井网优化问题转化为单一参数“井网密度”优化问题设计井网[1-2];随着科技知识的发展,更多的学者采用数值模拟研究井网优化问题[3-6];优化理论在石油行业也有多方面的应用[7-10]。笔者提出考虑地质及开发因素约束的三角形井网优化方法,旨在解决井网如何与目前的开发动态和已有的井网的匹配问题,通过建立数学模型,实现约束求解,给出考虑多种因数约束下的最优井网形式。
1 考虑地质因素以及开发因素约束的井网
1.1 传统矢量井网定义
矢量井网优化是一种考虑油藏非均质情况进行井网设计的典型方法。它是目前一种能够解决非均质井网单元布井问题的方法,根据地质条件不同,能够给出单元内不同的井距,实现整个单元均匀驱替,矢量井网即在此种情况下被提出。刘德华[11]等介绍了矢量井网的相关概念,并定性描述了井网部署方法。所谓矢量井网,是以沉积的物源方向、河流走向或主渗透率方向为基础部署的阈值相适应的井网,同时考虑油层分布、裂缝方向、沉积微相的一种综合布井方式。开发井网也可称之为矢量井网,是由于井排之间水驱具有一定的方向性,若井网矢量与地质矢量一致,则油田能获得较好的经济效益。李阳[12]等人在研究矢量井网的时候指出,要实现一个注采单元的均衡驱替,各向异性介质油藏不同方向上的井距必须满足如下关系:

式中,dx为x轴方向上生产井与注水井间距;dy为y轴方向上生产井与注水井间距;Kx为x轴方向上的渗透率;Ky为y轴方向上的渗透率。
式(1)表明,为了实现一个注采单元的均衡驱替,注水井到周围生产井的距离的比值应等于各个方向的渗透率的0.5次方的比值,以此为依据进行井网的调整。
1.2 考虑地质因素以及开发因素约束的井网
针对矢量井网问题,考虑油田的实际情况,提出了一种同时考虑地质因素以及开发因素约束的三角形井网优化的方法。这种方法能够根据实际油田约束条件的变化实现变尺度、井网单元方向可调等多种功能。在油田生成井网时,不仅考虑到油藏边界、油藏内部断层、裂缝等地质因素的影响,还考虑了开发因素的影响,例如对于已经有少量井的油田,实现井网加密时还会遇到生产井和注水井的约束。
在实际的油田开发工作中,不同类型的油田天然能量的大小以及天然能量的类型有所不同,油田的规模各异,开发者对油田产量的要求会随着外部条件而做出调整,油田的开采特征和开采方式也各有不同,所以在井网生成过程中遇到的更多的问题是一个区块中的生产井的约束问题。在进行井网加密的过程中,原有的生产井位置已经确定,新生成的井网必须在原有的生产井的基础上构建。
本文中所定义的矢量井网是考虑了现有的油水井井网布局,以及油藏内外的断层及尖灭的无油区等边界和自身物性的特点,根据油藏不同的沉积相分布,生成最优井网加密形式、最优变尺度单元、最优尺度、最优井数、最优注采关系并考虑了边界的一套井网。定义的矢量井网具有以下特征:
(1)尺度可变。如图1所示,油藏本身地质特征复杂多变,渗透率场以及油水的分布情况也是随着开发在不断变化的,因此井网单元的尺度需要及时进行调整,已达到最佳的开发效果。由六边形井网单元ABCDEF缩小变化为A*B*C*D*E*F*。
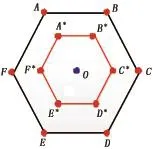
图1 尺度不同Fig.1 Different scale
(2)具有方向性。如图2所示,随着油田开发进程的不断推进,油藏的驱替会导致油水的重新分布,渗透率场也在随时更新,这个时候井网单元要做出适时的调整方位,使得驱替向着更有力的方向进行。由六边形井网单元ABCDEF旋转45°变化为A*B*C*D*E*F*。

图2 方向不同Fig.2 Different direction
(3)区域单元不同尺度不同。如图3所示,在实际油田布井过程中,区域中往往会有各种各样的限制条件,如已有井位、断层、裂缝等,所以布井时要据此对单元进行调整,各个单元的大小、方向会有所不同。如图中左下角六边形单元相比较于右上角要稀疏、尺度要大一些。

图3 区域不同单元尺度不同Fig.3 Different area and unit scale
(4)具有边界、断层、原始井位约束。如图4所示,对于已开发的成熟油田来说,已广泛布置了探井或已开发的油水井,这些油水井呈散点分布,因此新生成的井网要求涵盖已有油水井,新井网的井点必须与已存在的油水井井点完全重合;对于油藏本身,除了油藏边界外,其内部往往存在有断层、尖灭无油区,因此要求新井网需与油藏内外边界等条件相契合。
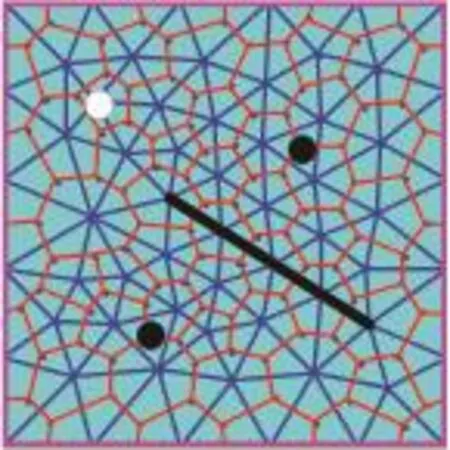
图4 边界、断层、原始井位约束Fig.4 Constraint of boundary,fault and initial well location
2 井网优化问题
2.1 井网优化背景
对于上述提出的矢量井网,如何对其进行优化,使之适应不同的实际油藏是需要考虑的问题。由于地质条件的各向异性,在注水开发时水相容易沿着高渗通道率先突破至生产井底,造成水窜,导致生产井之间见水时间出现差别,而且随着高渗通道的阻力的减少,舌进现象会越来越严重,对开发有着很不利的影响。
此外,对于均质油藏来说,井网对采收率的影响不明显。但是,对于非均质油藏,尤其是岩性复杂或不连续的油藏,井网对采收率有相当大的影响,特别是在油田开发后期,井网的形态与井网密度对开发效果起着决定性的作用。在井网形态不变的前提下,井网密度越大,最终采收率就越高,但考虑到井数的增多会大幅增加投资的成本,因此并不是井数越多油田经济效益越好,而要找到一个最优的平衡点,既要增加产出,又要降低投入。所以,如何对井网进行合理的优化,设计出最优的井网形式,对于经营者来说是十分重要的。
2.2 模型构建
对于自适应井网的构建问题,首先运用平面二维Delaunay三角网格生成原理,并在此基础上考虑油藏边界、油藏内部断层、初始生产井以及注水井井位的限制,由此得到油田井网生成器,然后将井网生成器与井网优化程序相链接。给定油田边界、断层、初始生产井、注水井井位以及初始井网密度,在给定约束条件下生成一套初始井网,然后利用井网优化程序调用商业数值模拟软件计算初始井网的净现值(net present value,NPV)。选择初始边界点和生产井、注水井的井网密度以及油田总注采量作为优化变量,使用PSO算法改变各个优化变量的值得到井网生成器的输入文件。井网生成器利用新的输入文件重新生成另一套新的井网。井网优化程序再次调用油藏模拟软件计算净现值。重复此步骤直到净现值取得最大值,直至得到最优井网。
2.2.1 目标函数
从工程的角度上来讲,对一个油田的开发总希望能尽可能多地采出储层中的原油,以提高油田的原油采收率,因此累积采油量自然成为油田各个参数优化的目标函数。从油藏经营管理的角度上来讲,管理者追求的目标是获得最大的经济采收率,所以应该正确合理地应用各种资源进行油气田的开发。对资源的要求和利用,应该把长期开发、持续开发贯穿于整个油田的开发进程中,以最佳经济效益作为为核心,因此把油田的净现值(VNP)作为优化的目标函数从经济的角度来说更具合理性。本次优化过程将以油田的净现值VNP作为目标函数。
净现值是一项投资所产生的未来现金流的折现值与项目投资成本之间的差值。一般说来,净现值大于零则方案可行,且净现值越大,方案越优,投资效益越好,而净现值为负值则投资方案是不可以接受的(不考虑其他如公司的战略性决策等因素)。在净现值均大于零的情况下,净现值最大者为最优方案。其计算公式为

用符号表示为
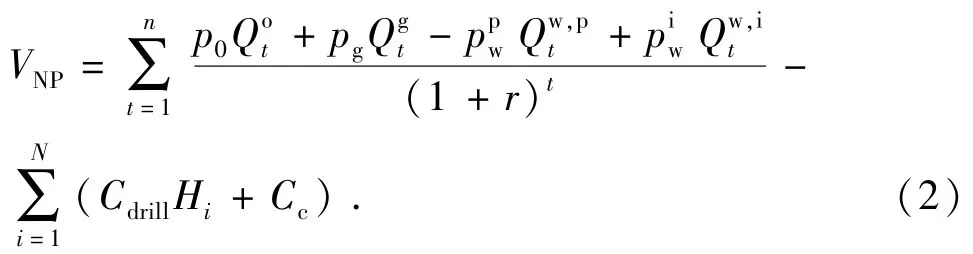
式中,VNP为净现值,元;r为贴现率;n为投资项目的寿命周期,a;N为总井数;Cdrill为平均单位长度的钻进成本,元/m;Hi为第i口井井深,m;Cc为完井成本,元/口;po为原油的销售价格,元/t;pg为天然气的销售价格,元/m3为第t年的原油销售量为第t年的天然气销售量为单位采水费用,元/t为单位注水费用,元/t;为第t年采出的水量为第t年注入的水量,t。
为了便于计算和分析,假设原油和天然气的销售价格、单位注水和采水费用均为常数,在实际运用中用户可以根据需要自行调整。
使用改进的网格生成器进行井网的自动生成时,区块的边界以及初始生产井和注水井的位置均已固定,唯一可以改变的是初始点集的密度控制值,当改变个点的密度控制值时生成的井网也将发生变化,井的数量和井的位置都将改变。本文中把各个初始点的密度控制值以及整个油田的注采量取为优化变量。设初始点有n个,则优化变量为(n+1)个。优化的目的就是寻找各点合适的密度控制值以及全油田的注采量,使得生成的井网在该注采量下能取得最大净现值。
2.2.2 优化变量
井网中存在大量的井位,如果仅优化井的位置,很难保证各井网的点相互不交叉,这使得井位优化的方法不能应用于井网优化。为了解决井位离散优化的问题,设定优化的变量为油藏内不同位置处三角形单元的边长。根据Delaunay理论的特性,如果设定该点单元的边长,周围单元的边长将参照其长度进行调节,也就是说:如果设定单元边长短,该位置处井网单元的密度就大;边长长则单元的密度就小。优化变量的个数取决于选取点的个数,通过对这些点的优化,可以间接优化油藏中不同位置井网的密度,实现规模化、变尺度、变密度的井网布局。单元设定边长的大小需要考虑油藏的长、宽,一般最大值不超过油藏长、宽最短距离的一半。优化的过程中,设置的点如图5所示,包括:
(1)外边界上的点。如图中红色的点。
(2)内边界上的点。如图中黑色的点。
(3)断层上的点。如图中黄色的点。
(4)注采井点。如图中粉色的点为采油井位,绿色的点为注水井位。
(5)其他点。如图中蓝色的点代表没有受井网控制的点的位置。
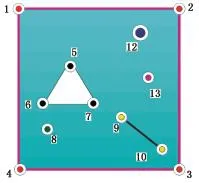
图5 设置点的位置Fig.5 Location of points set
3 井网生成及优化求解
基于Delaunay三角网格剖分的理论和Voronoi网格生成理论生成考虑约束条件的井网,并在此基础上利用PSO方法对井网进行优化,得到最优的井网布局。
3.1 Voronoi网格生成和Delaunay三角网格剖分
3.1.1 常规的Voronoi及Delaunay网格
设定油藏的外边界、内部的断层和尖灭区及井点的坐标位置,如图6所示。输入文件包含有点的信息和边的信息两部分。其中点的信息有点的数量、坐标、密度控制值、标记值等;边的信息有起始点、终止点、各边的标记等。
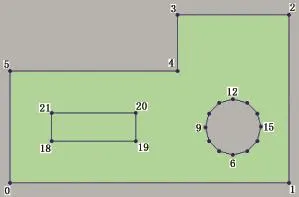
图6 初始区域Fig.6 Initial area
构造一个足够大的三角形,包含整个需要布井的油藏区域。首先生成初始边界剖分,根据设定的初始条件,由两个端点处的单元边长的大小插入散点,构建三角形。将点集中的散点依次插入,形成一个初始的Delaunay三角网格剖分。将位于剖分区域外部的三角形删除,得到区域内部的初始三角剖分,直到所有的三角形都满足要求或总点数大于最大点数,最终完成Delaunay三角剖分,把该区域的Delaunay三角剖分与其对偶图Voronoi叠加在一起后结果如图7所示。

图7 Delaunay三角剖分和Voronoi图Fig.7 Delaunay triangulation and Voronoi diagram
3.1.2 Voronoi网格约束点算法的改进
由于借鉴的网格生成程序在进行网格剖分时完全没有考虑最终生成的Delaunay三角网格的对偶图Voronoi图,只进行区域的三角剖分,区域的Delaunay三角剖分完成以后,Voronoi图自然得以确定,因此当一个区域存在Voronoi图的顶点约束时,由于网格生成器没有处理Voronoi图的模块,无法生成用户想要的网格。也就是说,当存在生产井时,原有的网格生成程序无法进行井网的自动生成,需要对算法约束进行改进。
本文中对网格剖分程序改进如下:首先根据输入文件计算每一口生产井的最大空圆,如果某一口生产井的最大空圆上只有一口或两口注水井,则主动在该生产井的最大空圆上添加两口或一口注水井,使每一口生产井的最大空圆上都有3口或3口以上的注水井。添加的准则是使添加后得到三口注水井形成的三角形尽量接近等边三角形。为了确保在随后的区域三角剖分中不会有新的点插入到各口生产井的最大空圆内部,将各口生产井的最大空圆上的注水井的密度控制值设置为空圆上的注水井沿着顺时针或逆时针方向形成的多边形的最小边长。当输入文件中给定生产井的密度控制值时,同样首先逐口计算生产井的最大空圆,若该空圆的半径小于生产井的密度控制值的某一个倍数,则按照上述算法处理,否则说明该生产井周围的井密度过于稀疏,井距大于用户要求的井距,则人为指定该生产井的“最大空圆”半径为其密度控制值的一个合适的倍数。如图8所示实现了注采井点的约束。

图8 注采井点约束Fig.8 Constraint of injection-production point
3.2 PSO算法对井网优化求解
3.2.1 PSO算法
PSO算法被提出的初衷是为了用图形描述鸟类群体的运动情况。经过大量的观察与调查发现,鸟群中对于信息的传递与利用为演化提供了一个参考,通过考虑与其相邻个体的速度的影响,以及多方向搜索和距离的加速,提出了PSO算法[13]。后来研究者发现,在其中引入一个惯性加速度可以更好地进行开发和搜索,得到的结果更优,逐渐演变成现在较为固定的版本。
PSO算法即粒子群优化算法,顾名思义该算法是以群体为基础设计的。在该算法中群体中的个体根据环境的变化在区域中移动进行搜索,在移动过程中寻找最优的位置。该算法将每个个体看作是N维搜索空间中粒子(忽略其质量和体积,类似于物理学中的质点)。现在考虑一个由m(m也称为群体规模)个粒子构成的群体,粒子在搜索空间中按照自己的速度飞行,该速度会根据具体情况作出适时的动态调整。其中第i个微粒的初始位置表示为Xi=(xi1,xi2,…,xin),粒子迄今为止搜索到的最优位置表示为Pi=(pi1,pi2,…,pin),也称为pbest。在群体所有微粒经历过的最优位置的索引号用符号g表示,即Pg,也称为gbest。微粒i的速度用Vi=(vi1,vi2,…,vin)表示。
对每一次迭代,微粒i的第n维(1≤n≤N)速度更新由下式确定:

式中,w为惯性权重(inertia weight);c1和c2为学习因子(acceleration constants),也称为加速因子;rand()和Rand()为两个在[0,1]范围里变化的随机值;k为迭代次数。
粒子更新后的位置变化由下式表示:

另外,任意一个微粒的某维速度Vi不能超过设定的最大速度Vmax。如果某一微粒在其某维的速度Vid大于最大速度Vmax,则把最大速度赋值给该速度。
PSO算法的流程图如图9所示。

图9 PSO算法流程图Fig.9 Flow chart of PSO algorithm
3.2.2 井网优化求解过程
本文中将井网生成与井网优化相结合后,给定初始基本参数,便可自动进行优化,最终生成一套最优的井网,其具体优化步骤如下:
(1)首先建立油藏模型,给定油藏数值模拟所需要的各类参数,包括储层面积、储层厚度、储层物性参数,如孔隙度分布、相对渗透率曲线以及生产动态等资料。此外,还需要给定井网生成和井网优化所需要的一些数据,如油田已有的生产井和注水井的井位等信息,以及优化井网时的迭代步数、油气水的价格等参数。
(2)给定油藏的基本参数并建立起油藏数值模型后,井网生成器会根据初始条件如油田的边界点、已有的生产井和注水井的井位以及设定参数生成一套初始井网。
(3)将生成的初始井网中各井的井位与油藏模拟器进行网格匹配,通过油藏数值模拟获得油田开发指标。利用油田开发指标计算总的净现值,即初始井网的净现值。
(4)由于目标函数和优化变量之间没有显式的函数关系式,利用PSO算法实现井网的优化,每一次迭代完之后进行下一次的搜索,直到达到最优或者达到最大迭代步数。
(5)经过多次迭代之后得到目标函数的最优值。每计算一次目标函数的值及净现值时都需要将各个优化变量的值传递给井网生成器生成一套井网。当目标函数取得最大值时的井网即为所需要的最优井网。
4 实例分析
本文中选取一个2维非均质油藏,油藏初始含油和水,油藏原始压力30 MPa,生产井定液量生产,油藏的总注入量保持不变,注采比为1∶1,模拟总生产时间为10 a。每口注水井和生产井的成本估计为5× 106元,原油的价格为3000元/t,处理产出水的费用为100元/t,注入水的费用为100元/t。统一对含水率小于50%的层位射孔。油藏假定为确定模型。

图10 初始约束条件Fig.10 Initializing constraint
选取油田净现值为目标函数,应用PSO优化程序分析井位优化问题,本实例中使用了常用的商业油藏模拟器。在建立的地质模型中将该区块看作边界规则的二维油藏,网格划分为50×50,网格大小为50 m×50 m×10 m。在初始条件下,定义油田含有2口生产井和1口注水井以及一条不渗透边界,用井网生成器所生成的井网中必须保证这3口已有的井和断层的位置不变,其初始位置以及渗透率场如图10所示。从该区块的初始渗透率场分布图可以看出,该油藏含有3条高渗通道,其中绿色的点代表初始的注水井位,两个红色的点代表的是初始的生产井位,红色的线代表的是断层位置。
初始井网和最终优化后井网如图11、图12所示。
对比井网形式,可以看出在高渗透带周围的注水井减少,避免了水沿着高渗透带突进,在低渗带优化显著,由原先的密集转为优化后的稀疏,节省了生产成本;在断层上布置的都是假想的注水井,而且对比原始井网和最终优化后的井网发现,断层附近的井网单元有所减少,使得开发向着更有利于采出更多的油的方向发展。综合图13和图14分析可以看出,在断层下方的含水分布多于上方,但是井网要密于下方,这一方面是出于对渗透率的不同考虑,另一方面考虑的是驱油效果,在断层下方低渗带加强注水可以防止油过多地集中在断层附近采不出来而形成死油区,造成浪费。另外,观察3口初始井位可以看出在注水口井附近优化井网单元由大变小、由疏变密,而在生产井附近则相反,井网单元由小变大、由密变疏,下方的生产井变化尤为明显,是基于渗透率和断层等影响因素考虑的结果。

图11 初始井网Fig.11 Initial well pattern
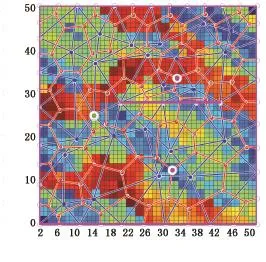
图12 最终优化后的井网Fig.12 Well pattern after final optimization
如图13和图14所示,原始井网的饱和度分布含水大多集中在高渗透带,而优化后的井网含水分布多向低渗透带分布,在低渗透带加强注采,增大了低渗透带的含水分布,防止了注水开发时水相沿着高渗透带的水窜,增加了低渗区域的采油量,从而提高了注水开发的效率。在断层附近注水明显增多,以便于采出附近的原油,避免在断层附近形成死油区造成原油无法采出。
如图15所示,随着含水率的上升累产油量逐渐增加,而且优化后的累产油量较之优化前有大幅度的提升,对比两次优化的结果,最终优化后井网的累产油也有所增加。虽然井网稀疏,井的数量大量减少,但是采出的油却增多,因此该优化方法对于实际油田开发具有可行性。采出的原油增多,一方面原因是由于在高渗透带含水下降,避免了不必要的浪费,提高了注水波及范围;另一方面,在断层附近注水明显增多,把断层附近原先井网不能采出的油开采出来,使产油量得到了提高。

图13 原始井网的饱和度分布Fig.13 Saturation distribution of initial well pattern
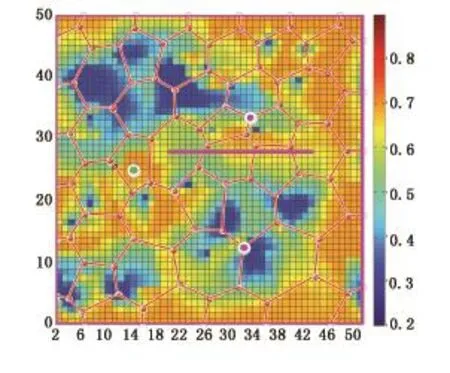
图14 最终优化后饱和度分布Fig.14 Saturation distribution of final optimization
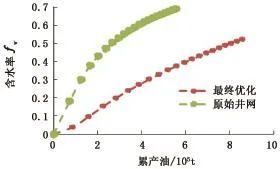
图15 累产油和含水率的关系曲线Fig.15 Curves between cumulative oil production with water cut
如图16所示,随着迭代次数的增加VNP的值呈增长的趋势。利用PSO算法进行搜索时需要对每个随机初始化粒子的井网密度进行3个梯度方向的叠加,每个粒子会搜索到一个最优的井网密度,比较所有粒子得到群体中最优的井网密度值,由此计算得到本次迭代最优的VNP值,然后进行下一次迭代。在迭代过程中调整搜索方向要受到3个梯度方向的约束,调整较为缓慢,因此会有一段时间的近乎停止增长,但是在调整到适合的方向时VNP会有较明显的增长。

图16 净现值随迭代次数的变化曲线Fig.16 Curve of net present value with iteration
5 结 论
(1)借鉴网格剖分理论中的Delaunay三角网格剖分,通过对其进行改进,实现了在考虑断层、边界及已有注采井等复杂情况约束下的三角形井网生成。
(2)通过将井网生成理论与最优化方法相结合,实现了考虑约束条件下的井网优化,通过迭代计算,能够依据现有的地质条件与开发状况,生成与之相适应的最佳井网匹配形式。
(3)利用理论测试实例,证明了该方法的正确性,能够用于复杂情况下油田三角形井网的构建与优化;但是,目前此项理论仅适用于三角形井网,对于矩形井网来说,难以考虑具体的约束条件,有待进一步深入研究。
[1] 邴绍献,李志学,王兴科,等.基于储量价值的油田井网密度优化模型及其应用[J].西安石油大学学报:自然科学版,2008,23(6):46-50. BING Shaoxian,LI Zhixue,WANG Xingke,et al.Model for the optimization of oilfield well network density based on petroleum reserves value and its application[J].Journal of Xi'an Shiyou University(Natural Science Edition),2008,23(6):46-50.
[2] LIU N,JALALIi Y.Closing the loop between reservoir modeling and well placement and positioning[R].SPE 98198,2006.
[3] BANGERTH W,KLIE H,WHEELER M F,et al.On optimization algorithms for the reservoir oil well placement problem[J].Computational Geosciences,2006,10(3):303-319.
[4] 张凯,姚军,刘顺,等.埕岛油田6A+B区块油藏动态优化方法研究[J].中国石油大学学报:自然科学版,2009,33(6):71-76. ZHANG Kai,YAO Jun,LIU Shun,et al.Reservoir dynamic control in block 6A+B of Chengdao Oilfield[J]. Journal of China University of Petroleum(Edition of Natural Science),2009,33(6):71-76.
[5] GUYAGULER B,HORNE R N.Uncertainty assessment of well placement optimization[R].SPE 71625,2001.
[6] NORRENA K P,DEUTSCH C C.Automatic determination of well placement subject to geostatistical and economic constraints[R].SPE 78996,2002.
[7] 姚军,魏绍蕾,张凯,等.考虑约束条件的油藏生产优化[J].中国石油大学学报:自然科学版,2012,36(2):125-129. YAO Jun,WEI Shaolei,ZHANG Kai,et al.Constraint reservoir production optimization[J].Journal of China U-niversity of Petroleum(Edition of Natural Science),2012,36(2):125-129.
[8] MONTES G,REPSOL F,BARTOLOME P,et al.The use of genetic agorithm and quality map[J].SPE Latin America&Caribbean Petroleum Engineering Conference,2001,5:1-10.
[9] BECKNER B L,SONG X.Field Development planning using simulated annealing—optimal economic well scheduling and placement[R].SPE 30650,1995.
[10] ZHANG K,LI G M,ALBERT C,et al.Optimal well placement using an adjoint gradient[J].Journal of Petroleum Science and Engineering,2010,73(3/4):220-226.
[11] 刘德华,李士伦,吴军.矢量化井网的概念及布井方法初探[J].石油天然气学报,2004,26(4):110-111. LIU Dehua,LI Shilun,WU Jun.Concept of vector well pattern and method of well pattern arrangement[J]. Journal of Jianghan Petroleum Institute,2004,26(4):110-111.
[12] 李阳,王端平,李传亮.各向异性油藏的矢量井网[J].石油勘探与开发,2006,33(2):225-227. LI Yang,WANG Duanping,LI Chuanliang.Vectorial well arrangement in anisotropic reservoirs[J].Petroleum Exploration and Development,2006,33(2):225-227.
[13] 张千里,李星.基于粒子群优化算法的模糊模拟[J].计算机工程,2006,32(21):33-34. ZHANG Qianli,LI Xing.Fuzzy simulation based on particle swarm optimization algorithm[J].Computer Engineering,2006,32(21):33-34.
(编辑 修荣荣)
Triangulated well pattern optimization constrained by geological and production factors
ZHANG Kai1,WU Haiyang1,XU Yaodong2,ZHANG Liming1,ZHANG Wenjuan1,YAO Jun1
(1.College of Petroleum Engineering in China Petroleum University,Qingdao 266580,China;2.Shengli Oilfield Institute of Geological Sciences,Dongying 257015,China)
In the process of oil and gas field development,a variety of factors can have a great effect on oil recovery.Apart from the geological factors such as permeability distribution,reservoir boundaries,faults and fractures,the production factors,such as the constraints of well location and spacing,well structure and the balance of injection and production are also very important to oil recovery.In this paper,based on the theory of Delaunay and the Voronoi graph,an improved Delaunay triangulation method was used,in which a triangulated well pattern can be constructed under the constraints of fault,production and injection wells to restrain not only injection wells but also production wells.In using an optimization method of PSO,vector well pattern can be further optimized.Well pattern can be adjusted according to the geological conditions and the distribution of oil and water,in terms of unit pattern size and well orientation,to achieve better well pattern optimization.Meanwhile,in consideration of permeability anisotropy,adjusting the locations of injection wells can obtain better oil recovery effect.
triangle well pattern;vector well pattern;particle swarm optimization;well pattern optimization
TE 324
A
1673-5005(2015)04-0111-08
10.3969/j.issn.1673-5005.2015.04.015
2015-01-20
国家科技重大专项(2011ZX05024-002-008,2011ZX05005-006-005);国家自然科学基金项目(61104170,61004095);国家“863”重大项目(2013AA09A215);长江学者和创新团队(IRT1294)
张凯(1980-),男,副教授,博士,从事油气田开发研究。E-mail:reservoirs@163.com。
引用格式:张凯,吴海洋,徐耀东,等.考虑地质及开发因素约束的三角形井网优化[J].中国石油大学学报:自然科学版,2015,39(4):111-118.
ZHANG Kai,WU Haiyang,XU Yaodong,et al.Triangulated well pattern optimation constrained by geological and production factors[J].Journal of China University of Petroleum(Edition of Natural Science),2015,39(4):111-118.
