裂缝充填物对脉动水力压裂应力扰动效果的数值模拟

陆沛青，李根生，沈忠厚，黄中伟，盛 茂，迟焕鹏

（中国石油大学油气资源与探测国家重点实验室，北京102249）

裂缝充填物对脉动水力压裂应力扰动效果的数值模拟

陆沛青，李根生，沈忠厚，黄中伟，盛 茂，迟焕鹏

（中国石油大学油气资源与探测国家重点实验室，北京102249）

利用线性滑移模型、有限差分及交错网格技术研究脉动水力压裂过程中应力在含裂缝地层中的传播与分布规律，分析不同缝间距和震源频率下裂缝充填物对脉动水力压裂应力扰动效果的影响机制。结果表明：含矿物质裂缝对脉动水力压裂应力扰动影响微弱，可近似看作均质区域；含液体裂缝可通过反射作用引起强透射区与弱透射区介质速度的差异，引发剪应力形成拉伸破坏，但当距离震源较近时，反射波易抵消压力波，削弱压裂效果；含气体裂缝类似含液体裂缝，但反射作用更强烈，距离震源更远才能提升压裂效果；脉动水力压裂可利用裂缝的非均质性促进压裂效果，缝间距为初始人造裂缝长度的2～3倍时可获得较好的压裂效果。

脉动水力压裂；线性滑移模型；裂缝充填物；应力扰动效果；最优间距

由于煤层气特殊的解析与运移机制，煤层压裂的主要内容不再是控制缝长、缝高、缝宽以形成足够的单长缝，而是产生大范围的致密裂缝网络以“切割”煤层，完成体积改造［1］。将压裂液以脉动形式泵入煤层，形成大范围卸压增透区的脉动水力压裂技术为低渗煤层体积改造提供了一种新思路，该技术在国内已进行了初步的室内及工业试验［2-4］，取得了较好的应用效果，李全贵等［5］在试验基础上提出了“双频-双压”压裂工艺，朱红青等［6］利用FLAC3D研究了脉动水力压裂下裂纹尖端水压变化趋势及裂纹扩展规律。但当前的研究对象多为均质煤体，对含裂缝非均质地层研究较少。针对以上问题，笔者采用数值模拟方法研究脉动水力压裂过程中应力在含裂缝地层的传播与分布规律，分析天然裂缝充填物对煤层脉动水力压裂应力扰动效果的影响机制。

1 数学模型

1.1 基本假设

假设：①除天然裂缝，其余区域为各向同性弹性介质；②平面应变状态；③煤层孔眼直径及由射孔产生的预置裂缝相对于几十至上百米的计算域尺寸很小，可忽略沿程的应力差异，简化为相位相同的线震源；④脉动水力压裂引起的强应力扰动可使煤岩在机械强度较低处形成微裂缝、增大渗透率，但不破坏煤岩整体结构，即煤岩破损后依然按连续介质处理。

1.2 线性滑移模型

在连续性假设前提下，可采用交错网格有限差分技术模拟地层应力响应［7-8］，但须采用特殊的手段处理裂缝。目前有两种方法：一种是将包含裂缝界面的网格单元用等效介质代替，如Hundson模型［9］、线性滑移模型［10-12］、Kachanov模型［13］等；另一种是用一个充满填充物的薄层代替裂缝［14］。综合考虑计算精度与效率［15］，本文中采用较直观的线性滑移模型表征天然裂缝。

线性滑移模型假设裂缝是一个零厚度的薄层界面，跨越界面的位移/速度存在突变，而缝面上的应力连续，且同突变位移/速度增量呈线性关系［10］。当单条裂缝走向与网格坐标轴之一一致（本文中假设与x轴一致）时，线性滑移模型精确表达式［12］为

式中，Δvx为跨越裂缝沿x方向速度突变量，m/s； Δvy为跨越裂缝沿y方向速度突变量，m/s；ZT和ZN分别为屈服度张量切向分量和法向分量；ux和uy为位移分量，m；σxx和σyy为正应力分量，MPa；σxy为切应力分量，MPa。

由此可得滑移裂缝处速度-应力方程组为

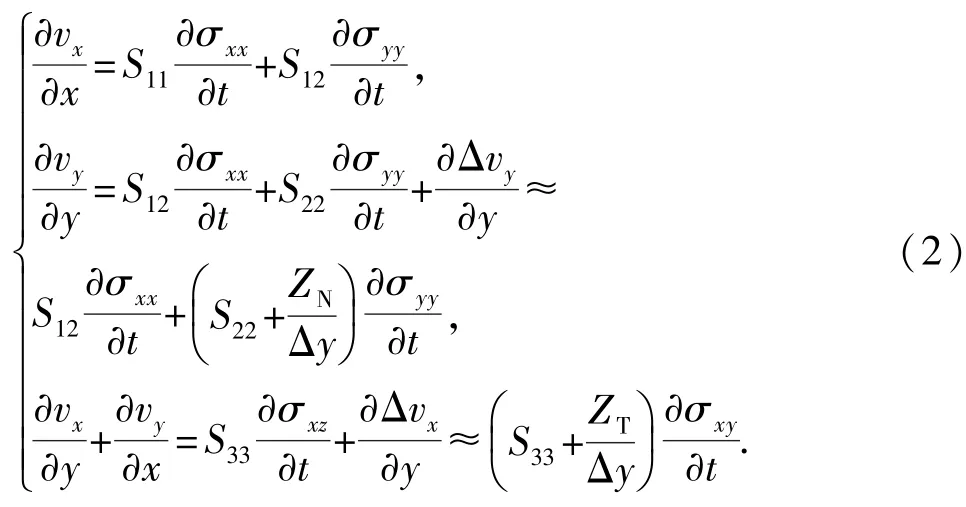
将式（2）系数矩阵求逆，可得滑移裂缝处刚度矩阵为

其中

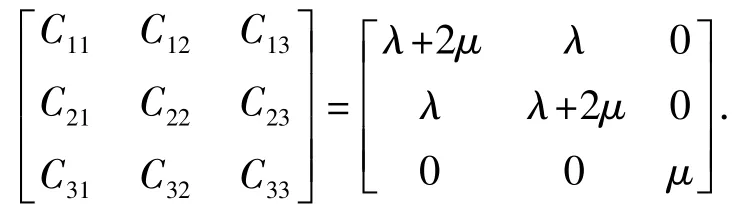
式中，Sij为背景介质柔度系数；Cij为背景介质刚度系数。

因此，有

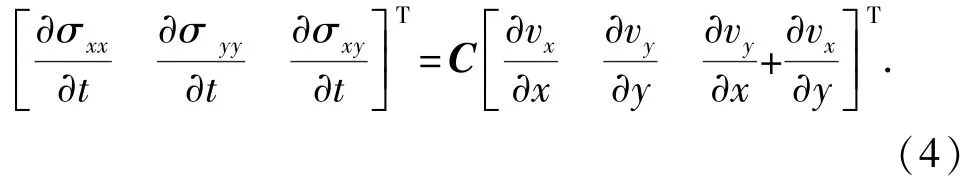
式中，λ和μ为第一、第二拉梅常数，分别表征了煤岩的压缩性和剪切模量，可通过煤岩横纵波速度计算得到，MPa。

式（4）即为滑移裂缝区域的本构方程，而针对非滑移裂缝区域，只需将ZT和ZN取0，即转换为均质介质的本构方程。

1.3 边界条件

裂缝处的线性滑移本构方程本质上属于内边界条件，本小节讨论外边界条件，即含围压无限大地层的实现。首先，采用理论上可吸收来自各方向、各频率的完全匹配层边界技术（Perfect Matched layer，PML）［16］模拟无限大地层。其基本思想是在控制方程中加入衰减系数（图1左图），压力波由计算域传到边界层后按指数规律衰减，不产生反射，表征无限大地层［17］。另一方面，须考虑地层围压的影响。利用弹性力学叠加原理设置完全相同的计算域而在边界加载围压，再将计算出的应力值同PML边界条件下得到的应力叠加，即可得到含围压无限大地层地应力分布（图1）。由于交错网格是一种初值为0的动网格模型，而围压是一种静载，因此围压应从0开始缓慢加载，直接赋值或加载过快都将产生虚假的应力震荡而使模拟失真。

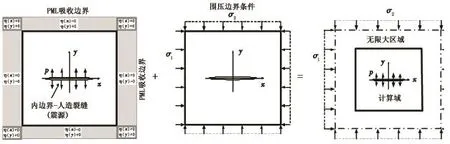
图1 含围压无限大地层边界条件加载示意图Fig.1 Boundary conditions schematic of infinite formation with confining pressure

1.4 交错网格差分实现方法

采用交错网格差分方法对波动方程进行降阶处理，将波动方程中位移对时间和空间的二阶导数降为速度和应力对时间的一阶导数，并将速度v和应力σ分别定义于两套不同的交错网格系统上进行迭代计算［9］，含裂缝地层的应力传播控制方程为

基于以上方程组，采取空间4阶，时间2阶差分精度的离散格式进行计算，具体的差分格式与文献［18］类似，只是系数不同。

采用PML吸收边界与准静态围压加载两种边界条件的均质数值模型，其动静态响应的可靠性已在文献［18］中得到验证；作为内边界条件的线性滑移模型，其对于连续介质范畴下的计算精度也已得到验证［10-12］。鉴于本文数值模型是以上两种边界条件的结合，可认为模型具有足够的可靠性与准确性。

2 模拟结果分析

图2 数值模型示意图Fig.2 Schematic of numerical model

计算域尺寸40 m×40 m，计算步长Δx=Δy=0.2 m，初始人造裂缝长4 m，天然裂缝长10 m且平行于人造裂缝，两者距离取3～15 m。震源输出半周期正弦压力波，参考目前已有脉动注水压裂设备［19-20］，频率取25～50 Hz，振幅25 MPa。地应力围压取σx=σy=5 MPa（图2）。数值模拟中的煤岩物性：密度为1500 kg/m3，纵波波速和横波波速分别为1100和500 m/s，拉梅第一常数和第二常数分别为1065和375 MPa。鉴于煤岩抗拉强度（0.25～5 MPa，本文中假设2 MPa）远小于抗压强度（5～50 MPa）［21］，因此采用最大拉应力准则作为强度判别准则，认为当煤岩所受拉应力超过煤岩抗拉强度（式（5），拉应力为负）时，将形成强应力扰动区，该区域微裂缝发育、渗透率显著提高［22］，为脉动水力压裂有效的应力扰动区。本文中采用其面积作为衡量脉动水力压裂效果的判别标准。鉴于有限差分法以节点为计算单元的特点，进一步以拉应力超过煤岩抗拉强度的节点数占总节点数的比例为有效应力扰动节点比表征有效应力扰动范围。

2.1 含矿物质裂缝

含不同填充物裂缝线性滑移示意图如图3所示。矿物质同水或空气相比刚度较高，缝间空隙较小，应力波作用时，跨越裂缝的质点位移在正应力方向与切应力方向仅产生微小的线性滑移（图3（a）），可取ZN=ZT=0.1［12］。

频率44 Hz时含矿物质裂缝地层的有效应力扰动区形状如图4所示。

由图4可知，脉动水力压裂在均质及含裂缝地层都形成了大范围的有效应力扰动区。鉴于震源输出的是压力波，人造裂缝（除端部外）附近大部分区域的节点正应力为压力（σxx>0、σyy>0），根据式（5）可知，造成节点主应力超过煤岩抗拉强度的主要因素是质点所承受的剪应力，且频率越高产生的剪应力越大，拉伸破坏作用越明显。另一方面，含矿物质裂缝对有效应力扰动区影响微弱，图4已直观显示出，有效应力扰动区形状几乎相同，不随裂缝位置的变化而变化。

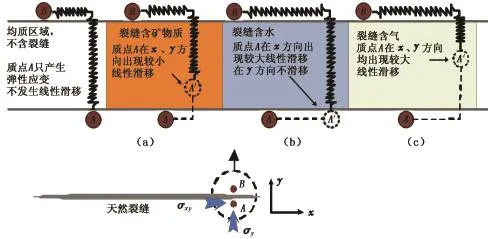
图3 含不同填充物裂缝线性滑移示意图Fig.3 Schematic of linear slip deformation in different kind of material-filled cracks

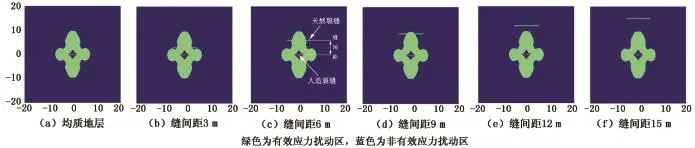
图4 脉动水力压裂频率44 Hz时含矿物质裂缝地层的有效应力扰动区形状Fig.4 Effective stress disturbance zone of mineral-filled cracked formation during PHF with frequency 44 Hz

图5为含矿物质裂缝地层有效应力扰动节点比随频率变化曲线。图5进一步表明，均质与含裂缝地层的有效应力扰动节点比变化曲线近于重合，有效应力扰动节点比差异为0.005%～0.3%。这是因为含矿物质裂缝的刚度较高，非均质性微弱，导致应力波大部分从裂缝透射而不形成反射，未引起裂缝周围强烈的速度差异，故不会产生额外的剪切应力造成拉伸破坏。

由此，对于频率低于50 Hz的脉动水力压裂，含矿物质裂缝可视为均质区域，张奇［23］从节理阻抗的角度分析也得到了与本节相似的结论。

2.2 含液体裂缝

煤层中开度较大的裂缝通常含液体，由液体的不可压缩性可认为跨越裂缝的质点在正应力方向的位移连续，而在切应力方向产生较大滑移，此时可取ZN=0，ZT=2（图3（b））。

图6为含液体裂缝地层中有效应力扰动节点比随频率变化曲线。由图6可知，含液体裂缝的存在对脉动水力压裂有效应力扰动区影响明显，不同缝间距对应力扰动效果起到截然不同作用。频率44 Hz时缝间距6 m的有效应力扰动节点比较均质地层高0.6%，缝间距9 m的有效应力扰动节点比较均质地层高0.4%；缝间距3 m时，天然裂缝则呈现明显的抑制作用，44 Hz时有效应力扰动节点比低于均质地层0.5%。缝间距12和15m的曲线同无裂缝曲线接近，但略有提升。

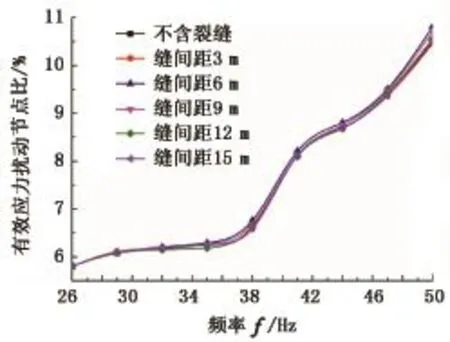
图5 含矿物质裂缝地层有效应力扰动节点比随频率的变化Fig.5 Variation of percentage of effective stress disturbance nodes with frequency in mineral-filled cracked formation

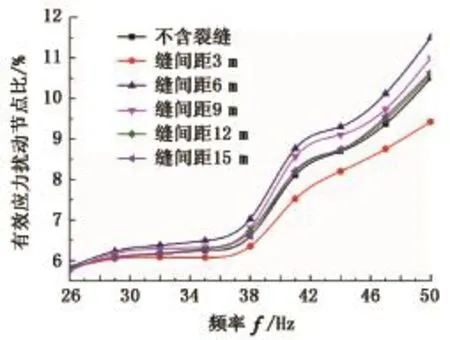
图6 含液体裂缝地层有效应力扰动节点比随频率的变化Fig.6 Variation of percentage of effective stress disturbance nodes with frequency in fluid-filled cracked formation

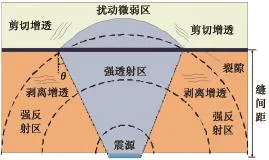
图7 裂缝处反射区与透射区示意图Fig.7 Schematic of reflection region and transmission region around crack

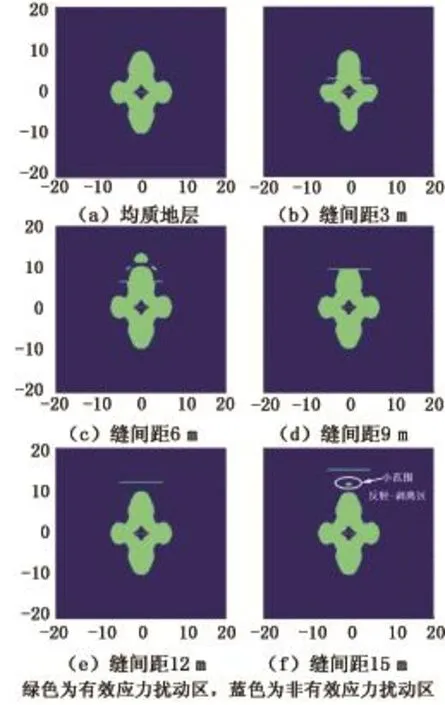
图8 脉动水力压裂频率44 Hz时含液体裂缝地层的有效应力扰动区形状Fig.8 Effective stress disturbance zone of fluid-filled cracked formation during PHF with frequency 44 Hz

分析认为，由含液体裂缝引起的反射与透射效应是造成上述差异的主要原因。液体的刚度较矿物质充填物低，ZT>1时不能忽略入射角对裂缝反射、透射系数的影响。裂缝处反射区与透射区示意图如图7所示。入射角度小于临界入射角θ时，波以透射为主，大于临界入射角θ则以反射为主。长度相同的天然裂缝距人造裂缝越近，反射作用越强、应力扰动作用越弱。

缝间距为3 m时反射效应最强，有相当比例的压力波经含液体裂缝反射形成拉伸波，但因距人造裂缝较近，拉伸波与震源产生的压力波相抵，一定程度上削弱了震源附近的应力扰动，故有效应力扰动节点比较低（图8（b））；缝间距6 m时，因距离增大，反射波已不足以削弱震源的影响，但较强的反射效应使强透射区与弱透射区形成强烈的速度差异，产生了较大范围的剪切应力，从而大幅提高有效应力扰动面积（图8（c））；缝间距为9 m时，含液体裂缝处于应力强扰动区的边缘，强透射区与弱透射区的速度差异不再明显，此时反射产生的拉伸波（σxx< 0、σyy<0）成为裂缝附近应力扰动的主导因素，缝之间的扰动面积较无裂缝时更宽（图8（d））；缝间距12～15 m时，含液体裂缝远离应力强扰动区，反射与透射效应影响较微弱，但当频率足够高时仍然会在裂缝间反射形成小范围的拉伸破坏区（图8（f）），而总体应力扰动效果与均质地层差别不大。

2.3 含气体裂缝

当应力波作用于含气体裂缝时，跨越裂缝的质点位移在正应力方向和切应力方向都会产生较大滑移，此时可取ZN=ZT=2（图3（c））。由于在跨越裂缝的正应力方向也出现了线性滑移现象，含气体裂缝的反射效应比含液体裂缝更加强烈。

图9（b）～（e）清晰地显示出有效应力扰动区在远离天然裂缝的方向较发育，而图9（f）因含气体裂缝距人工裂缝较远，直接在裂缝之间形成了大范围的反射-剥离有效应力扰动区。

图9 频率44 Hz时含气体裂缝地层的有效应力扰动区形状Fig.9 Effective stress disturbance zone of gas-filled cracked formation during PHF with frequency 44 Hz

含气体裂缝地层有效应力扰动节点比随频率变化曲线如图10所示。图10表明，当震源频率低于40 Hz时，含气体裂缝的存在遏制了脉动水力压裂的应力扰动效果（缝间距15 m除外），原因为反射产生的拉伸波一定程度上抵消了震源压力波；当频率高于40 Hz后，反射效应进一步加强，反射波的能量足以克服压力波，在含气体裂缝远端造成强烈的速度扰动，形成剪切损伤，促进了应力扰动效果，这种先削弱后增强的现象在缝间距为12 m的曲线上体现尤为明显。

由此可见，含气体裂缝对脉动水力压裂应力扰动效果的影响规律类似含液体裂缝，只是含气体裂缝的反射作用更加强烈，只有当频率足够高或距离足够远时才能提升脉动水力压裂应力扰动效果。

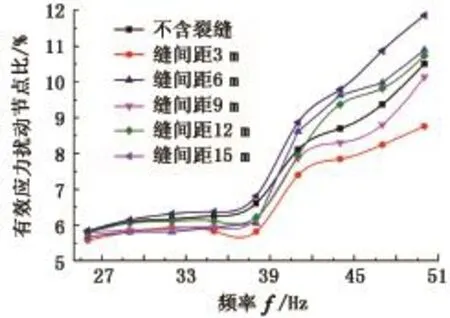
图10 含气体裂缝地层有效应力扰动节点比随频率的变化Fig.10 Variation of percentage of effective stress disturbance nodes with frequency in gas-filled cracked formation

2.4 进一步分析

Li与柴少波等［24-25］将影响天然裂缝透、反射系数的屈服张量、背景介质密度、波速及入射波频率统一地归纳为一个无量纲参数节理刚度：

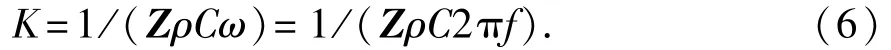
式中，Z为屈服张量；ρ为背景介质密度，kg/m3；C为背景介质波速，m/s；f为入射波频率，Hz。

由式（6）可知，在背景介质（煤岩）密度、波速及入射波频率一致的情况下，填充物屈服张量越大，无量纲节理刚度越小。较小的无量纲节理刚度意味着裂缝的透射系数减小、反射系数增大，裂缝将对应力波产生较大的干扰作用。

本文中，矿物质填充取ZN=ZT=0.1，液体填充取ZN=0、ZT=2，气体填充取ZN=ZT=2，则KN矿、KN液、KN气的比值为10∶无限大∶0.5，KT矿、KT液、KT气的比值为10∶0.5∶0.5。鉴于含矿介质对应力波的干扰几乎可以忽略，可认为K≥10后应力波能量完全穿透天然裂缝而无反射。理论上，含水裂缝正应力完全透射而切应力95%的能量将被反射；含气裂缝正应力与切应力95%的能量都被反射，从而与入射波叠加形成较强的应力扰动效果，这一现象同本文数值模拟的结果基本吻合。

2.5 最优缝间距

天然裂缝的反射与透射效应受裂缝屈服张量、裂缝与人造裂缝（震源）的间距与尺寸、震源频率、煤岩物性等多种因素影响，其中可控参数为：初始人造裂缝与天然裂缝的间距H、初始人造裂缝长度L及震源频率。取缝间距与初始人造裂缝长度的比R =H/L综合表征人造裂缝的展布方式。

为寻找最优的初始人造裂缝展布参数，分别计算天然裂缝含液体/气体时典型震源频率下有效应力扰动节点比随R的变化，结果如图11所示。

由图11可知，对于含液体裂缝，最优R值区间为［1.25-2］，即初始人造裂缝与天然裂缝的间距为其长度的1.25～2倍时可获得较好的脉动水力压裂效果；对于含气体裂缝，出现两个最优R值点，即R =1.5和R=3.75处，若取R=1.5，则有效应力扰动区主要在远离天然裂缝方向发育（图8（c）），若取R =3.75，则有效应力扰动区主要在天然裂缝与人造裂缝之间发育（图8（f））。

由此可知，人造裂缝与天然裂缝的间距为人造裂缝长度的2～3倍时，可充分利用天然裂缝的反射效应获得较好的脉动水力压裂效果。

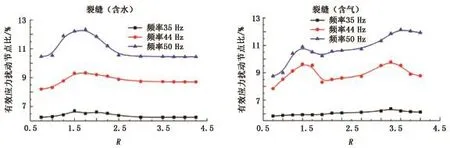
图11 不同频率下有效应力扰动节点比随R的变化Fig.11 Variation of percentage of effective stress disturbance nodes with R in different frequencies

3 结 论

（1）填充物为矿物质时裂缝刚度较高，压力波大部分从含矿物质裂缝透射而不形成反射，因此含矿物质裂缝可近似看作均质区域，对脉动水力压裂效果影响微弱。

（2）填充物为液体时裂缝刚度较低，可反射压力波形成拉伸波，产生剥离破坏，同时引起强透射区与弱透射区介质速度的强烈差异，造成剪切破坏；但当天然（含液体）裂缝与人造裂缝距离较近时，反射-拉伸波易削弱震源的影响，降低压裂效果。

（3）填充物为气体时，对脉动水力压裂应力扰动效果的影响规律类似含液体裂缝，只是含气体裂缝的反射作用更加强烈，只有当频率足够高或距离足够远时才能提升脉动水力压裂效果。

（4）脉动水力压裂技术可在一定程度克服、甚至利用煤岩的非均质性，通过分析初始人造裂缝展布方式对应力扰动效果的影响规律发现，缝间距是初始人造裂缝长度的2～3倍时可充分利用天然裂缝的反射效应获得较好的脉动水力压裂效果。

（5）本文数值模拟基于线弹性连续介质模型，但实际地层可能出现黏弹性特征，导致应力波频率越高能量衰减越剧烈。在此情况下，裂缝对脉动水力压裂应力扰动效果的影响规律有待进行进一步的试验研究。

［1］ 罗平亚.关于大幅提高我国煤层气井单井产量的探讨［J］.天然气工业，2013，33（6）：1-6. LUO Pingya.A discussion on how to significantly improve the single well productivity of CBM gas wells in China［J］.Natural Gas Industry，2013，33（6）：1-6.

［2］ 林柏泉，李子成，翟成，等.高压脉动水力压裂卸压增透技术及应用［J］.采矿与安全学报，2011，28（3）：452-455. LIN Baiquan，LI Zicheng，ZHAI Cheng，et al.Pressure relief and permeability-increasing technology based on high pressure pulsating hydraulic fracturing and its application［J］.Journal of Mining&Safety Engineering，2011，28（3）：452-455.

［3］ 翟成，李贤忠，李全贵.煤层脉动水力压裂卸压增透技术研究与应用［J］.煤炭学报，2011，36（12）：1996-2001. ZHAI Cheng，LI Xianzhong，LI Quangui.Research and application of coal seam pulse hydraulic fracturing technology［J］.Journal of China Coal Society，2011，36（12）：1996-2001.

［4］ 李贤忠，林伯泉，翟成，等.单一低透煤层脉动水力压裂脉动波破岩机理［J］.煤炭学报，2013，38（6）：918-923. LI Xianzhong，LIN Baiquan，ZHAI Cheng，et al.The mechanism of breaking coal and rock by pulsating pressure wave in single low permeability seam［J］.Journal of China Coal Society，2013，38（6）：918-923.

［5］ 李全贵，林伯泉，翟成，等.煤层脉动水力压裂脉动参量作用特性的实验研究［J］.煤炭学报，2013，38（7）：1185-1190. LI Quangui，LIN Baiquan，ZHAI Cheng，et al.Experi-mental study on action characteristic of pulsating parameters in coal seam pulse hydraulic fracturing［J］.Journal of China Coal Society，2013，38（7）：1185-1190.

［6］ 朱红青，张民波，申健，等.低透气性煤层脉动注水增透机理研究及数值分析［J］.煤炭学报，2013，38（增2）：343-347. ZHU Hongqing，ZHANG Minbo，SHEN Jian，et al.Permeability enhancing mechanism and numerical analysis on pulsating water injection in low permeability coal seams［J］.Journal of China Coal Society，2013，38（sup2）：343-347.

［7］ 孙卫涛.弹性波动方程的有限差分数值方法［M］.北京：清华大学出版社，2009：39-46.

［8］ KELLY K R，WARD R W，TREITEl S，et al.Synthetic seismograms：a finite-difference approach［J］.Geophysics，1976，41（1）：2-27.

［9］ HUDSON J A.Wave speeds and attenuation of elastic waves in material containing cracks［J］.Geophysical Journal Royal Astronomical Society，1981，64（1）：133-150.

［10］ SCHOENBERG M.Elastic wave behavior across linear slip interfaces［J］.The Journal of the Acoustical Society of America，1980，68（5）：1516-1521.

［11］ SCHOENBERG M，DOUMA J.Elastic wave propagation in media with parallel cracks and aligned cracks［J］.Geophysical Prospecting，1988，36（6）：571-590.

［12］ COATES R T，SCHOENBERG M.Finite-difference modeling of faults and cracks［J］.Geophysics，1995，60（5）：1514-1526.

［13］ KACHANOV M.Continuum model of medium with cracks［J］.Journal of Engineering Mechanics Division of ASCE，1980，106（5）：1039-1051.

［14］ GROGENBOOM J，FALK J.Scattering by hydraulic cracks：finite-difference modeling and laboratory data［J］.Geophysics，2000，65（2）：612-622.

［15］ WU Chunling，HARRIS J M，NIHEL K T，et al.Twodimensional finite-difference seismic modeling of an open fluid-filled crack：comparison of thin-layer and linearslip models［J］.Geophysics，2005，70（4）：57-62.

［16］ 王永刚，邢文军，谢万学，等.完全匹配层吸收边界条件的研究［J］.中国石油大学学报：自然科学版，2007，31（1）：19-24. WNAG Yonggang，XING Wenjun，XIE Wanxue，et al. Study of absorbing boundary condition by perfectly matched layer［J］.Journal of China University of Petroleum（Edition of Natural Science），2007，31（1）：19-24.

［17］ 董良国.弹性波数值模拟中的吸收边界条件［J］.石油地球物理勘探，1999，34（1）：45-56. DONG Liangguo.Absorptive boundary condition in elastic-wave numerical modeling［J］.OGP，1999，34（1）：45-56.

［18］ 陆沛青，李根生，黄中伟，等.煤层脉动水力压裂动静态响应数值模型及求解［J］.岩土力学，2015，36（5）：1471-1480. LU Peiqing，LI Gensheng，HUANG Zhongwei，et al. Establishment and solution of a dynamic and static response numerical model of on pulsating hydro-fracturing in coal seams［J］.Rock and Soil Mechanics，2015，36（5）：1471-1480.

［19］ 赵振保.变频脉冲式煤层注水技术研究［J］.采矿与安全学报，2008，25（4）：486-489. ZHAO Zhenbao.Study of technology of variable frequency pulse water［J］.Journal of Mining&Safety Engineering，2008，25（4）：486-489.

［20］ 李波，张景松，姚宏章，等.高压脉动水力锤击煤层注水技术研究［J］.矿业安全与环保，2011，38（2）：14-16，19. LI Bo，ZHANG Jingsong，YAO Hongzhang，et al.Study of high pressure pulsation hydraulic hammer on coal seam affusion［J］.Mining Safety&Environmental Protection，2011，38（2）：14-16，19.

［21］ 吴百烈.煤层气井水力压裂几何参数优化设计［D］.青岛：中国石油大学石油工程学院，2011. WU Bailie.Geometry parameter designing of hydraulic fracturing［D］.Qingdao：School of Petroleum Engineering in China University of Petroleum，2011.

［22］ 蒋金宝，林英松，张宝康，等.激波作用下岩石损伤试验及评价方法［J］.中国石油大学学报：自然科学版，2008，32（3）：75-79. JIANG Jinbao，LIN Yingsong，ZHANG Baokang，et al. Rock damage experiment and evaluation method by exploding wave［J］.Journal of China University o f Petroleum（Edition of Natural Science），2008，32（3）：75-79.

［23］ 张奇.应力波在节理处的传递过程［J］.岩土工程学报，1986，8（6）：99-105. ZHANG Qi.Propagation procedure of stress waves in rock joints［J］.Yantu Gongcheng Xuebao，1986，8（6）：99-105.

［24］ LI Jianchun，MA Guowei.Analysis of blast wave interaction with a rock joint［J］.Rock Mechanics and Rock Engineering，2010，43（6）：777-787.

［25］ 柴少波，李建春，李海波.柱面波在节理岩体中的传播特性［J］.岩石力学与工程学报，2014，33（3）：523-530. CHAI Shaobo，LI Jianchun，LI Haibo.Propagation characteristics of cylindrical wave in joint rock masses［J］.Chinese Journal of Rock Mechanics and Engineering，2014，33（3）：523-530.

（编辑 李志芬）

Numerical simulation of influence of crack fillers on stress disturbance effect during pulsating hydro-fracturing

LU Peiqing，LI Gensheng，SHEN Zhonghou，HUANG Zhongwei，SHENG Mao，CHI Huanpeng
（State Key Laboratory of Petroleum Resources and Prospecting in China University of Petroleum，Beijing 102249，China）

A linear slip deformation model，a finite-difference method and staggered-grid were used to investigate the stress propagation and distribution in fractured formation during the pulsating hydro-fracturing（PHF）process，and the influence of crack fillers was analyzed at different crack intervals and source frequencies.The numerical simulation results show that the influence of mineral-filled cracks on PHF stress disturbance is weak，so that its fractured zone can be considered as homogeneous.When the crack is filled with fluid，it can cause the reflection of pressure waves，which will form a great velocity contrast between strong and weak reflection zones to generate shear stress，then causing tensile damages.However，if the crack is too close to the pulsating source，the reflected and propagated pressure waves will disturb each other and reduce the fracturing effect.The influence of gas-filled cracks is similar to that of the fluid-filled，but its reflection of pressure waves is much stronger，which means a longer crack interval can be applied to promote the stress disturbance effect.The PHF technique can be used in coal seams with fracture anisotropy to increase their permeability.When the interval between initial artificial fractures and natural fractures is 2-3 times larger than the length of initial artificial fractures，a better PHF stress disturbance effect can be acquired.

pulsating hydro-fracturing；linear slip deformation model；crack fillers；stress disturbance effect；optimal interval

TE 357.11

A

1673-5005（2015）04-0077-08

10.3969/j.issn.1673-5005.2015.04.010

2014-08-30

国家自然科学基金项目（51221003）；国家科技重大专项（2011ZX05037001）

陆沛青（1988-），男，博士研究生，研究方向为煤层气增产机制与技术。E-mail：lupeiqingsydx@163.com。

引用格式：陆沛青，李根生，沈忠厚，等.裂缝充填物对脉动水力压裂应力扰动效果的数值模拟［J］.中国石油大学学报：自然科学版，2015，39（4）：77-84.

LU Peiqing，LI Gensheng，SHEN Zhonghou，et al.Numerical simulation of influence of crack fillers on stress disturbance effect during pulsating hydro-fracturing［J］.Journal of China University of Petroleum（Edition of Natural Science），2015，39（4）：77-84.