基于核线影像的点特征提取与图像匹配方法比较研究

欧阳君

摘要：对遥感航空影像进行计算机自动化处理是目前遥感发展的主要方向，而特征提取与影像匹配是一切影像处理的前提。特征提取算子有很多，该文比较和评价了几种著名的特征提取算子：Moravec算子、Harris算子和Forstner算子。基于相关系数以及最小二乘方法，利用提取出的特征点将两幅核线影像进行匹配与校正，比较和评价了两种匹配方法，并对最小二乘匹配方法作出了一些改进。

关键词：影像匹配最小二乘法特征提取核线影像

中图分类号：P203 文献标识码：A 文章编号：1672-3791（2015）07（b）-0000-00

随着图像信息处理技术的不断发展，图像特征和影像匹配的研究已成为该领域两个重要的研究方向。许多摄影测量和计算机视觉工作将特征提取作为最初的处理步骤以便后续的处理和分析。图像特征提取是影像分析和影像匹配的基础，影像匹配是图像融合、目标识别、目标变化检测、计算机视觉等问题中的一个重要前期步骤。

图像的特征可分为点、线、面三种[1]。点特征可以应用于诸如图像的匹配，目标描述与识别，光束计算，运动目标跟踪、识别和立体像对3D建模等众多领域。使用点特征进行处理，可以减少参与计算的数据量，同时又不损害图像的重要灰度信息，在匹配运算中能够较大的提高匹配速度。在视觉方面的应用中，面特征也被用于目标探测、目标识别、目标分类和自动地宽基线图像定位[2]。

影像匹配可以用于重建景物的三维影像、机器人视觉、地理信息系统、生物医学成像、DEM 自动生成甚至虚拟现实等领域都有着广泛的用途[3]。

1 数据源及操作平台

该文以两幅raw格式卫星核线影像作为数据源进行特征提取以及影像匹配，两幅影像间存在几何畸变和辐射畸变。

2 点特征提取

特征提取是影像处理过程中的第一步，它减少了需要处理的数据量并从影像中提取出了

最突出的特征。点特征提取是最常采用的一种图像特征提取，主要指明显点，如角点、圆点等。提取特征点的算子称为兴趣算子或有利算子，即运用某种算法从影像中提取我们所感兴趣的即有利于某种目的的点。该文比较了三种著名的特征提取算子，分别是：Moravec算子、Harris算子和Forstner算子。

Moravec 算子是 Moravec 于1977年提出利用灰度方差提取点特征的算子，是第一个提出兴趣点概念的算子。Harris算子是传统 Moravec 算子的改进，它在自相关函数的帮助下解决了离散变化和方向的问题，并且提高了定位精度[4]。Forstner 算子是摄影测量中著名的定位算子，其特点是速度快，定位精度较高。通过计算各像素的Roberts梯度和像素的协方差矩阵，在影像中寻找具有尽可能小的接近圆的误差椭圆的点作为特征点。

a Moravec 算子 bHarris 算子 cForstner 算子

图1三种特征提取算子对同一幅卫星影像提取的细节图

Moravec算子（图1a）几乎可以检测到所有的角点。Moravec角点提取算子是一个相对简单的算子，它最显著的优点是实现简单快速。它对强边缘比较敏感，这是由于响应值是自相关的最小值而不是差值。它不是旋转不变性的。Moravec算子对噪声敏感，它容易把沿着边缘的点和孤立的点作为角点，常常会提取出错误角点。

Harris算子（图1b）可基本检测到所有的角点，但是对某些特征点的定位不准确，也有一些错误角点，但是仍然比Moravec算子的效率高。通过增设阈值可以减少错误角点，提高效率。Harris算子具有计算简单、提取的点特征均匀而合理、可定量提取特征点以及算子较为稳定等优点[5]。且Harris算子的复杂程度介于Moravec算子和Forstner算子之间，在实际处理过程中是很受欢迎的算子之一。

Forstner算子（图1c）的计算速度较快，相比于Harris算子计算精度较高，但是对于Forstner算子来说，需要设置两个阈值，且不同图像需要设置不同的阈值，这两个阈值的确定提取出特征点的数量以及配准精度有很大影响。对于对比度小的影像，若阈值设置过大，则提取出的特征点数量较少，不利于后续的匹配工作；对于对比度大的影像，若阈值设置过小，则提取出的特征点数量较多，对匹配工作产生严重的运算负担；若阈值设置的较合适，则可提取出较好的特征点。

3 影像匹配

图像匹配，也称为图像配准，是图像处理的基本任务之一，可广泛用于目标识别与跟踪、立体视觉、变化检测、测绘等领域。在图像匹配的过程中，需要注意的地方有很多，主要可以归结为以下几个方面[6]。

（1）特征空间的选择。根据上文特征提取的结果，采用Harris算子提取出的特征点作为影像匹配的特征空间，原因如下：Harris算子计算简单，提取的点特征均匀而合理，可定量提取特征点，且算子较为稳定。相较于Moravec算子，Harris算子提取特征点的效率和精度较高，错误点较少，提取出的特征点总数较少，角点基本上都可以提取。相较于Forstner算子，Harris算子不需设定阈值，可做到自动提取特征点，复杂程度较低。

（2）相似性测度的选择。采用两种相似性测度，分别为相关系数和最小二乘，并将两种测度所得结果进行比较。

（3）搜索空间与策略的选择。采取的数据源为核线影像，沿核线的一维相关可用一维目标区， 但为了提高相关的质尼，采用二维目标区进行沿核线的一维搜索。这样既可比二维相关成平方地减少工作量，又可获得高的相关质量[7]。

3.1相关系数

相关系数法影像匹配就是以相关系数作为匹配测度进行两张影像的影像匹配，在左影像内取一适当大小窗口作为目标区影像，右影像取一大于目标区的窗口作为搜索区影像，在搜索区内取与目标区影像同样大小的窗口，计算两窗口的相关系数，不断移动搜索区内窗口，找到搜索区内与目标区影像相关系数最大的位置，得到右影像关于左影像的偏移量。相关系数是标准化后的协方差函数，以协方差函数除以两信号的方差即得相关系数。

由于该文采取核线影像作为数据源，可只计算右影像相对于左影像在水平方向上的偏移。在具体搜索时，有两种方法可以选择：（1）以左影像提取出的特征点作为目标区影像窗口的中心点，与右影像同名核线上的所有点进行匹配计算相关系数；（2）以左影像提取出的特征点作为目标区影像窗口的中心点，与右影像同名核线上的特征点进行匹配计算相关系数。第一种方法提取的同名点对数较多，但运算速度较慢。而第二种方法提取的同名点对数较少，运算速度却可以大大提升。该文采用第二种方法。当两窗口间的相关系数大于0.95时定义为同名点。

3.2最小二乘匹配

最小二乘影像匹配的方法由德国Ackermann教授提出，该方法充分利用了影像窗口内的信息进行平差计算，使影像匹配可以达到1/10甚至1/100像素的高精度，即可达到子像素等级，因此被称为“高精度影像相关”。最小二乘影像匹配方法具有灵活、可靠和高精度的特点，受到了广泛关注，得到了很快的发展。

但是，最小二乘影像匹配方法存在某些缺点，即当初始值不太准确时，系统的收敛性不好。为了解决这个问题，该文采用相关系数计算出的两个同名点之间的偏移量作为初始值，带入到最小二乘的几何校正参数模型中，结果证明此方法可以大大提高最小二乘匹配方法的收敛性。

该文的另外一个创新点为，在进行最小二乘迭代前，将相关系数大于0.8的特征点全部输入，进行最小二乘迭代计算后，将相关系数大于0.95的特征点定义为同名点，这样可以提出由于辐射和几何畸变等原因造成的相关系数较小或未到达0.95的同名点，增加提取出的同名点对数。

3.3匹配方法比较

a 左影像 b右影像

图2相关系数匹配细节图

a左影像 b右影像

图3最小二乘匹配细节图

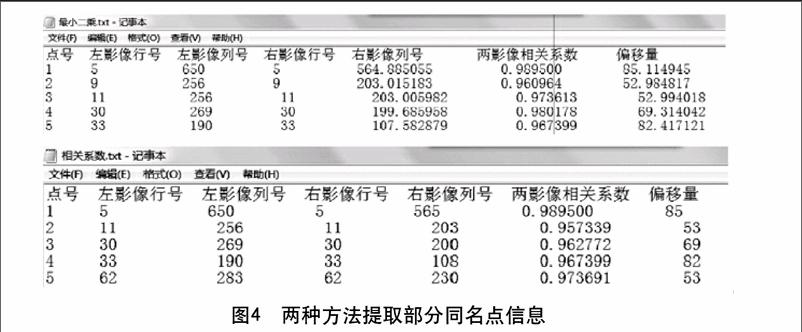
图4两种方法提取部分同名点信息

由于图像显示原因，对于提取出的特征点只能显示整像素，但在输出的txt文件中可以看到定位的精度已到达子像素。另外，可以从细节图中看到，应用该文设计算法时的思路，最小二乘在细节图的左下角比相关系数多提取出一对同名角点，且精度很高，txt文件中也可以看到最小二乘方法比相关系数方法存在多提出的同名点，如第9行的同名点。在整幅图像中，相关系数共提取出36对同名点，而最小二乘则提取出了49对同名点，通过目视判读，均为正确的同名点，证明了该文思路的可行性。

相关系数和最小二乘匹配方法各有优缺点，相关系数法比较简单，计算速度快，相关系数测度是标准化的协方差函数，由于它是灰度线性变换的不变量，当目标影像的灰度与

搜索影像的灰度之间存在线性畸变时，仍能较好地评价它们之间的相似程度，虽不能改正目标影像与搜素影像之间的几何畸变，相关系数匹配方法平时仍然较为常用。

最小二乘方法可以改正目标影像与搜索影像之间的辐射畸变和几何畸变，且可将匹配的精度达到子像素级。最小二乘方法较相关系数法复杂一些，且存在难以收敛等缺点，但是经过该文对于初始值设定的改进，已很好地提升了最小二乘方法的收敛性。

4 结语

该文以两幅卫星核线影像数据为例，经过特征提取、影像匹配得到两幅影像之间的偏移量，并对特征提取方法以及匹配方法进行了比较与评价，并提出以下两个创新点。

（1）针对最小二乘匹配方法变形参数初始值的设定问题，提出了较为简单的解决方法，实验结果证明，该方法可有效地提升最小二乘的收敛性，且保证了匹配的精度。

（2）在进行最小二乘迭代前，先定义一个小的相关系数阈值，将大于这个阈值的同名点进行最小二乘迭代，最终使用与相关系数阈值相同的阈值定义同名点，通过实验证明，相对于相关系数匹配方法增加了提取出的同名点对数，且精度较高。

参考文献

[1] 张剑清，潘励，王树根.摄影测量学[M].武汉：武汉大学出版社，2013：121.

[2] 谢东海，詹总谦，江万寿.改进Harris算子用于点特征的精确定位[J].测绘信息与工程，2003（2）：22-23.

[3] 陈淑荞.数字图像特征点提取及匹配的研究[D].西安：西安科技大学，2009.

[4] 张剑清.基于特征的最小二乘匹配理论精度[J].武汉测绘科技大学学报，1988（4）：82-90.