低温超导微波频率源的实验研究

王暖让，李陟，杨永军，年丰，高连山

（1.北京无线电计量测试研究所 计量与校准技术重点实验室，北京 100854；2.中国航天科工集团 第二研究院研究生院，北京 100854；3.北京长城计量测试研究所，北京 100095）

低温超导微波频率源的实验研究

王暖让1，2，李陟2，杨永军3，年丰1，高连山1

（1.北京无线电计量测试研究所 计量与校准技术重点实验室，北京 100854；2.中国航天科工集团 第二研究院研究生院，北京 100854；3.北京长城计量测试研究所，北京 100095）

针对低温超导微波频率源的研制，通过理论分析和仿真设计，得到了其优化设计方案，主要涉及高Q值超导腔、高稳定低温环境及锁相稳频环路等组件/技术的研究，并完成了系统闭环实验测试。实验表明，超导腔的Q值最高达到1.9×109，低温环境温度达到1.6 K，温度稳定度优于0.000 4 K，微波源的频率稳定度最高可达到4.6×10-15/1s。

频率标准；超导稳频振荡器；微波腔；品质因数

0 引言

频率源是现代电子设备的心脏，随着电子技术的飞速发展，对频率源的时间和频率性能要求也越来越高。高频率、高稳定、低相噪的频率源已经成为现代军事电子系统、测绘、导航、通信、电子战争和导弹制导等系统中的重要设备。同时，空间技术高速发展的今天，近地空间及远地空间飞行器的测控、制导、通信、数据传输和地面目标的定位，都需要高稳定的频率源。

超导稳频振荡器（SCSO）是目前应用最广及最有潜力的低温超导微波频率源，其关键物理部分——超导腔具有极高的Q值（107～109）及非常小的温度系数[1-3]，因而其短期频率稳定度远远超过了传统原子钟（氢钟、铷钟、铯钟等），最高可以达到10-14～10-15量级（1 s<τ<1 ks）[4-6]，是当前性能优良的中短稳（1 s<τ<100 s）标准。有关用于低温超导微波频率源设计的文献较少，一般集中在美国斯坦福大学、日本无线电研究所和美国加州理工大学。这些研究所从19世纪60年代就开始了对超导腔的研究，并取得了很大的进展。美国斯坦福大学Buchman等人利用频率8.6 G的铌腔，电子束焊接而成，并经高温高真空退火、化学处理，工作模式为TM010，工作温度为1.2 K的环境下进行测试，得到的短期频率稳定度最高可达10-15量级（30 s<τ<1 ks）[7]。另外法国和ULISS西澳大利亚大学等研究机构开展了低温蓝宝石频率源的研究，蓝宝石微波腔的Q值在108～109之间，频率源的短稳可达到10-15～10-16量级[8-9]。

国内也曾开展过SCSO的研究工作，但是没有得到满意的结果，其主要原因是超导腔的Q值不高，一般低于108，109很难达到。西南交通大学超导研究中心曾在低温铌超导微波谐振腔系统和低温铌超导微波表面电阻方面开展过研究工作，并取得一定研究成果，后因故放弃此方面的研究；北京无线电计量测试研究所多年前开展SCSO的研究，已取得较大进展[10-11]；此外，国内很多机构例如中国科学院高能所及北京大学等单位，利用超导腔进行粒子加速器的研究，此类超导腔频率一般较低，大多在1 GHz以下[12-14]。本文根据电磁场微波理论建立了SCSO稳频环路解析方程、微波腔输入输出端耦合系数表达式；通过理论计算得到微波腔的最佳工作点，并通过有限元及时域有限差分电磁仿真软件对理论计算得到的尺寸进行仿真设计，设计出高Q超导腔。实验表明，微波腔的Q值可达到1.9×109，达到国际同等水平，SCSO的秒稳达到4.6×10-15，这是在已有SCSO文献中最高的。

1 理论部分

图1是高稳定超导微波频率源的原理框图。如图1所示，工作在真空杜瓦中的超导微波腔是SCSO的核心，它具有很高的Q值，作为一个“基准”对外部馈入的微波信号进行鉴频。外部微波信号由介质振荡器（DRO）产生，调制振荡器进行相位调制得到的。调制微波信号经过超导微波腔的鉴频，再通过外部检波和放大电路，得到外部微波信号与超导微波腔谐振中心频率之差的误差信号，利用此误差信号转换成电压信号去调整介质振荡器的频率，从而实现超导稳频。

图1　高稳定超导微波频率源原理框图

1.1 系统理论模型

超导腔在稳频环路中起鉴频的作用。工作流程如下：介质振荡器（DRO）输出信号经功分器后，一路作为输出信号，另外一路经相位调制，调制频率为fm，调制频率远远大于超导腔有载Q值的3 dB带宽。信号经超导腔后进入检波器，检测到的信号经放大后与调制源经移相后进行混频/检波，得到输出信号Vx如下式所示[15]：

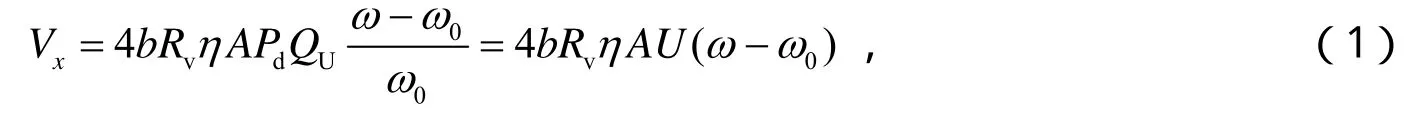
式（1）中，b为电流灵敏度，Rv为平方律检波器的阻抗，η为第一边带与载波幅度的比值，A为放大器和混频/检波器的增益之和，Pd为超导腔损耗的能量，ω0=2πf0为超导腔的谐振频率，U=PdQU/ω0为超导腔的储能，QL和QU分别为超导腔的有载Q值和无载Q值。

通过拉布拉斯变换，SCSO的频率波动Δω（s）可表示为

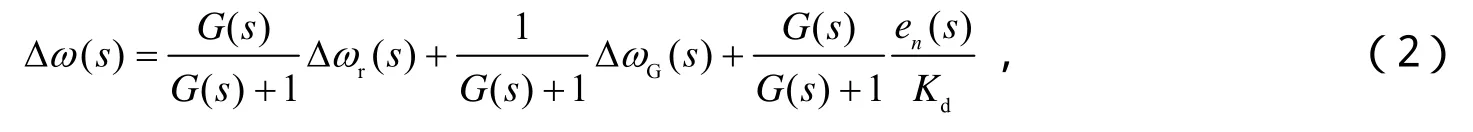
式（2）中，Δωr（s）为超导腔频率的波动，ΔωG（s）为DRO自由工作时的频率波动，en（s）为鉴频器的输出噪声电压，Kd=4bRvη AU为鉴频器的灵敏度，G（s）为开路环路增益，式（2）等号右边第3部分表示鉴频器信噪比S N引起的频率波动，并且当ΔωG（s）足够小时，SCSO的短期频率稳定度主要由S N限制。

在鉴频环路中，检波器能够引起频率牵引。

信号经超导腔后输出的信号如下式所示：

1.2 微波腔的设计及仿真

超导腔设计需要考虑的因素主要包括：频率、Q值、工作模式、工作温度。其中Q值尤为重要，其直接影响超导腔稳频器的短期稳定度。TM010模式为低次模，并且其工作区域较大，所以选择此模式为工作模式，下面对此模式进行分析。

TMnip模式的公式为[16]

根据文献[16]，我们可以得到圆柱形谐振腔TM010模式的Q值计算公式为

由式（16）可见，要得到Q值，必须首先得到表面电阻Rs的值。而液氦温度下，超导体的表面电阻并不为0，它由两部分组成，如下式所示：

式（18）中，RBCS为BCS电阻，R0为剩余电阻，通常与环境剩磁大小、材料本身的杂质、材料的表面处理或在表面的凝结有关，与温度无关。BCS电阻[17]的计算公式为

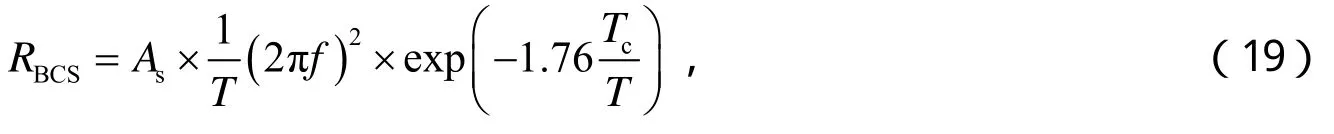
式（19）中，Tc为材料达到超导的临界温度，超导状态下表面剩余电阻R理论值为100 nΩ。

下面对Q值进行编程计算，得到Q值在1～4.2 K温度范围内随温度的变化。将已知频率带代入式（19），可以得到BCS电阻为：当T=4.2 K 时，当T=2 K时，将以上有关数据代入式（15），可以解得微波腔的Q为：当T=4.2 K 时，Q=9.3× 106；当T=2 K时，Q=3.76× 109。

通过Matlab编程计算得到如图2所示曲线。由图2中可以看出在，当温度在3K到2 K之间时，Q 值随温度的变化非常剧烈，而当温度小于2 K时，Q值的变化就比较平坦，所以我们要达到所要求的指标，必须使温度保持在2 K以下。

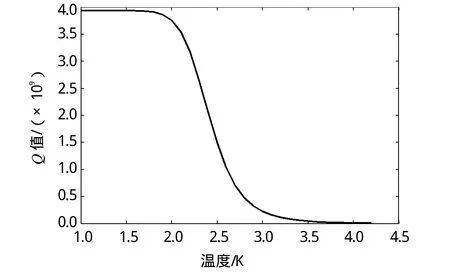
图2　微波腔Q值随温度的变化曲线

图3是腔示意图，经理论计算及仿真设计得到圆柱腔的尺寸：直径D=50 mm ，高度l=26.5 mm ，频率f=4.7 GHz 。通过计算及仿真可得到束管的尺寸l1=l2=50 mm ，r1=r2=10 mm ；输入端天线（Pin）插入深度为24.5 mm，输出端天线（Pout）插入深度为19.5 mm。该部分的仿真详见文献[9]。

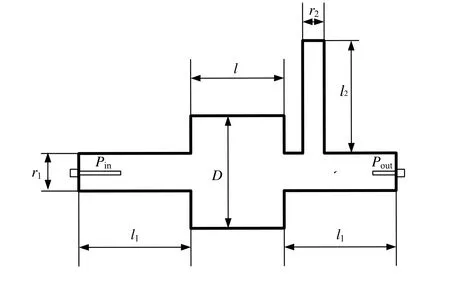
图3　腔示意图

2 实验研究

整个系统实验超导腔组装完毕后抽真空，同时进行低温烘烤，当真空度达到10-6Pa量级时，抽真空结束后即可进行实验系统的组装并进行液氦的灌注，根据液面显示仪的读数进行灌注，灌满所用时间为4 h。此时杜瓦内温度为4.2 K，利用矢量网络分析仪进行测试，得到的参数为：f=4.4 GHz ，Q=3.2× 107。测试完毕即进行减压降温，首先开一个干泵，利用针阀调节抽气速度，根据压力表的读数，使杜瓦内压力平稳下降。随着压力的下降，温度逐渐下降，但是速度越来越慢，打开另外一个干泵使两个干泵并联抽气，控制针阀及真空阀，使杜瓦内最后温度平稳在1.6 K，然后进行测试，得到的参数如下：f=4.4 GHz ，Q=1.92× 109，如图4所示。

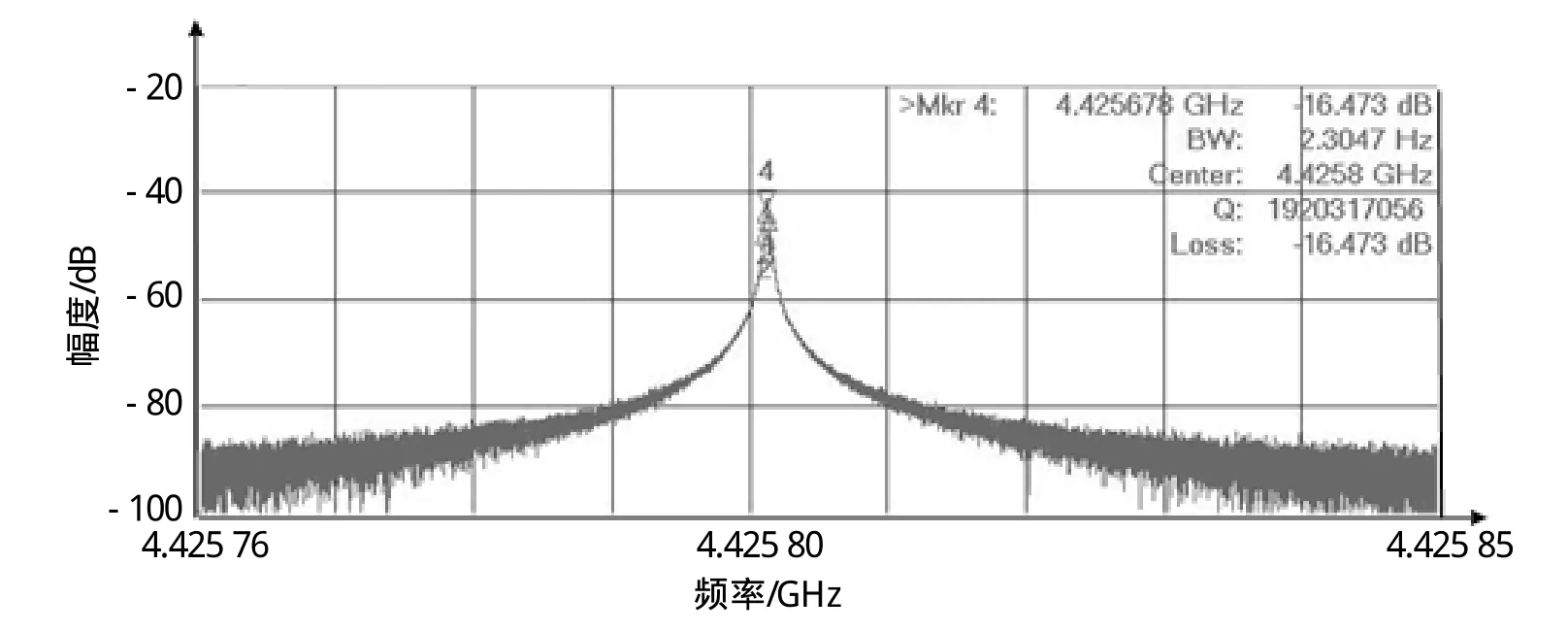
图4　超导腔参数测试图

图5是系统连接示意图。其中铌材谐振腔上装有信号输入输出耦合装置，根据使用的模式电磁场分布特点，输入输出耦合装置为探针耦合器，探针长度经过严格的电磁场仿真计算得到；电路主要完成出入腔信号的频差检测，并使用经超导腔检测出的误差信号来控制晶振，形成反馈控制环路，部分微波器件需要放置在液氦中，其部分设计参考了文献[18]；液氦低温杜瓦是为了满足在测量过程中需要的低温环境，同时为了保证测量中有足够的液氦，低温杜瓦的静态漏热应小于2 W；磁屏蔽的作用是屏蔽空间磁场，减小由空间外磁场带来的表面剩余电阻；减压降温系统的作用是，通过降低低温杜瓦内部的压力使液氦的沸点从4.2 K降到1.6 K，温度的降低将会减小超导腔表面BCS电阻。环路锁定后采用差拍法[19-20]进行测试，两套SCSO混频得到的约19.5 MHz信号与参考的10 MHz信号同时输入到频率稳定度测试仪，得出测试结果，1 s频率稳定度测试结果可达1.5×10-12，因此经过计算可得到超导稳频振荡器的频率稳定度:

图5　高稳微波频率源装置及测试框图

式（20）中，0σ为SCSO的频率稳定度，xf为SCSO的频率，0f为两套SCSO的拍频，xσ为拍频0f的频率稳定度。进行换算可得到SCSO的频率稳定度如图6所示，其中秒稳达到4.6×10-15，这是目前相关SCSO文献报道中最高的。

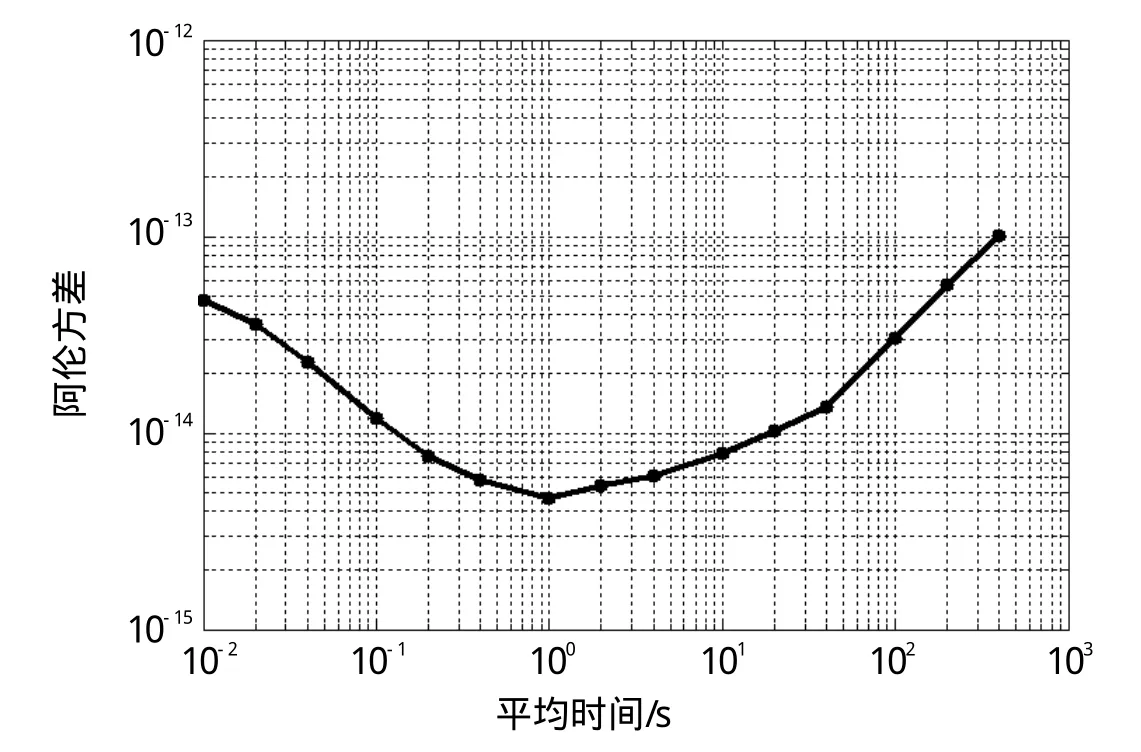
图6　测试结果曲线

3 结论

利用电磁场微波理论建立了SCSO稳频环路解析方程、微波腔输入输出端耦合系数表达式；通过理论计算得到微波腔的最佳工作点，并通过有限元以及时域有限差分电磁仿真软件对理论计算得到的尺寸进行仿真设计，设计出高Q超导腔。实验表明，微波腔的Q值可达到1.9×109，位于国际同等水平，SCSO的秒稳达到4.6×10-15，这是在已有SCSO文献中最高的。目前正在进行SCSO系统的优化及着手建立国家最高短稳标准等相关工作。

[1]AZARYAN N S, BATURITSKY M A, BUDAGOV Y A, et al.Measuring of ultrahigh unloaded Q factor using excitation of a superconducting cavity by the electron beam[J].Physics of Particles and Nuclei Letters, 2013, 10(7): 788-794.

[2]AZARYAN N S, BATURITSKY M A, BUDAGOV Y A, et al.Computation of single cell superconducting niobium cavity for accelerator of electrons and positrons[J].Phys.Part.Nucl.Lett., 2012, 9(2): 150-153.

[3]WATANABE K N, NOGUCHI S, KAKO E, et al.Development of the superconducting rf 2-cell cavity for cERL injector at KEK[J].Nuclear Instruments and Methods in Physics Research A, 2013, 714: 67-82.

[4]YEH N C, STRAYER D M, ANDERSON V L, et al.Superconducting-cavity-stabilized oscillators(CSMO) for precise frequency measurements[J].Physica B, 2000, 280: 557-558.

[5]BLOMFIELD D L H, POINTON A J.Short-term frequency stability of an L band oscillator with a superconducting cavity[J].Electronics Letters, 1973, 9(19): 461-462.

[6]CIOVATI G, KNEISEL P.Preliminary results on the simultaneous excitation of the TM010and TE011modes in a single cell Niobium cavity[C]// IEEE Proceedings of 2005 Particle Accelerator Conference, Knoxville: IEEE, 2005: 3844-3846.

[7]BUCHMAN S, TURNEAURE J P, LIPA J A, et al.A superconducting microwave oscillator clock for use on the Space Station[C]// IEEE Proceedings of 1998 International Frequency Control Symposium, Pasadena, California: IEEE, 1998: 534-539.

[8]GIORDANO V, GROP S, DUBOIS B, et al.New-generation of cryogenic sapphire microwave oscillators for space, metrology, and scientific applications[J].Review Of Scientific Instruments, 2012, 83: 085113.

[9]NAND N R, PARKER S R, IVANOV E N, et al.Resonator power to frequency conversion in a cryogenic sapphire oscillator[J].Applied Physics Letters, 2013, 103(4): 043502.

[10]WANG Nuan-rang, WU Qiong, NIAN Feng, et al.Recent progress on a superconducting microwave cavity for frequency standard[C]// 10th International Conference on Electronic Measurement & Instruments, Chengdu, China: IEEE, 2011: 238-241.

[11]王暖让, 年丰, 高连山.超导稳频振荡器微波腔的优化设计[J].时间频率学报, 2013, 36(1): 9-15.

[12]郝建奎, 焦飞, 黄森林, 等.提高射频超导加速腔性能的表面干式处理研究[J].物理学报, 2005, 54(7): 3375-3379.

[13]葛明骐, 赵生初, 孙虹, 等.1.3 GHz单cell高梯度低损耗超导腔设计研究[J].高能物理与核物理, 2006, 30(4): 354-358.

[14]温华明, 严陆光, 林良真.超导在加速器中的应用概况[J].低温与超导, 2005, 33(1): 46-49.

[15]KOMIYAMA B.A 9.2 GHz superconducting cavity stabilized oscillator[C]// Proceedings of 39th Annual Symposium On Frequency Control, Philadelphia, Pennsylvania, USA: IEEE, 1985: 159-165.

[16]POZAR D M.Microwave Engineering[M].3rd ed.New York: John Wiley & Sons, 2005: 245.

[17]XIAO B P, REECE C E, KELLEY M J.Superconducting surface impedance under radiofrequency field[J].Physica C, 2013, 490: 26-31.

[18]DEVORET M H, SCHOELKOPF R J.Superconducting circuits for quantum information: and outlook[J].Science, 2013, 339(6124): 1169.

[19]BIZS E, LAURENT P, ABGRALL M, et al.Cold atom clocks and applications[J].J.Phys.B: at.Mol.Opt.Phys.2005, 38: S449-S468.

[20]LING Hao, KLEIN N, GALLOP J C, et al.Temperature compensated cryogenic whispering gallery mode resonator for microwave frequency standard applications[J].IEEE Transaction on Instrumentation and Measurement, 1999, 48(2): 524-527.

A study of cryogenic superconducting microwave frequency source

WANG Nuan-rang1，2，LI Zhi2，YANG Yong-jun3，NIAN Feng1，GAO Lian-shan1
（1.Science and Technology on Metrology and Calibration Laboratory，Beijing Institute of Radio Metrology & Measurement，Beijing 100854，China；2.Graduate Schools，Second Academy of China Aerospace，Beijing 100854，China；3.Changcheng Institute of Metrology & Measurement，Beijing 100095，China）

A optimized design of cryogenic superconducting microwave frequency source is achieved based on theory analysis and computer simulation.The design involves superconducting cavity with high quality factor，highly stable and cryogenic environment，phase-looked loop and so on.The closed-loop tests were completed and the experiments show that the quality factor of cavity reaches 1.9×109，the environment temperature is 1.6 K，the temperature stability is better than 0.000 4 K and the frequency stability for 1 s reaches 4.6×10-15.

frequency standard； superconducting cavity stabilized oscillator； microwave cavity； quality factor

TH714.+4

A

1674-0637（2015）02-0065-08

10.13875/j.issn.1674-0637.2015-02-0065-08

2014-12-08

国防技术基础科研资助项目（J042011C001）

王暖让，男，博士，主要从事原子频标技术研究。