基于小生境遗传算法的两栖车辆车轮收放装置的优化

包振明，王琪，徐一新，唐苏

（1.江苏科技大学能动学院，江苏 镇江 212003；2.江苏科技大学机械学院，江苏 镇江 212003）

基于小生境遗传算法的两栖车辆车轮收放装置的优化

包振明1，王琪2，徐一新2，唐苏2

（1.江苏科技大学能动学院，江苏 镇江 212003；2.江苏科技大学机械学院，江苏 镇江 212003）

文章根据水陆两栖车辆的车轮收放装置的特点, 建立改进型双横臂独立悬架的静力学和运动学模型，运用小生境遗传算法，在MATLAB中开发了多目标的优化程序，通过高次迭代排除干涉项，求取到了全局最优解。并进一步在 ADAMS中建立悬架的运动学模型，验证其优化设计的可行性，仿真分析表明，优化后的结果达到悬架设计的性能指标，是一种水陆两栖车辆车轮收放装置中悬架系统的有效设计新方法。

两栖车辆；双横臂独立悬架；车轮收放装置；小生境遗传算法

10.16638/j.cnki.1671-7988.2015.09.015

CLC NO.: U463 Document Code: A Article ID: 1671-7988(2015)09-41-05

引言

两栖车辆的发展中，水阻力一直是影响车辆水中行驶速度的主要因素之一。而车轮在水中形成的附着阻力占总的水阻力比率相对较大。因此，如何在水中将车轮收起以实现减阻增速是两栖车辆研究的关键之一[1-2]。现有的车轮收放装置有两种，一种为垂直升降车轮，另一种是翻转式收放车轮[3-4]。这两种都是通过对悬架导向机构进行改进，从而达到收放车轮的目的。其中翻转式车轮收放装置结构操作较为稳定，且对垂直方向的空间要求相对较低，更能符合悬架的空间布置。

两栖车辆中车轮收放对悬架的结构产生了影响，而悬架的运动特性直接与车辆在陆地行驶过程中的操纵稳定性、行驶平顺性和轮胎使用寿命等因素相关。故建立、求解悬架的运动学模型，确定悬架的空间几何参数、变化规律对整车性能有重要意义。由于双横臂独立悬架具有轮距变化小、车轮相对车身跳动时车轮定位参数变化小、结构紧凑等优点，在轮式车辆上得到广泛应用，同时也适应于两栖车辆。因此，针对双横臂独立悬架一些学者运用多体动力学、矢量法等不同的数学方法求解运动特性，并进行优化设计[5-9]。还有学者结合采用权重值系数变换法将多目标转化为单目标的遗传算法，求解不同侧重问题的最优解，以改善悬架某方面的运动特性[10-12]。还有一些学者基于 ADAMS，通过建立虚拟样机模型，通过随机的改变模型参数，以提高导向机构的运动特性[13-15]。

本文针对改进的两栖车双横臂独立悬架，结合有限转动张量，建立了悬架的数学模型，通过小生境遗传算法（NGA），设立多目标的优化算法，以求得高次迭代后的最优解。并于ADAMS中建立车辆模型，用以验证所求解收放装置的合理性。

1、数学模型的建立

1.1简化车轮收放装置的空间几何模型

双横臂独立悬架的结构示意如图1所示。为了实现车轮的主动收放，设计一种主动控制的油气弹簧悬架，并对双横臂独立悬架进行改进，将传统A字横臂拆开，得到收放装置的机构模型，如图2所示。图2中和A′′ H为下摆臂，绕轴线GH转动，取GH中点为D；EB′和B′′ F为上摆臂，绕轴线EF转动，取EF中点为C。A、B点分别为上下球节点，即AB表示主销轴线；W点为车轮中心，车轮轴线WN交AB于N点；K点为轮胎接地点，且WN⊥WK；M、P点分别为横拉杆内外球节点，转向节臂MJ交AB于J点，且MN⊥AB。为了分析导向机构的运动，动坐标系的原点O选在车轮中心和车辆中心平面的交点上，过O点的平行于车辆前进方向（平行于汽车的纵向轴线）为X轴的正向，Z轴为垂直向上。Y轴通过O点并与X轴与Z轴正交，指向车轮。

1.2收放装置的静力学模型

由于 B′ B′和A′ A′相对整体导向机构的长度较小，所以在设计计算中可以忽略。故收放装置在横向和纵向平面投影，如图3和4所示。并由悬架的空间布置，知K点坐标（0,T/2,-r）和车轮外倾角α，得W点坐标：

B点坐标为

C点坐标为：

同理可求得D点坐标。

机构于水平面的投影，如图5。根据已求得的C、D的坐标，EF在纵向平面上的投影与X轴的夹角，EF在纵向平面上的投影与X轴的夹角 θ3，可以求得E、F点的坐标。E点的坐标为：

同理可得，F、G、H点的坐标。则可知机构的瞬时中心IC的坐标，IC的坐标为：

侧倾中心高度可得：

及车轮侧偏量

1.3收放装置的运动学模型

设车轮激振过程中，下横臂和上横臂分别绕各自的方向矢量转动σ和ω角，则根据系统动力学中的有限转动张量原理，求取转角σ和ω之间的关系为：

A′为A点绕方向轴线 EF旋转某一角度σ后得到的。根据空间运动学的空间坐标变换原理，A′的坐标为：

而

由于E、F、G、H、P点的坐标没有变化，根据空间几何解析，有M点到A、B、P的距离不变，则

瞬时主销内倾角

瞬时主销后倾角

车轮前束量

2、小生境遗传算法（NGA）

2.1小生境遗传算法原理

小生境思想源于一种奇特的生物现象：在一定的生存空间下，相似的生物必须通过相互竞争以取得各自有限的生存资源，而相异的个体由于生活习性的较大差异很少竞争；从而物种生活在各自的特定的环境下。此种生存环境，被称为小生境（Niche）［16］。

小生境的基本思想是：在多元多峰值函数的优化过程中，首先将解空间划分为多个小生境域，再让相似个体在特定的小生境域中不断进化，以达到该生境域内的峰值，最后在全生境的峰值间寻求最优解。小生境遗传算法可以有效提高传统遗传算法的优化效率；并避免陷入局部最优解。

2.2设计变量

根据上述表达式及悬架导向机构的空间情况，确定设计变量为：

1）下摆臂球销转动中心点A（xa,ya,za）；

2）下摆臂长度 lAD；

3）上下摆臂长的比值 c1；

4）主销与下摆臂的比值 c2；

5）静平衡状态时，上下摆臂于横向平面中的倾角θ1、θ2；

6）上下摆臂转轴的斜置角θ3、θ4；

7）上下摆臂与X轴的夹角θ5、θ6；

8）转向节臂球外铰点M（xm,ym,zm）；

10）主销内倾角β、主销后倾角δ、车轮外倾角α。

因此设计变量为21个，即：

2.3 目标函数

根据悬架的设计要求，可确定车轮收放装置在优化设计中的目标函数如下。

1）前轮各定位参数特性。表达式为：

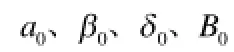
2）为减小轮胎的磨损，尽量减小轮胎侧滑量的表达式为：

3）为减小汽车在制动和加速行驶时因惯性力产生的载荷转移而导致的制动时的“点头”和驱动加速时的“抬头”现象，悬架系统应具有足够的抗点头效果。抗点头率的表达式为：

其中h为汽车质心高度；L为轴距；r为制动力分配系数；e为点IC′的高点；d为点IC′在X轴上的绝对值。当车辆整体参数确定时，h、L、r都为固定值，则抗点头率的表达式为：

根据设计要求，此悬架具有收放功能，故导向机构运动空间所占体积应该尽量最小，以减少运动干涉及轮舱体积，则体积的表达式为：

2.4约束条件

本文根据车轮收放导向机构的设计要求，确定如下约束条件：

2）下摆臂长度0≤lAD≤maxlAD；

3）上下摆臂长的比值0.6≤c1≤1；

4）主销与下摆臂长的比值0.6≤c2≤1；

2.5算法的实施

本文采用并列选择法来求解多目标优化问题的最优解，即先将群体中的全部个体按子目标函数的数目均等地划分四份，对每个子群体分配一个子目标函数，各子目标函数在各自的群体中进行运算，从而选择出一些适应度高的个体，并将这些个体组成一个新的子群体，然后再将所有新群体组成一个完整的群体，在新的群体中进行交叉和变异运算，如此不断地“分割—并列选择—合并”，以求得最优解。

3、车轮收放装置的仿真模型

根据所得解和车体结构， 利用ADAMS软件， 建立如图6所示的收放装置的运动学仿真模型， 并确定各点参数如表 1所示。

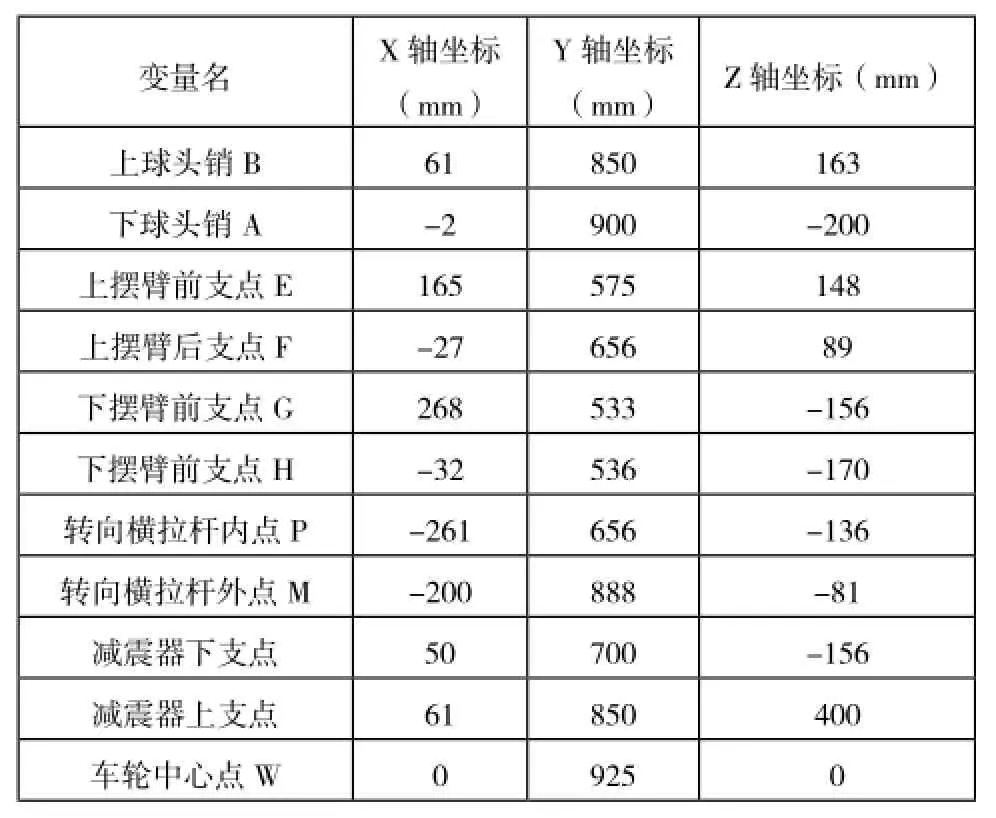
表1 前悬架各定位点的坐标

由于ADMAS模型中没有油气弹簧模型，故使用螺旋弹簧，来代替，而将弹簧特性设为油气弹簧特性。其一端连接于下横臂上，另一端连接车身。由于使用了特殊的油气弹簧结构，可以将车轮位置根据行驶需要来主动调节，实现轮胎的收放。其前减震器的安装角为15.1º。

4、仿真分析

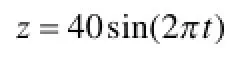
、变异概率Pm =0.01时，悬架性能较好。因ADAMS软件内部不存在程序设计及优化辅助分析的设置，故本文采用MATLAB语言编写了小生境遗传算法优化程序, 建立数学模型，通过约30代迭代，得最优的10组解，并分析各解的机构模型，排除运动干涉解，从而得到最优解。模型的仿真分析结果如图7-10所示。

从优化后的结果可以看出，主销内倾角实际设计时，大致范围为：7°～13°，希望取较小的数值，本文所得角度为7.5°。主销后倾角一般认为0°～ 10°是合理的范围，本文取 9.7°。当车轮跳动过程中，外倾角变化为-2°～-0.5° /50mm。而且前轮的前束角变化范围为0～1°/50mm，变化范围合理且幅度较小，满足设计要求。故优化后的各参数值的变化范围较为理想，且在满足两栖车收放功能的前提下，机构有良好的运动特性。

5、结论

本文利用小生境遗传算法和并列选择法，结合两者优点对某水陆两栖车的车轮收放装置，即改进型双横臂独立悬架进行了运动学多目标优化设计计算，通过高次迭代后，排除干涉解，取得了全局最优解，并结合多体系统动力学，利用ADAMS软件，通过仿真，验证两栖车收放装置的运动特性。结果表明，利用小生境遗传算法可以进行复杂空间系统的结构参数优化设计，并获得悬架系统的有效设计方法。

[1] 徐一新,李书伟王琪等.基于组合建模法的两栖车辆车体优化分析[J].计算机仿真，2013（03）：173-176，183.

[2] 剧冬梅,李军.轮式两栖车辆关键技术研究[J].汽车运用，2013（05）：5-6.

[3] Gary M Gere,Russell L Holder,Louis J Musetti,Ray Ramsey.Amphi -bious vehicle:USA, 444829 [P].1995-05-18.

[4] Alan Timothy Gibbs.Amphibious vehicle:GB,134953.11[P].2005 (05)：23.

[5] 丁飞,韩旭,刘桂萍等.悬架导向机构硬点灵敏度分析及多目标优化设计[J].汽车工程,2010，32(2):137-142.

[6] 施睿,赵春霞.双横臂独立悬架运动学分析与优化设计[J].车辆与动力技术,2014（03）:35-41.

[7] 杨波,左曙光,覃霍,韩乐.双横臂独立悬架导向机构硬点匹配设计[J].机械设计与制造,2010（10）：65-67.

[8] 陈加国,宗亚平.双横臂独立悬架运动特性仿真与分析[J].汽车零部件,2013（ 8）：86-88.

[9] 潘国昌,黄虎,刘新田,刘长虹.双横臂独立悬架运动学仿真分析[J].机械设计与制造,2009（11）：200-202.

[10] 陈黎卿，陈无畏，何钦章.双横臂扭杆独立悬架多目标遗传优化设计[J].中国机械工程学报，2007，18(17)：2022-2025.

[11] 陈羽,刘江南,韩旭等.双横臂式前独立悬架的改进遗传算法优化[J].中国机械工程学报,2007，18(22)：2756-2759.

[12] JASZKIEWICZ A. Genetic local search for multi-objective combin -atorial optimization [J]. European Journal of Operational Research, 2002(01):50-71.

[13] 舒勇.ADAMS在汽车双横臂独立悬架运动特性分析中的应用[J].汽车实用技术,2013（05）:16-19.

[14] 张亮亮,裴永生,吴丹丹.基于 ADAMS的双横臂独立悬架的仿真分析及优化设计[J].现代机械,2010(04):27-29.

[15] Cavicchio D J.Reproductive Adaptive Search Using Simulated Evolution [D].Ann Arbor,USA:University of Michigan,1970.

[16] 武兴亮,丁根宏.改进小生境遗传算法求解多峰函数优化问题[J].信息技术,2013（1）：73-76.

The Optimization Design of the Wheel’s Retracted and Amphibious Vehicle Using Niche Genetic Algorithm

Bao Zhenming1, Wang Qi2, Xu Yixin2, Tang Su2
( 1. Dynamic, Jiangsu University of Science and Technology, Jiangsu Zhenjiang 212003;
2. Mechanical Engineering, Jiangsu University of Science and Technology, Jiangsu Zhenjiang 212003 )

The statics model and dynamics model for the improved-double-wishbone independent suspension guide mechanism and deployed for the amphibious vehicle are established, according to the characteristics of device’s retracted. Using the niche genetic algorithm, a multi-objective optimization program in MATLAB to verify the feasibility of the solution after the high iteration. Tthe global optimal solution was obtained. A kinematics model in ADAMS is made. The results achieved the design performance index of the suspension. An effective method to design the suspension system obtained.

Amphibious vehicle; Double-wishbone independent suspension; Retracted and deployed Device; NGA

U463

A

1671-7988（2015）09-41-05

包振明，就职于江苏科技大学，研究方向为轮机工程。

国家自然科学基金项目（61105071）和江苏省产学研前瞻性联合研究项目（BY2012179）的资助。