色关联随机力作用下吸积盘振荡光度的功率密度谱

陈培杰，蒋亚玲，汪志云



色关联随机力作用下吸积盘振荡光度的功率密度谱

陈培杰，蒋亚玲，汪志云

(湖北文理学院物理与电子工程学院，湖北襄阳441053)

采用受色关联随机力作用下的广义朗之万方程描述黑洞吸积盘的垂向振荡，推导得到吸积盘随机振荡的光度和功率密度谱，并分析了黑洞双星系统参数对功率谱曲线的影响. 研究结果表明：当选取适当系统参数时，功率密度谱曲线上会出现随机共振现象；随机力的关联时间、吸积盘的吸积率和粘滞系数决定随机共振强弱，但共振峰位置只随黑洞质量不同而发生变化．

色关联随机力；广义朗之万方程；吸积盘；功率密度谱；随机共振

在天体物理中，黑洞和中子星等致密天体都包围有一个吸积盘，吸积盘物理模型也被用来解释X射线黑洞双星的一些观测数据. 近年来，许多学者研究了受随机力作用的吸积盘的振荡，并取得较大成功. 吸积盘的随机力主要由外部作用产生(如潮汐或者冲击波扰动等)，也可能是湍流动力学方程中被忽略的非线性项. Ioannou 和 Kakouris等人研究了二维开普勒吸积盘随机动力学，并计算了在空间和时间白随机力作用下，吸积盘的结构和角动量向外转移，发现如果力是宽波段且足够大，向中心天体的吸积能够被随机力维持[1]；Harko 和 Mocanu等人推导在广义相对论框架下，受随机力作用的超大质量黑洞吸积盘扰动的垂向振荡方程，通过数值模拟得到了吸积盘垂向振荡的位移、速度和光度，并分析了功率密度谱随频率的变化[2]；Leung 等人研究了围绕大质量黑洞吸积盘的垂向扰动随机振荡，发现Blacc天体24h内光度变化与吸积盘的随机振荡有关[3].

以上研究表明，吸积盘随机振荡的光度及其功率密度谱与观测到的光变现象基本吻合，一些观测现象可以用吸积盘随机振荡解释. 分析非相对论情况下流体吸积盘和广义相对论盘随机振荡光度的功率密度谱时，发现存在随机共振现象，并解释了黑洞双星Ｘ射线的低频准周期振荡现象[4-5]. 但以上讨论所采用的随机力都是白噪声型，事实上随机力还可能存在指数形式色关联型．如Leung 等人用数值模拟方法得到色关联随机力作用下吸积盘振荡的光变曲线[6]. 本文主要用色关联随机力作用下的广义朗之万方程描述吸积盘振荡，从理论上计算其随机振荡的光度和功率密度谱，分析吸积盘系统参数对功率密度谱曲线随机共振的影响．

1　色噪声作用下吸积盘振荡的功率密度谱

考虑标准吸积薄盘，将吸积盘作为整体，受随机力作用产生振荡，其垂向振荡方程为[3]：

式中，M是吸积盘质量，是吸积盘的垂向振荡位移，是吸积盘受到的粘滞作用系数，可以看成常量.()是随时间变化的色关联随机力，其平均值和在不同时间和的关联满足以下统计性质：

式中，和为常数，表示随机力作用强度，表示随机力关联时间. 令，，，则式(1)变为：

速度为

吸积盘振荡的总能量可以表示为：

吸积盘的光度是由于粘滞耗散导致的盘振荡能量的损失，由式(3)和(6)可得到光度为[2]：

由方程(7)得到吸积盘振荡光度的自相关联函数为：

将方程(2)、(5)代入式(8)可得

其中：

对式(9)平均光度自相关函数进行傅立叶变换，得光度的功率密度谱为：

对于一个包围黑洞或中子星的流体吸积薄盘，假定吸积盘的密度分布满足以下关系[7-8]：

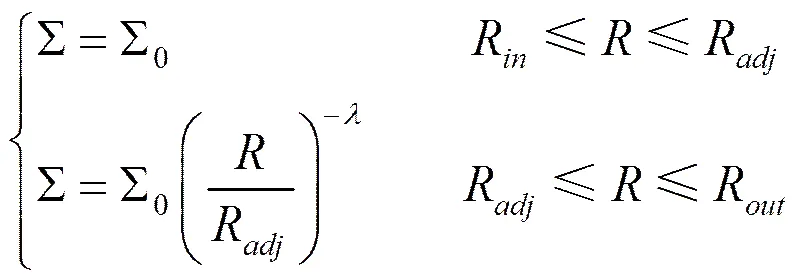
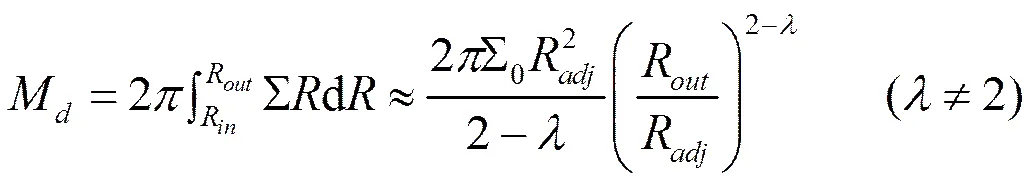
其中，、分别为粘滞系数和以临界吸积为单位的吸积率，根据文献[3]吸积盘振荡的粘滞阻尼系数和固有频率分别为：

2　系统参数对功率密度谱的影响

将式(10)、(13)和(14)代入方程(11)，得到黑洞双星系统的吸积盘随机振荡的光度功率密度谱随频率变化关系. 假设吸积盘面密度指数，调整半径为、外半径为，当其它参数分别取不同值时，吸积盘随机振动光度的功密度谱曲线如图１所示.

可以看出：吸积盘随机振荡光度的功率密度谱曲线出现一截断，将其大致分为斜率不相同的两部分；并且所选参数合适时，在高于截断频率部分，功率密度并不随频率单调减小，而是出现一峰值，即出现随机共振现象.

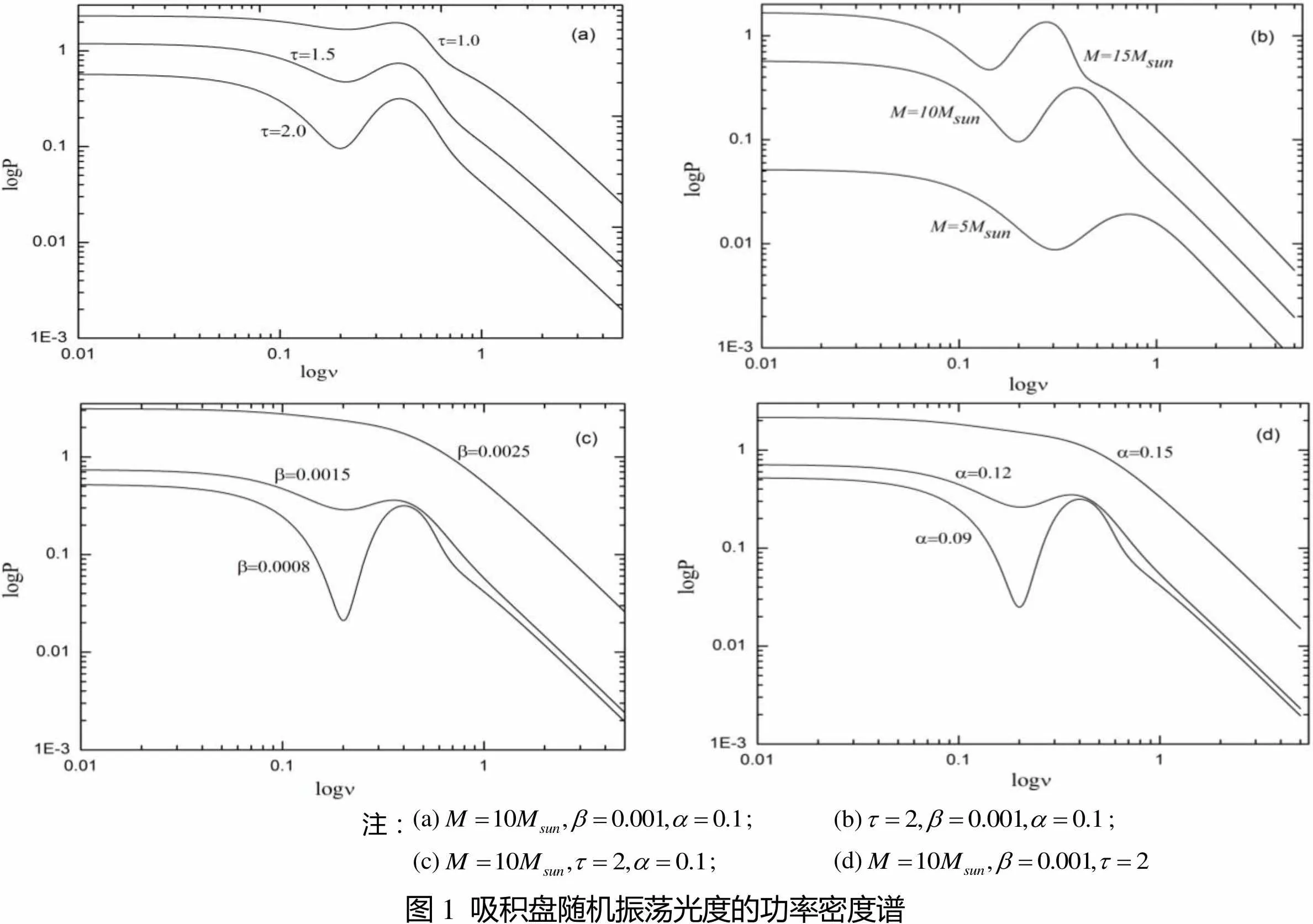
注：(a); (b); (c);(d) 图1吸积盘随机振荡光度的功率密度谱

图1(a)表示是随机力关联时间不同时，吸积盘随机振荡的功率密度谱．可以发现：增大时，谱线整体下移，曲线的共振峰越高，越尖锐，共振现象越明显，共振峰值所对应的频率几乎不变；而当减小时，共振现象会逐渐减弱. 吸积盘中心黑洞的质量对功率密度谱的影响主要表现在对共振峰出现的位置(如图１(b)所示)，不同，谱线的轮廓并没有发生明显变化，即不影响随机共振现象，但是很显然，越大，共振峰对应的频率越低；由图１(c)和(d)可知：吸积盘的吸积率和粘滞系数对功率密度谱的影响完全相同，共振峰的变化对它们的取值敏感. 随着取值增大时，共振迅速减弱，直至消失，但出现共振峰的位置并不发生变化．而且和对于共振峰右侧部分的功率密度谱影响较小，而对左侧部分影响较大．

由方程(12)、(13)和(14)可知，吸积率和粘滞系数影响吸积盘的粘滞耗散系数，不影响吸积盘随机振荡的固有频率．即和增大，增大，不变，吸积盘的粘滞作用越强，耗散能量增多，光度越强，此时随机力的作用相对较弱，不容易形成随机共振现象．当粘滞作用较小时，随机力使功率密度在一定的频率范围内增大，出现随机共振现象．吸积盘中心黑洞的质量不同，只改变固有频率，不改变，这说明吸积盘的垂向振荡频率越高，功率密度谱曲线的共振峰对应的频率越高．由方程(7)可知，吸积盘垂向振荡产生的光度主要由粘滞产热和随机力做功所产生的. 当粘滞作用和吸积盘振荡的固有频率满足一定的条件时，吸积盘损失能量(即产生的光度)的功率随频率的变化由于共振而出现准周期性振荡.

3　结语

通过以上分析可得到：受指数形式色关联随机力作用，黑洞吸积盘系统随机振荡光度的功率密度谱(曲线)主要是由斜率不相同的两部分组成，并且出现随机共振现象. 随机力的关联时间、吸积盘吸积率和粘滞系数决定吸积盘的粘滞耗散能量，影响随机共振的强弱. 而黑洞的质量通过改变吸积盘振荡的固有频率而影响共振峰所在位置．吸积盘随机振荡光度的功率密度谱曲线与黑洞双星系统观测的X射线光变曲线有相同轮廓[9-10]．特别是在功率密度谱曲线出现的随机共振峰类似于观测的准周期振荡．而黑洞双星观测的X射线功率密度谱的准周期振荡产生的物理机制一直是很不清楚的．本文研究认为引起0.01—1Hz范围内的低频准周期振荡原因可能是由随机力、中心天体引力和粘滞力作用下的吸积盘随机共振引起．

[1] IOANNOU P J, KAKOURIS A. Stochastic dynamics of keplerian accretion disks[J]. The Astrophysical Journal, 2001, 550(4): 931-943.

[2] HARKO T, MOCANU G. Stochastic oscillations of general relativistic disks[J]., 2012, 421(4): 3102-3110.

[3] LEUNG C S, WEI J Y, HARKO T, et alModeling the IDV emissions of the BL Lac objects with a Langevin type stochastic differential equation[J].,2011, 32(1-2): 189-192.

[4]WANG Z Y, CHEN P J, WANG D X, et alStochastic resonance of accretion disk and the persistent low-frequency quasi-periodic oscillations in black hole X-ray binaries[J]. JAA, 2013, 34(1): 33-40.

[5] WANG Z Y, CHEN P J, ZHANG L Y. Stochastic resonance of a general relativistic accretion disk[J]. CHIN. PHYS. LETT., 2013, 30(9): 1-4

[6] LEUNG C S, MOCANU G, HARKO T. Generalized langevin equation description of the stochastic oscillations of general relativistic disks[J]. J. Astrophys.Astr., 2013(6): 1-17.

[7] TITARCHUK L, OSHEROVICH V. The global normal disk oscillations and the persistent low-frequency quasi-periodic oscillations in X-ray binaries[J]. The Astrophysical Journal, 2000, 542(2): 111-114.

[8] SHAKURA N I, SUNYAEV R A. Black holes in binary systems: Observational appearance[J].1973, 24: 337-355.

[9] REMILLARD R A, MCCLINTOC J E. X-Ray properties of blackholebinaries[J].2006, 44(1): 49-92.

[10] MCCLINTOC J E, REMILLARD R A. Black Hole Binaries[M]. Cambridge: Cambridge Univ. Press, 2006.

Power Spectral Density of Oscillating Luminosity for Accretion Disk Driven by Stochastic Force with Color Correlation

CHEN Peijie, JIANG Yaling, WANG Zhiyun

(School of Physics and Electronic Engineering, Hubei University of Arts and Science, Xiangyang 441053, China)

A generalized Langevin type equation driven by stochastic force with color correlation is used to describe the stochastic oscillations on the vertical direction of the accretion disk around black hole, the luminosity and the power spectral density for oscillating disk are calculated. Then the influences of parameters on the curves are discussed. The results show that,when all parameters of system take appropriate values, the stochastic resonance phenomenon is found in power spectral density curves; The correlated time of stochastic force, mass accretion rateand viscidity coefficientaffect the strength of stochastic resonance, and the position of resonance peak is changed with variety of the mass of black hole.

Stochastic force with color correlation; Generalized Langevin equation; Accretion disks; Power spectral density; Stochastic resonance

(责任编辑：饶 超)

P145. 8

A

2095-4476(2015)02-0005-04

2014-10-27

湖北省教育厅重点研究项目(D20132603)

陈培杰(1975— ), 女, 湖北枣阳人, 湖北文理学院物理与电子工程学院副教授.