带积分边界条件的非线性高阶分数阶微分方程解的存在性
2015-10-14武竞力杨喜陶
武竞力, 杨喜陶
带积分边界条件的非线性高阶分数阶微分方程解的存在性
武竞力, 杨喜陶
(湖南科技大学数学与计算科学学院, 湖南湘潭, 411201)
首先通过拉普拉斯变换得出一类带积分边界条件的非线性高阶分数阶微分方程满足边界条件的解, 再利用压缩映射原理和Krasnosel’skii不动点理论, 讨论了这类方程解的存在性和惟一性。
分数阶微分方程; 边界值问题; 压缩映射原理; 不动点理论
分数阶微积分涉及到将整数阶导数和积分推广到任意阶, 在最近40年引起了极大关注。随着分数阶微积分理论的发展, 分数阶微分方程被广泛应用于科学和工程领域[1-7]。近年来, 带积分边界条件的分数阶微分方程的解问题被普遍研究, 而且在实际应用中有很大价值。
考虑带一个积分边界条件的分数阶微分方程:
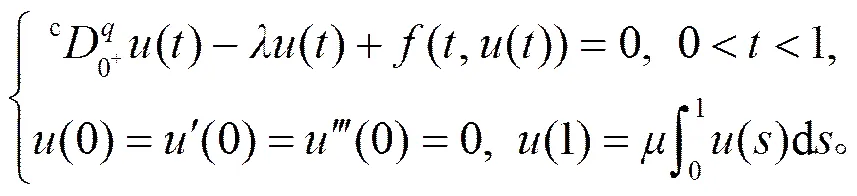
1 几个引理
考虑下面一个边界值问题:


运用另一个边界条件, 有
。 (4)
对式(3)两边同时从0到1积分, 得到

。 (5)

将式(6)代入式(3), 得到问题(2)的解

引理2 (压缩映射原理[10]) 设是一个Banach空间,是的闭子集,是一个严格压缩映射, 即对任意不等式成立, 其中。那么有惟一一个不动点。
引理3 (Arzela-Ascoli[10]) 如果的一个紧子集中的点列是一致有界和等度连续的, 则它有一个一致收敛的子列。
引理4(Krasnosel’skii[11]) 设是一个Banach空间,是的一个凸的非空闭子集,和是2个算子, 使得: (1) 对任意(2)是紧的和连续的; (3)是压缩映射。那么存在一个, 使得。
2 主要结论
应用上面的引理, 可以得到2个定理。





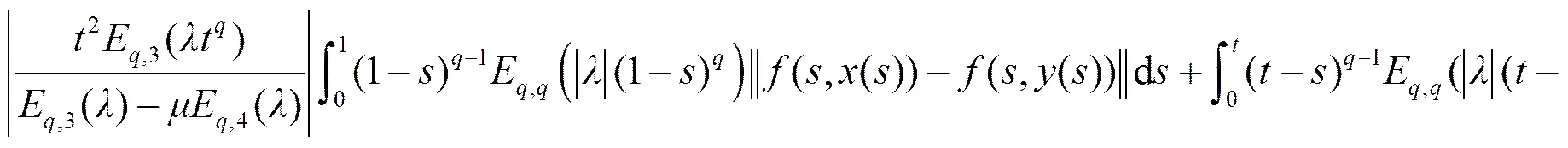
。

举例:
例1 考虑边界值问题

例2 考虑边界值问题

参考文献:
[1] Mainardi F. The fundamental solutions for the fractional diffusion-wave equation [J]. Applied Mathematics Letters, 1996, 9(6): 23-28.
[2] Buckwar E, Luchko Y. Invariance of a partial differential equation of fractional order under the Lie group of scaling transformations [J]. Joural of Mathematical Analysis and Applications, 1998, 227(1): 81-97.
[3] Zhu Z Y, Li G G, Cheng C J. Quasi-static and dynamical analysis for viscoelastic Timoshenko beam with fractional derivative constitutive relation[J]. Applied Mahematics and Mechanics, 2002, 23(1): 1-12.
[4] Agrawal O P. Some generalized fractional calculus operators and their applications in integral equations [J]. Fractional Calculus and Applied Analysis, 2012, 15(4): 700-711.
[5] Zhang Y, Hou C M. On discrete sequential fractional boundary value problem with fractional boundary conditions [J]. Annals of Differential Equations, 2013, 29(3): 369-378.
[6] Lv Z M, Gong Y P, Chen Y. Multiplicity and uniqueness for a class of discrete fractional boundary value problems [J]. Applications of Mathematics, 2014, 59(6): 673-695.
[7] Graef John R, Kong L J. Existence of positive solutions to a higher order singular boundary value problem with fractional q-derivatives [J]. Fractional Calculus and Applied Analysis, 2013, 16(3): 695-708.
[8] Xu Y F, He Z M. Existence of solutions for nonlinear high-order fractional boundary value problem with integral boundary condition [J]. Journal of Applied Mathematics and Computing, 2014, 44(1): 417-435.
[9] Podlubny I. Fractional Differential Equations [M]. New York: Academic Press, 1999: 103-109.
[10] Deimling K. Nonlinear Functional Analysis [M]. Berlin: Springer, 1985: 35.
[11] Smart D R. Fixed Point Theorems [M]. Cambridge: Cambridge University Press, 1980: 213.
(责任编校:刘晓霞)
Existence of solutions for nonlinear high-order fractional boundary value problem with integral boundary condition
Wu Jingli, Yang Xitao
(School of Mathematics, Hunan University of Science and Technology, Xiangtan411201, China)
The existence of solutions of a class of nonlinear high-order fractional differential equations with integral boundary conditions is studied. By using Laplace transform, the contraction mapping principle and Krasnosel’skii fixed point theorem, the existence and uniqueness of solution are obtained, which enriches the theory for the solution of fractional differential equations.
fractional differential equations; boundary value problem; contraction mapping principle; fixed point theorem
10.3969/j.issn.1672–6146.2015.03.001
O 175.6
1672–6146(2015)03–0001–05
武竞力, beckhsm7777777@sina.com。
2015–03–13
湖南省自然科学基金项目(2015JJ2063); 湖南科技大学研究生创新基金项目(S140035)。
