基于到达时间差直方图的信号分选算法研究

杨 翔 顾洪宇



基于到达时间差直方图的信号分选算法研究

杨 翔 顾洪宇

(中航工业雷华电子技术研究所北京创新中心 北京 100012)(航空电子系统射频综合仿真航空科技重点实验室 无锡 214063)

到达时间差(TDOA)直方图分析是电子支援侦察雷达信号主分选的基础；相关信号分选算法的性能与TDOA直方图脉冲重复间隔(PRI)检测门限的设定密切相关。为揭示PRI检测门限与TDOA直方图参数之间的关系，解决传统PRI检测门限依靠经验设定、无法灵活调整的问题，该文从分析TDOA直方图与脉冲序列的统计性质入手，推导了直方图稳定PRI、抖动PRI和参差PRI检测门限的解析表达式，提出了基于TDOA直方图PRI检测的信号分选算法，并通过仿真验证了算法的有效性。

信号处理；信号主分选；到达时间差直方图；脉冲重复间隔检测门限

1 引言

信号分选是电子侦察信号处理的核心，它利用雷达侦察接收机侦测到的脉冲信息(如到达角度、到达时间、载频、脉宽和幅度等)将由不同辐射源辐射、在时间上相互交叠的脉冲序列分离开，为判断辐射源类别、工作模式和威胁程度提供信息。

信号分选通常分为预分选、主分选和扫描分析3部分[1]，分别完成脉冲流稀释、脉冲重复间隔(Pulse Repetition Interval, PRI)检测与脉冲抽取，以及雷达扫描方式分析。其中，信号主分选是信号分选领域的热点和难点[2]。从上世纪80年代开始，各种信号分选方法相继出现[3]。主要算法包括基于到达时间差(Time Difference Of Arrival, TDOA)直方图的算法和变换域分析方法。

基于TDOA直方图的算法包括TDOA直方图算法、累积TDOA直方图算法(Cumulative Difference Histogram, CDIF)[4]、序列差直方图算法(Sequence Difference Histogram, SDIF)[5]、PRI变换法[6]等。这些算法利用脉冲序列间TDOA的统计特性检测辐射源PRI，进而完成脉冲抽取。

变换域分析法包括谱估计法[7]和平面变换法[8]，主要利用脉冲到达时间规律检测辐射源PRI，进而完成脉冲抽取。基于TDOA直方图的算法和变换域分析方法分别适用于低脉冲密度/高重频环境下的PRI检测和高脉冲密度/低重频环境下的PRI检测[9]，在实际系统中经常搭配使用[10]。此外，近年来，出现了基于聚类/人工智能和脉内特征参数的信号分选算法[11]，这些算法充分借鉴了其他领域的研究成果，对复杂电磁环境下的雷达信号分选具有较好的应用前景[12]，但实用性仍有待提升。

本文针对TDOA直方图信号分选算法开展研究。与前人将研究重点放在降低计算复杂度[4,5]和PRI谐波滤除不同[6]，本文从TDOA直方图的基本性质入手，先后推导了具有稳定PRI、抖动PRI和参差PRI的TDOA直方图检测门限的解析表达式，从而揭示了各类PRI检测门限与TDOA直方图参数之间的内在联系。在此基础上，本文进一步给出了一种基于TDOA直方图的信号分选算法，并通过仿真验证了所提出算法的有效性。值得一提的是，本文推导的TDOA直方图PRI检测门限可进一步推广至CDIF算法和PRI变换法。

本文余下部分安排如下：第2节简要回顾TDOA直方图与TOA序列自相关函数的关系；第3节推导稳定、抖动和参差PRI脉冲串TDOA直方图的解析表达式，并据此设定PRI检测门限；第4节给出基于TDOA直方图的信号分选算法；第5节中对理论推导结果和提出的信号分选算法的进行仿真验证；最后对本文进行总结。

2 TDOA直方图与TOA序列自相关函数

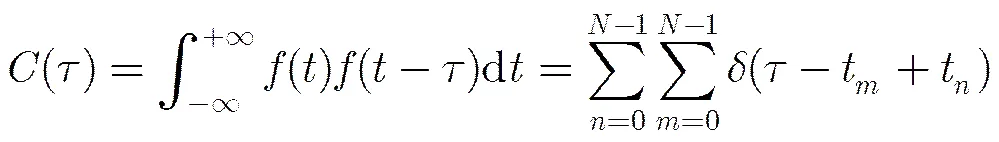
3 TDOA直方图PRI检测门限

本节依次考虑稳定、抖动和参差PRI脉冲串，推导TDOA直方图解析表达式，并在此基础上给出PRI检测门限。

3.1 稳定PRI脉冲串

利用第2节的推导方法，可以得到稳定PRI脉冲串TOA序列的直方图表达式：

在推导完稳定PRI TOA序列的TDOA直方图后，下面考虑TDOA直方图中稳定PRI检测门限设定问题。因为在实际分选过程中，无法预知辐射源辐射脉冲的数目和所使用的PRI，所以需要基于观测时长以及直方图参数(如箱长)来设定PRI检测门限。

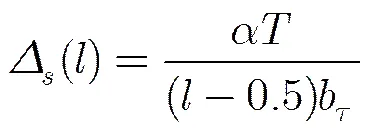
3.2抖动PRI脉冲串

同样利用第2节的推导方法，可以得到抖动PRI脉冲串TOA序列的直方图表达式：

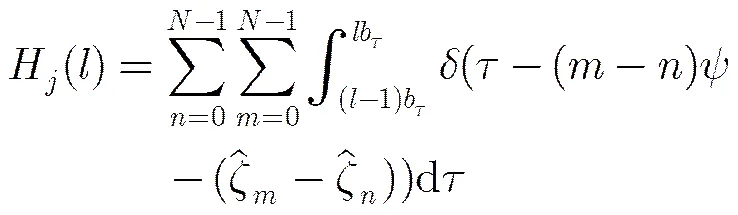
其中

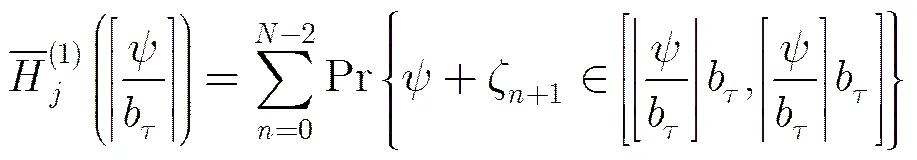
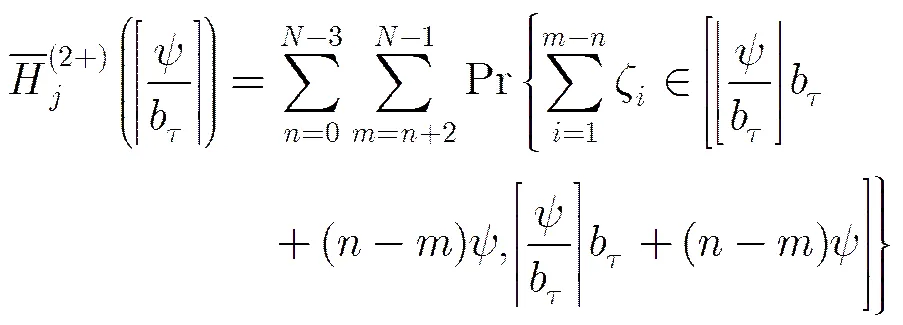
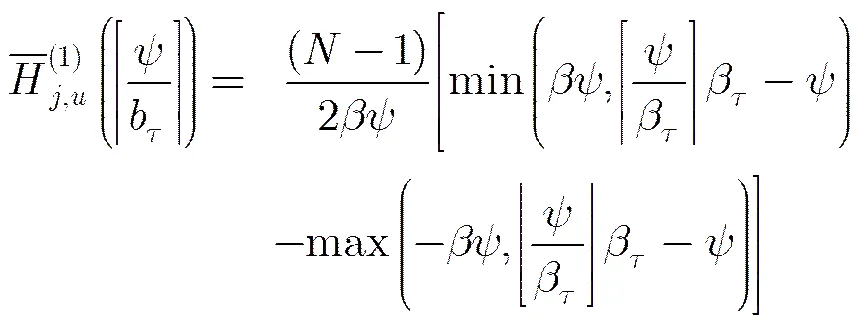
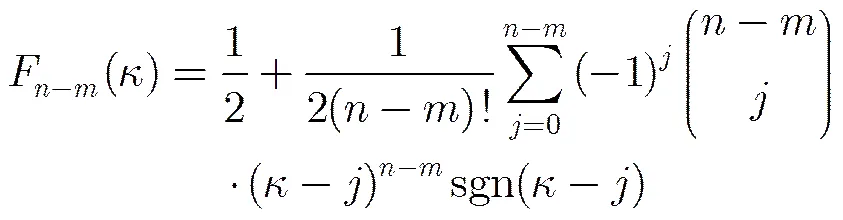
将式(12)代入式(11)，计算整理可得

在推导出PRI均值处TDOA直方图幅度期望值后，下面推导PRI均值检测门限。与3.1节相同，这里引入因子，考虑的情况，则式(14)可进一步写为

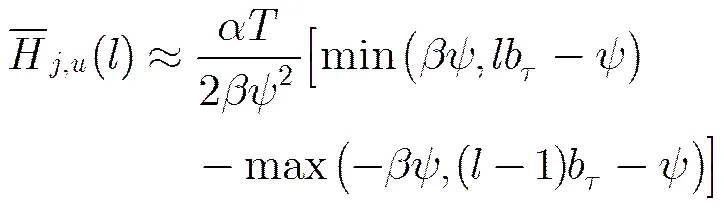
3.2.2正态分布情况 下面考虑PRI抖动服从正态分布的情况，假设，并用表示PRI抖动服从正态分布时的取值。

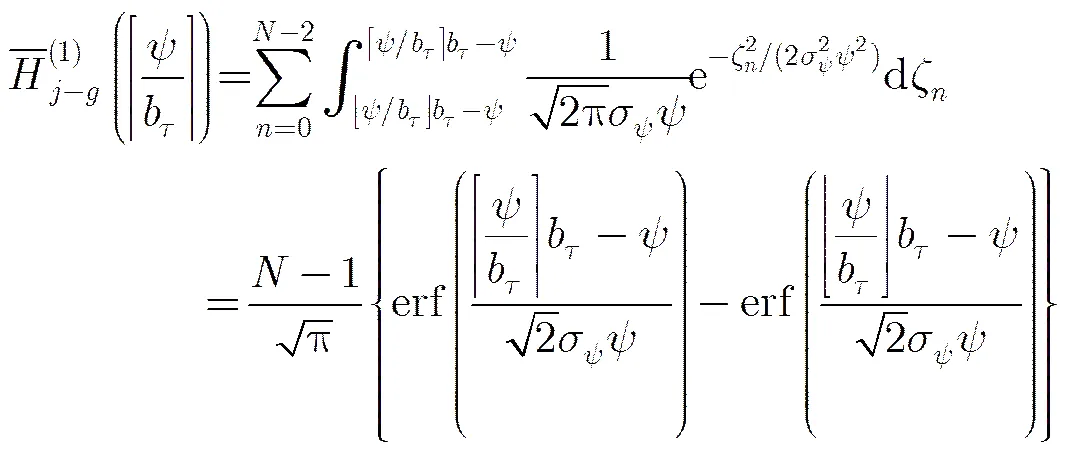
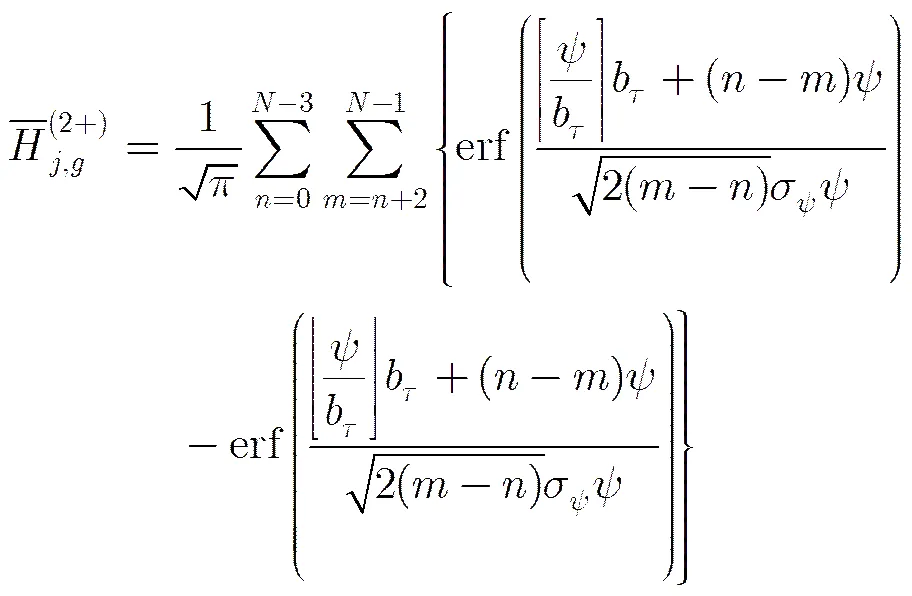
其数值计算结果与PRI抖动服从均匀分布的情况相同，也趋近于零。

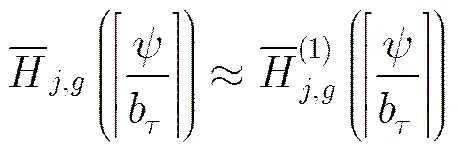
3.3参差PRI脉冲串

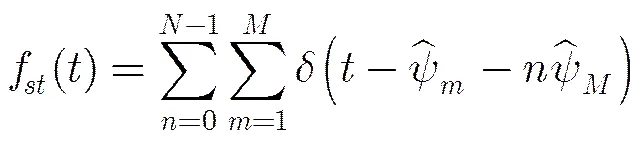
参差PRI脉冲串的TDOA直方图可以表示为

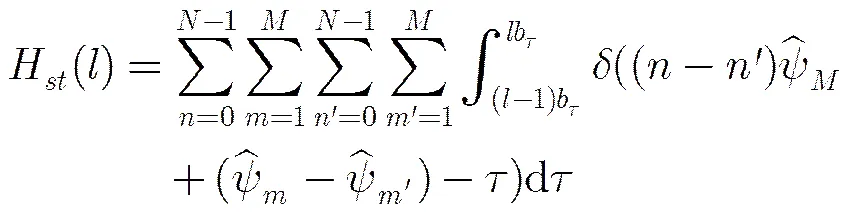
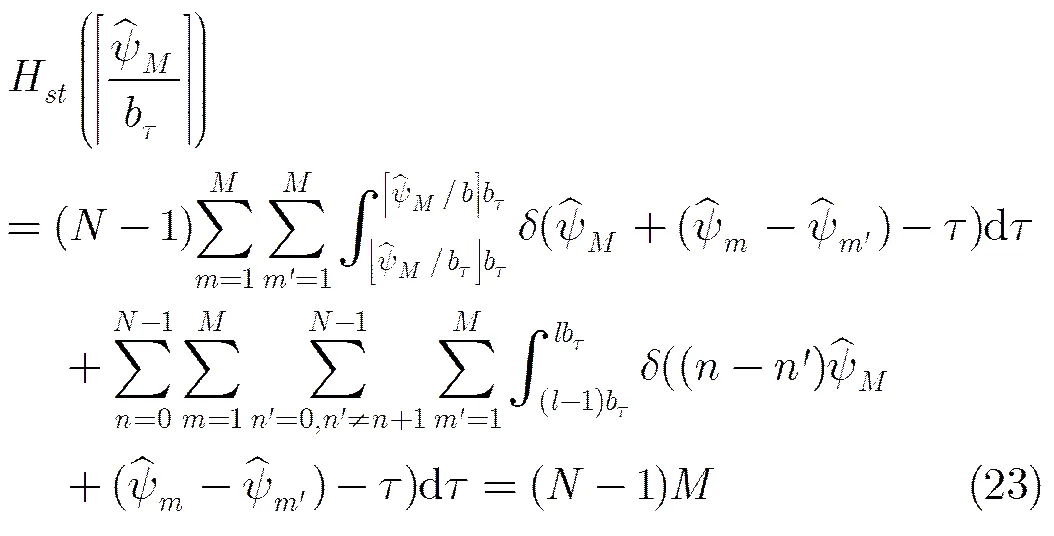
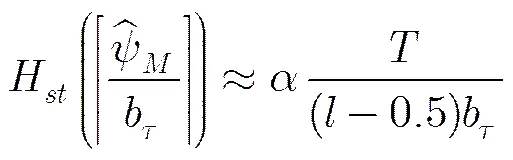
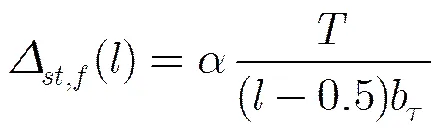
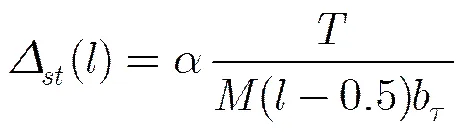
比较式(5)，式(25)和式(26)可知，参差PRI骨架周期与稳定PRI具有相同的检测门限。因此，在实际检测过程中，参差PRI很有可能会被误检为稳定PRI，需要在后期通过参差PRI检验进一步从多个稳定PRI脉冲串中识别和提取参差PRI脉冲串。

4 基于TOA直方图分析的信号分选算法

在第3节的基础上，本节针对实际应用场景中存在大量具有不同PRI模式的TOA混合序列，提出基于TDOA直方图的信号分选算法。

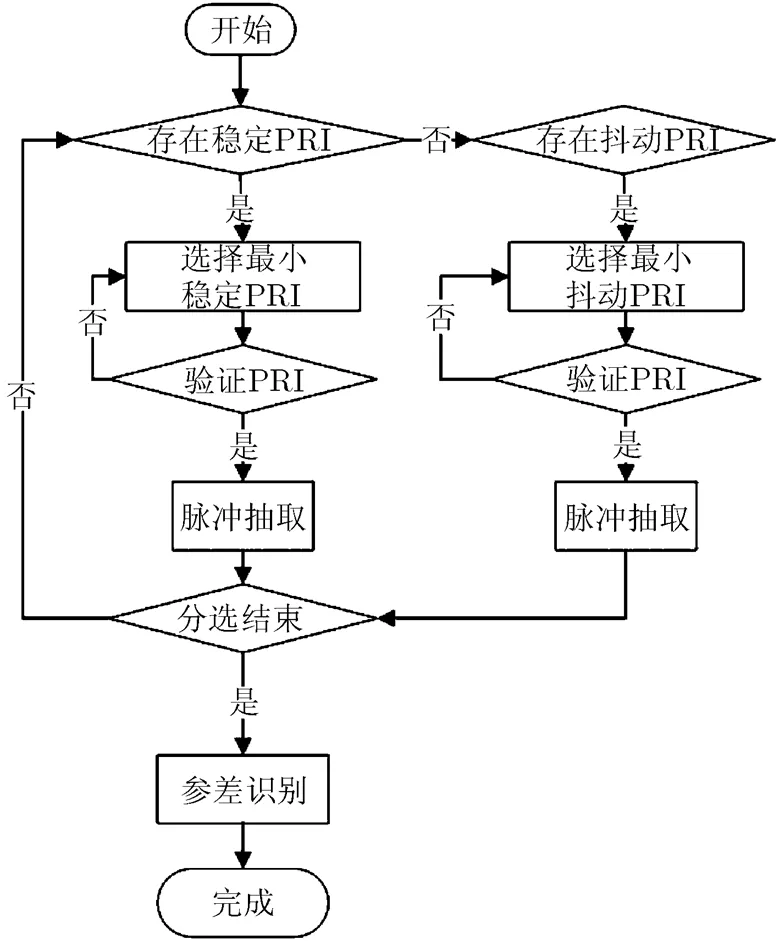
图1 混合PRI检测流程

算法的基本框架见图1。由于混合脉冲序列中的PRI类型未知，所以分别需要利用稳定PRI门限值与抖动PRI门限值来判断当前序列中是否存在稳定PRI与抖动PRI。对于稳定PRI和抖动PRI，其检测流程分为3部分：PRI检测、PRI确认和脉冲抽取。其中，PRI检测是指对于直方图统计结果，将超过门限值所对应的时间变量取为PRI候选值，具体来讲，首先利用门限式(5)，若有统计值超过该门限，则认为当前序列中存在稳定PRI；否则，利用门限式(17)，若有统计值超过该门限，则认为当前序列中存在抖动PRI。对于抖动PRI，还需要通过直方图抖动的展宽估计PRI参数，即对于超过直方图检测阈值的统计值，利用其对应的直方图旁瓣宽度估计PRI的抖动范围，并利用统计平均值估计PRI中心值(采用联通加权策略，详见文献[14])；PRI确认是指对检测到的PRI候选解进行检验，判断其是否为真实的PRI值，PRI确认采用文献[15]中的方法，即通过设定一个容差，并以任意一个脉冲为起始脉冲，以检测到的PRI为步长，若能连续检测到5个脉冲，则认为该候选PRI为真实的PRI。这里的容差是指取值的变化范围，对于稳定PRI和参差PRI，确定PRI时的容差等于检测直方图的箱长；对于抖动PRI，确定PRI时的容差等于检测直方图的箱长与抖动范围值之和；脉冲抽取是指利用PRI确认后通过验证的PRI值，提取出其对应的脉冲序列。

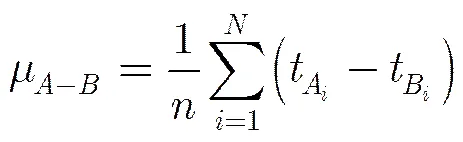
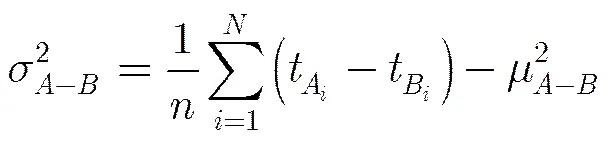
参差识别完成后，整个混合PRI的检测流程结束。

5 仿真验证

本节将通过仿真对上文推导的PRI检测门限和提出的信号分选算法进行验证。所有仿真实验中的观测时长都设定为，门限函数的系数设定为，直方图箱数设定为，直方图箱长设定为。

为验证PRI检测门限，我们选取了4个典型的脉冲串，详见表1。图2给出了仿真结果，可以看出利用理论推导结果设定的门限函数满足检测需求。同时，对于稳定PRI和抖动PRI，其TDOA直方图统计结果中的基波成分与谐波成分都会超过门限，这就要求在检测稳定PRI与抖动PRI时，需要引入子谐波验证的操作，具体方法为：对于超过门限的统计值，由小到大遍历其对应时间变量的正约数，若有正约数处的直方图统计值超过当前门限值，则认为当前检测到的PRI为子谐波成分，而其正约数处为基波成分；对于参差PRI，其TDOA直方图统计结果中会由于子参差PRI的互相关产生互相关峰值，即对于子参差PRI为的参差PRI，子参差PRI间的互相关会导致直方图统计结果在,,等处产生峰值。

表1 PRI门限验证的辐射源数据信息表

图2 PRI检测门限验证

图3 多模式PRI检测

表2多模式PRI检测的分选结果统计

雷达类型PRI取值脉冲个数PRI测定值分选出脉冲个数正确分选个数准确率(%) 稳定21513921514013899.28 抖动18016918015014887.57 参差213,237,252123213,237,25212512299.19

为了验证基于TDOA直方图的信号分选算法的性能。实验选取了3种典型的脉冲序列，见表2，其中，抖动PRI的抖动值服从均匀分布且抖动范围为中心PRI值的(-10%,10%)，图3给出了仿真图，表2给出了仿真统计结果。由仿真结果可以看出，本文算法可以有效检测和抽取稳定PRI和参差PRI脉冲序列，准确率分别为99.28%和99.19%，对于抖动PRI脉冲序列，本算法的分选正确率也达到87.57%。影响抖动脉冲序列分选结果的主要原因有两点：(1)由于先进行稳定PRI和参差PRI的剔除，后进行参差PRI的检测，因此未能完全剔除掉的属于稳定PRI或参差PRI的脉冲对于后续的抖动PRI检测为干扰脉冲，同时，被错误剔除掉的本属于抖动PRI的脉冲对于后续抖动PRI的检测为丢失脉冲，干扰脉冲和丢失脉冲的存在会影响对抖动PRI的分选；(2)由于抖动的影响，为了保证算法性能，在进行抖动PRI序列剔除时需要设定大的容差值，而容差过大会导致将错误脉冲套取到当前序列中，进而影响到后续的序列剔除操作。这是因为在进行序列检测与剔除时，如果在容差范围内出现多于一个的候选脉冲时，算法会选取最接近容差范围中心的脉冲作为最优解，然而这种选择方式得到的仅仅是当前最优解，容差越大，以这种选择方式得到的当前最优解越多，会造成序列检测时的误差积累，最终导致检测错误。解决第(1)种问题的方法之一是对不同模式的PRI分选时采用不同的箱长，解决第(2)种问题的方法之一是对多个候选脉冲进行多假设跟踪，提高当前解最优的置信度。本文的后续研究将从这两点出发，以进一步提高TDOA直方图对抖动PRI的检测性能。

6 结束语

本文从具有各种PRI模式的脉冲串TDOA直方图推导入手，给出了TDOA直方图中各类PRI检测门限解析表达式，揭示了PRI检测门限与系统参数之间的关系。在此基础上，本文提出了基于TDOA直方图的信号分选算法，并通过实验进行仿真，验证了本文理论推导的正确性以及提出的脉冲分选算法的可行性。

[1] Wilkinson D R and Watson A W. Use of metric techniques in ESM data processing[J].,, 1985, 132(4): 229-232.

[2] 李英达, 肖立志. 一种脉冲重复间隔复杂调制雷达信号分选方法[J]. 电子与信息学报, 2013, 35(10): 2493-2497.

Li Ying-da and Xiao Li-zhi. A method of signal sorting for radar signal of pulse repetition interval complex modulated [J].&, 2013, 35(10): 2493-2497

[3] 杨学永, 宋国栋, 钱轶. 现代雷达信号分选跟踪的几种方法[J]. 现代雷达, 2014, 36(3): 43-48.

Yang Xue-yong, Song Guo-dong, and Qian Yi. A method of signal sorting for radar signal of pulse repetition interval complex modulated[J]., 2014, 36(3): 43-48.

[4] Mardia H K. New techniques for deinterleaving repetition sequences[J]., 1989, 136(4): 149-154.

[5] Milojevic D J and Popovic B M. Improved algorithm for deinterleaving of radar pulses[J]., 1992, 139(1): 98-104.

[6] Nishiguchi K and Kobayashi M. Improved algorithm for estimating pulse repetition[J]., 2000, 36(2): 407-421.

[7] Perkins J and Coat I. Pulse train deinterleaving via the hough transform[C]. Proceedings of IEEE Conference on Acoustics, Speech, and Signal Processing, Adelaide, 1994: 197-200.

[8] Orsi R J, Moore J B, and Mahony R E. Spectrum estimation of interleaved pulse trains[J]., 1999, 47(6): 1646-1653.

[9] 戴胜波, 雷武虎, 程艺喆, 等. 基于TOA分选的反电子侦察方法[J]. 电子信息对抗技术, 2014, 29(4): 45-48.

Dai Sheng-bo, Lei Wu-hu, Cheng Yi-zhe,. Electronic anti-reconnaissance based on TOA analysis[J]., 2014, 29(4): 45-48.

[10] Wang P C, Orr M, Sparrow M,. System and method for detecting and de-interleaving radar emitters[P]. US Patent, US007397415, 2008.

[11] 王世强, 张登福, 毕笃彦, 等. 基于快速支持向量聚类和相似熵的多参雷达信号分选方法[J]. 电子与信息学报, 2011, 33(11): 2735-2741.

Wang Shi-qiang, Zhang Deng-fu, Bi Du-yan,. Multi- parameter radar signal sorting method based on fast support vector clustering and similitude entropy[J].&, 2011, 33(11): 2735-2741.

[12] 杨承志, 肖卫华, 吴宏超, 等. 一种对多种重频调制类型雷达信号分选算法的研究[J]. 科学技术与工程, 2014, 14(34): 33-37.

Yang Cheng-zhi, Xiao Wei-hua, Wu Hong-chao,. Research on an improved sorting method for multiple PRI type radar signals[J]., 2014, 14(34): 33-37.

[13] The Irwin-Hall distribution[OL]. http://www.math.uah.edu /stat/special/IrwinHall.html, 2014.

[14] 陈维高, 张国毅. 基于直方图和脉冲关联的抖动信号分选算法[J]. 现代防御技术, 2014, 42(3): 142-148.

Chen Wei-gao and Zhang Guo-yi. Novel jitter signal sorting algorithm based on histogram and pulse associating[J]., 2014, 42(3): 142-148.

[15] 王石记, 司锡才. 雷达信号分选新算法研究[J]. 系统工程与电子技术, 2003, 25(9): 1079-1083.

Wang Shi-ji and Si Xi-cai. Research on an improved sorting method for radar signal[J]., 2003, 25(9): 1079-1083.

[16] 赵长虹, 赵国庆, 刘东霞. 对参差脉冲重复间隔脉冲列的重频分选[J]. 西安电子科技大学学报, 2003, 30(3): 381-385.

Zhao Chang-hong, Zhao Guo-qing, and Liu Dong-xia. The deinterleaving of radar pulse trains with stagger PRI[J]., 2003, 30(3): 381-385.

A Signal Sorting Algorithm Basedon Time Differenceof Arrival.Histogram

Yang Xiang Gu Hong-yu

((),,,100012,)(,214063,)

The Time Difference Of Arrival (TDOA) histogram is effective for pulse train de-interleaving in radar detection. The performance of TDOA-histogram based pulse sorting algorithm depends on several parameters in the histogram, such as the Pulse Repetition Interval (PRI) detection threshold and the box length, which are set posteriorly in traditional TDOA-histogram based algorithm. In this paper, the explicit expressions of detection threshold for various PRI modes (i.e. stable, jitter, and stagger) are derived, and the relationship among these parameters are revealed. Consequently, a signal sorting algorithm is proposed, and its performance is validated by simulation in complex signal environment.

Signal processing; Signal sorting; Time Difference Of Arrival (TDOA) histogram; Pulse Repetition Interval (PRI) detection threshold

TN971

A

1009-5896(2015)11-2762-07

10.11999/JEIT150209

2015-02-05；改回日期：2015-07-03；

2015-08-24

顾洪宇 guhy@ravic.cn

杨 翔： 女，1989 年生，助理工程师，研究方向为电子对抗.

顾洪宇： 男，1979年生，高级工程师，研究方向为低截获概率雷达、电子对抗.