基于蚁群算法的分布式卫星光网络波长路由分配技术研究

2015-10-14赵尚弘李勇军邓博于

电子与信息学报 2015年11期

董毅赵尚弘李勇军赵静邓博于

董毅*赵尚弘李勇军赵静邓博于

(空军工程大学信息与导航学院西安 710077)

为了解决分布式卫星光网络波长路由分配复杂的问题，论文提出基于小窗口策略的蚁群优化算法。采用链路可持续时间和波长空闲率作为启发函数，在实现负载均衡的同时，降低网络的拥塞率；引入小窗口策略引导蚂蚁在最小路由请求区域内进行选路，提高了算法的收敛速度；通过计算相邻链路空闲波长的交集，实现了由单只蚂蚁同时完成路由选择和波长分配。对单主星和双主星两种场景下的算法性能进行了仿真分析，结果表明：与经典的Dijkstra+FF算法相比较，单主星和双主星时的网络拥塞率最高分别降低了0.5和0.7，网络资源利用率改善最高可达到0.45和0.50。

分布式卫星光网络；波长路由分配；蚁群算法；小窗口策略；拥塞率

1 引言

气象、环境和军事领域应用的不断拓展，一方面使卫星传输的信息量呈现出爆炸式的增长，另一方面，对卫星的功能也提出了新的要求，如立体成像、精确定位等。这对于目前基于微波链路的卫星网络提出了挑战。而基于激光链路的分布式卫星系统由于能够提供雷达探测所需要的各种基线组合，具有抗摧毁性强，技术更新快，成本低等优势，同时兼具光通信高速率、宽带宽的特点，能够很好地满足未来各种空间业务的技术要求。

在分布式卫星光网络中，路由技术是决定整个网络性能的重要方面。其中，波长路由能够提供粗的交换粒度，对于具有大量遥感探测和视频信息的业务，能够避免频繁的复用和解复用过程，提高路由的效率。波长路由的核心问题是波长和路由的分配(RWA)问题，而动态的RWA问题已经被证明是NP-hard问题[4,5]。最初的解决办法是将RWA问题分解为路由选择和波长分配两个问题，即先选路，再根据一定的策略对路径进行波长分配。分图层模型[6]通过将物理拓扑映射成多个分层图的方法，将动态的RWA问题分解成一个3维模型；整数线性规划(ILP)方法[7,8]是通过求解多约束条件下目标函数的最大或最小化问题来处理RWA问题。尽管两种方法都能最终找到最优的解，但是算法耗时过长，对于大型网络是不可接受的。利用遗传算法解决动态RWA问题能够缩短选路的时间，但是算法的收敛性较差，存在容易陷入局部最优的问题。采用蚁群算法不仅可以实现负载均衡和多目标优化，而且可以使路由选择和波长分配同时完成，为解决动态RWA问题提供了一种新的思路。

然而，到目前为止，有关波长路由的研究大都是基于地面光纤网络的，对卫星光网络的波长路由问题研究却非常少。事实上，卫星光网络中的动态RWA问题是一个比地面光网络更加复杂的问题，因为它要同时考虑多个因素的限制，例如：星间距离处在不断变化中；卫星的持续运动造成不同链路的可持续时间是不一样的；卫星网络中对光通路的评价需要综合考虑跳数、路径可持续时间以及延时等多个因素。尤其是分布式卫星网络中卫星数目增多，信息交换更加频繁，进一步增加了RWA的复杂性。

基于此，本文提出了一种基于小窗口策略的蚁群优化算法，来解决分布式卫星网络中RWA的复杂性问题。算法通过将蚂蚁选路限制在最小路由请求区域内，降低了运算量，提高了路由搜索的收敛速度。

2 模型分析

2.1 转移概率函数

蚁群优化算法是模拟自然界中蚂蚁寻找路径行为得到的一种仿生算法。研究人员经过不断的追踪，发现蚂蚁群体总能在一定时间内找到从蚁穴到食物源的一条最短通路。这是因为蚂蚁在觅食的过程中会在所走过的路径上留下一些被称作“信息素”的挥发性化学物质。而这些“信息素”会被同一群体中后续的蚂蚁感知到，并影响后续蚂蚁的寻路行为。实验证明，蚂蚁选择信息素浓度高的路径的概率要比选择信息素浓度低的路径概率大。将网络中寻找路由的过程抽象成蚂蚁的觅食过程，转移概率函数用来衡量蚂蚁从一个节点向下一跳节点转移的概率大小。假设网络中每一条链路都有相同数目的可用波长，每一个节点都维持一张路由表用来存放可选节点的地址和相应的转移概率。当每一只蚂蚁到达一个节点时，首先要判断该节点是否为目的节点，如果不是，那么就将该节点放入禁忌表中并依据转移概率大小前往下一节点。以此重复，直到到达目的节点为止。

为了给出转移概率函数的表达式，首先对算法中涉及到的概念和主要参数进行说明。

(1)禁忌表Tabu()用来存储时刻蚂蚁已经到达过的所有节点。

(3)D()表示时刻节点和间的距离。

(4)波长空闲率I()表示时刻节点和间空闲波长数占总波长数的概率，由式(1)给出：

式中，为节点间的波长总数，n()为时刻节点和间被占用的波长数。

(5)TK()表示从时刻算起，链路L可持续的时间。在极轨星座中，由于卫星运行到极地地区时相对速度比较高，相邻轨道间卫星通信设备处于关闭状态，因此即将进入极地地区的轨间链路可持续时间将小于赤道附近轨间链路的可持续时间。

综合考虑星间距离、链路可持续时间和波长空闲率的限制，节点间的概率转移函数为

为了能够利用前面蚂蚁选路留下的信息，在每一代蚂蚁完成选路后需要对信息素进行更新。更新的原则为：被前面蚂蚁选到的链路，其信息素适当地增加，没有被前面蚂蚁选到的链路，其信息素适当地减少。假设为上一代蚂蚁选路时链路L上的信息素，则这一代蚂蚁选路时的信息素更新为

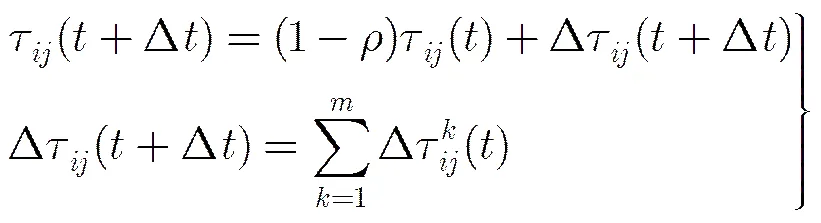
对于单只蚂蚁在链路L上产生的信息素的计算，采用基于全局信息的Ant-Cycle模型能够保证信息素和期望值的均衡发展，其表达式为

式中，为上一代蚂蚁完成选路留下的总的信息素，J为蚂蚁经过的路径长度。

2.2 波长和路由分配规则

为了实现路由选择和波长分配由一只蚂蚁同时完成，本文采用可用波长求交集的思想。当蚂蚁到达每一个节点时，首先查找以该节点为端点的各个链路的可用波长情况，然后决定前往哪一个节点。如果各条链路均没有可用波长，则宣告本次选路失败。具体过程如图1所示。蚂蚁从节点1出发，当到达节点2时，首先搜索拓扑情况并对照禁忌表确定可选的下一跳节点。然后分别计算12上可用波长(1,2)与23,24,25上可用波长(2,3),(2,4),(2,5)的交集。由于3个交集均不为空，因此节点3, 4, 5都可作为下一跳节点。假设依据状态转移概率选择了节点5，记录当前可用波长集合(1,2)∩(2,5)，并计算(1,2)∩(2,5)与(5,6),(5,7),(5,8) 的交集。此时发现，节点6和节点8仍然能够满足要求，而(5,7)与(1,2)∩(2,5)的交集为空，所以节点7不能作为下一跳节点。以此类推，在每一个节点上重复该过程，当蚂蚁到达目的节点时就可以同时完成路由的选择和波长的分配。

2.3 小窗口策略

为了后文表述清楚，先对星座和星群的概念加以区分。星座是指为了增加卫星对地面的覆盖区域或缩短重访时间，由多颗卫星稀疏分布组成的卫星空间结构，星座中各卫星之间无动力学联系，根据需要星间通信可有可无；星群是指为了实现一个大的“虚拟卫星”功能，由多颗卫星密集分布组成的卫星空间结构，星群中各卫星之间满足严格的动力学关系和约束条件，各星之间分布距离短，且需要通过频繁的星间通信和信息交换共同完成空间任务。本文提到的星群实际包含两个层面：首先是单个星群，即分布在很小空间范围内的、类似于一个大“虚拟卫星”的编队卫星；其次，是由多个星群组成的一个大的星座，每一个星群相当于星座中的一个卫星。

图1 波长分配示意图

为了实现分布式星群内部以及星群之间的通信，目前主要采用两级结构的网络拓扑，即每个星群内有一个“主星”，负责管理群内各颗卫星之间的通信并与其它星群的主星相互交换信息。然而，当数据量较大时，一颗主星既要与星群内部多颗卫星通信，又要负责星群间的通信，通信阻塞的概率和风险随之增大。基于此，研究人员又提出了“双主星”的结构，用于提高通信的灵活性和分担风险。图2给出了单主星和双主星两种结构下星群间通信的虚拟拓扑。单主星结构时受天线数目限制，每个星群只能与前后左右4个星群建立链路，如图2(a)所示；采用双主星结构时，由于可用的天线数目翻倍，并且两颗主星可以分别控制所属天线的姿态，每个星群可以与周围8个星群建立链路，如图2(b)所示。

图2 网络虚拟拓扑

蚁群算法在解决RWA问题时蚂蚁的选路是基于全网所有的可达节点，而随着节点数目的增加，算法的运算量将按指数形式增长。当网络规模比较大，或者采用双主星结构时，大的运算量将使算法的收敛速度降低，影响路由的时效性。为了降低运算量，提高算法的收敛速度，本文借鉴辅助定位按需路由(LAOR)算法中限定请求区域的方法，将路由选择的开销保持在最低限度。该方法的理论基础是，对于给定的源和目的卫星节点，基于传输延时的最短路径通常位于由该目的和源节点确定的最小矩形区域内，称为最小路由请求区域(MRRR)。根据源节点和目的节点的位置，MRRR的确定可以分为两种情况，如图3所示。图中为一个轨道内卫星的个数。如果源/目的节点的坐标满足不等式，则MRRR如图3(a)所示；如果满足，则MRRR如图3(b)所示。

图3 小窗口策略示意图

MRRR限制了路由搜索的范围，为了保证算法实现过程中每只蚂蚁的选路都能在MRRR规定范围内的节点进行，需要对转移概率函数进行适当地修改，如式(5)所示：

式中，M表示由源/目的节点(,)确定的MRRR内的节点集合。MRRR就像为每一只蚂蚁安装的窗户一样，只有落在窗口内的节点才能被选择为下一跳节点，因此我们称这种算法为基于小窗口策略(Small Window Strategy, SWS)的蚁群算法。

值得一提的是，基于蚁群算法的波长路由技术在每个节点的选路策略均是基于全网信息进行的；在这种场景中，如果不加任何限制，对于分布式卫星网络节点数目多、信息交换频繁的情况，由全网信息更新产生的额外开销将是非常巨大的。针对这一问题，我们在网络信息更新时也采用了类似于小窗口策略的思想，对网络信息交换的范围进行了一定的限制，具体方法为：当网络中任意两个节点需要进行通信时，以该源/目的节点连线为对角线画矩形区域，在本次链路建立过程中，当前节点选路所需要的“全网信息”都只限定在该矩形区域内；并且只有当路径请求产生时才进行“全网信息”的更新，无请求则不更新。基于该思想获得的更新信息不仅能满足文中蚁群算法的应用需求，而且大大降低了传统全网信息交换造成的巨大额外开销。

根据以上分析，基于SWS的蚁群算法伪代码如表1所示，终止条件为达到迭代次数。

表1小窗口策略(SWS)的蚁群算法伪代码

3 仿真分析

本文以极轨星座的分布式卫星网络为例对基于小窗口策略的蚁群算法性能进行仿真，包括单主星和双主星两种结构，虚拟拓扑如图2中所示。仿真中，假设星群内部信息交互畅通，因此将每一个分布式星群抽象为一个卫星节点，对于双主星结构按照图2(b)中8条星间链路的方式处理。星座包含6个轨道面，每个轨道面内12个节点。反向缝两侧的卫星无法建立星间链路，当卫星运行至南北纬时轨间链路关闭。对于星间距离，建立星间距离邻接矩阵，将每颗卫星周围能与之建立链路的卫星星间距离按照大小比例设置为有限常数，距离较远而无法通信的卫星星间距离设为无穷大。对于链路可持续时间，建立链路可持续时间的邻接矩阵，同一轨道内前后两颗卫星链路可持续时间为1；按照大小比例，不同轨道间两个卫星越向着极地运动，链路可持续时间越小。对于波长空闲率，每只蚂蚁在当前节点根据下一跳可到达节点及通往该节点的波长使用情况，计算每一个可用波长的空闲率。所有节点没有波长转换能力和排队等待机制，因此光通路必须遵循波长连续性限制，并且路由请求一旦被拒绝，将立即被抛弃。仿真中设定迭代次数为100次，每次迭代共有30只蚂蚁。由于仿真中源和目的节点是随机产生的，所有的结果将通过统计平均得出。

图4给出了单主星和双主星情况下网络的拥塞率性能，Dijkstra+FF算法用于对比参照。仿真中，每颗卫星与相邻卫星之间有4个可用波长。可以看出，在很大的业务强度范围内蚁群算法的拥塞率要明显低于Dijkstra+FF算法，单主星时，拥塞率改善最高可以达到50%，而双星是可高达70%。与单主星的情况相比，双主星的网络拥塞率在低业务强度时只是略有改善，但当业务强度比较大时拥塞率改善十分显著。这是因为当业务强度比较低时，无论是单主星还是双主星，网络可用资源都比较多，出现拥塞的概率也比较小；但是当业务强度比较大时，双主星的可用网络资源要明显多于单主星，因此拥塞率也明显要低。

图5为3种场景下网络资源利用率的对比情况。从图中可以看出，单主星和双主星情况下，蚁群算法的资源利用率都要明显高于Dijkstra+FF算法，在不同的业务强度下最大可分别高出0.45和0.50。同时，单主星时利用率随着业务强度的增加单调下降，而双主星时利用率先增大，随后开始减小。这是因为随着业务强度的增加，越来越多的波长信道不断被占用，单主星时由于可用的网络资源相对较少，因此距离较远的源/目的节点由于受波长连续性限制难以找到光通路，因此对网络资源的利用率逐渐减小；双主星时，由于增加了与倾斜方向4颗卫星之间的链路，相同业务强度条件下网络资源要明显多于单主星，业务强度开始增加时并不影响源/目的节点的找路，但当业务强度增加到一定程度时网络资源出现短缺，因此出现了类似于单主星时利用率下降的情况。

图6给出了单主星和双主星情况时不同波长数目条件下网络的拥塞率对比，图中所标注的波长数均指单颗卫星之间的可用波长数。从图中可以看出，两种情况下，增加波长数均能降低网络的拥塞率；对于单主星的情况，业务强度在130 Erl以下，拥塞率保持缓慢增长，超过130 Erl后增长较快；双主星时由于增加了可用的链路数，业务强度在210 Erl时拥塞率仍然保持缓慢增长，并且在100 Erl以下出现了“0”拥塞的情况。

图7对比了基于小窗口策略和无小窗口策略的蚁群算法在单主星和双主星网络中应用时的收敛特性。为了充分观察算法的性能，仿真中选取距离较远的(7,1)和(2,6)两个节点分别作为源节点和目的节点(如图2中所示)，网络业务强度设置为170 Erl。从图中可以看到，对于单主星的情况，无小窗口策略时算法在第55次迭代时收敛于最佳路径，而带小窗口策略时在第25次迭代时就开始收敛，减少了30次迭代；对于双主星的情况，无小窗口策略时算法收敛于75次迭代，而小窗口策略时收敛于48次迭代，减少了27次迭代。另外，与单主星情况相比，双主星由于增加了倾斜方向上的4条链路，最佳路径的跳数变为7跳，比单主星减少了3跳；然而，也正是由于可选的链路数增加，无小窗口和有小窗口策略时其收敛的时间也分别推迟了20和23次迭代。

图8以单主星情况为例，对基于小窗口策略和无小窗口策略的蚁群算法性能做了进一步的对比。图8(a)给出了两种情况下最佳路径跳数的对比，其中横坐标为整个网络的平均波长利用率，纵坐标为通过计算100对源/目的节点得到的最佳路径跳数的平均值。从图中可以看出，小窗口策略得到的最佳路径跳数要少于无小窗口的情况。图8(b)为两种情况下的拥塞率对比。可以看出，随着网络平均波长利用率从0.1增加到0.8，无小窗口时的拥塞率始终略低于小窗口策略时。这是因为MRRR限制了路由选择的区域，将一部分可选的节点排除在外。也就是说，小窗口策略是通过牺牲一定的拥塞率来降低蚁群算法的运算量，提高路由搜索的收敛速度。

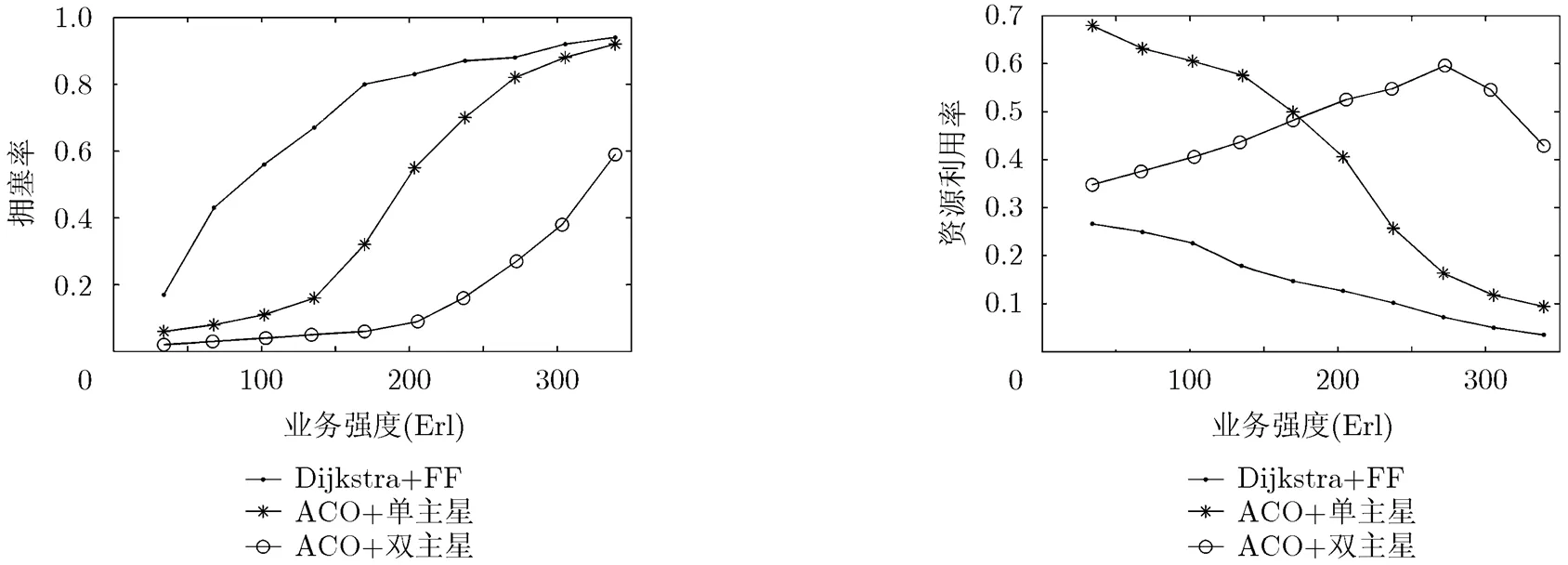
图4 拥塞率对比图5 资源利用率对比

图6 不同波长数目时拥塞率对比

图7 收敛性能对比

图8 最佳路径跳数和拥塞率对比

4 结论

为了解决分布式卫星光网络波长路由分配复杂的问题，本文设计了一种基于小窗口策略的蚁群优化算法，并对算法在单主星和双主星网络结构中的性能进行了仿真分析。与经典的Dijkstra+FF算法相比，单主星和双主星时的网络拥塞率最高分别降低了0.5和0.7，网络资源利用率改善最高可达到0.45和0.50。尽管引入小窗口策略后一定程度地牺牲了网络拥塞率，但是无论是单主星还是双主星结构，算法的收敛速度都显著提高，这对于网络规模大、节点数目多的分布式卫星网络具有很好的现实应用价值。

[1] Dang Zhao-hui and Zhang Yu-lin. Optimization of communication network topology for navigation sharing among distributed satellites[J]., 2013, 51(1): 143-152.

[2] 李世强, 禹卫东. 分布式卫星SAR相位同步的实现方案及试验验证[J]. 电子与信息学报, 2012, 34(2): 356-360.

Li Shi-qiang and Yu Wei-dong. Implementation and verification for phase synchronization of distributed satellite SAR[J].&, 2012, 34(2): 356-360.

[3] Sandau R. Status and trends of small satellite missions for Earth observation[J]., 2010, 66(1/2): 1-12.

[4] 程希, 沈建华. 一种基于改进蚁群算法的光网络波长路由分配算法[J]. 电子与信息学报, 2012, 34(3): 710-715.

Cheng Xi and Shen Jian-hua. An improved ant colony algorithm for routing and wavelength assignment in optical networks[J].&, 2012, 34(3): 710-715.

[5] Karasan E and Ayanoglu E. Performance of WDM transport networks[J]., 1998, 16(7): 1081-1096.

[6] Xu Shi-zhong, Li Le-min, and Wang Sheng. Dynamic routing and assignment of wavelength algorithms in multifiber wavelength division multiplexing network[J]., 2000, 18(10): 2130-2137.

[7] Yetginer E, Liu Ze-yu, and Rouskas G N. Fast exact ILP decompositions for ring RWA[J]., 2011, 3(7): 557-586.

[8] Krishnaswamy R M and Sivarajan K N. Algorithms for routing and wavelength assignment based on solutions of LP- relaxations[J]., 2001, 5(10): 435-437.

[9] Zang S, Martel C, and Mukherjee B. Dynamic traffic grooming in elastic optical networks[J].,, 2013, 31(1): 4-12.

[10] Qin H, Zhang S, and Liu Z. Dynamic routing and wavelength assignment for limited-rang wavelength conversion[J]., 2003, 7(3): 136-138.

[11] Shen G, Bose S K, Cheng T H,.. Effcient heuristic algorithms for light-path routing and wavelength assignment in WDM networks under dynamically varying loads[J]., 2001, 24(3): 364-373.

[12] Ming Tsung-chen, Lin B M T, and Tseng Shian-shyong. Ant colony optimization for dynamic routing and wavelength assignment in WDM networks with sparse wavelength conversion[J]., 2011, 24(2): 295-305.

[13] Triay J and Cervelló-Pastor C. An ant-based algorithm for distributed routing and wavelength assignment in dynamic optical network[J]., 2010, 28(4): 542-552.

[14] 郑滟雷, 顾畹仪, 连伟华, 等. 采用蚁群算法解决光网络中动态及分布式RWA问题的方法[J]. 北京理工大学学报, 2009, 29(12): 1104-1109.

Zheng Yan-lei, Gu Wan-yi, Lian Wei-hua,.. Ant colony algorithm-distributed strategy for solving RWA problem in optical WDM network[J]., 2009, 29(12): 1104-1109.

Research on Routing and Wavelength Assignment Based on Ant Colony Optimization in Distributed Satellite Optical Network

Dong Yi Zhao Shang-hong Li Yong-jun Zhao Jing Deng Bo-yu

(,,’710077,)

To solve the complexity of Routing and Wavelength Assignment (RWA) in distributed satellite optical network, the Ant Colony Optimization (ACO) based on Small Window Strategy (SWS) is put forward. The link duration and the wavelength idle ratio are used as the heuristic functions for load balancing and decreasing the blocking probability. The small window strategy is introduced to limit the routing in the Minimum Routing Request Range (MRRR) and promote the convergence speed. By calculating the intersection of idle wavelengths on the adjacent links, the algorithm can accomplish the routing selection and wavelength assignment by a single ant. The properties of the algorithm in both single and double master satellites cases are analyzed, and the results show that compared with Dijkstra+FF algorithm, the blocking probability of ACO can reduce at most 0.5 and 0.7 for single and double master satellites respectively, and the improvement of resource utilization ratio can reach to 0.45 and 0.50.

Distributed satellite optical network; Routing and Wavelength Aassignment (RWA); Ant Colony Optimization (ACO); Small Window Strategy (SWS); Blocking probability

TN915.63

1009-5896(2015)11-2650-07

10.11999/JEIT150252

2015-02-22；改回日期：2015-07-03；

2015-08-24

董毅 dongyi_19870129@sina.com

国家自然科学基金(61231012)

The National Natural Science Foundation of China (61231012)

董毅：男，1987年生，博士生，研究方向为激光空间信息技术.

赵尚弘：男，1964年生，教授，博士生导师，研究方向为激光与光通信技术.

李永军：男，1979年生，副教授，硕士生导师，研究方向为光通信技术.

赵静：女，1988年生，博士生，研究方向为激光空间信息技术.