一种单接收天线下的空时分组码识别方法

张立民 闫文君 凌 青 孔东明



一种单接收天线下的空时分组码识别方法

张立民①闫文君*②凌 青②孔东明③

①(海军航空工程学院融合所 烟台 264001)②(海军航空工程学院电子信息工程系 烟台 264001)③(海军装备部 太原 030027)

该文针对全盲条件下单接收天线的空时分组码(STBC)识别问题，提出一种基于四阶累积量识别方法。使用接收信号的四阶累积量作为特征参数，利用高阶累积量对零均值高斯噪声不敏感的特性，首先求取各种STBC的四阶累积量理论值，再对采样信号四阶累积量进行区间检测，从而实现STBC的识别。该算法不需要信道信息和噪声参数，仿真结果表明，该算法在单天线条件下性能较好。

多输入多输出；单天线识别；高阶累积量；空时分组码

1 引言

MIMO系统以其充分利用空间资源的优势，成为下一代无线通信系统中的关键技术。空时分组码(Space-Time Block Code, STBC)作为一种基于MIMO系统的编码方案，其盲识别问题受到越来越多的关注。近年来，对STBC的盲识别问题的研究主要有两种：一是基于最大似然的方法[1,2]，二是基于特征提取的方法。基于最大似然的方法[1,2]通过计算接收信号的最大似然方程来进行识别，该方法需要预先估计信道的信息和时频信息等，而且算法的计算复杂度非常高。基于特征提取的方法利用信号的不同特征进行识别，其中基于二阶统计量的算法分别通过设定门限区分不同二阶统计特征[3]，计算相关矩阵估计值与实际值之间最小距离[4]，计算相关矩阵的诱导峰值[5]和衡量互相关矩阵[6]的方法进行识别，然而基于二阶统计的算法在全盲条件下，仅对部分码率较小的STBC识别效果较好。基于循环统计量的方法和基于高阶累积量的方法[11]分别通过检测样本的循环统计量和高阶累积量来进行区分。除此之外，文献[12]提出通过Kolmogorov-Smirnov(K-S)检测的方法识别STBC的方法。上述许多算法仅对SM(Spatial Multiplexing )和Alamouti STBC进行了识别，没有分析其他常用STBC的性能；且上述算法均在多天线条件下进行讨论，甚至有算法要求接收天线数量大于发射天线数量[1,3,4]。然而，在实际应用中，接收端天线数目的增加会影响接收端接收功率、成本等，越少的接收天线越有利于节约资源和成本，单接收天线条件下的STBC盲识别是现阶段研究的重点之一[13]。现阶段研究中，仅有一篇文献[13]对单天线条件下的空时分组码盲识别问题进行了针对性研究，该文献采用基于离散傅里叶变换的方法对常见的4种空时分组码进行识别，该算法达到了识别不同空时分组码的目的，但在低信噪比下，算法识别性能较差。

本文提出一种全新的单接收天线条件下基于特征提取的STBC识别方法。该方法通过计算接收信号的四阶累积量并对其进行区间检测，以达到识别不同STBC的目的。该方法不需要预先估计信道信息和噪声信息，在低信噪比下区分性较好。

本文章节安排如下：第2节介绍本文用到的信号模型、假设条件和STBC类型；第3节描述高阶累积量的定义、接收信号四阶累积量理论值推导和区间检测识别方法及其阈值的确定；第4节针对不同采样数和不同信道参数的条件进行仿真，同时与现有STBC识别算法进行对比，得出结论。

2 信号模型和STBC选取

2.1信号模型

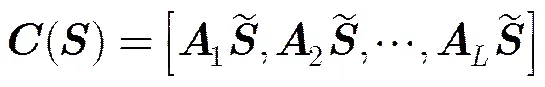
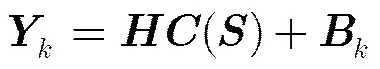
2.2假设条件

本文的识别算法在以下假设条件下进行：

假设1 接收信号经过频率平坦Nakagami-衰落信道，，则有,和，其中[14]，表示取均值。

假设3 假设传输信号独立同分布[1]，且经过正交相移键控(QPSK)调制，其平均信号能量，则有以及[16]。

2.3 STBC选取

不失一般性，本文对多路复用(Special Multiplexing, SM)和3种最常见的线性STBC进行区分，分别为：

(1)发射信号为SM[3]，发射天线数：

(2)发射信号为Alamouti STBC，简称为AlSTBC[17]，发射天线数，码矩阵长度，码率为1：

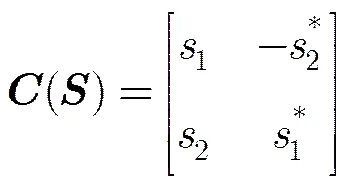
(3)发射信号为OSTBC3[3]，发射天线数，码矩阵长度，码率为，其码矩阵形式为

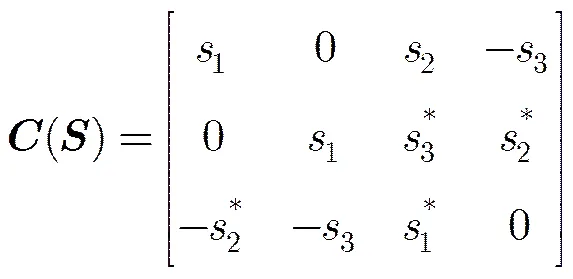
(4)信号为OSTBC4[3]，发射天线数，码矩阵长度，码率为，其码矩阵形式为

3 算法分析

3.1高阶累积量模型

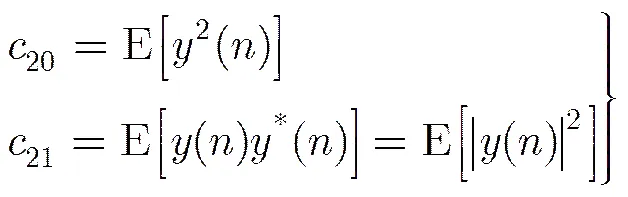
其零时延四阶累积量可表示为3种形式：

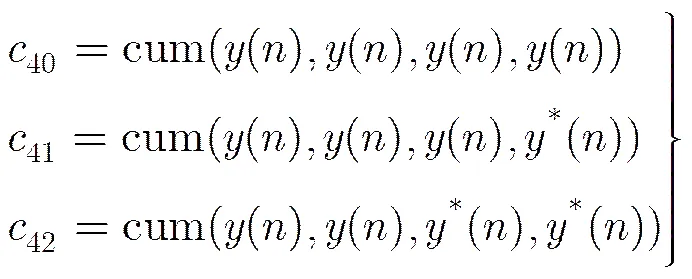
式(3)和式(4)表示的是零时延条件下的累积量。对于零均值，四阶累积量可表示为[18]

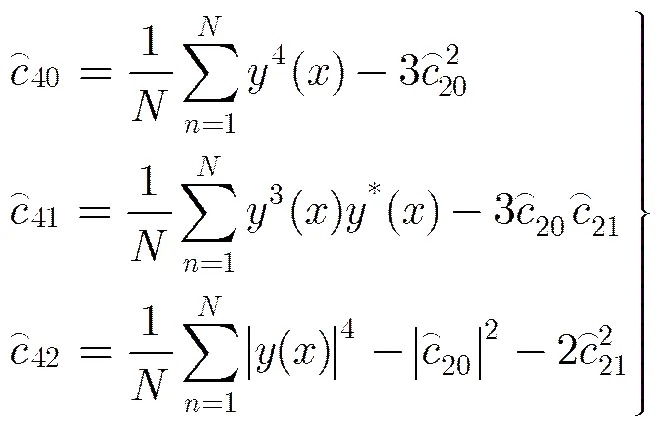
特别地，零均值高斯信号的高阶累积量(阶数大于2)等于零[19]，零均值高斯噪声的高阶累积量，信号的高阶统计分析和处理本质上就是对非高斯部分的分析和处理，观测接收信号的四阶累积量时，可以忽略噪声对于观测值的影响[19]。接收信号四阶累积量可表示为

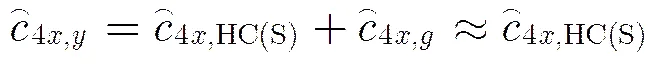
3.2 接收信号的四阶累积量

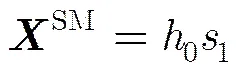
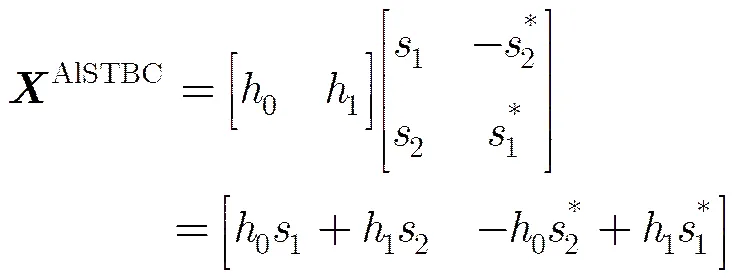
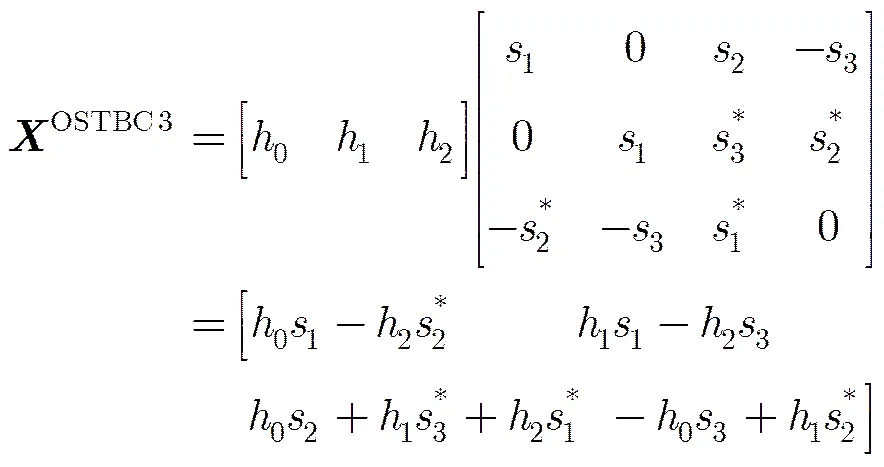
各接收信号的四阶累积量为

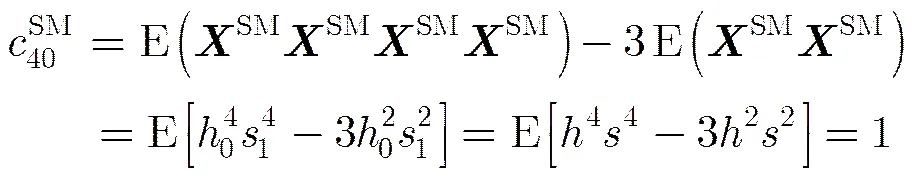
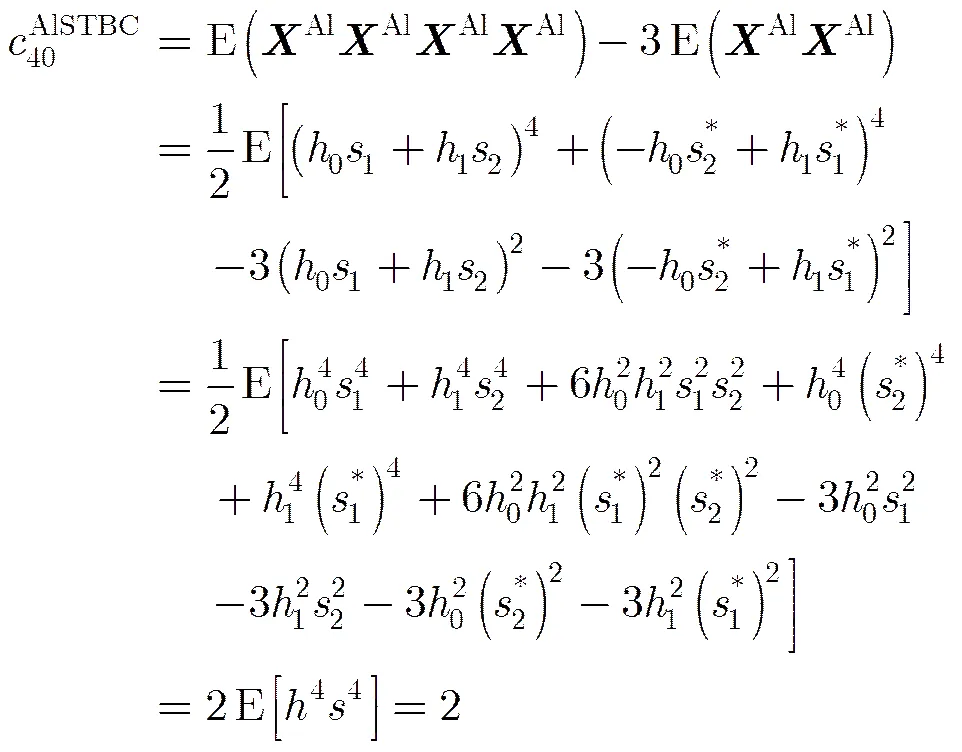
OSTBC3和OSTBC4的推导过程较长，在此不做详细推导。与AlSTBC推导过程类似，OSTBC3的四阶累积量和OSTBC4的四阶累积量分别为

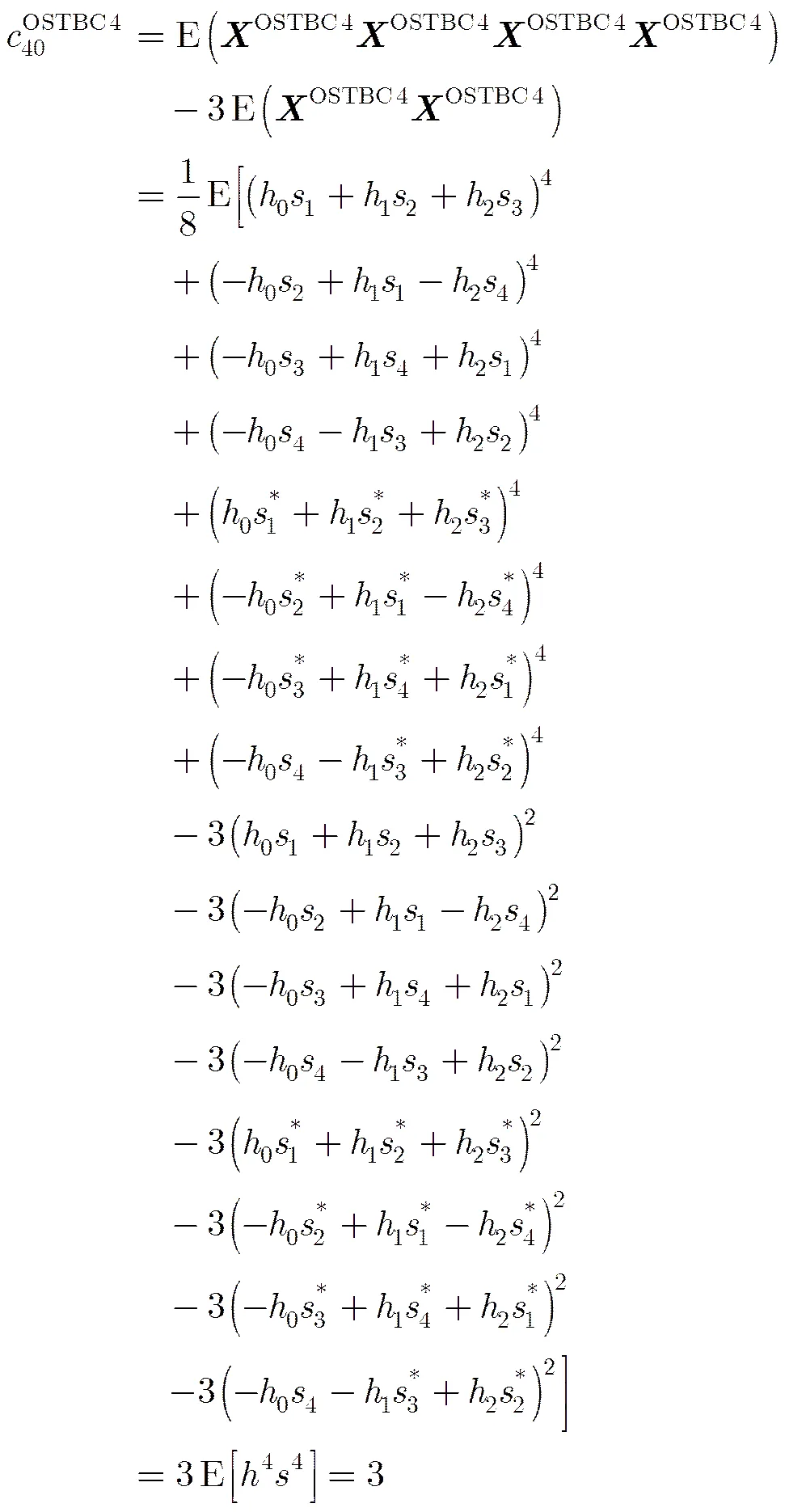
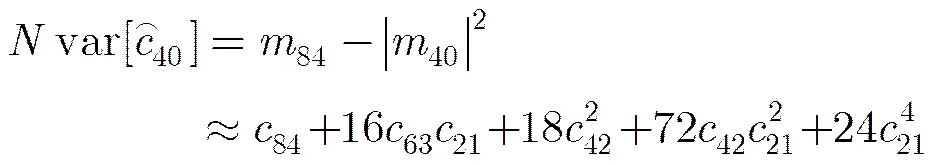
3.3判决方法和判决门限取值

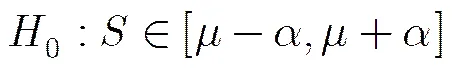
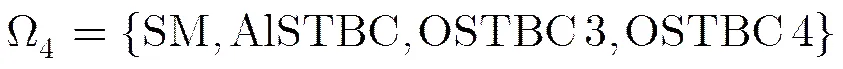
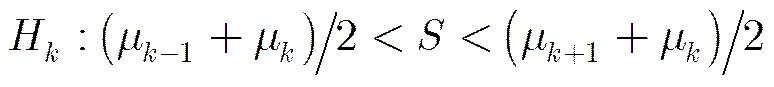
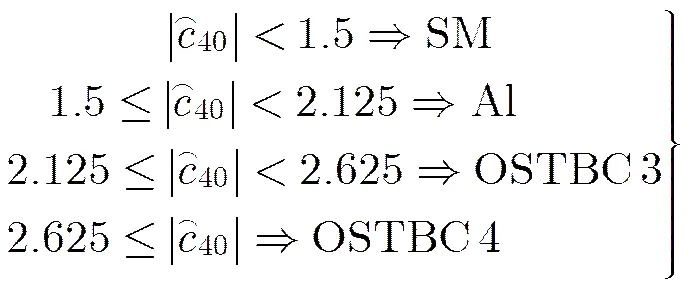
定义总体识别概率[16]：

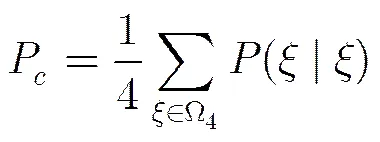
表1不同STBC的理论值以及在不同信噪比下样本方差估计值(采样数)

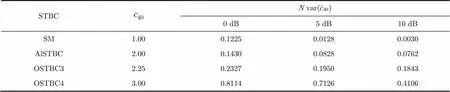
STBC 0 dB5 dB10 dB SM1.000.12250.01280.0030 AlSTBC2.000.14300.08280.0762 OSTBC32.250.23270.19500.1843 OSTBC43.000.81140.71260.4106

4 仿真和结果

本节通过计算机仿真对算法有效性进行验证。仿真中无特殊说明，噪声均为高斯白噪声，调制方式为QPSK调制。仿真使用蒙特卡洛仿真，蒙特卡洛次数均为1000次。

仿真1 接收信号四阶累积量均值变化分析

仿真过程：为准确观察样本四阶累积量的变化，在该仿真中，取较大数量的样本进行观测，以便与表1中理论值作比较，令采样数量。仿真中Nakagami-衰落信道。如图1所示，纵坐标表示4种空时分组码的四阶累积量的绝对值。在样本足够大()的条件下，4种空时分组码样本的四阶累积量值绝对值分别趋于4个稳态值：，这与推导的理论值相同，说明该算法具有一定的可行性。

仿真2 识别概率与采样数关系分析

仿真过程：图2为不同信噪比下，采样数不同识别概率的分布情况，其中仿真的信道为Nakagami-衰落信道，。样本采样数分别为2048, 4096和8192。随着采样数的增加，识别概率也相应增加。说明大量的采样样本有利于发挥高阶累积量的优势，不仅抑制了噪声特性，同时提高了高阶累积量作为特征参数的性能。由图2可以看出，算法在样本采样数时，算法识别概率可达到0.98，因此，样本选取时，样本数应取，以保证识别概率近似为1。

仿真3 识别概率与Nakagami-信道参数的关系

仿真4 识别概率与调制方式的关系

2.2节中假设条件3，假设符号是经过QPSK调制的，本节讨论本文识别方法在其他线性调制方式下的适应性。考虑4种调制方式QPSK, 8PSK, 16QAM和64QAM，本文不考虑BPSK是由于BPSK调制的是实数信号，而本文研究的是复信号，实际上，BPSK调制方式同样适用于本文算法。4种调制方式下符号的统计特性如表2所示。

在4种调制方式下，输入信号的统计特性不同，这就要求在识别前预先估计信号的调制方式[5,21]。QPSK调制方式下识别不再赘述。当调制方式为8PSK时，4种空时分组码的四阶累积量均为0，说明本文算法不适用于8PSK调制，实际上当调制方式为PSK()时，本文算法就不再适用；当调制方式为MQPM时，4种空时分组码的四阶累积量可明显区分。图4为不同调制方式下识别效果。仿真过程中样本采样数，信道为Nakagami-信道，。可以看出16QAM和64QAM识别概率相差不大，3种调制方式下识别概率均能达到0.94以上，识别效果较好。

仿真5 本文方法与其他算法性能比较

(1)基于最大似然识别的算法[1]需要预先求取信道参数、噪声功率和调制方式，识别效果依赖于对这些参数估计的结果。本文算法则不需要对这些参数进行估计，更适用于实际系统。

(2)本文算法的识别概率远好于基于二阶相关矩阵的算法[3]，即便在高信噪比下，后者的识别概率也不大于0.5，二阶相关矩阵的算法在单天线下只对SM和OSTBC4区分性较好，AlSTBC和OSTBC3的识别概率为零，导致总体识别概率较低[3]。

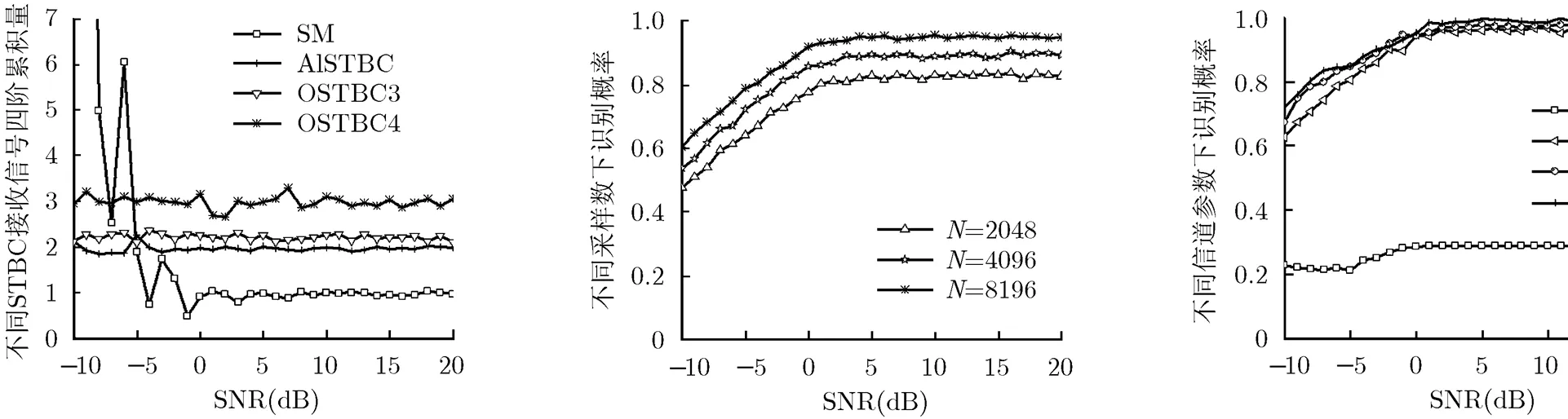
图1 4种空时分组码接收信号四阶累积量随信噪比变化  图2 不同采样数下正确识别概率   图3 不同信道参数下正确识别概率

表2不同调制方式下统计特性

QPSK0-11.002.002.253.00 8PSK000000 16QAM0.1-0.650.651.301.461.95 64QAM0-0.620.621.241.391.85

图4 不同调制方式下正确识别概率          图5 不同识别算法性能比较

(3)与基于离散傅里叶变换的算法[13]相比，本文算法在高信噪比下()性能较差，但本文算法在低信噪比下的识别性能明显优于前者。

(4)由图1, AlSTBC和OSTBC3理论值较为接近，在接收样本小和低信噪比的情况下较难区分。若这两种码其中一种在接收端排除，则可大幅提高总体识别概率。

5 结束语

针对单天线条件下，STBC盲识别问题，本文提出了采用基于高阶累积量的解决方案。该算法利用不同STBC表现出不同高阶累积量这一性质，将不同STBC接收信号的高阶累积量进行区间检测，在不需要信道信息和噪声信息的条件下进行STBC识别。识别结果表明，该算法在低信噪比条件下性能远好于现有针对单天线STBC识别的算法。算法性能受信道参数和样本数量影响，随着Nakagami-信道参数和样本数量的增大，算法识别概率有提高。

[1] Choqueuse V, Marazin M, Collin L,.. Blind recognition of linear space time block codes: a likelihood-based approach [J]., 2010, 58(3): 1290-1299.

[2] Marey M, Dobre O A, and Liao B. Classification of STBC system over frequency-selective channels[J]., 2015, 64(5): 2159-2164.

[3] Choqueuse V, Yao K, and Collin L. Hierarchical space-time block code recognition using correlation matrices[J]., 2008, 7(9): 3526-3534.

[4] Choqueuse V, Yao K, Collin L,. Blind recognition of linear space time block codes[C]. Proceedings of IEEE International Conference Acoustics, Speech and Signal Processing, Las Vegas, USA, 2008: 2833-2836.

[5] Marey M and Dobre O A. Blind modulation classification algorithm for single and multiple-antenna systems over frequency-selective channels[J]., 2014, 21(9): 1098-1102.

[6] Eldemerdash Y A, Dobre O A, and Liao B J. Blind identification of SM and Alamouti STBC-OFDM signals[J]., 2015 14(2): 972-982.

[7] Shi M, Bar-Ness Y, and Su W. STC and BLAST MIMO modulation recognition[C]. IEEE Global Telecommunications Conference,Washington, D.C., USA, 2007: 3034-3039.

[8] Marey M, Dobre O A, and Inkol R. Classification of space time block codes based on second-order cyclostationarity with transmission impairments[J]., 2012, 11(7): 2574-2584.

[9] DeYoung M, Health R, and Evans B L. Using higher order cyclostationarity to identify space-time block codes [C]. IEEE Global Telecommunications Conference, New Orleans, USA, 2008: 3370-3374.

[10] Karami E and Dobre O A. Identification of SM-OFDM and AL-OFDM signals based on their second-order cyclostationarity[J]., 2015, 64(3): 942-953.

[11] 赵知劲, 谢少萍, 王海泉. OSTBC信号累积量特征分析[J]. 电路与系统学报, 2013, 18(1): 150-155.

Zhao Z, Xie S, and Wang H. The characteristic analysis of cumulants of the OSTBC signals[J]., 2013, 18(1): 150-155.

[12] Mohammadkarimi M and Dobre O A. Blind identification of Spatial Multiplexing and Alamouti space-time block code via Kolmogorov-Smirnov(K-S) test[J]., 2014, 18(10): 1711-1714.

[13] Eldemerdash Y A, Dobre O A, Marey M,. An efficient algorithm for space-time block code classification[C]. IEEE Global Communications Conference, Atlanta, USA, 2013: 3329-3334.

[14] Beaulieu N C and Cheng C. Efficient Nakagami-fading channel simulation[J]., 2005, 54(2): 413-424.

[15] Swami A and Sadler B M. Hierarchical digital modulation classification using cumulants[J]., 2000, 48(3): 416-429.

[16] Eldemerdash Y A, Marey M, Dobre O A,. Fourth-order statistics for blind classification of Spatial Multiplexing and Alamouti space-time block code signals[J]., 2013, 61(6): 2420-2431.

[17] Alamouti S M. A simple transmit diversity technique for wireless communication[J]., 1998, 16(8): 1451-1458.

[18] 付卫红, 杨小牛, 刘乃安. 基于四阶累积量的稳健的通信信号盲分离算法[J]. 电子与信息学报, 2008, 30(8): 1853-1856.

Fu W, Yang X, and Liu N. Robust algorithm for communication signal blind separation fourth-order- cumulant-based[J].&, 2008, 30(8): 1853-1856.

[19] 张贤达. 信号分析与处理[M]. 北京: 清华大学出版社, 2011: 312-317.

Zhang X. Signal Analysis and Processing[M]. Beijing: Tsinghua University Press, 2011: 312-317.

[20] Srinath M D, Rajasekaran P K, and Viswanathan R. Introduction to Statistical Signal Processing with Application[M]. Englewood Cliffs, NJ: Prentice-Hall, 1996: 192-196.

[21] 钱国兵, 李立萍, 郭亨艺. 多入单出正交空时分组码系统的调制识别[J]. 电子与信息学报, 2015, 37(4): 863-867.

Qian G, Li L, and Guo H. Modulation identification for orthogonal space-time block code in multiple input single output systems[J].&2015, 37(4): 863-867.

A Method for Blind Recognition of Space-time Block Coding Using Single Receive Antenna

Zhang Li-min①Yan Wen-jun②Ling Qing②Kong Dong-ming③

①(,,264001,)②(,264001,)③(,030027,)

A novel and efficient algorithm is proposed for Space-Time Block Code (STBC) classification, when a single antenna is employed at the receiver. The algorithm exploits the discriminating features provided by the forth-order cumulants of the received signals. Higher-order cumulants (of order greater than 2) are used to eliminate the impact of noise.Firstly, the theoretical value of the different STBCs is caculated, then the samples of STBCs are classified with an interval detector. It does not require estimation of the channel information and signal-to-noise ratio of the transmitted signal. Simulation results show that the proposed method for blind recognition of STBC achieves good performance.

MIMO; Single antenna classification; Higher-order cumulants; Space-Time Block Code (STBC)

TN911.7

A

1009-5896(2015)11-2621-07

10.11999/JEIT150390

2015-04-02；改回日期：2015-07-08；

2015-08-27

闫文君 wj_yan@foxmail.com

国家自然科学基金(61102167)

The National Natural Science Foundation of China (61102167)

张立民： 男，1966年生，教授，研究方向为武器系统仿真、卫星信号处理.

闫文君： 男，1986年生，博士生，研究方向为MIMO技术、空时分组码识别.

凌 青： 女，1987年生，博士生，研究方向为MIMO技术、空时分组码识别.