基于算子和局部正交约束的信号自适应分解方法

衣晓蕾 彭思龙 栾世超



基于算子和局部正交约束的信号自适应分解方法

衣晓蕾*①彭思龙①栾世超②

①(中国科学院自动化研究所 北京 100190)②(中国航空综合技术研究所 北京 100028)

该文利用局部正交约束，采用反向投影策略，提出一种基于算子的信号自适应分解方法。该方法将输入信号建模为多个基本信号和一个残差信号之和，并且基本信号落在所定义算子的零空间中。通过仿真和实际信号的实验，展示了所提算法对于解决信号处理中的模式混叠问题的可行性，有效性和实用性。

自适应信号分解；局部正交；反向投影策略；零空间追踪

1 引言

零空间追踪算法[5,6]是一种基于算子的自适应信号分解算法。它将输入信号分解为子成分和,和相互正交且在该算法定义的参数化算子的零空间中。算子的下标表示该算子能够从信号中自适应地估计出来。然后，通过最小化式(1)实现从信号中得到子成分的估计值：

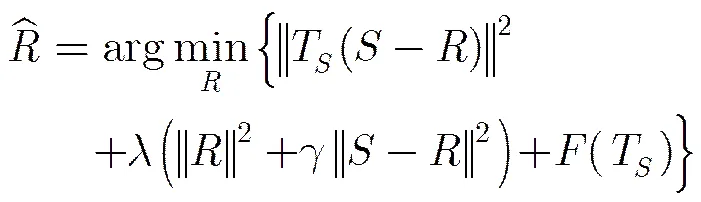
模式混叠问题是信号分解中经常发生的现象。按照文献[15]中的定义，模式混叠问题指出现了如下两种情况：(1)一个子成分中含有剧烈的尺度变换；(2)一个具有相似尺度的信号出现在不同的子成分中。文献[16]使用一个单频正弦信号作为掩膜信号来解决诸如这类信号分解中的模式混叠现象。由于采用的掩膜信号不是调频信号，所以该方法对于调频信号的分解并不有效。文献[15]提出对原信号加入大量高斯白噪声作为掩膜信号的EEMD算法，虽然给出一些实际信号的例子，但是对于相关理论分析不多，而且EEMD算法对于加入白噪声的方差和集成的数量非常敏感。

2 基于算子和局部正交约束的信号自适应分解方法

前面简要回顾了零空间追踪算法和信号分解中的模式混叠问题。下面，首先给出局部正交的定义和反向投影策略，然后提出基于算子和局部正交约束的信号自适应分解算法。

2.1 局部正交

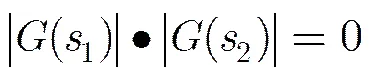
2.2 反向投影策略

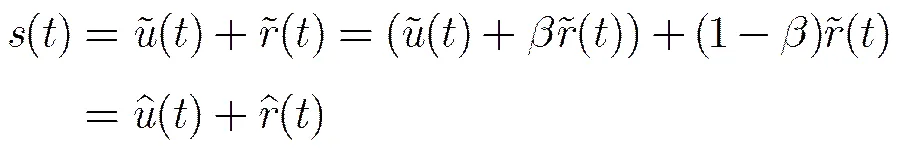
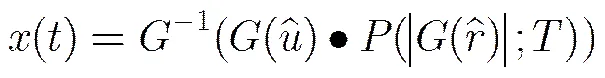
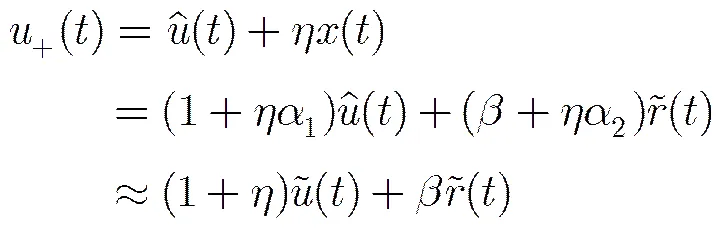
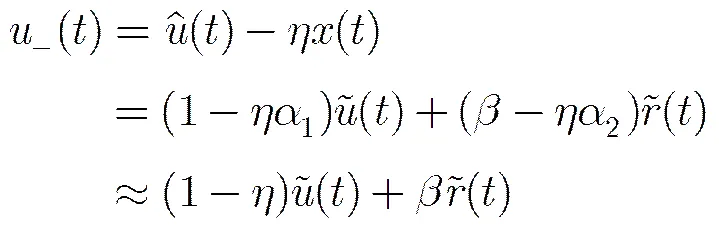
2.3 基于算子和局部正交约束的信号自适应分解方法

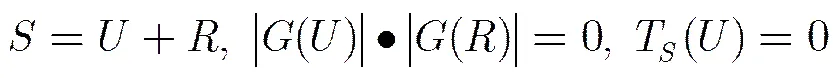
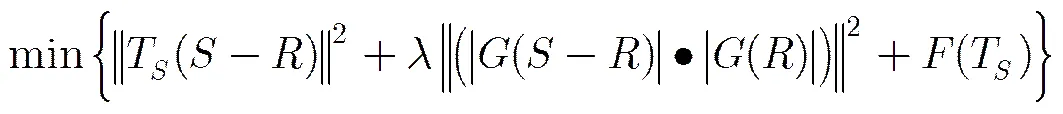
为了实现满足式(8)的信号模型的分解，本文利用局部正交约束，采用反向投影策略，提出表1的算法来求解优化问题式(9)。

表1基于算子和局部正交约束的信号自适应分解算法

步骤1 设输入信号为，给定停止条件；步骤2 对信号进行零空间追踪算法[3]分解，得到子成分和；步骤3 根据式(4)将子成分反向投影到，得到信号；步骤4 若信号满足，转向步骤8；否则继续步骤5；步骤5 对信号进行零空间追踪算法分解；得到；步骤6 对信号进行零空间追踪算法分解；得到；步骤7 更新提取的子成分：；转向步骤3；步骤8 输出希望提取的子成分：。

3 实验结果与分析

这一节采用不同的算法分别对一组仿真信号和实际真实信号进行分解，并将分解结果进行分析和比较，来评价本文算法的性能。参与比较的算法包括：(1)零空间追踪(NSP)算法；(2)本文算法；(3)文献[16]提出的加入正弦掩膜信号的算法；(4)EEMD算法。其中，零空间追踪算法的代码从文献[17]中获得，EEMD算法的代码从文献[18]中获得，本文算法以及文献[16]算法是我们自己实现的。

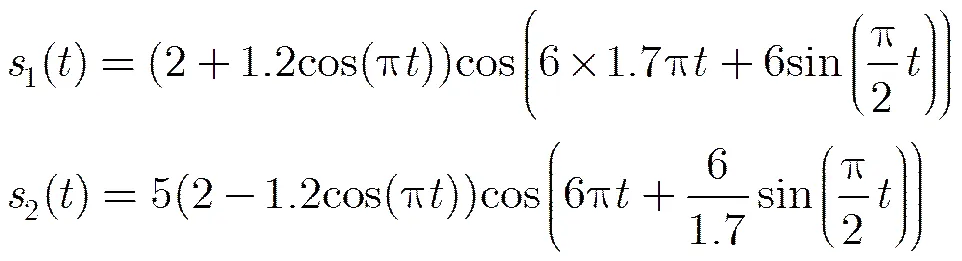
分别如图1(a)，图1(c)和图1(d)所示。图1(b)是两个子成分和的瞬时频率，可以看出两个子成分并不是全局正交的，而是局部正交的。

图2给出的是文中提出的基于算子和局部正交约束的信号自适应分解算法与零空间追踪算法的分解结果。其中图2(a)和图2(b)分别是零空间追踪算法提取的两个子成分，由图中可明显看出发生模式混叠问题：部分高频成分泄漏到低频成分中。图2(c)和图2(d)展示的分别是零空间追踪算法提取的第2个子成分的Gabor变换谱和误差信号(真实子成分减去提取的第2个子成分)。图2(e)和图2(f)分别是本文算法提取的两个子成分。图2(g)和图2(h)对应的是本文算法提取的第2个子成分的Gabor变换谱和误差信号。分解结果显示，本文算法有效地解决了这种由于能量差别大造成的模式混叠问题。

图3显示了分别采用文献[16]算法和EEMD算法对仿真信号1进行分解的结果。其中图3的第1行对应的是采用文献[16]算法提取的两个子成分，第1个子成分的Gabor变换谱和误差信号；第2行是EEMD算法的相应结果。从图中可以看出：文献[16]算法没有有效地分解仿真信号1，这是因为它采用的掩膜信号是一个频率不变的正弦波信号；EEMD算法也没有获得好的分解结果，其中算法的参数为。

仿真信号2 图4 (a)，图4(c) 和图4(d)分别展示了输入信号与其两个子成分和，其中

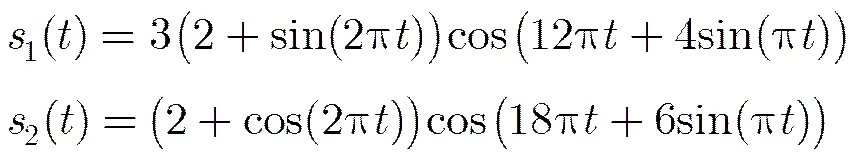
两个子成分的瞬时频率如图4(b)所示。与仿真信号1相比，仿真信号2的两个子成分具有更强的局部正交性。

图5展示了分别应用零空间追踪算法和本文算法对仿真信号2分解的结果。图5第1行分别对应零空间追踪算法提取的两个子成分，第2个子成分的Gabor变换谱和误差信号。由图中可明显看出零空间追踪算法的分解结果发生模式混叠问题。图5第2行分别展示了本文算法提取的两个子成分，第2个子成分的Gabor变换谱和误差信号。通过仿真信号2实验表明，本文算法对于子成分具有强局部正交性的信号依然能得到较好的分解结果。

图1 双分量调幅调频信号

图2 零空间追踪算法与本文算法的分解结果比较

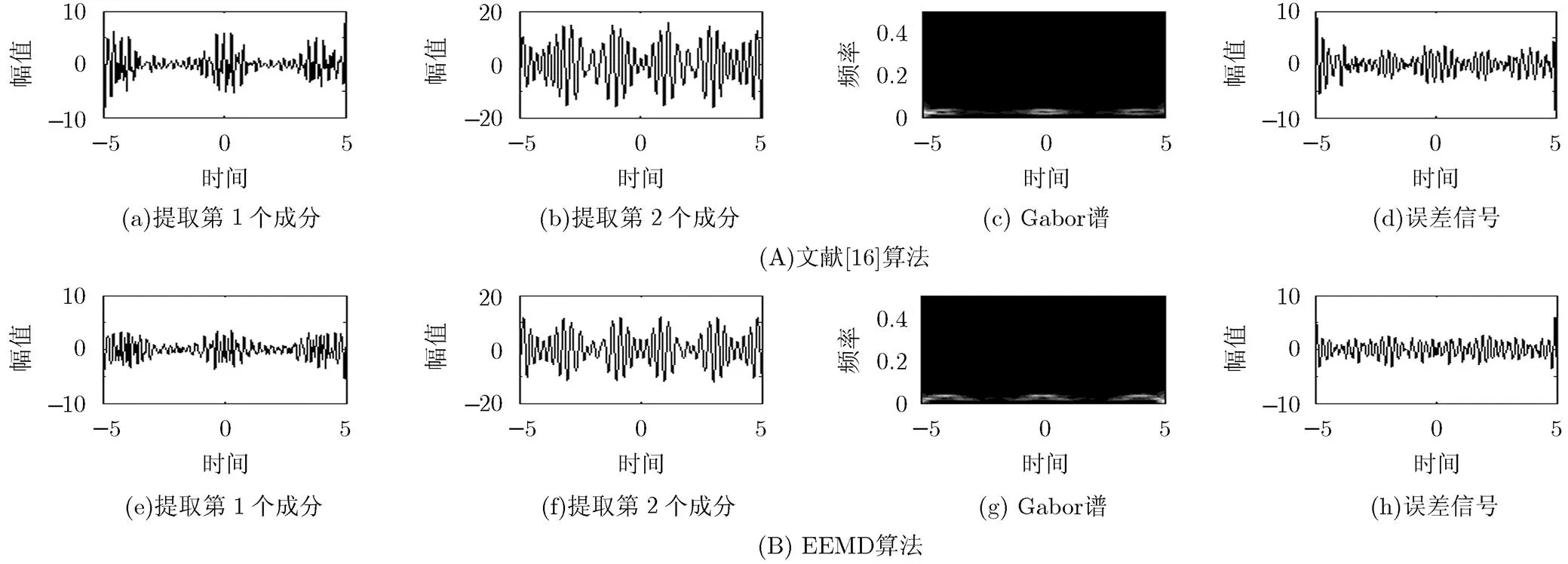
图3 文献[16]算法与EEMD算法的分解结果

图4 双分量调幅调频信号

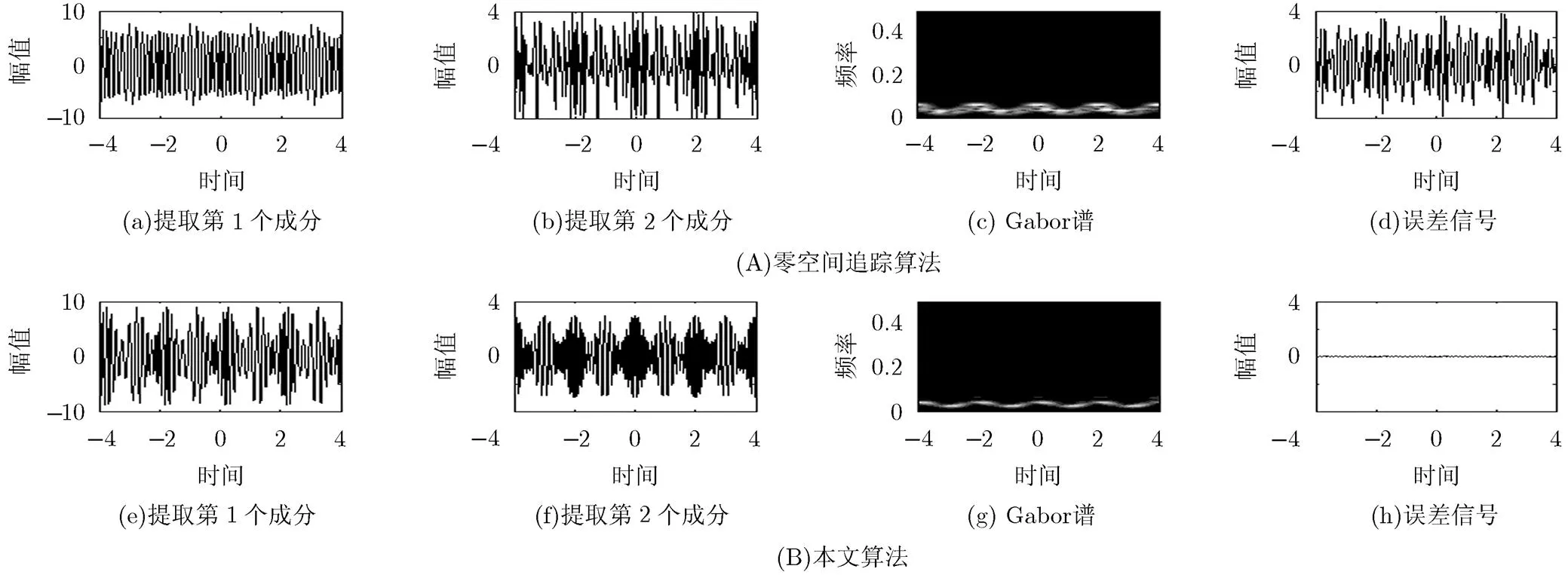
图5 本文算法与零空间追踪算法的分解结果比较

文献[16]算法与EEMD算法对仿真信号2的分解结果分别显示在图6的第1行和第2行中。EEMD算法的参数设置为。从图中可明显看出：对于具有较强局部正交性的双分量调幅调频信号，这两类算法都无法解决模式混叠问题，从而都没有获得较好的分解结果。

输入信号及其3个分量分别对应图7(a)，图7(b)，图7(c)和图7(d)。

对于多分量仿真信号3，我们首先采用零空间追踪算法(NSP)分解，提取的第1个子成分，如图8(a)所示。这个子成分明显含有剧烈的尺度变换，即发生模式混叠问题。然后采用本文算法分解输入信号，得到本文算法提取的第1个子成分，如图8(b)所示。由图明显看出图8(b)与真实子成分图7(c)非常接近，表明本文算法有效地解决了图8(a)所示信号存在的模式混叠问题。下面继续用本文算法分解剩余信号(输入信号减掉图8(b)所示的信号)，提取第2个、第3个子成分，分别如图8(c)，图8(d)所示。该实验表明，本文算法对于多分量信号也能得到较好的分解结果。

文献[16]算法与EEMD算法分解3分量调幅调频信号的分解结果如图9所示。其中第1行是文献[16]算法提取的3个子成分；第2行是EEMD算法提取的3个子成分。由图9可看出，对于调幅调频信号的分解，文献[16]算法很难得到好的分解结果。EEMD算法参数取，它对仿真信号3进行完全分解得到8个子成分，图9第2行是我们从中选出的最接近真实成分的信号，但是模式混叠问题仍然存在。

真实语音信号 我们通过一个实际的语音信号来展示本文算法的可行性和有效性。输入信号是发音为/zài/的声音经过16 kHz采样后得到的一个离散化的数字音频信号。图10(a)和图10(b)分别是输入信号和它的Gabor变换谱。

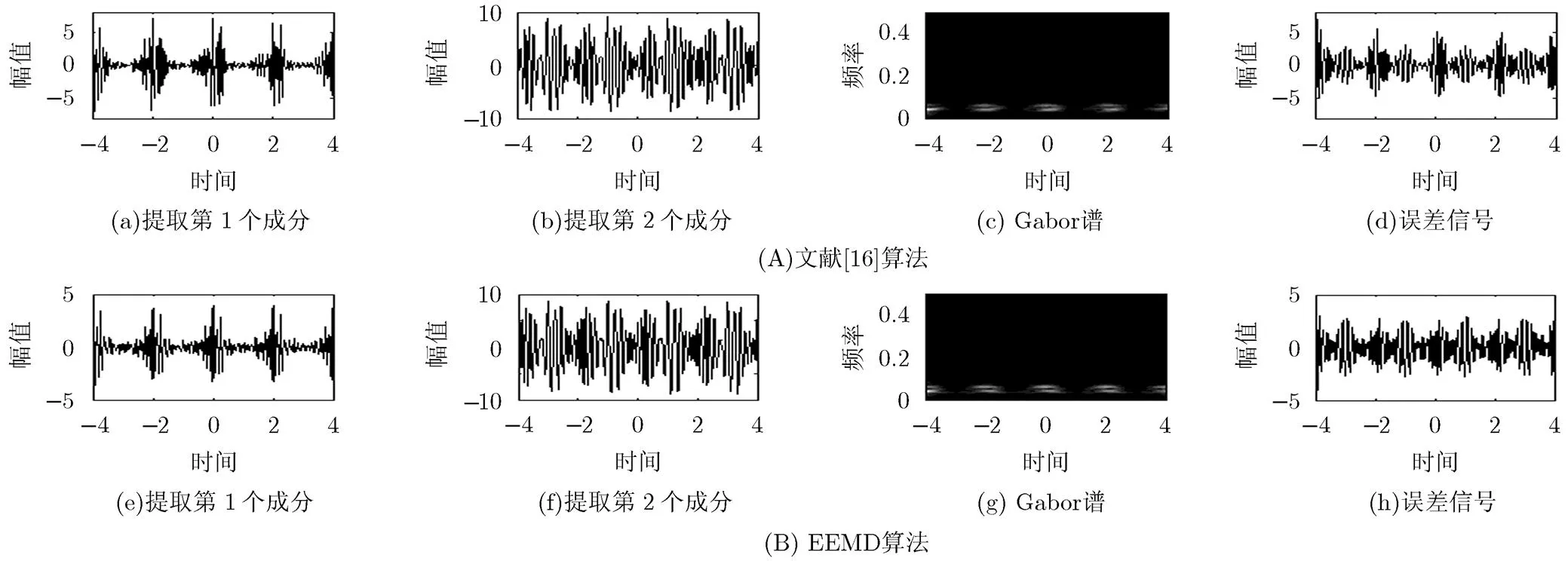
图6 文献[16]算法与EEMD算法的分解结果

图7 3分量的调幅调频信号

图8 采用本文算法解决图7(a)信号分解产生的模式混叠问题

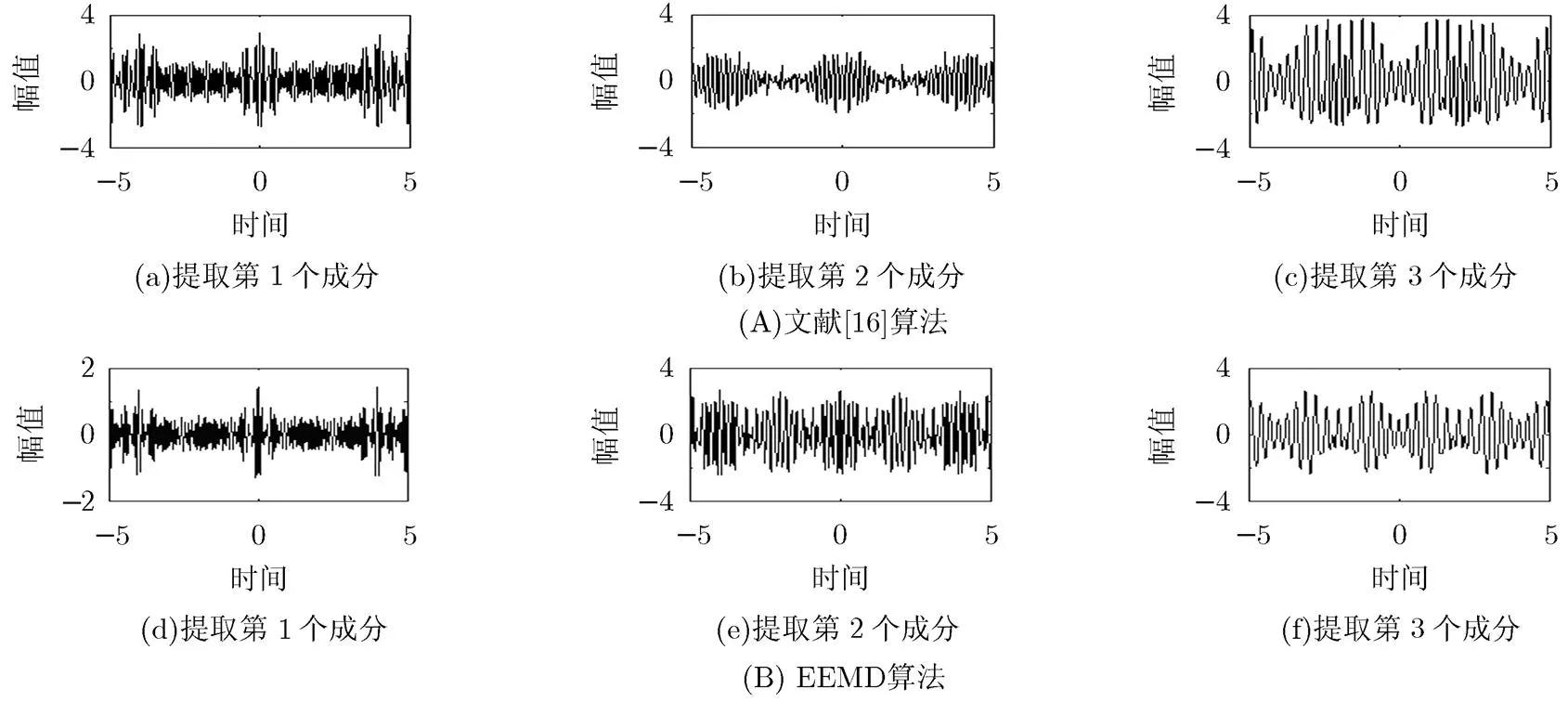
图9 文献[16]算法与EEMD算法分解3分量调幅调频信号

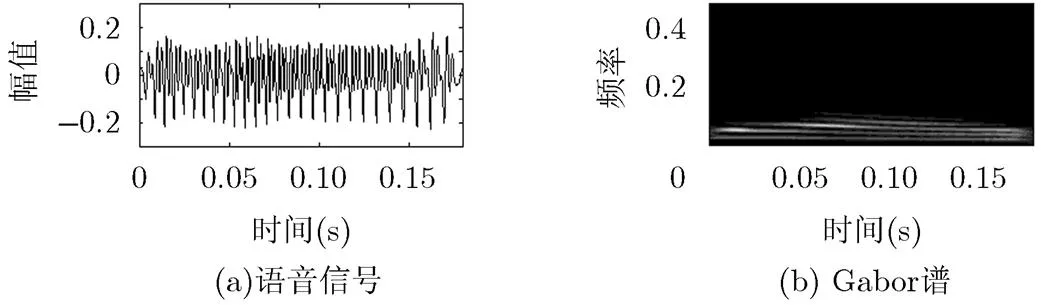
图10 真实语音信号

图11上面两行为采用零空间追踪算法分解的结果，下面两行则为采用本文算法分解的结果。从图中可以发现，下面两行的每一个分量都更加接近于一个单成分调幅调频信号。实际上，图11(i)为该声音的基频成分；图11(g)为图11(i)的倍频信号，而其余子成分分别对应于发音/z/, /a/, /i/和残差信号。由此得出，本文算法对真实语音信号分解得到了较好的结果，有效地解决了由于不同子成分之间在不同时刻存在非常大的能量差造成的模式混叠问题。

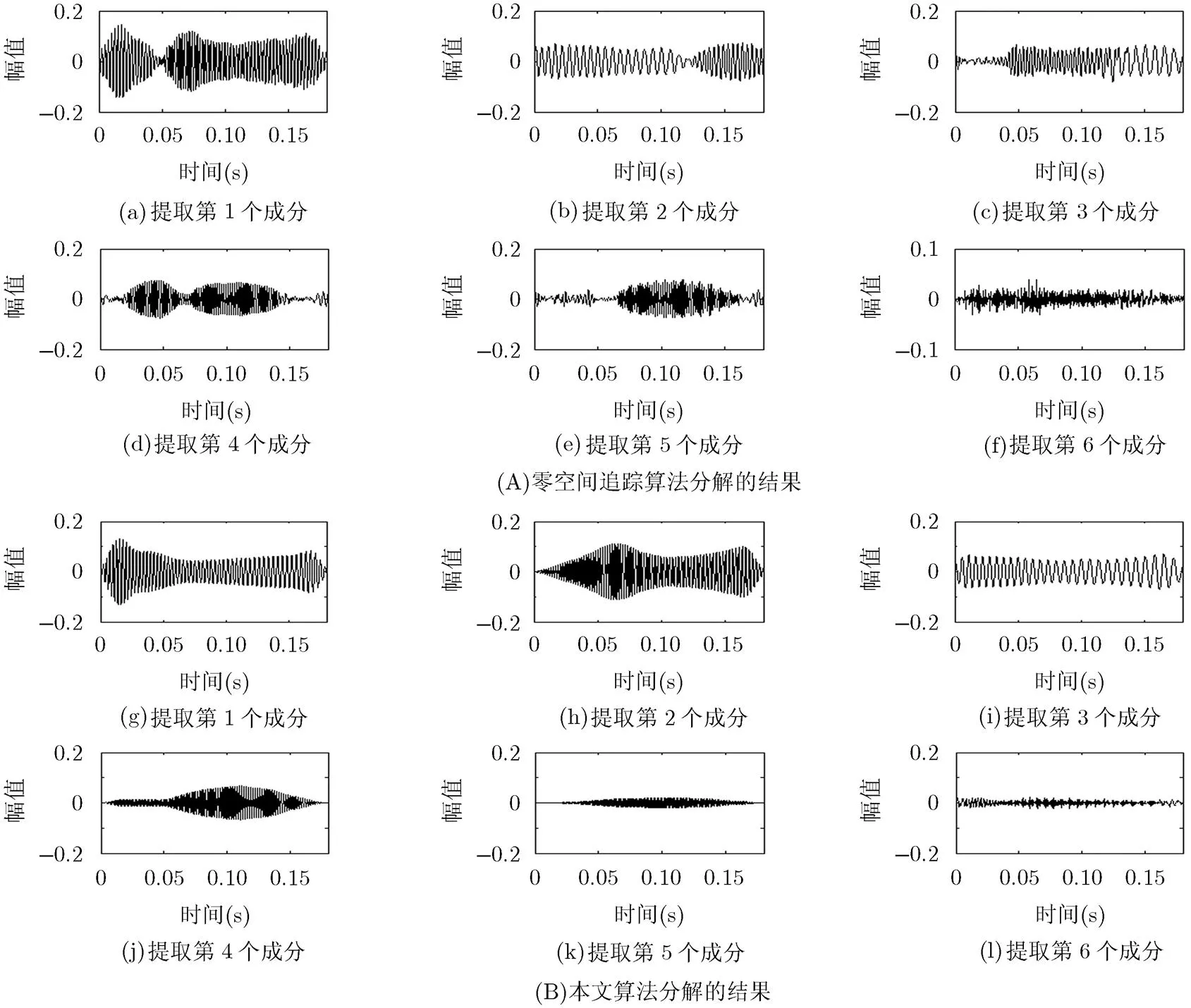
图11 零空间追踪算法与本文算法对真实语音信号的分解结果

我们采用文献[16]算法对语音信号/zài/进行分解，结果如图12上面两行所示。它依然没能获得好的分解结果，一些相似尺度的信号残留在不同的子成分中，产生模式混叠现象。EEMD算法的分解结果显示在图12下面两行，同样存在明显的模式混叠现象。这里，EEMD算法的参数设置为。无论文献[16]算法还是EEMD算法都没有有效地分解该语音信号。

4 结束语

本文针对零空间追踪算法中子成分完全正交的假设，建立了局部正交的信号模型。并利用Gabor变换，给出局部正交约束，采用反向投影策略，提出了一种基于算子和局部正交约束的信号自适应分解算法。该算法推广了零空间追踪算法[5,6]可分解信号模型的范围，有效地解决了零空间追踪算法分解信号时产生的模式混叠问题。文中采用不同的分解算法对一组仿真信号和实际真实信号进行分解，通过对实验结果的分析与比较，展示了本文算法的可行性、有效性和准确性。在下一步的研究中，将继续研究和完善零空间追踪算法，并推广其应用。

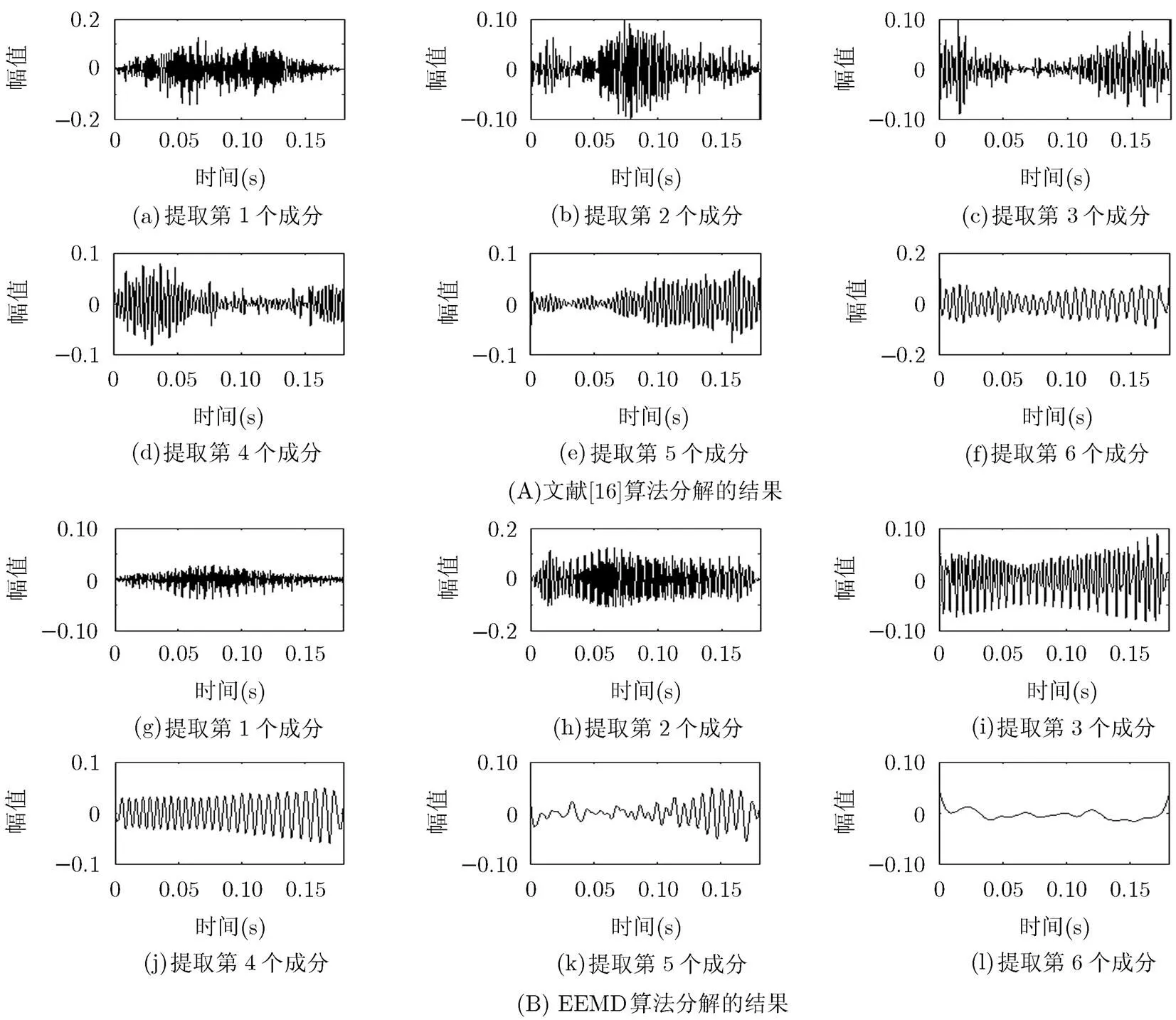
图12 文献[16]算法与EEMD算法对真实语音信号的分解结果

[1] Huang N E , Shen Z, and Long S R. A new view of nonlinear water waves: the Hilbert spectrum[J]., 1999, 31: 417-457.

[2] Yu D J, Cheng J S, and Yang Y. Application of emd method and hilbert spectrum to the fault diagnosis of roller bearings[J]., 2005, 19(2): 259-270.

[3] Pai P F and Palazotto A N. Hht-based nonlinear signal processing method for parametric and non-parametric identification of dynamical systems[J]., 2008, 50(12): 1619-1635.

[4] Huang N E, Shen Z, Long S R,.. The empirical mode decomposition and Hilbert spectrum for nonlinear and nonstationary time series analysis[J].,1998, 454(1971): 903-995.

[5] Peng S L and Hwang W L. Adaptive signal decomposition based on local narrow band signals[J]., 2008, 56(7): 2669-2676.

[6] Peng S L and Hwang W L. Null space pursuit: An operator-based approach to adaptive signal separation[J]., 2010, 58(5): 2475-2483.

[7] Mallat S and Zhang Z. Matching pursuits with time-frequency dictionaries[J]., 1993, 41(12): 3397-3415.

[8] Vese L and Osher S. Modeling textures with total variation minimization and oscillating patterns in image processing[J]., 2003, 19(3): 553-572.

[9] Bobin J, Starck J L, Fadili J M,.. Morphological component analysis: an adaptive thresholding strategy[J]., 2007, 16(11): 2675-2683.

[10] Yi X L, Hu X Y, and Peng S L. An operator-based and sparsity-based approach to adaptive signal separation[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, (ICASSP), Vancouver, BC, 2013: 6186-6190.

[11] Hu X Y, Peng S L, and Hwang W L. Multicomponent am-fm signal separation and demodulation with null space pursuit[J]., 2013, 7(6): 1093-1102.

[12] 肖维维, 栾卫军, 彭思龙. 基于三阶线性微分算子的零空间追踪算法[J]. 系统工程理论与实践, 2013, 33(5): 1283-1288.

Xiao Wei wei, Luan Wei jun, and Peng si long. Null space pursuit based on the three order linear differentialoperator[J].&, 2013, 33(5): 1283-1288.

[13] Hu X Y, Peng S L, and Hwang W L. An integral operator based adaptive signal separation approach[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, (ICASSP), Vancouver, BC, 2013: 6103-6107.

[14] Hu X Y, Peng S L, and Hwang W L. Adaptive integral operators for signal separation[J].2015, 22(9): 1383-1387.

[15] Wu Z H and Huang N E. Ensemble empirical mode decomposition: A noise-assisted data analysis method[J]., 2009, 1(1): 1-41.

[16] Deering R and Kaiser J F. The use of a masking signal to improve empirical mode decomposition[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, (ICASSP), Philadelphia, Pennsylvania, USA, 2005: 18-23.

[17] NSP codes in Matlab[OL]. http://mda.ia.ac.cn /English/ publications/publicationsindex.htm, 2010.12.

[18] Fast EMD/EEMD code[OL]. http://rcada.ncu.edu.tw/ research1.htm, 2014.9.

An Approach of Adaptive Signal Separation Based on Operator and Locally Orthogonal Constraint

Yi Xiao-lei①Peng Si-long①Luan Shi-chao②

①(,,100190,)②(-,100028,)

An operator-based approach for adaptive signal separation is proposed by using the locally orthogonal constraint and adopting back projection strategy. The approach adaptively separates a signal into additive subcomponents and a residual signal, where the subcomponents are in the null space of the operators. Experiments, including simulated signals and a real-life signal, demonstrate the feasibility, efficiency, and practicability of the proposed approach for solving the mode mixing phenomenon.

Adaptive signal separation; Locally orthogonal; Back projection strategy; Null space pursuit

TN911.7

A

1009-5896(2015)11-2613-08

10.11999/JEIT150318

2015-03-17；改回日期：2015-06-12；

2015-07-27

衣晓蕾 yixiaoleibj@163.com

国家自然科学基金(61032007, 61201375)

The National Natural Science Foundation of China (61032007, 61201375)

衣晓蕾： 女，1983年生，博士生，研究方向为信号处理.

彭思龙： 男，1971年生，博士，研究员，博士生导师，研究方向为小波分析及其在图像处理中的应用、信号处理.

栾世超： 男，1982年生，博士，工程师，研究方向为运筹学、信号处理.