基于随机纹理的代价滤波式抠图

陈秋凤 申群太 刘鹏飞②



基于随机纹理的代价滤波式抠图

陈秋凤*①申群太①刘鹏飞①②

①(中南大学信息科学与工程学院 长沙 410083)②(中国人民解放军95856部队 南京 210028)

该文针对抠图中前背景颜色歧义这一难题，提出快速随机纹理算法来对颜色信息进行有效的补偿，先对原始图像进行稠密抽取得到初始纹理，后经随机投影降维，再根据前背景交叠度选择最优通道生成随机纹理图。结合生成的纹理信息，设计了空间、颜色、纹理联合样本选择指标。接着，综合考虑局部近邻和非局部近邻的作用，对样本选择代价进行滤波。最后论证近邻迭代滤波与全局能量方程平滑的关系，推导了后期迭代平滑公式。实验结果表明，基于随机纹理的代价滤波式抠图在前背景颜色分布近似时，能够取得视觉和定量上更好的结果。

图像处理；纹理抠图；随机投影；代价滤波；迭代平滑

1 引言

计算机抠图是一项准确抠取前景的图像软分割技术，广泛应用于图像视频的编辑与合成中。尤其在多层次图像分离，半透明物体的提取中更突显其优势。抠图的建模方程为

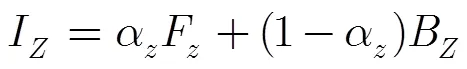
2 问题描述

步骤1 设计采样方式，采样得到待筛选样本集；

步骤2 设计样本选择指标，计算样本对选取代价；

步骤4 后期柔滑处理。本文旨在解决前背景歧义问题，以下对传统流程中存在的问题进行分析并提出解决方法，改进部分如图1中虚线框所示。

针对步骤1，本文采用文献[9]的方法；针对步骤2，主要是在样本集中，找到未知点的最优样本对。判断样本对优劣的主要指标有色度误差、距离、纹理等。现有算法中主要采用色彩和位置信息，但图像的局部统计信息可有效地补充色彩信息，在文献[6]采用的纹理算法中，首先采用两级Harr小波分解，并分别在两个层次8个子图中计算区间内的梯度、平均值、方差等一共36维的纹理信息。最后用PCA和LDA两级降维法得到3维纹理信息图。可知文献[6]算法过程复杂，运算时间长。文献[11]的纹理分类算法指出滤波器组对图像局部块的滤波操作，产生了一定的信息丢失，用图像局部原始块特征来代替传统的滤波器组输出更能有效地区分不同纹理的图像；受文献[12]纹理分类算法的启发，本文在HSV空间中，将该像素方形邻域内所有像素的特征集合作为纹理特征，首先对原始图像进行稠密抽取，再用随机投影算法对原始纹理特征进行降维，而后根据前背景交叠度选择最优通道产生3维纹理图。

针对步骤3和步骤4，传统算法采用最优者胜出原则，即代价最小的组合作为最优的样本对来计算值，而后用估计出来的值作为数据项，拉普拉斯矩阵作为平滑项构造能量函数，由于全局能量函数求解涉及高维线性方程，因而计算量大。并且当估算的值存在误差时，柔滑作用反而将错误传给邻近的点。纵观近几年抠图算法，对于最优样本对的选取策略中，代价函数的选择中并没有考虑空间连续性的指标。一个问题是：能否在最优样本的选择过程中考虑空间连续性的指标？对于近邻点对样本对的影响，文献[9]只简单地将窗口内的色度误差相加，认为窗口内的近邻的影响权重是一致的。实际上由于空间颜色信息的差别，影响值的近邻点不再局限于窗口，权重选择随着图像的变化而变化。受代价滤波式立体匹配算法[13]的启发，本文首先对样本对选择代价进行滤波，并据此选择最优样本对，有别于基本的滤波算法，文中采用广义上的近邻(局部近邻点和非局部近邻点)，并且证明代价滤波是全局优化能量方程求解过程的单步迭代。

按照改进的流程，论文安排为：3.1节论述块纹理特征抽取及随机投影降维，阐述随机纹理图求取过程及其对区分前背景的作用；3.2节设计样本选择指标；3.3节论述代价滤波对值的影响，近邻选择方法及其权重计算方式；3.4节证明迭代滤波与全局能量方程的关系；第4节为实验；第5节为结论。

3 算法实现

3.1 基于随机投影的纹理特征

图像的原始特征块能够直接有效地表征图像的纹理特征，借鉴文献[12]的块特征提取及随机压缩思想，首先对图像进行稠密抽取：图像在点抽取大小为的特征块，抽取公式为[12]

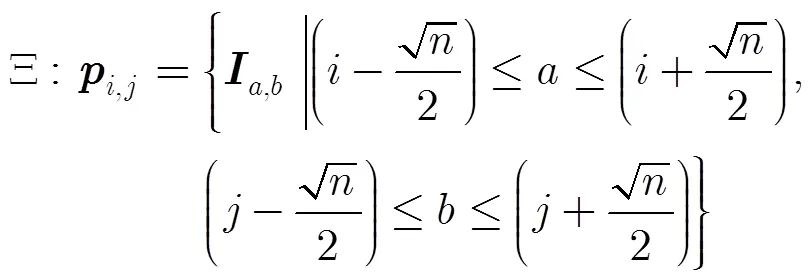
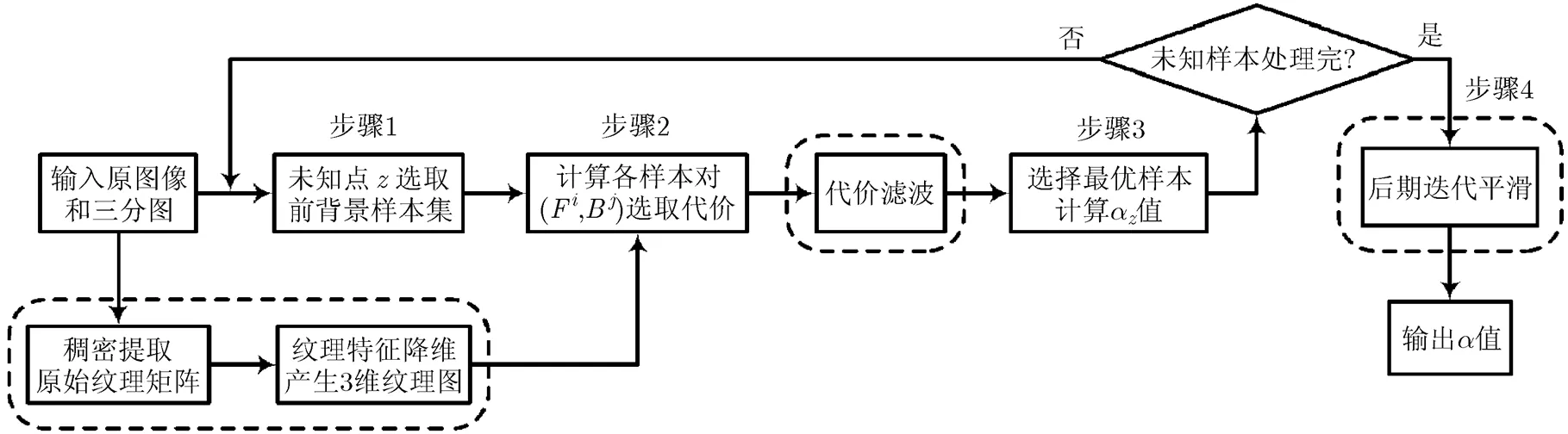
图1 算法流程图

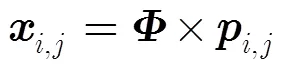
由Johnson-Lindenstrauss (L-J)定理[14]可知，当投影矩阵的元素是随机抽取自某种概率分布模型时，信号能够保持两两数据间的距离不变。这就确保了在随机投影后，纹理特征能够保持原有的内在结构，从理论上说明了随机投影压缩对纹理提取的可行性。由于抠图是提取感兴趣的前景区域，提取的纹理特征应该更加符合人的视觉特点[15]，因而首先将图像转换到HSV空间中，分别对H, S, V 3个通道进行稠密提取。扩充图像的边界区域，更换像素标号为，图像的纹理矩阵降维过程表示为

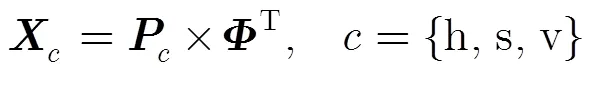
在图2中，随机算法产生的纹理图前背景颜色视觉差更大，在图3中，(a)的前背景区域颜色交叠严重(交叠度为0.64)，算法无法正确区分前背景，而文献[6]算法和随机算法前景和背景区分清楚(交叠度为0)。由此表明在根据颜色信息难以区分前背景时，纹理图像能够对原图像进行有效的补充，极大地提高前背景的区分性。虽然图3(b)与图3(c)的交叠度相同，但随机投影法的纹理分布曲线相互更加分离。而随机纹理产生过程计算简单，时间尺度为，速度比文献[6]方法有了极大地提升。例如：图2中的图像大小为，图2(b)和图2(c)的计算时间为：54.32 s和0.79 s。

3.2 采样方法与样本选择指标

首先将已知区域的边界向未知区域扩展，再用射线式方法采集待选样本集[9]，如图2(a)所示。

图2 输入图像及产生纹理图比较

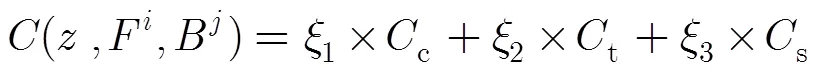
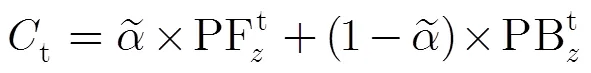
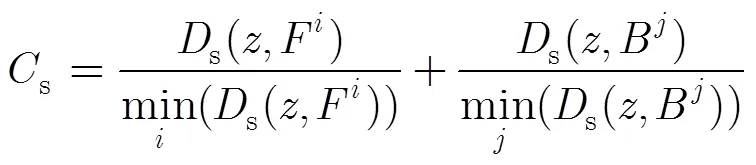
3.3 代价滤波

传统的基于能量方程综合考虑平滑作用、输入限制、采样估计输入限制及其置信度的限制，形式为[9]

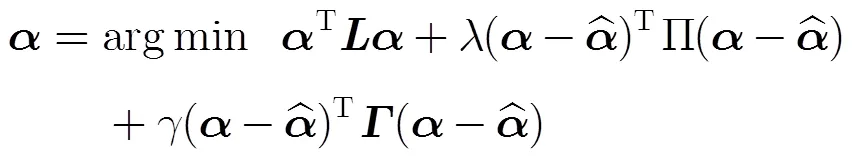
式(11)可采用图割、置信传播等方法来求解，但计算量大。在实际的抠图算法中，由于取大值，使得数据项成为影响最优解的主要部分，平滑项只实现了已知信息的小范围传播。在自然图像中，在一定的局部区域内，前背景的变化是缓慢和微小的，局部线性颜色的变化主要是由梯度的变化引起，因而用局部滤波方式代替全局能量方程的作用是可行的。代价滤波的意义在于近邻点对样本的共同适应度：一个好的样本不但要使得目标点对其代价最低，同时也需要近邻对其代价也低。

在图4(a)中，由于局部近邻点与背景点的颜色近似，代价滤波后计算的值趋向于0,有更高的概率取为背景；类似地，在图4(b)中，当近邻点与前景点的颜色近似时，值趋向于1,有更高的概率取为前景。在图4(c)中，非局部近邻点在空间上更靠近背景点，使得点的值趋向于0；同理，在图4(d)中，近邻点在空间上更靠近前景点，使得点的值趋向于1。在图4(a), 4(b)中，当未知点与近邻点空间位置近但颜色差别却很大时，即当为噪声时，局部近邻能够引导正确样本对的选择，降低噪声的影响。在图4(c), 4(d)中，当未知点与近邻点及样本对的颜色都相近时，难以区分点是倾向于前景还是背景时，由非局部近邻点的空间分布情况可以判定值的倾向性，有利于解决前背景颜色歧义问题。

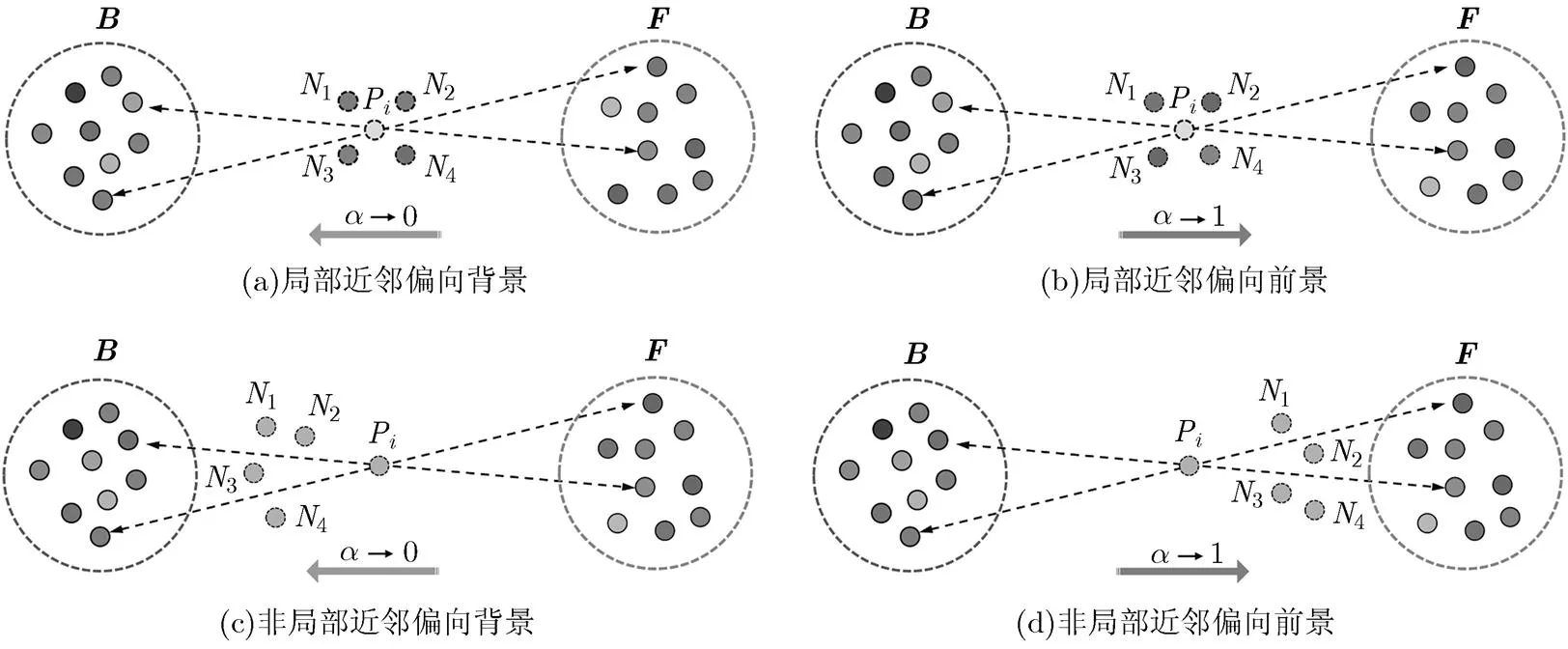
图4 近邻滤波对值的影响

在样本选择前的代价滤波操作，可以看成一个隐含的连续性指标，即最优样本的选取不仅取决于目标点，也受其近邻点的影响，避免逐点孤立地估计值，能够有效地抑制图像中噪声或是离群点的影响，从而使值更平滑。包含局部近邻和非局部近邻的代价滤波的公式为

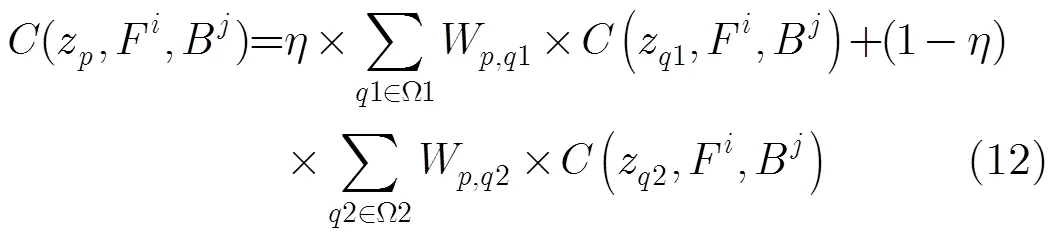
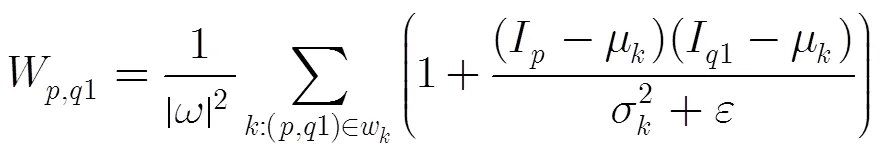
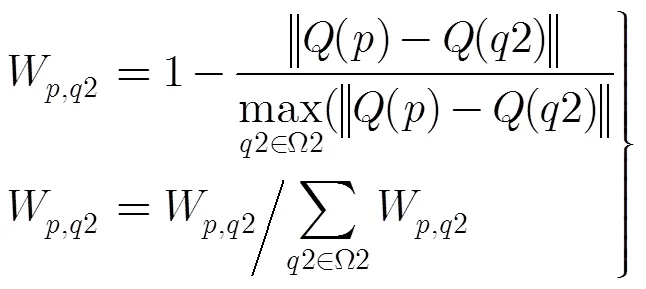
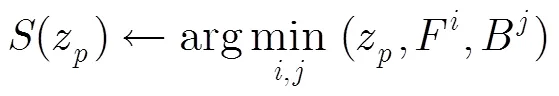
3.4 后期平滑

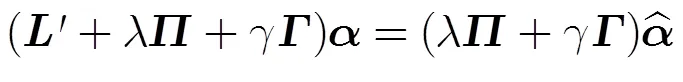
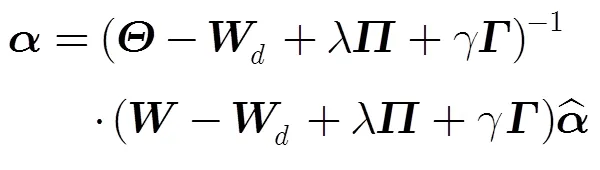
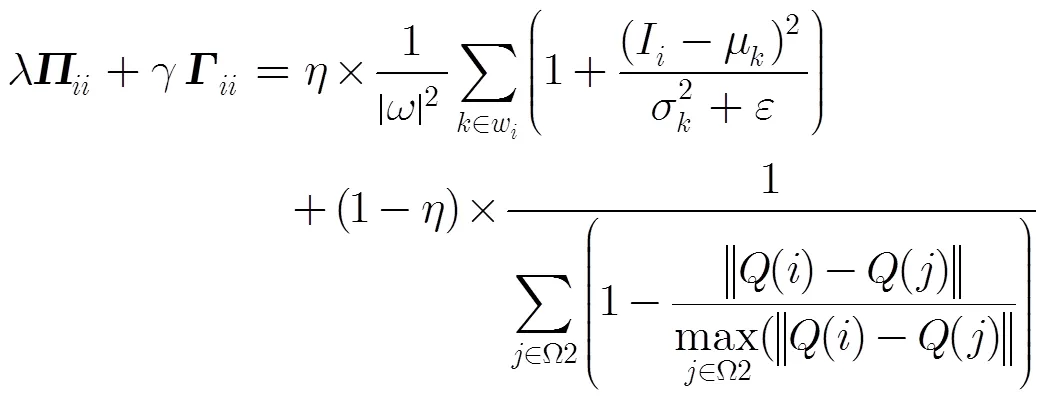
时，式(17)可简化成：

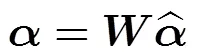
以上形式正是滤波算法的基本形式，表明滤波算法实现的是雅可比算法的单步迭代。当按式(18)取值时，输入限制权重和采样估计限制权重将发生变化，尤其是的值将大为减小，输入限制作用减弱，受到松弛输入限制。在抠图中，允许物体边缘值的改变，以获得平滑过渡的效果。

4 实验结果

实验包含：(1)与文献[6]对比，验证随机纹理方法的快速性及有效性；(2)验证代价滤波方法的有效性；(3)标准数据集上的综合测试，对比方法有：基于相似度扩散的经典算法Closed Formed Matting (CF)[1]，空间近邻采样算法Robust Matting[3]，射线式全局采样算法Shared matting[9]。标准图像数据来自文献[17]。算法的运行环境为：Intel Core i3双核3.3 G CPU，编程环境为Matlab2014。

4.1 随机投影算法的快速性及有效性

图5为文献[6]算法和随机投影算法产生的纹理图。Troll, Net, Plasticbag图像分别为：前背景近似的图像、许多孔洞的图像、高透明度的图像。与输入图像对比，纹理图像各部分可区分性增大区域整体性增强，并且能保持图像的各种细节信息，例如Troll图像的中细小的毛发，Net图像中的小洞，Plasticbag图像中的塑料袋等信息。在两种纹理图像中，文献[6]算法对边缘效果更为明显，而随机算法纹理图的区分性更大。由于纹理信息是取自图像局部块的信息，在抠图中纹理信息只作为颜色的补充，在某些情况下，文献[6]算法中过强的边缘反而不利于信息的扩散，而随机纹理图更能满足颜色补偿的需求。

图6为两种纹理算法运行时间与前背景交叠系数的对比，横坐标为27张标准图片的编号[17]。

图5 复杂图像两种纹理算法视觉效果对比

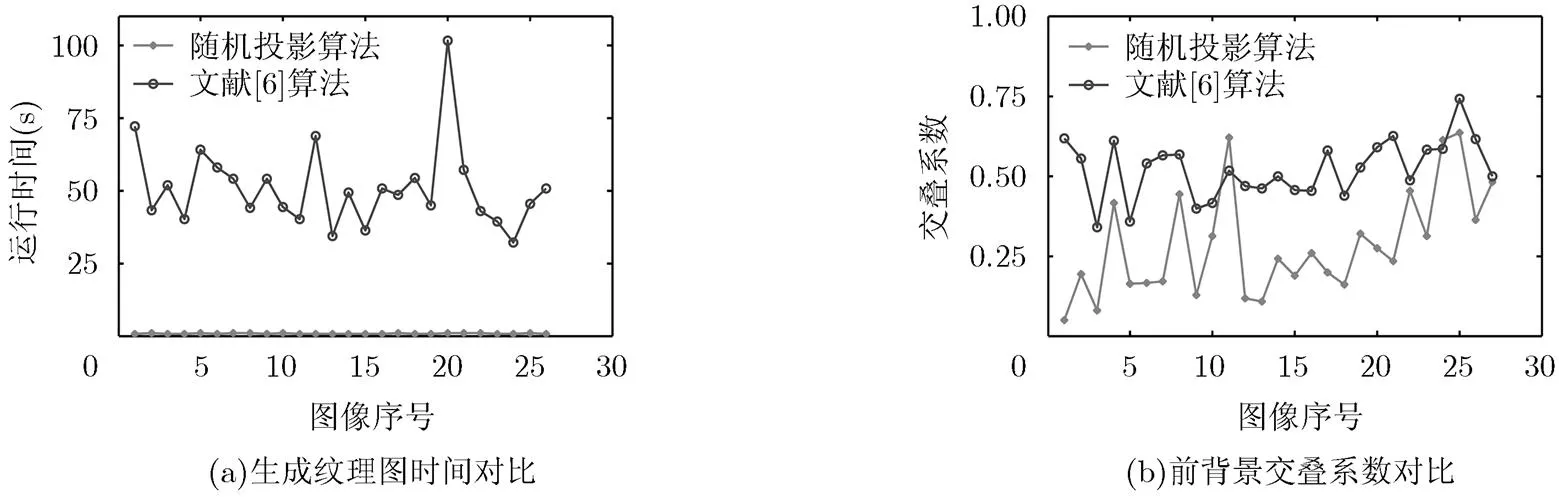
图6 文献[6]纹理算法与随机纹理算法性能对比

4.2 代价滤波的作用

在图7中，图7(a1), 7(b1)为传统Shared[9]式采样方法，图7(a2), 7(b2)为非局部和局部近邻代价滤波式方法。GT02图像为有孔洞的对象，若要正确的扣取前景，需要提供非局部近邻的信息将球外的背景信息传递到球内部，在初始的抠图结果中，传统算法由于缺少非局部近邻的作用，错误抠取背景，背景部分较代价滤波方法大，在平滑后仍然存在较大误差，而代价滤波算法在平滑后基本消除了误差。在GT06图像的抠图中，鸭子的手脚部分与背景近似容易产生粘黏，传统方法即使在后期平滑后仍存在较大的误差，而代价滤波后的方法，在平滑后基本接近真实值。

4.3 算法综合比较

在表1中，对比了3种基于采样的算法在GT02,GT13, GT19, GT26图像上的均方误差及平均绝对误差。表2为基于射线式采样的3种算法的运算时间对比。

图7 代价滤波的作用

表1各算法误差

输入图片RMSEMAE 文献[3]文献[9]本文算法文献[3]文献[9]本文算法 GT029.2e-29.2e-25.6e-23.2e-22.8e-21.9e-2 GT131.1e-11.1e-18.7e-25.0e-24.5e-23.7e-2 GT198.4e-28.4e-26.7e-23.7e-23.7e-22.4e-2 GT261.8e-11.8e-11.6e-11.0e-19.6e-27.8e-2

表2 27张标准图像平均运算时间对比

文献[6]文献[9]本文算法 运行时间(s)121.459.0717.42

从表1中可以看出，本文算法的误差最低。本文算法为了解决颜色歧义问题增加了纹理图像求取和代价滤波的计算，因而运算时间比文献[9]长，但与同样采用纹理特征的文献[6]算法相比，运算时间却小了近一个数量级。

在标准集上的测试结果如图8所示。对于文献[1]算法，由于有空间近邻的作用，抠取的结果连续性较好，但存在过平滑而产生的误差，并因其为基于局部相似度扩散的算法，无法进行远端信息扩散：如Plant图像中叶子缝隙存在的模糊区域；对于文献[3]算法和文献[9]方法，利用采样的方式虽然可以实现信息的远端扩散，但仍然无法有效地区分前背景；因而本文算法中利用随机纹理图对颜色进行补充，能够更有效地区分前背景，而且代价滤波式的采样方式比文献[9]中方法得到的效果连续性更好。

综合以上结果，基于随机纹理特征的代价滤波式抠图算法，在增加少量运算时间的情况下，在处理复杂图像的抠图中，不但能取得更好的实际视觉效果，而且在误差上也优于其他两种算法。

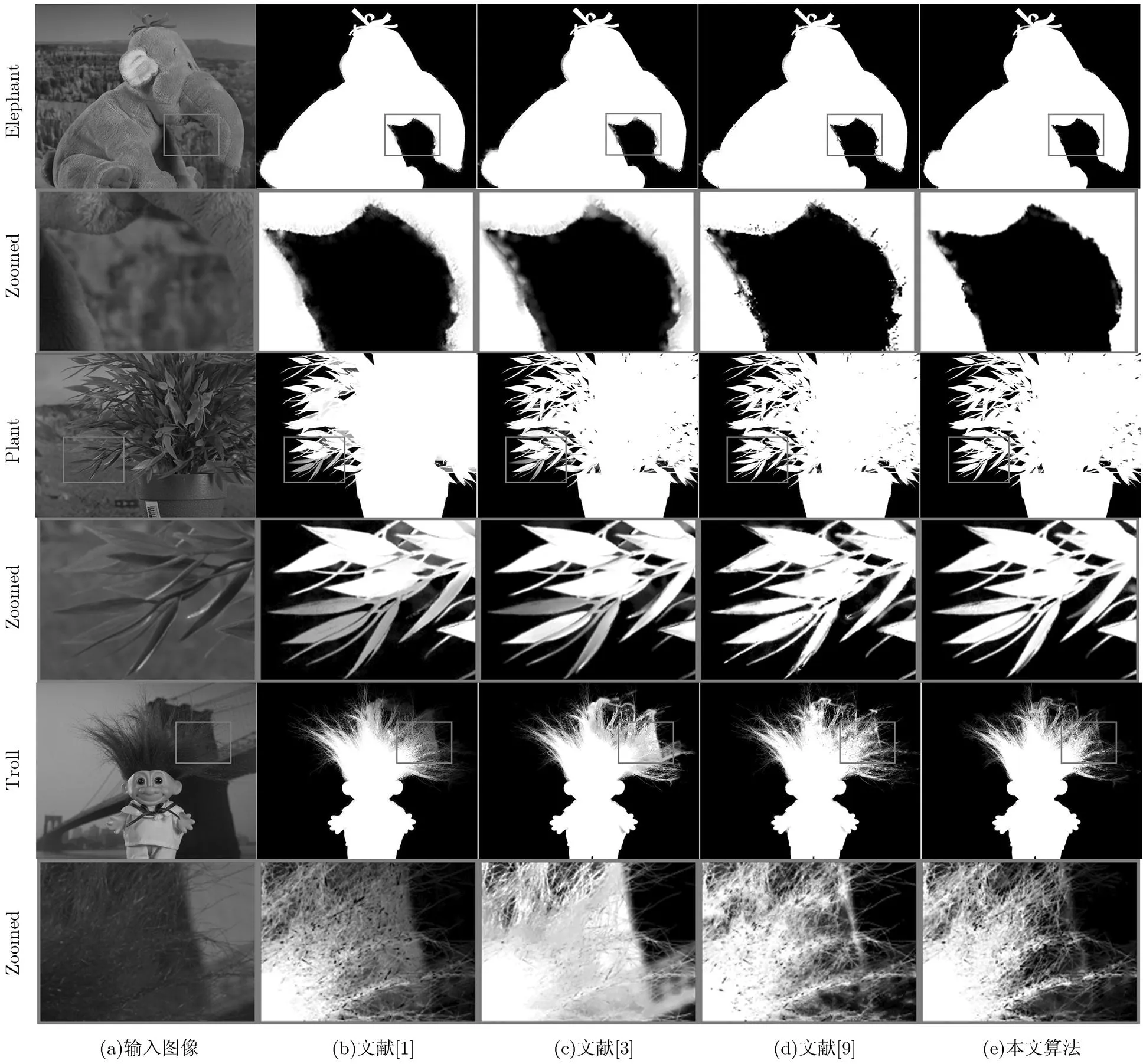
图8 复杂图像不同抠图算法结果比较

5 结束语

本文分析了传统抠图算法存在的难点，针对前背景歧义这一公开问题，提出了基于随机纹理的代价滤波式抠图算法，该算法能够快速有效地提取纹理特征，并且代价滤波式的样本选择策略能够得到更为连续性的效果，用局部迭代平滑代替全局能量函数的求解降低了算法的复杂度，实验结果表明，与其他抠图算法相比，本文算法连续性好，从直观效果和误差上都有更好的性能，能够有效地区分复杂图像的前背景。但本文计算采用统一的抽取通道数和降维数，忽略了投影矩阵的随机性，发掘抽取通道数及降维数与精确纹理方法之间的关系，以及将随机投影纹理算法应用到其他领域将是以后的进一步工作。

[1] Levin A, Lischinski D, and Weiss Y. A closed form solution to natural image matting[J]., 2006, 30(2): 61-68.

[2] Shi Y, Au O C, Pang J,.. Color clustering matting[C]. IEEE International Conference on Multimedia and Expo, California, USA, 2013, 7: 1-6.

[3] Wang J and Cohen M F. Optimized color sampling for robust matting[C]. IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, USA, 2007, 6: 281-288.

[4] He B, Wang G J, and Zhang C. Iterative transductive learning for automatic image segmentation and matting with RGB-D data[J]., 2014, 25(5): 1031-1043.

[5] Shahrian E, Rajan D, Price B,.. Improving image matting using comprehensive sampling sets[C]. Conference on Computer Vision and Pattern Recognition, Oregon, Portland, USA, 2013, 6: 636-643.

[6] Shahrian E and Rajan D. Weighted color and texture sample selection for image matting[C]. IEEE Conference on Computer Vision and Pattern Recognition, Rhode Island, USA, 2012, 6: 718-725.

[7] Rhemann C, Rother C, and Gelautz M. Improving color modeling for alpha matting[C]. The British Machine Vision Conference, Leeds, UK, 2008, 9: 1155-1164.

[8] He K, Rhemann C, Rother C,.. A global sampling method for alpha matting[C]. IEEE Conference on Computer Vision and Pattern Recognition, Colorado, USA, 2011, 6: 2049-2056.

[9] Gastal E S and Oliveira M M. Shared sampling for real‐time alpha matting[J]., 2010, 29(2): 575-584.

[10] Jubin J, Deepu R, and Hisham C. Sparse codes as alpha mattes[C]. The British Machine Vision Conference, Nottingham, England, 2014, 9: 1-11.

[11] Varma M and Zisserman A. A statistical approach to material classification using image patches[J]., 2009, 31(11): 2032-2047.

[12] Liu L and Paul W. Texture classification from random features[J]., 2012, 34(3): 574-586.

[13] Hosini A, Bleyer M, Rother C,.. Fast cost-volume filtering for visual correspondence and beyond[J]., 2013, 35(2): 504-511.

[14] Dasgupta S and Gupta A. An elementary proof of a theorem of Johnson and Lindenstrauss[J]., 2003, 22(1): 60-65.

[15] Sural S, Qian G, and Pramanik S. Segmentation and histogram generation using the HSV color space for image retrieval[C]. International Conference on Image Processing, New York, USA, 2002, 2: 589-592.

[16] Marius M and David GL. Fast approximate nearest neighbors with automatic algorithm configuration[C]. International Conference on Computer Vision Theory and Applications, Lisbon, Portugal, 2009, 2: 331-340.

[17] Rhemann C, Rother C, Wang J,.. A perceptually motivated online benchmark for image matting[OL].http://www.alphamatting.com. 2009, 5.

Cost Filtered Matting with Radom Texture Features

Chen Qiu-feng①Shen Qun-tai①Liu Peng-fei①②

①(,,410083,)②(95856,210028,)

In order to deal with the color overlap problem in matting, a fast random projection method is proposed to complement the color information. First, the raw texture matrix is obtained through dense abstraction from color image. The random projection is performed and the best three texture channels are chosen by the foreground and background overlap factors. Combining the texture image, the new cost function takes into account texture, color, and spatial information. Second, the filtering process is carried out to the sample selection cost, including the effect of the local and nonlocal neighbors. Finally, the relationship between iterative filter and global energy smooth is proven, and the post filter formula is obtained. Experiments show that the cost filtered matting with random texture features produces both visually and quantitatively better results when the color distributions of the foreground and background are similar.

Image processing; Texture matting; Random projection; Cost filtering; Iterative smooth

TP391

A

1009-5896(2015)11-2578-09

10.11999/JEIT150143

2015-01-27；改回日期：2015-06-29；

2015-08-27

陈秋凤 chenqiufeng0204@126.com

国家自然科学基金(61473318, 60974048)

陈秋凤： 女，1983年生，博士生，研究方向为图像处理、智能信息控制等.

申群太： 男，1944年生，教授，博士生导师，研究方向为智能信息处理、工业控制等.

刘鹏飞： 男，1981年生，博士生，研究方向为制导武器识别与控制、武器装备优化保障等.

The National Natural Science Foundation of China (61473318, 60974048)