基于时序特性的自适应增量主成分分析的视觉跟踪
2015-10-14蔡自兴余伶俐
蔡自兴 彭 梦 余伶俐
基于时序特性的自适应增量主成分分析的视觉跟踪
蔡自兴 彭 梦*余伶俐
(中南大学信息科学与工程学院 长沙 410083)
当前基于增量主成分分析(PCA)学习的跟踪方法存在两个问题,首先,观测模型没有考虑目标外观变化的连续性;其次,当目标外观的低维流行分布为非线性结构时,基于固定频率更新模型的增量PCA学习不能适应子空间模型的变化。为此,该文首先基于目标外观变化的连续性,在子空间模型中提出更合理的目标先验概率分布假设。然后,根据当前跟踪结果与子空间模型之间的匹配程度,自适应调整遗忘比例因子,使得子空间模型更能适应目标外观变化。实验结果验证了所提方法能有效提高跟踪的鲁棒性和精度。
视觉跟踪;主成分分析;增量子空间学习;遗忘因子;自适应增量
1 引言
视觉跟踪可以看成在连续的视频序列中根据目标运动模型和目标外观模型,寻找置信度最大的候选图像区域。在现实环境中目标物的外观通常受到光照变化、目标姿态变化、目标大小变化以及部分遮挡等因素的影响,因此如何建立一个具有增量学习能力的外观模型成为跟踪的最重要问题。目前已有的基于外观模型学习的跟踪方法主要分为3大类,基于生成模型的跟踪方法、基于判决模型的跟踪方法,以及基于生成模型和判决模型相结合的跟踪方法[8,9]。生成模型的优点是能够反映同类数据本身的相似度,缺点是对目标和背景的区分能力不足。判决模型的优点是反映了不同类别数据之间的差异,缺点是不能反映训练数据本身的特性。在复杂的背景环境下,由于背景样本的不完备、不准确和复杂性,基于判决模型的跟踪方法很难准确建立目标和背景的决策边界。另一方面,基于生成模型的跟踪方法反映了同类样本的分布,仅仅需要足够多的目标样本就能保持非常好的跟踪精度和跟踪鲁棒性。
在图像原始的高维空间中,包含大量冗余信息以及噪声信息。主成分分析(Principal Component Analysis, PCA)将高维图像数据映射到低维子空间获取目标模板内部的本质结构特征,因此反映了目标模板在低维流行中的分布特性,减少了噪声所造成的误差。在此基础上,文献[1]提出了一种基于PCA的IVT(Incremental Visual Tracker)跟踪算法,并实时增量地更新子空间模型以适应目标外观的变化,在目标外观缓慢变化情况下的IVT算法能取得较好的跟踪性能。目前基于IVT算法的扩展研究非常多,主要集中在以下几个方面进行改进。文献[10,11]在IVT算法基础上赋予目标模板不同的权值,强调目标模板对于子空间构造的不同影响程度。文献[12]采用加权平均方式融合IVT算法和基于稀疏表达跟踪算法的跟踪结果。文献[13]使用增量PCA方法构建子空间的基向量作为稀疏字典中的目标模板,然后利用稀疏表达的分类能力进行跟踪。文献[14]基于SIFT特征将图像分成若干区域,然后使用IVT算法进行跟踪。文献[15,16]首先通过色彩、纹理、灰度、梯度方向直方图等特征分别使用IVT算法进行跟踪,然后融合多特征的跟踪结果和子空间模型。
但是IVT及其所有改进的算法中存在以下两个缺点:(1)这些方法都是基于低维子空间模型来计算候选目标的相似度,没有充分考虑到目标变化的时间连续特性。因此一旦目标外观发生突变或者相似背景时,容易跟踪失败。(2)当目标外观的低维流行分布为非线性结构或者局部线性结构时, IVT算法按照固定的遗忘比例因子对线性子空间模型更新,显然不能满足复杂目标外观变化下的鲁棒跟踪需求。对原有知识遗忘过快会降低子空间模型对目标外观描述的精确性,对原有知识遗忘过慢则会降低子空间模型的适应性。
针对以上两个问题,本文在IVT算法的基础上提出了改进方法。首先针对IVT算法的观测模型的不足,基于子空间模型中目标外观的变化,本文提出更合理的目标的先验概率分布假设。其次,为了能适应目标外观变化,本文根据当前跟踪结果与子空间模型之间的符合程度,自适应调整遗忘比例因子,使子空间模型更新频率能适应目标外观变化的频率,提高了子空间模型对当前时刻目标物外观的描述能力。
2 IVT算法的基本介绍
IVT算法是基于增量子空间的粒子滤波跟踪算法,将视觉跟踪问题看成一个隐马尔科夫模型。设状态变量描述了视频图像中时刻的目标位置和运动参数,给定一组目标图像的观测值,是一个维图像向量。视觉跟踪的本质是基于隐马尔科夫模型由观测数据估计出目标的当前状态的后验概率分布,如式(1)所示,其中为观测模型,为相邻时刻目标状态间的运动模型。

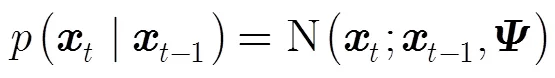
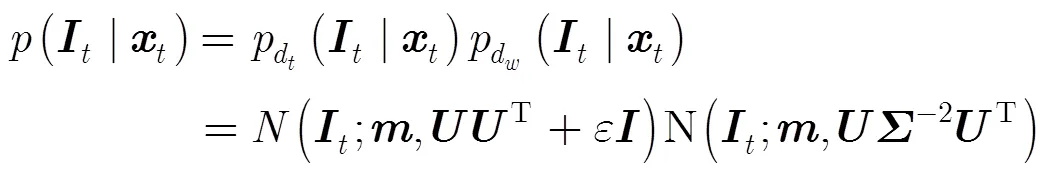
为了提高子空间模型对目标物外观变化的适应性,IVT算法采用增量更新的子空间作为目标的外观模型,在跟踪过程中有效地学习和更新目标的特征子空间。随着跟踪过程的推进,为了平衡新旧观测数据的比重,IVT算法在更新子空间模型时引入了遗忘比例因子,在每次更新子空间模型时都给先前的均值和特征值乘上一个系数。
3 本文的改进方法
本文针对IVT算法的不足进行如下改进:本文首先基于子空间模型内的目标外观变化的时序性改进了目标的先验概率分布假设,使得目标外观发生突变或者相似背景时,仍能进行鲁棒的目标跟踪,不出现发散现象。其次,本文设计了一种方法来评价当前跟踪结果与子空间模型之间的匹配程度,通过自适应调整遗忘比例因子,平衡特征子空间模型的新旧观测数据比重,使得子空间模型更能适应目标外观变化。
3.1 时序特性的观测模型
IVT算法的观测模型只关注于候选目标的相似性,而忽略了子空间模型内的目标外观变化的时间连续特性。因此本节改进了IVT算法的观测模型,把时序特性引入到观测模型中,使得目标在子空间模型内的先验概率分布假设更为合理。本文的观测模型是建立在以下两个合理假设之上的。(1)假设上一时刻,即时刻,目标跟踪的结果是可信的。(2)假设时间序列上相邻两帧跟踪结果在子空间模型上投影的变化不大。
本文提出的基于时序特性的观测模型的推导过程,如式(4)所示。首先,引入变量,根据全概率公式可以得出式(4)中的第1步推导。然后,根据文献[17]的关于PCA特征子空间中概率分布的计算原理,认为除将为的子项保留,其它对应的很小,故不予考虑,因此可以得出式(4)中的第2步推导。最后,在满足以下条件:给定,则与和相互独立;给定,和相互独立,可以得出式(4)中的第3步推导。

IVT算法的观测模型[1],如式(3)所示,只对应了新的观测模型的第1子项部分,如式(4)所示。然而目标外观的先验概率分布,即式(4)的第2子项部分被简单设置为1。因此一旦目标外观不符合子空间模型或者子空间模型对目标和背景的区分性很低时,容易跟踪失败。本文的观测模型充分考虑到目标外观变化的时间连续特性,即上述的假设(2),使用时间序列上相邻两帧跟踪结果在子空间模型上投影的差异作为子空间模型内目标外观的先验概率分布的度量准则,构建更有效的观测模型。基于子空间模型,式(4)中的和由服从高斯分布的概率密度函数可以获得[17],如式(5)和式(6)所示,其中为特征空间中心。由于在观测模型中引入了目标外观变化的时间序列特性,因此当子空间模型与当前目标外观存在偏差时或者子空间模型对目标和背景的区分性降低时,本文的跟踪方法仍然能凭借观测模型的时序特性保持鲁棒的跟踪。
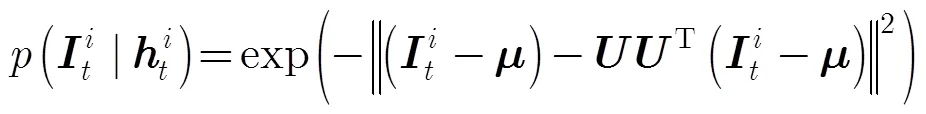
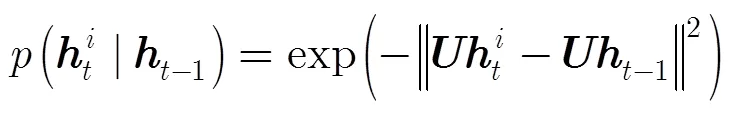
3.2 自适应调整遗忘比例因子
仅仅依靠在观测模型中引入了目标外观变化的时间序列特性(3.1节),只能在特征子空间模型还未出现较大偏差的短时间内保持稳定的跟踪。当目标外观的低维流行分布为非线性结构时,为了适应目标的外观变化,需要跟踪算法能够及时重新构建或者修正特征子空间模型。针对这一问题,当前IVT的一些改进方法采用将低维子空间模型构建成多个线性子空间模型,并且结合稀疏表达分类的原理进行目标跟踪。但是这些方法凭经验设置划分子空间的阈值,不可能满足各种目标形变和光照环境;同时多线性子空间模型增加了模型的复杂度,构建模型时容易出现过拟合。为此本文设计了一种评价子空间模型描述当前跟踪结果准确性的判决机制,通过自适应调整遗忘比例因子,平衡特征子空间模型的新旧观测数据比重,提高子空间模型对当前时刻跟踪结果的描述准确性。
基于当前跟踪结果是正确的假设前提下,评价子空间模型是否准确描述当前时刻的跟踪结果,从图像观测的角度来看本质上就是当前跟踪结果区域(即3.1节的跟踪结果)和基于子空间模型相似度最大区域之间的重叠部分的比例大小,重叠区域比例越大表明当前跟踪结果与模型之间的符合程度越高。因此本文根据使用式(4)新的观测模型估计的目标中心位置和使用式(3)原有观测模型估计的目标中心位置之间的差异,判断子空间模型的可靠性。当两者的中心位置之间的差异越大时,表明重叠区域比例越小,模型的可靠性越低,应该尽快更新模型抛弃旧样本的知识来适应目标和环境变化,所以给遗忘比例因子设置较大值;当两者的中心位置之间的差异越小时,表明重叠区域比例越大,模型的可靠性越高,应该尽量保存旧样本的知识来维持模型对目标外观描述的精确性,所以给遗忘比例因子设置较小值。
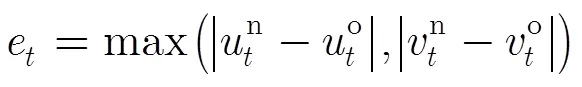
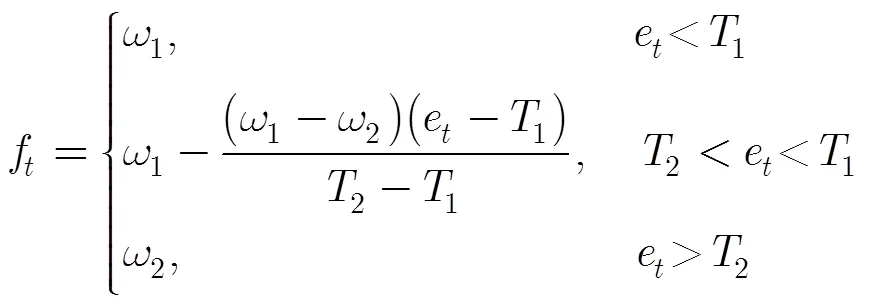
3.3 本文跟踪算法的总体框架
综合上述两节对IVT跟踪算法进行的改进(3.1节和3.2节),本文提出了一种基于时序特性的自适应增量PCA的目标跟踪算法,算法流程图见表1。其中子空间模型和子空间均值的更新具体步骤见文献[1],为候选目标的粒子权重,为粒子滤波的粒子个数。
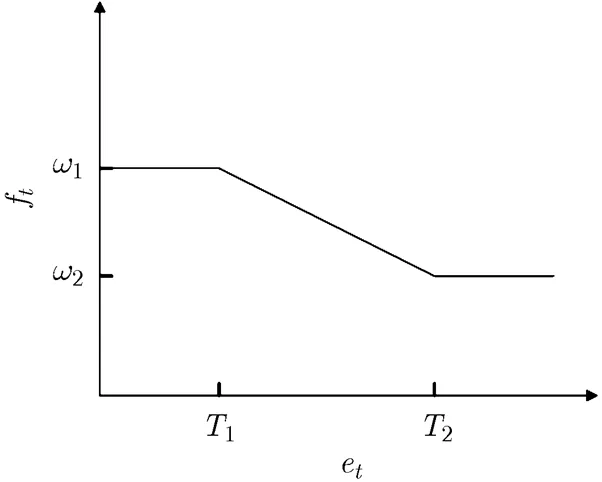
图1 遗忘比例因子和的变化关系曲线
表1本文提出的跟踪算法

输入:图像,粒子数,目标的初始状态。输出:每帧图像中目标的跟踪结果。(1)根据目标的初始状态初始化子空间模型,样本均值;(2) Fordo;(3) 根据运动模型预测当前的粒子状态,并获取对应的观测值,式(2);(4) 根据式(4)计算为目标的置信值;(5) 根据式(8)计算遗忘比例因子;(6) 取置信值最大的粒子作为跟踪结果,并根据和更新子空间模型和样本均值;(7) 根据对粒子进行重采样获取新的;(8) End for
4 实验结果及分析
为了评估本文算法执行结果,我们在多个经典的公开测试视频序列上进行了一系列的实验,并将本文算法和当前流行的经典跟踪算法IVT[1], L1APG[2]以及最新的跟踪算法MIML[7]进行了比较。这些视频中包含了各种有挑战性的情形:包括目标遮挡、光照变化、相似背景、旋转变化和尺度变化等。
本文所有算法统一将粒子数定为300个。通过仿射变化将目标区域规则化,IVT和本文算法将目标区域规则化为矩阵,L1APG算法和MIML将目标区域规则化为矩阵。
4.1 跟踪结果的定性比较
第1个测试视频Sylvester包含了光照变化和剧烈的姿态变化。如图2所示在第400, 700, 1000和1200帧比较各算法结果,IVT, L1APG和MIML算法不能适应变化而偏离了实际目标,本文算法由于考虑了目标外观变化的时间序列连续特性并且自适应调整遗忘比例因子,所以跟踪结果表现出较好的鲁棒性。
第2个测试视频Car4包含了较大的光照变化和复杂背景。如图3所示在第200, 300, 400和600帧比较各算法结果,L1APG算法不能适应变化而偏离了实际目标,IVT算法从第300帧以后都引入太多背景。本文算法由于考虑了目标外观变化的时间序列连续特性,对目标能进行更稳定而精确的跟踪。
第3个测试视频Cardark包含了剧烈的光线变化和相似背景。如图4所示在第100, 200, 300和390帧比较各算法结果,IVT和MIML算法不能适应变化而偏离了实际目标,本文的算法由于考虑了目标外观变化的时间序列连续特性,能较好地区分目标和相似背景,对目标能进行稳定而精确的跟踪。
4.2 跟踪误差的定量比较与分析
本节对跟踪误差进行定量的分析,使用了平均中心位置误差和平均重叠率作为定量分析的统计量。中心位置误差是指图像中跟踪结果的中心位置与实际值的中心位置之间的欧式距离,单位是像素。重叠率指的是跟踪结果的区域和目标真实值的区域之间的重叠部分所占的比率。表2比较了不同算法在6个经典视频中的跟踪结果的平均中心位置误差,表3比较了不同算法在6个经典视频中的跟踪结果的平均重叠率,可以看出本文算法在大部分视频中保持了较低的平均中心位置误差和较高的平均重叠率,表现出好于其它算法的跟踪精度,具有较好的跟踪鲁棒性。
IVT算法只关注于候选图像样本之间的相似性,而忽略了子空间模型内的目标外观变化的时间连续特性,并且采用固定频率更新线性的子空间模型。因此在测试视频中,当目标外观发生突变或者目标和背景不容易区分时,跟踪结果发生了严重的漂移,容易跟踪失败。
L1APG算法缺乏根据目标样本的分布准确地描叙目标流行结构的能力,区分背景和目标的能力差。并且采用基于固定阈值的模板更新策略,字典的样本更新过慢,不能适应目标外观的变化。因此在所有长时间序列的测试视频中,容易跟错目标。
MIML算法通过单一的线性映射将高维空间中的样本特征投影到低维空间进行特征提取,并且采用基于固定频率的度量空间更新策略。因此,当目标外观的低维流行分布为非线性结构时,很难构建一个有效的线性的度量空间。当发生剧烈的目标姿态变化或者遮挡时,度量空间中的距离不能准确反映候选目标的置信度,因此容易引入背景造成跟踪漂移。
本文的算法把目标外观变化的时序特性引入到观测模型,使得目标在子空间模型内的先验概率分布假设更为合理。同时,本文算法根据子空间模型和当前跟踪结果符合程度,及时进行修正子空间模型,平衡特征子空间模型的新旧观测数据比重。因此本文算法对目标能进行鲁棒而精确的跟踪。

图2 视频Sylvester跟踪结果比较

图3 视频Car4跟踪结果比较

图4 视频Cardark跟踪结果比较
表2比较不同算法在6个测试视频的平均中心位置误差(单位为像素)
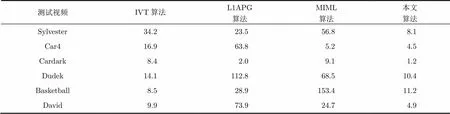
测试视频IVT算法L1APG算法MIML算法本文算法 Sylvester34.2 23.5 56.8 8.1 Car416.9 63.8 5.2 4.5 Cardark 8.4 2.0 9.1 1.2 Dudek14.1112.8 68.510.4 Basketball 8.5 28.9153.411.2 David 9.9 73.9 24.7 4.9
表3比较不同算法在6个测试视频的平均重叠率(%)
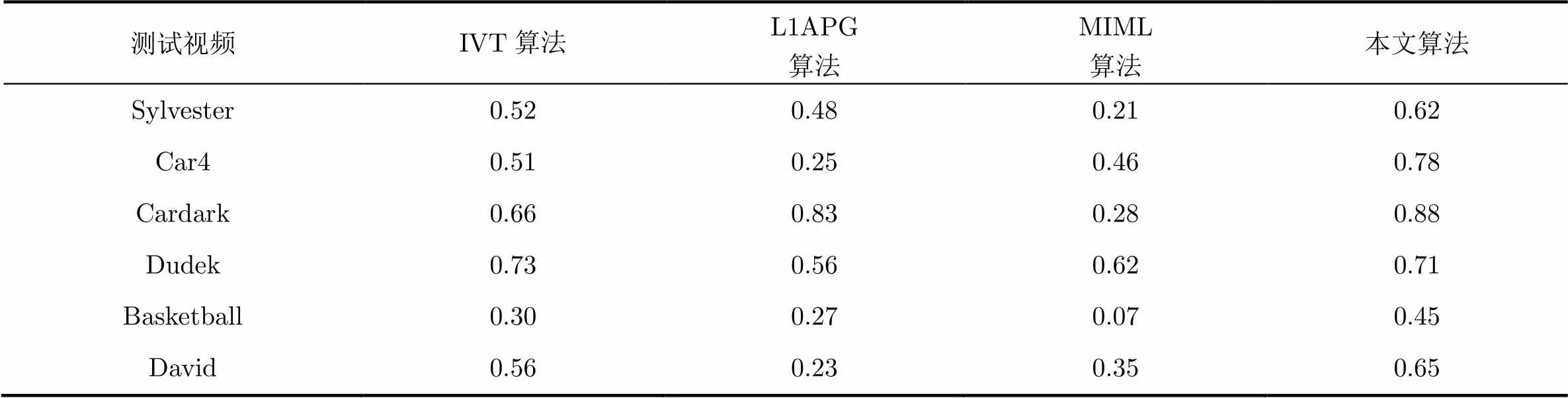
测试视频IVT算法L1APG算法MIML算法本文算法 Sylvester0.520.480.210.62 Car40.510.250.460.78 Cardark0.660.830.280.88 Dudek0.730.560.620.71 Basketball0.300.270.070.45 David0.560.230.350.65
5 结论
基于增量PCA学习的跟踪方法只关注于图像样本之间的相似性,而忽略了子空间模型内的目标外观变化的时间连续特性。为此,本文首先改进了目标的先验概率分布假设,构建更有效的观测模型。其次,为了平衡特征子空间模型的新旧观测数据比重,本文设计了一种评价子空间模型描述当前跟踪结果准确性的判决机制,通过自适应调整遗忘比例因子,提高子空间模型对当前时刻目标外观描述的准确性。因此当子空间模型与当前目标外观存在偏差时,本文的跟踪方法仍然能保持鲁棒的跟踪,适应目标外观的突变和复杂背景。实验结果定性和定量地显示本文方法能有效提高跟踪的鲁棒性和跟踪的精度。
[1] Ross D A, Lim J W, Lin R S,.. Incremental learning for robust visual tracking[J]., 2008, 77(1-3): 125-141.
[2] Bao C L, Wu Y, Linh H B,.. Real time robust L1 tracker using accelerated proximal gradient approach[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Rhode Island, 2012: 1830-1837.
[3] MeI X and Ling H B. Robust visual tracking and vehicle classification via sparse representation[J]., 2011, 33(11): 2259-2272.
[4] Babenko B, Yang M H, Belongie S,.. Robust object tracking with online multiple instance learning[J]., 2011, 33(8): 1619-1632.
[5] Grabner H and Bischof H. On-line boosting and vision[C]. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, 2006, 1: 260-267.
[6] Avidan S. Ensemble tracking[J]., 2007, 29(2): 261-271.
[7] Yang M, Zhang C X, Wu Y W,.. Robust object tracking via online multiple instance metric learning[C]. Electronic Proceedings of the 2013 IEEE International Conference on Multimedia and Expo Workshops, San Jose, 2013: 1-4.
[8] Zhong Wei, Lu Hu-chuan, and Yang M. Robust object tracking via sparse collaborative appearance model[J]., 2014, 23(5): 2356-2368.
[9] 吕卓纹, 王科俊, 李宏宇, 等. 融合Camshift的在线Adaboost目标跟踪算法[J]. 中南大学学报(自然科学版), 2013, 44(2): 232-238. Lu Zhuo-wen, Wang Ke-jun, Li Hong-yu,.. Online Adaboost target tracking algorithm combined fused with Camshift[J].(), 2013, 44(2): 232-238.
[10] 钱诚, 张三元. 适用于目标跟踪的加权增量子空间学习算法[J]. 浙江大学学报(工学版), 2011, 45(12): 2240-2246. Qian Cheng and Zhang San-yuan. Weighted incremental subspace learning algorithm suitable for object tracking[J].(), 2011, 45(12): 2240-2246.
[11] Cruz-Mota J, Bierlaire M, and Thiran J. Sample and pixel weighting strategies for robust incremental visual tracking[J]., 2013, 23(5): 898-911.
[12] Xie Yuan, Zhang Wen-sheng, Qu Yan-yun,.. Discriminative subspace learning with sparse representation view-based model for robust visual tracking[J]., 2014, 47(3): 1383-1394.
[13] Ji Zhang-jian, Wang Wei-qiang, and Xu Ning. Robust object tracking via incremental subspace dynamic sparse model[C]. Proceedings of IEEE International Conference on Multimedia and Expo, Chengdu, 2014: 1-6.
[14] Guo Yan-wen, Chen Ye, and Tang Feng. Object tracking using learned feature manifolds[J]., 2014, 118(1): 128-139.
[15] Chen Wei-hua, Cao Li-jun, and Zhang Jun-ge. An adaptive combination of multiple features for robust tracking in real scene[C]. Proceedings of the IEEE International Conference on Computer Vision, Sydney, 2013: 129-136.
[16] Yang Han-xuan, Song Zhan, and Chen Ru-nen. An incremental PCA-HOG descriptor for robust visual hand tracking[J]., 2010, 6553: 687-695.
[17] Moghaddam B and Pentland A. Probabilistic visual learning for object detection[C]. Proceedings of the IEEE International Conference on Computer Vision, Cambridge, 1995: 786-793.
[18] Chen Feng, Wang Qing, Wang Song,.. Object tracking via appearance modeling and sparse representation[J]., 2011, 29(11): 787-796.
[19] Wang Dong, Lu Hu-chuan, and Yang M H . Online object tracking with sparse prototypes[J]., 2013, 22(1): 314-325.
[20] Wang Qing, Chen Feng, Xu Wen-li,.. Object tracking via partial least squares analysis[J]., 2012, 21(10): 4454-4465.
Adaptive Incremental Principal Component Analysis Visual Tracking Method Based on Temporal Characteristics
Cai Zi-xing Peng Meng Yu Ling-li
(,,410083,)
Existing visual tracking methods based on incremental Principal Component Analysis (PCA) learning have two problems. First, the measurement model does not consider the continuation characteristics of the object appearance changes. Second, when the manifold distribution of target appearance is non-linear structure, the incremental principal component analysis learning based on fixed update frequency can not adapt to changes of subspace model. Therefore, the more reasonableprobability distribution of targets is proposed based on the continuity of the object appearance changes in the subspace model. Then, according to the matching degree between the current tracking results and the subspace model, the proposed method adaptively adjusts forgetting factor, in order to make the subspace model more adaptable to the object appearance change. Experimental results show that the proposed method can improve the tracking accuracy and robustness.
Visual tracking; Principal Component Analysis (PCA); Incremental subspace learning; Forgetting factor; Adaptive increment
TP391
A
1009-5896(2015)11-2571-07
10.11999/JEIT141646
2014-12-25;改回日期:2015-07-20;
2015-08-25
彭梦 pengmeng_pm@csu.edu.cn
国家自然科学基金重大研究计划(90820302);国家自然科学基金(61175064, 61403426, 61403423)
The Major Research Project of the National Natural Science Foundation of China (90820302); The National Natural Science Foundation of China (61175064, 61403426, 61403423)
彭 梦: 男,1978年生,博士生,研究方向为视觉跟踪和多传感器融合.
蔡自兴: 男,1938年生,教授,博士生导师,研究方向为人工智能、智能控制、机器人.
