基于Monte Carlo方法的释光测年剂量率误差估计

彭俊 董治宝 张正偲



基于Monte Carlo方法的释光测年剂量率误差估计

彭俊 董治宝 张正偲

（中国科学院寒区旱区环境与工程研究所 兰州 730000）

在释光年代学上，剂量率代表样品埋藏过程中单位时间内吸收的辐射剂量，其估计直接影响到埋藏年代的可靠性。误差传递公式(Quadratic propagation of uncertainty)常用于剂量率误差估计。由于计算剂量率涉及到众多参数复杂的非线性运算，造成基于误差传递公式的误差估计过程繁琐复杂。本文以粗颗粒石英矿物为例介绍了剂量率计算过程及误差估计方法，使用蒙特卡罗误差传递法(Monte Carlo error propagation)模拟了剂量率计算过程中多参数不确定性耦合误差，编写了执行随机剂量率模拟运算的开源程序，并通过实测数据展示了该技术的应用。相对于应用误差传递公式法估计剂量率误差，Monte Carlo方法具有直观灵活、简便科学的特点，这种随机策略在分析科学领域具有广泛的适用性。

释光测年，剂量率计算，误差传递，蒙特卡罗技术

剂量率是指样品单位时间内吸收的辐射剂量。矿物颗粒在埋藏过程中吸收的辐射剂量主要来自分布于其周围（或自身携带）的放射性核素(Radioactive nuclides)。石英矿物吸收的辐射剂量主要来自外部环境，其内部放射性核素浓度水平可以忽略[1−2]。产生放射性辐射的元素主要包括铀(235U与238U)、钍(232Th)、钾(40K)以及少量的铷(87Rb)等。除此之外，地球外部空间的宇宙射线(Cosmic rays)中的γ射线对样品剂量率的贡献也不可忽略（取决于采样地点的地理位置及样品埋藏深度）。与第四纪沉积物释光测年上限（约两百万年）相比，这些放射性核素的寿命高达109a量级，因此它们对样品剂量率的贡献可看做常量[3]。剂量率计算涉及到众多变量之间复杂的非线性转换，误差来源既包括实测误差，也包括既定误差。前者指与被分析样品有关的测量误差如铀、钍、钾、水含量误差及野外采样测定的埋藏深度、海拔高度、经纬度误差等，后者主要包括放射性核素含量与α、β、γ辐射剂量率之间转换系数（转换因子）误差，以及α、β辐射的衰减效应校正误差等。

实验室常用假定自变量参数相互独立的误差传递公式估计剂量率误差，需要计算误差函数对不同参数的偏导数，进而确定自变量参数误差对目标变量误差的贡献。另一种误差估计方法为蒙特卡罗(Monte Carlo)误差估计法，与误差传递法相比，该方法的优点主要体现在：(1) 可以直接对剂量率计算过程进行随机模拟，无需通过复杂的求导公式来确定自变量参数误差项的分析表达式；(2) 它能利用大量随机重复模拟试验获得目标变量的频率分布，全面地监测计算过程中多参数耦合不确定性导致的剂量率误差变化；(3) 对剂量率误差贡献较小的自变量参数，可依需要在模拟过程中将其设为随机值或定值，增加了多变量耦合不确定性模拟的灵活性。以下首先以粗颗粒石英矿物为例，介绍了剂量率计算方法及误差传递公式在剂量率误差估计中的应用。然后使用Monte Carlo技术模拟了多变量不确定性导致的剂量率误差传递过程，并使用程序语言编写了基于Monte Carlo误差传递过程的剂量率模拟计算开源函数calDA()。

1 剂量率计算

1.1 放射性核素对剂量率的贡献及其计算

放射性核素是指能够自发地从不稳定原子核内部释放射线或粒子从而衰变到稳定状态的元素，它携带的能量是以α、β、γ射线的形式释放。放射性辐射在穿透矿物颗粒时因所携带的能量被颗粒外层吸收，造成到达颗粒内部的能量减少的现象称为衰减效应(Attenuation effect)。因不同射线的穿透能力不同，它们的衰减效应也存在显著差异。α粒子的辐射能力仅限于距辐射源最大30 μm的范围内，粗颗粒（粒径大于90 μm）石英矿物的最外层吸收α辐射部分会在实验前处理中被氢氟酸所刻蚀，因此无需考虑α剂量率的影响。γ辐射的穿透距离高达零点几米，对不同粒径样品颗粒其能量衰减效应皆可忽略不计。β粒子的贯穿距离为几毫米，在计算β剂量率时需要依不同样品粒径对其衰减效应加以校正[4−5]。图1为矿物颗粒外层吸收的铀、钍、钾β剂量率比重随粒径变化图（数据来自文献[5]），不同粒径β剂量率吸收比重(Absorption fraction)可使用如下线性方程描述：

(2)

(3)

式(1)−(3)是通过对粒径为50 μm、100 μm、200μm、300 μm的矿物颗粒数据[5]线性拟合得到的，U-β、Th-β、K-β分别表示铀、钍、钾β剂量率吸收比重；为样品颗粒粒径。β剂量率吸收比重的不确定性可假定具有常量相对标准误差百分比（如5%）来计算。

图1 铀、钍、钾元素的β剂量率吸收比重随样品粒径变化图

无限母质假说(Infinite matrix assumption)：假定沉积母质中的放射性核素释放的辐射剂量全部为母质内的样品所吸收，即母质内单位质量物质吸收的剂量与单位质量物质释放的剂量相等。根据该假设，放射性核素对样品剂量率的贡献由其浓度与单位浓度该核素的剂量率之积决定，由此，可使用转换因子[6]将实测的放射性核素浓度转换为对应的β、γ剂量率：

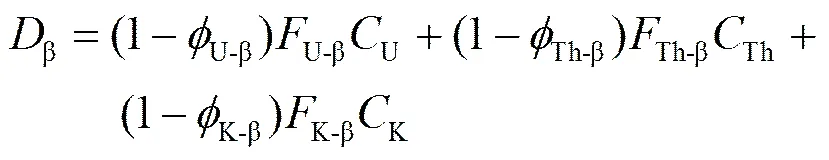
(5)

式中，β为经衰减效应校正的β剂量率；γ为γ剂量率（无需校正）；U-β、Th-β、K-β分别为样品颗粒外层吸收的铀、钍、钾元素的β剂量率比重；U、Th、K表示样品的铀、钍、钾含量（铀、钍元素含量的国际单位为mg·kg−1或μg·g−1）；剂量率转换因子U-β、Th-β、K-β、U-γ、Th-γ、K-γ的值分别为0.146、0.0273、0.782、0.113、0.0476、0.243[6]，他们的不确定性也可假定具有常量相对标准误差百分比（如5%）来获得。

1.2 宇宙射线剂量率

宇宙射线由于穿透能力强，其衰减效应可以忽略。宇宙射线剂量率是使用一系列参数根据经验公式来估算的，这些参数包括样品的埋藏深度、海拔高度、经纬度等[7]。地磁纬度()与地理经度()、纬度()之间的换算关系为[7]：

北纬与东经为正，南纬与西经为负。根据经纬度确定了地磁纬度之后，便可确定参数、、的值。图2给出了这三个参数随地磁纬度的变化关 系[7]。图2中曲线是通过对文献[7]进行矢量化提取然后使用三阶多项式拟合获得的，参数、、随地磁纬度变化的三阶多项式逼近结果为：

(7)

(9)

当地磁纬度值大于35时，可将参数、、视为定值，分别取0.231、0.761、4.098。需指出的是：采样地点地理经纬度、的不确定性会对参数、、造成影响，进而影响到宇宙射线剂量率的估计，但一般情况下这种影响可以忽略，因为通常宇宙射线剂量率对总剂量率的贡献很小，且参数、、随地磁纬度变化非常平缓(图2)。

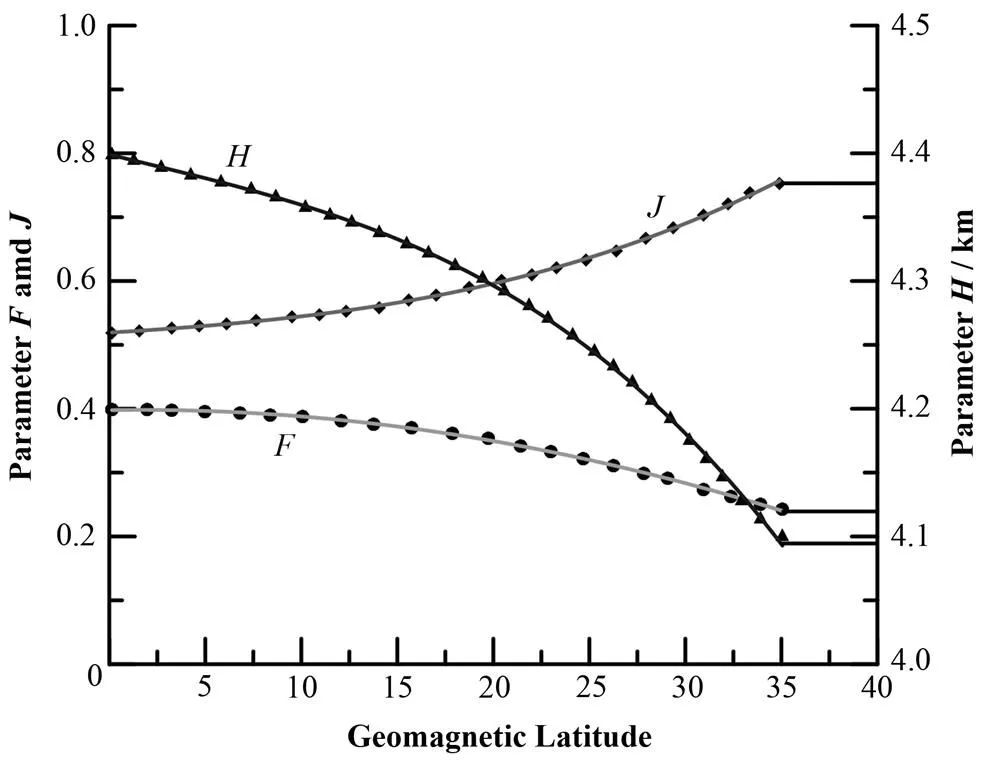
图2 参数F、J、H随地磁纬度值变化关系

因此，在估算宇宙射线剂量率误差时，可依需要选择是否并入经纬度不确定性()、()的影响。确定了参数、、之值后，宇宙射线剂量率即可通过以下公式估算[7]：

(11)

(12)

式中，是采样地点的海拔高度，m；为样品埋藏深度，m；为样品密度，g·cm−3；参数的单位为100 g·cm−2；常数=5.5×10−4。式(10)−(12)对采样深度小于104(100 g·cm−2)、海拔高度小于5×103m范围内的样品都有效。

1.3 含水量校正

水分能吸收辐射剂量，与干燥样品相比，含有一定水分样品的剂量率要相对偏低。因此，自然沉积物的剂量率需要依其实际含水量进行校正，否则会导致年龄低估。β、γ剂量率的含水量校正公式可分别表示为[8]：

(14)

式中，β、γ分别为含水量校正后的β、γ剂量率；β-dry、γ-dry分别为干样的β、γ剂量率，为实测含水量（所含水分质量与干样质量之比）。

2 剂量率的误差估计

误差传递公式是科学计算中误差估计使用最为广泛的方法[9]，以个独立自变量(x，1, 2, 3, …,)为参数的因变量函数的误差传递方程为：

式中，()为目标变量的误差；∂/∂x为函数关于第个自变量x的偏导数；2(x)表示第个自变量误差的平方。需要注意的是，由于式(15)假定自变量参数协方差为零，故仅适用于独立自变量误差分析，当某些自变量呈相关性时，该方法失效。根据式(1)−(14)的结果，粗颗粒石英矿物年剂量率方程可表示为：

(16)

式中，包含的自变量参数包括U、Th、K；U-β、Th-β、K-β、U-γ、Th-γ、K-γ；U-β、Th-β、K-β；、D等。若利用式(15)来估计剂量率的误差()，则需对所有自变量参数分别求偏导数，如目标变量对铀、钍、钾含量U、Th、K的偏导数分别为：

(18)

(19)

使用这种方法依次求出因变量对其他参数的偏导数，再根据式(15)计算不同误差项对剂量率误差的累积贡献。可见，使用误差传递公式估计剂量率误差的过程非常繁琐。此外，同样受诸多因素影响的宇宙射线剂量率的误差贡献(D)需单独估计。若忽略经纬度、及参数、、的不确定性影响，则D的误差主要取决于式(10)−(12)中参数、、的不确定性，但目标变量D对这三个参数偏导数的分析表达式同样非常复杂。

另一种不确定性估计方法为Monte Carlo误差传递法，该方法在释光测年中的应用可参考文献[10−11]。Monte Carlo技术通过大量重复性随机模拟获得目标变量的频率分布，不需进行繁琐复杂的误差解析式推导，却能全面地监测剂量率计算过程的不确定性传递。记实测铀、钍、钾含量U、Th、K误差分别为(U)、(Th)、(K)，假定剂量率转换因子及β剂量吸收比重的相对误差百分比分别为和，则相关参数值与对应的相对误差百分比之乘积即为其实际误差，如铀元素含量对β剂量率转换因子误差(U-β)U-β，铀元素β剂量吸收比重误差(U-β)U-β，由此可计算出(U-β)、(Th-β)、(K-β)、(U-γ)、(Th-γ)、(K-γ)、(U-β)、(Th-β)、(K-β)；含水量误差()取决于待测样品的沉积环境（一般可假定为5%−10%）；海拔高度误差()、埋藏深度误差()、样品密度误差()可用来计算宇宙射线剂量率误差(D)，甚至经纬度误差()、()也可以并入模拟运算中。确定了所有自变量参数的误差之后，便可假定所有参数均服从均值为给定值、标准偏差为对应误差的正态分布，例如，在软件中一组服从均值为U、标准偏差为(U)的随机铀含量数据可使用代码rnorm(=1,mean=U,=(U))生成。根据随机生成的自变量参数即可模拟计算随机剂量率值（一般需重复该过程1000−10000次），最后将模拟获得的随机剂量率数据的标准偏差作为实际剂量率的误差估计。至于对样品年龄及其误差的估计，只需在上述模拟中并入使用等效剂量及其误差()生成的随机等效剂量数据即可。本文利用软件编写了剂量率（年龄）计算与Monte Carlo误差模拟开源函数calDA()，该函数已加载到程序包numOSL[12]中，表1列出了该函数的相关参数。

表1 石英样品年剂量率Monte Carlo误差模拟函数calDA()涉及的自变量参数符号

3 计算实例

本文使用腾格里沙漠南缘风积物样品[13]的一组实测数据来说明剂量率随机模拟函数calDA()的用法。安装并加载程序包numOSL(http://CRAN. R-project.org/package=numOSL)之后，在平台中输入以下代码即可模拟剂量率计算过程：

require(numOSL)

calDA(dose=c(25.04,0.68), minGrainSize=90,

maxGrainSize=180, Ucontent=c(2.86,0.19),

Thcontent=c(8.63,0.34), Kcontent=c(2.00,0.11),

Wct=c(0.05,0.05), depth=c(1.1,0.05),

altitude=c(1170,58.5), latitude=c(37.64,1.88),

longitude=c(103.16,5.16), bulkDensity=c(2.5,0.1),

nsim=10000, rdcf=0.05, rba=0.05)

上述代码表示待分析样品的等效剂量值为(25.04±0.68) Gy，颗粒粒径为90−180 μm，铀、钍、钾含量分别为(2.86±0.19) mg·kg−1、(8.63±0.34) mg·kg−1、(2.00±0.11)%，含水量为(5±5)%，采样深度为(1.1±0.05) m，海拔高度为(1170±58.5) m，纬度为(37.64±1.88)°N，经度为(103.16±5.16)°E，样品平均密度为(2.5±0.1) g·cm−3，Monte Carlo模拟次数为10000，剂量率转换因子及β剂量吸收比重的相对误差百分比皆为5%。函数calDA()计算的样品剂量率为(3.31±0.23) Gy·ka−1，年龄为(7.56±0.56) ka，模拟生成的剂量率及年龄频率分布图见图3。这与根据误差传递公式计算的剂量率(3.29±0.24) Gy·ka−1及年龄(7.62±0.59) ka是一致的。Monte Carlo误差模拟过程具有相当高的灵活度，若希望对某自变量参数(如depth、altitude、latitude、longitude、bulkDensity、alphaValue)的误差贡献不予考虑，则模拟过程中无需提供其误差值。例如，上述代码若将海拔高度altitude=c(1170, 58.5)更改为altitude=1 170，则模拟过程中海拔高度为固定值，其误差58.5 m不参与剂量率误差模拟。

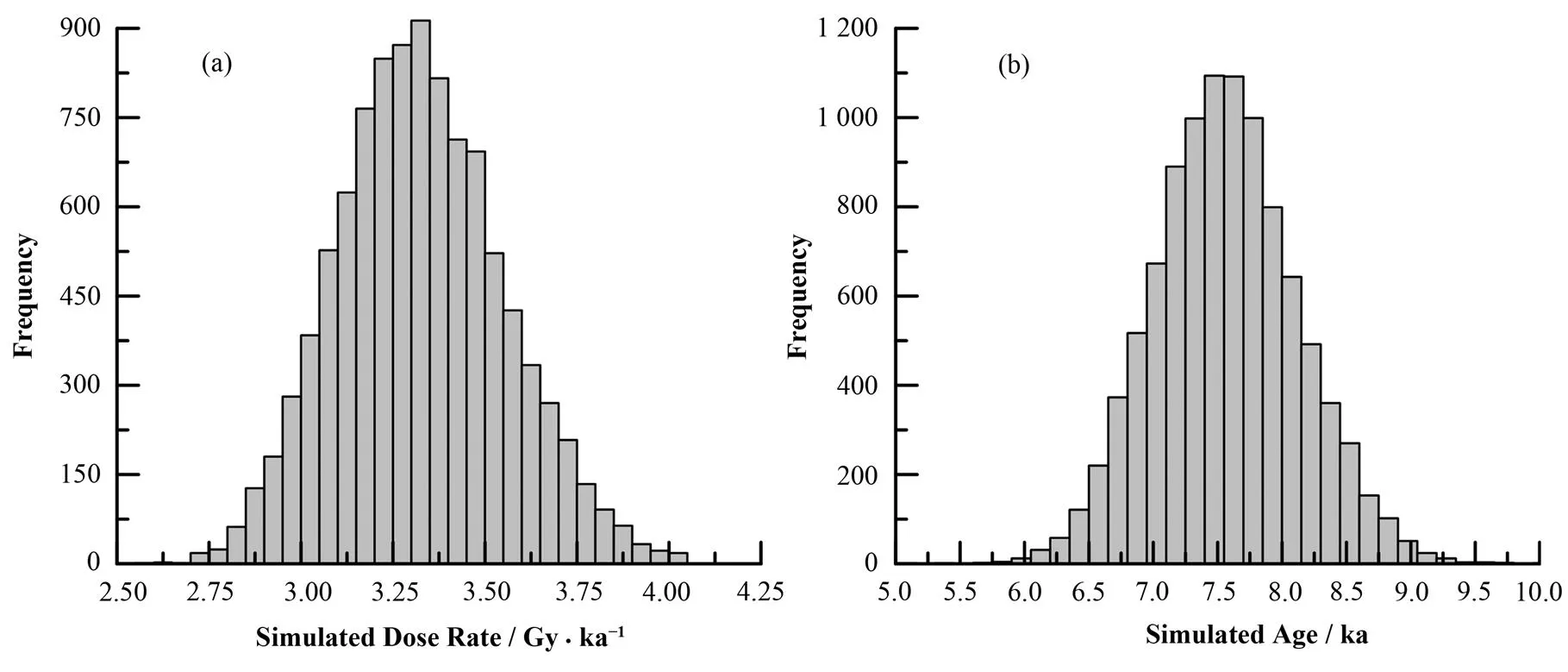
图3 Monte Carlo方法模拟的剂量率(a)及年龄(b)频率分布图

4 结语

本文介绍了释光年代学剂量率计算及误差传递法在剂量率误差估计中的应用。剂量率计算涉及的参数非常多，造成误差传递公式估计剂量率误差的过程非常繁琐。本文使用Monte Carlo误差传递技术模拟了剂量率计算的误差传递过程，并编写了执行模拟运算的开源函数calDA()。相对于误差传递公式来说，Monte Carlo误差模拟技术具有计算简便、算法灵活的特点，适用于模拟由多变量参数耦合不确定性导致的目标变量误差传递过程。

1 Murray A S, Roberts R G. Determining the burial time of single grains of quartz using optically stimulated luminescence[J]. Earth and Planetary Science Letters, 1997, 152(1−4): 163−180. DOI: 10.1016/S0012-821X(97) 00150-7

2 Zhao H, Li S H. Internal dose rate to K-feldspar grains from radioactive elements other than potassium[J]. Radiation Measurements, 2005, 40(1): 84−93. DOI: 10. 1016/j.radmeas.2004.11.004

3 Aitken M J. An introduction to optical dating[M]. Cambridge, America: Oxford University Press, 1998

4 Mejadhl V. Thermoluminescence dating: beta-dose attenuation in quartz grains[J]. Archaeometry, 1979, 21(1): 61−72. DOI: 10.1111/j.1475-4754.1979.tb00241.x

5 Fain J, Soumana S, Montret M,. Luminescence and ESR dating beta-dose attenuation for various grain shapes calculated by a Monte-Carlo method[J]. Quaternary Science Reviews, 1999, 18(2): 231−234. DOI: 10.1016/ S0277-3791(98)00056-0

6 Adamiec G, Aitken M. Dose-rate conversion factors: update[J]. Ancient TL, 1998, 16(2): 37−49

7 Prescott J R, Hutton J T. Cosmic ray contributions to dose rates for luminescence and ESR dating: large depths and long-term time variations[J]. Radiation Measurements, 1994, 23(2−3): 497−500. DOI: 10.1016/1350-4487(94) 90086-8

8 Aitken M J. Thermoluminescence dating[M]. British, London: Academic Press, 1985

9 彭子成, 袁万春, 李平, 等. ESR模式年龄误差的初步探讨[J]. 核技术, 1993, 16(4): 200−203 PENG Zicheng, YUAN Wanchun, LI Ping,. Preliminary study on errors in ESR age estimate[J]. Nuclear Techniques, 1993, 16(4): 200−203

10 Duller G A T. Assessing the error on equivalent dose estimates derived from single aliquot regenerative dose measurements[J]. Ancient TL, 2007, 25(1): 15−24

11 Peng J, Dong Z B. A simple bayesian method for assessing the standard error of equivalent dose estimates[J]. Ancient TL, 2014, 32(2): 17−23

12 Peng J, Dong Z B, Han F Q,. R package numOSL: numeric routines for optically stimulated luminescence dating[J]. Ancient TL, 2013, 31(2): 41−48

13 彭俊, 韩凤清. 腾格里沙漠南缘风积物快组分光释光信号选择研究[J]. 地球学报, 2013, 34(6): 757−762. DOI: 10.3975/cagsb.2013.06.13 PENG Jun, HAN Fengqing. Selections of fast-component OSL signal using sediments from the south edge of Tengger Desert[J]. Acta Geoscientica Sinica, 2013, 34(6): 757−762. DOI: 10.3975/cagsb.2013.06.13

Determining the error of dose rate estimates on luminescence dating using Monte Carlo approach

PENG Jun DONG Zhibao ZHANG Zhengcai

(Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences, Lanzhou 730000, China)

Background: In luminescence dating, dose rate is the irradiation dose a sample absorbed per unit time. The estimation of a dose rate affects the reliability of the burial age. Quadratic Propagation of Uncertainty (QPU) is routinely used to assess the standard error of a dose rate estimate. However, dose rate calculation involves lots of non-linear transformations between various parameters. This complicates the application of QPU method in dose rate error estimation. Purpose: In the current study, a detailed introduction to the calculation of the annual dose rate in case of coarse quartz sediments is given. A Monte Carlo technique (a “parametric bootstrap” method) is employed to simulate the propagation of uncertainty in dose rate calculation. Methods: An open sourceprogram used for performing the simulation is developed. A practical application of this technique is illustrated using a measured data set. Results & Conclusion: The Monte Carlo method is more flexible and simple in comparison with the QPU approach in dose rate error assessment. The stochastic scheme described in this article can be applied to any field of the analytical sciences.

Luminescence dating, Dose rate calculation, Error propagation, Monte Carlo technique

TL84

TL84

10.11889/j.0253-3219.2015.hjs.38.070201

国家重大科学研究计划项目(No.2013CB956000)、国家自然科学基金项目(No.41130533、No.41171010)资助

彭俊，男，1987年出生，2013年于中国科学院青海盐湖研究所获硕士学位，现为博士研究生，主要从事释光年代学研究

2015-04-01，

2015-06-01