变风量空调系统静压设定值自适应重置方法
2015-10-13代武贺张吉礼赵天怡
代武贺 张吉礼* 赵天怡
大连理工大学建筑能源研究所
变风量空调系统静压设定值自适应重置方法
代武贺 张吉礼* 赵天怡
大连理工大学建筑能源研究所
本文提出了变风量空调系统最不利热力末端和最大阀位末端的概念,研究了基于最大阀位末端目标阀位域的Mamdani模糊参考模型的静压设定值自适应重置方法。在大连理工大学空调系统智能控制综合性能试验台上,实现了送风机变静压自动控制。通过对比试验分析得出,此方法与变定静压设定值方法相比,静压设定值调整的目的性更强,调整到目标阀位域的速度更快,末端阻力损失更小,节能效果明显。
最不利热力末端 最大阀位末端 目标阀位域 Mamdani模糊参考模型 静压设定值 自适应重置方法
变风量空调系统因其能够随着负荷的变化而改变送风量的特点,在降低风机的能耗上有很大的优势,但在实际的工程应用中,由于送风静压参考变量及其控制逻辑复杂等原因,常导致系统稳定性较差,末端风量达不到设定值要求,变风量末端阀门阻力损失大等问题。目前,文献[1~2]总结了变风量空调系统送风量控制方法,包括定静压控制法、变定静压控制法、变静压控制法、总风量控制法等,每种方法都有各自的优点。其中,变定静压控制法在保持系统稳定性的同时又能够降低风机的能耗,但是此种控制方法的算法复杂,尤其是很难根据系统的负荷需求对静压设定值进行重置。因此,到目前为止,仍然缺乏实用且行之有效的方法。本文首先提出了变风量空调系统最不利热力末端和最大阀位末端的概念,然后,提出了基于最大阀位末端目标阀位域的Mamdani模糊参考模型的静压设定值自适应重置方法,最后通过试验探讨了该方法与变定静压设定值法的可行性及优越性。
1 最不利热力末端和最大阀位末端
图1为典型的某变风量空调系统原理图,图中Pset为送风静压设定值,Pa;Qseti为末端i的风量设定值,i=1,2,3,…,n,m3/h;Qsensori为末端i的风量测量值,i=1, 2,3,…,n,m3/h,δDmpri为末端i的调节阀阀位,%。图1中送风静压监测点的位置设置在距离送风机出口约2/3管段处,根据压差传感器DPT的送风静压值P与Pset的偏差通过变频器VFD来调节风机的转速,以维持P为设定值。变风量末端i通过调节阀门的开度δDmpri,来使风量测量值Qsensori达到风量设定值Qseti,而风量设定值Qseti由室内温度值与室内温度设定值的偏差来确定。

图1 典型的某变风量空调系统原理图
在具有n个变风量末端的连续调节的空调系统中,在供热或供冷工况下的某段时间内,且采用空调系统定送风温度控制,若第i个末端持续保持如下工况:
1)该末端的调节阀阀位达到全开或者接近全开的位置δDmpriMAXi(可调),即δDmpri=100%或δDmpri=δDmpriMAXi;
2)对于变风量空调系统,该末端的风量测量值Qsensori在该时段持续小于其风量设定值Qseti,导致室内温度达不到设定值。
则定义末端i为该时段系统的最不利热力末端。
关于最不利热力末端的几点说明:
1)最不利热力末端表征了变风量空调系统在实际运行中可能出现的一种不利的工况,当前末端的风量已为风阀所能调节到的最大风量,此风量下该末端向房间的供冷量(或供热量)已经出现或者即将出现无法满足该末端空调负荷需求的现象,故称为最不利热力末端。可见最不利热力末端应该是系统的调节过程中避免出现的一种情况。
2)最不利热力末端的出现表明当前送风机的工作状态已至少不能满足该末端用户的风量需求或热能供应需求,需要及时改变送风机的工作状态,如提高静压设定值,增加风机动力等。
3)在某段时间内,变风量空调系统可能同时出现不止一个最不利热力末端,且最不利热力末端所在的位置是随机变化,可能是传统的最不利环路即最不利水力环路所在的末端,也可能不是,并且与各个用户的风量设定值变化情况、管网的水力特性及风机的运行特性相关。
4)当最不利热力末端不是最不利水力环路所在的末端时,现有的以最不利水力环路末端阀门开度等变量为参考变量的送风机风量控制,对最不利热力末端来说是没有意义的,在该种工况下最不利热力末端的用户室内温度无法达到控制要求。因此,应该寻找其他的策略以实现对送风机的控制调节。
5)最不利热力末端可根据其定义通过某时间段内变风量末端调节阀的阀位、该末端风量测量值以及风量设定值等参数的状态及变化趋势来实时判断。
可见,最不利热力末端是变风量空调系统运行调节中所不希望发生的一种工况,送风静压设定值Pset的取值大小应避免最不利热力末端的出现。
在具有n个末端的变风量空调系统实际运行过程中,若某时间段内第i个末端调节阀的阀位达到所有末端中的最大值,则该末端为该时间段内变风量空调系统的最大阀位末端。
最大阀位末端是相对于所有末端的调节阀开度而言的,最大阀位末端的调节阀不一定全开。最大阀位末端的定义为预先判断最不利热力末端可能出现的位置提供了判定参考。
2 基于最大阀位末端目标阀位域的Mamdani模糊参考模型的静压设定值自适应重置方法
2.1 静压设定值重置的参考变量
静压设定值的确定需要符合以下两点要求:
1)静压设定值能够满足系统中所有末端的风量需求,以防止最不利热力末端的出现。当系统中出现最不利热力末端时,静压设定值能够及时地做出调整,使最不利热力末端的风量达到风量设定值要求。
2)由于静压设定值的大小对送风机的节能效果影响很大,因此,希望静压设定值在满足各个末端风量要求的情况下能够尽量小,体现在各个末端上就是尽可能使调节阀处于最大开度,这样既能节约风机的动力,同时又可以降低末端阀门的噪声。
综上选取最大阀位末端调节阀阀位为静压设定值重置的参考对象。
2.2 静压设定值重置的目标阀位域
在实际的变风量送风量控制系统中,为了保持送风机控制的稳定性静压设定值的调整次数不宜过多,因而静压设定值无法以某一确定阀位值为目标来进行调整,但是可以选定一个变化范围来作为目标阀位域。由于变风量末端的阀门属于等百分比流量特性,阀位越接近于全开,阀位的变化所引起的阻抗变化越小,即阀门对流量的调节作用变化越小,所以可以将具有上述特性的阀位范围[δDmprMIN,100%]作为静压设定值重置的目标阀位域,从而减少静压设定值的重置频率。
2.3 Mamdani模糊参考模型的静压设定值自适应重置方法
静压设定值的重置目的是使最大阀位末端的阀位δDmprMAX处于目标阀位域内,为了能够预判出最不利热力末端出现的可能性,该范围的上限值应该是接近100%,下限值应该略大于δDmprMIN,因此设满足该条件的δDmprMAX范围是[δRSTMIN,δRSTMAX]为目标阀位域。
1)当δDmprMAX>δRSTMAX时,最大阀位末端具有发展成最不利热力末端的趋势,为避免其发展成为最不利热力末端,此时Pset该有所提升,相应的最大阀位末端的入口静压增加,将δDmprMAX降至目标阀位域内。
2)当δDmprMAX<δRSTMIN时,最大阀位末端具有调节阀位低于目标阀位域的趋势,为避免阀位减小而导致系统的阻抗增加,此时Pset应该有所降低,将δDmprMAX升至目标阀位域内。
3)当δDmprMAX∈[δRSTMIN,δDmprMAX]时,δDmprMAX处于较理想的范围之内,既避免了最不利热力末端的出现,又使得最大阀位末端具有较低的阻抗水平,且系统在低阻抗的情况下运行,此时Pset即为理想的静压设定值。
当系统的静压值需要重置时,最关键的就是确定此时需要的静压增加值△PIn或者减少值△PDe。因此,这里使用Mamdani模糊模型[3]作为模糊规则,结合作用模糊子集推理的方法[4,5]实现△PIn和△PDe的自适应调整,称之为参考M模型的静压设定值自适应重置方法。
M模型结构为双输入,单输出,对于输入量a与b,M模型的输出量c可以表示为c=M(a,b)。根据M模型进行△PIn和△PDe的自适应调整,如式(1)和式(2)。图2为参考M模型自适应重置方法的示意图。


图2 参考M模型自适应重置方法示意图
式(1)中:δDmprMAX为最大阀位末端阀位值,%;QBOXMAX为最大阀位末端对应风量值,若系统中同时存在多个最大阀位末端,取这些末端中风量的最小值,m3/h;δD为目标阀位域的宽度,%;δRST为目标阀位域的中心,%;eδDmprMAX为δDmprMAX的偏差,即eδDmprMAX= δDmprMAX-δRST,%;ecδDmprMAX为δDmprMAX的偏差变化,当前采样时刻的eδDmprMAX与上一采样时刻eδDmprMAX的差值,%;eQBOXMAX为QBOXMAX偏差,即eQBOXMAX=QBOXSETQBOXMAX,m3/h;ecQBOXMAX为eQBOXMAX的偏差变化,即当前采样时刻的eQBOXMAX与上一采样时刻eQBOXMAX差值,m3/h。
式(2)为静压重置变化值△PIn和△PDe。
图2中,加粗实线和虚线表明了Preset的重置值所在的区域,其中加粗虚线表示△PIn和△PDe分别根据M模型、当前工况下的δDmprMAX和QBOXMAX的偏差及偏差变化对静压设定值进行自适应重置的过程。
不同形式的空调系统需要根据其负荷变化的特性对重置方法中的参数,如eδDmprMAX,ecδDmprMAX,eQBOXMAX,ecQBOXMAX,的实际论域进行优化选取。
3 静压设定值重置方法试验研究
3.1 试验系统概况
本试验平台隶属于大连理工大学中央空调智能试验系统,包括变风量空调系统的相关设备和自动控制系统。空调系统的设备包括,一台变频调速控制的离心式送风机、送回风孔板流量计、电动新风阀、电动回风阀、电动排风阀、加热盘管、三个压力无关型末端和若干不同量程和精度的压差传感器。试验台自动控制系统的硬件使用1台霍尼韦尔XL100和1台带若干扩展模块XCL8010A控制器,使用霍尼韦尔care软件实现自动控制系统的通信和控制程序。
试验原理:试验过程中关闭排风阀,送风孔板流量计和回风孔板流量计测得送风量和回风量,两者差值可以得到新风量,采用新风段静压控制法[6]控制新风量;采用压力无关型控制末端对室内温度进行控制,末端的风量和阀位信息可以通过控制器实时采集;送风机的控制首先利用采集到的末端阀位信息和风量信息确定静压设定值,然后与静压监测值比较,最后通过变频器调节风机的频率;通过调节电动连续调节阀控制进入加热盘管的水量,进而实现对送风温度的控制,试验台简化后的原理图如图3所示。
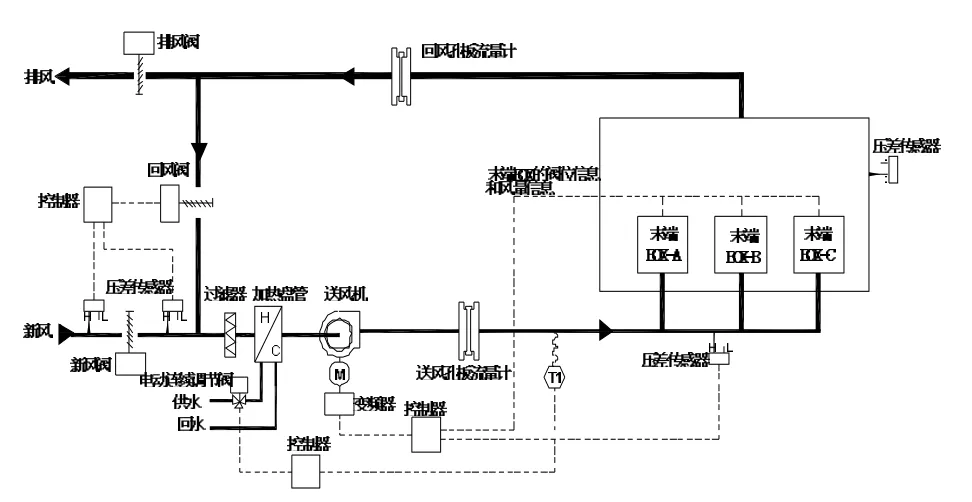
图3 参考M模型的静压设定值重置方法研究试验台原理图
3.2 静压设定值重置方法的试验程序模块
表1为程序模块采用的模糊规则表。偏差e、偏差变化ec、控制量输出u的模糊论域均取[-2,2],e与ec的论域可以划分为5个模糊等级包括“负大”、“负小”、“零”、“正小”、“正大”,分别用NB,NS,ZE,PS,PB来表示,采用的隶属函数如图4所示。图4中所列出的隶属度函数的线性表达式对应了e与ec的6个模糊子论域,模块将Fe与Fec(e与ec的模糊值)代入以上这9组线性表达式中,计算隶属度。对于一组Fe与Fec的值,模块可以计算各个作用模糊子集下的Fe与Fec的隶属度,从而实现作用模糊子集推理的方法,最后得出u对应的模糊值Fu,通过重心法反模糊化,求得u。
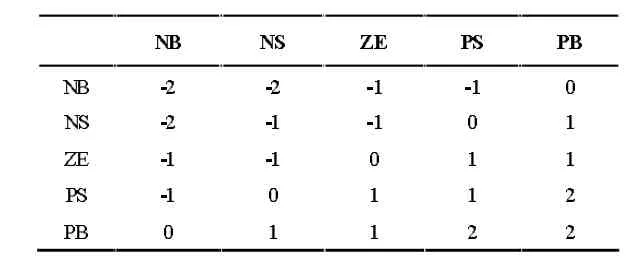
表1 程序模块所采用的模糊规则表
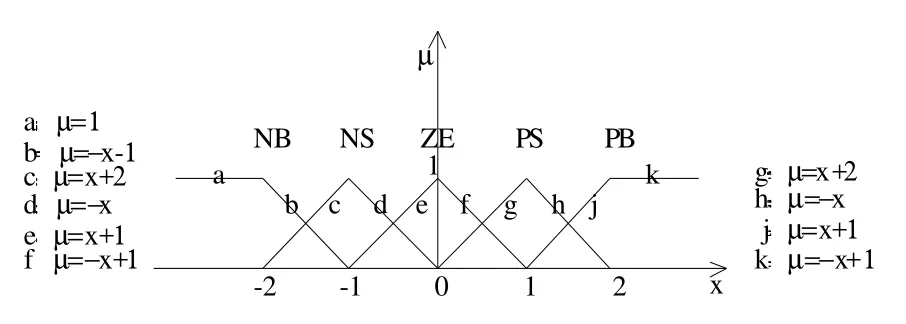
图4 程序模块所采用的隶属函数
3.3 试验内容
3.3.1 试验相关参数选定
1)确定450m3/h新风量对应的新风阀开度为36%(100%对应阀门全开),新风阀前后的静压差为115Pa,试验中保持新风阀开度不变,采用PI控制调节回风阀开度,维持静压差恒定,整定后P值为-200,I值为16。
2)试验中调节电动连续调节阀的开度,改变进入加热盘管的水量,维持送风温度26℃不变,当送风温度大于26℃时,关小水阀开度,当送风温度小于26℃时,开大水阀开度,试验中PI控制的P值为100,I值为16。
3)本试验中静压设定值Pset的初值设为170Pa,为了维持系统的稳定,结合送风量的变化要求以及传感器的量程静压设定值的下限值为80Pa,上限值为240Pa,目标阀位域为[75%,95%],δD=10%,δRST=85%,QD=50m3/h,程序中相关参数的论域是eQ∈[25,150],ecQ∈[-100,100],eP∈[-42%,-10%],ecP∈[-10%,-10%],△PIn∈[10,30],△PDe∈[-30,-10]。
3.3.2 对比试验设计
为了比较参考M模型的静压设定值自适应重置方法(以下简称M模型重置法)和变定静压设定值的方法,其中变定静压设定值法的变化步长取为10Pa,设计一组室内温度设定值变化的试验。假定室内温度值为19℃恒定,按照一定顺序每10min改变一个末端对应的室内温度设定值为20℃或18℃,来体现不室内不同区域负荷变化的差异性,室内温度设定值改变规则如表2。
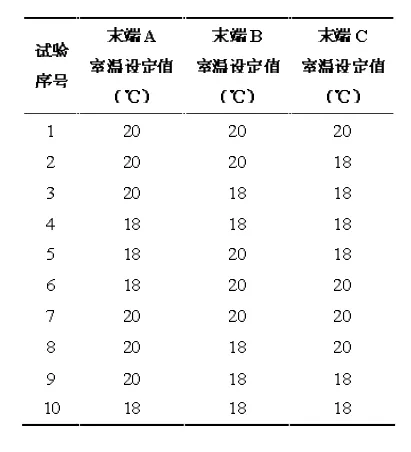
表2 不同末端BOX室内温度设定值表
3.3.3 参考M模型的静压设定值自适应重置方法随实际室内负荷变化试验
试验前将试验房间的门窗敞开2h,使室内温度降低到与室外温度相近水平,然后关闭门窗。试验从早8:00开始进行2h,初始时给定3个末端的温度设定值,空调系统运行近1h改变一次各个末端的温度设定值(表3)。
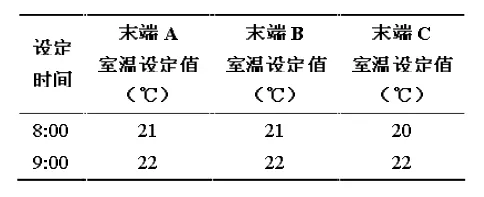
表3 各末端室内设定值
3.4 试验结果
如图5所示,两种不同静压设定值重置方法的静压设定值变化情况。图5中可以看出在控制目标相同的情况下,M模型重置法的静压设定值改变次数为19次,平均值为137.2Pa,阶跃变化绝对值平均量(每两次采样值的差的绝对值之和/采样值改变次数)为1.66Pa/次,变定静压设定值法静压设定值改变次数为45次,平均值为151.2Pa,阶跃变化绝对值平均量为2.35Pa/次。M模型重置法的静压设定值更小,送风机的能耗就会更低,同时阶跃变化绝对值平均量也小,表示该控制方法的稳定性更好。

图5 M模型重置法和变定静压法的静压设定值变化情况
图6表示试验中风机消耗电功率情况,其中时间是按电功率值由小到大的采样时间次序排列。试验中在大部分采样时间内M模型重置法的功率值均小于变定静压法的功率值,且这部分时间均为系统处于部分负荷状态。M模型重置法电功率的平均值为0.338kW,总能耗为0.555kWh,变定静压法的电功率平均值为0.343kW,总能耗为0.562kWh。图7表示,M模型重置法和变定静压法的末端最大阀位和最小阀位情况。

图6 M模型重置法和变定静压法的风机消耗电功率情况
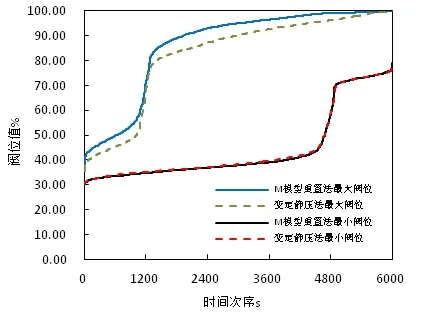
图7 M模型重置法和变定静压法的末端最大和最小阀位情况
图7中M模型重置法的最大阀位平均值为86.11%,最小阀位平均值为44.50%,变定静压法的最大阀位平均值为82.31%,最小阀位的平均值为44.78%,综上M模型重置法在末端阀门上的阻力损失小于变定静压法。图8为M模型重置法随实际负荷变化试验静压设定值和功率值变化情况。
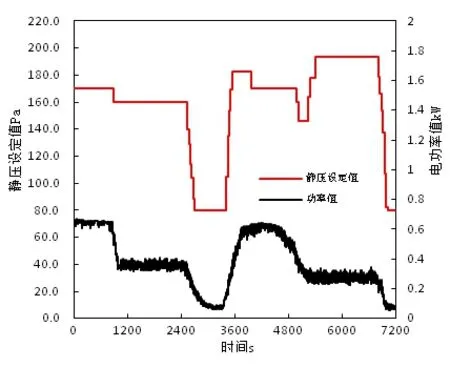
图8 M模型重置法随实际负荷变化试验静压设定值和电功率值变化情况
图8表示了室内温度首先达到初始设定温度和运行1小时后改变温度设定值的静压设定值和功率值变化情况。初始时由于负荷最大,静压设定值维持初始值170Pa,随着室内负荷减少,静压设定值降低到下限值80Pa,此时各个末端达到初始室温设定值,第二次改变室内温度设定值之后,静压设定值开始增加,当再次达到室温设定值时,静压设定值又维持在80Pa的稳定状态。试验过程中静压设定值的平均值为158.5Pa,阶跃变化绝对值平均量为1.62Pa/次,风机消耗电功率的平均值为0.374kW,能耗为0.749kWh。
4 结论
1)最不利热力末端是变风量空调系统中应该避免出现的不利工况,其定义对静压设定值进行合理的重置有重要的意义。
2)最大阀位末端是预先判定最不利热力末端可能出现位置的重要参考依据,本文提出了基于最大阀位末端目标阀位域的Mamdani模糊参考模型的方法进行静压设定值的重置,在避免了最不利热力末端出现的同时获得理想的节能效果。
3)Mamdani模糊参考模型的静压设定值自适应重置方法与变定静压法相比,可以避免其变化步长,静压监测点和静压设定初始值选取困难的问题,使静压设定值的重置有明确目的性和良好的适应性,调整更为迅速,控制系统更加稳定。实际工程中只要确定静压监测点,然后通过对论域进行合理的调整,便能实现静压设定值进行自适应重置。
[1]叶大法,杨国荣.变风量空调系统设计[M].北京:中国建筑工业出版社,2007
[2]杨国荣.变风量空调系统控制[J].暖通空调,2012,42(11):15-19
[3]E H Mamdani.Application of fuzzy algorithm for simple dynamic plant[J].Proc.IEEE.,1974,121(12):1585-1588
[4]欧进萍,张吉礼.作用模糊子集推理方法的研究与应用[J].模糊系统与数学,2000,14(3):58-65
[5]赵天怡.空调冷冻水变压差设定值优化控制方法[D].哈尔滨:哈尔滨工业大学,2010
[6]袁自远.变风量空调系统新风量控制方法试验研究[D].大连:大连理工大学,2013
Study on Sta tic Pre s s ure Ada ptive Re s e t Me thod of VAV Sys te m
DAI Wu-he,ZHANG Ji-li*,ZHAO Tian-yi
Institute of Building Energy,Dalian University of Technology
Two concepts including most unfavorable thermodynamic VAV terminal and maximum valve VAV terminal related to VAV system were introduce,and static pressure value adaptive reset method of Mamdani fuzzy reference model based on target domain of valve position of maximum valve VAV terminal was studied.Variable static pressure automatic control to the supply fan on the air conditioning system intelligent control comprehensive performance test platform of DLUT was accomplished,and the test results show that this method provides greater purpose,quick adjustment to the target domain,small resistance loss to VAV terminal and obvious energy saving effect compared with previous variable static pressure value method.
most unfavorable thermodynamic VAV terminal,maximum valve VAV terminal,target domain of valve position,Mamdani fuzzy reference model,static pressure value,adaptive reset method
1003-0344(2015)05-013-6
2014-3-24
张吉礼(1969~),男,博士,教授;大连市甘井子区凌工路2号大连理工大学建设工程学部3号实验楼417房间(116024);0411-84707735;E-mail:zjldlut@dlut.edu.cn
国家自然科学基金资助项目(No.51078053);国家自然科学基金面上项目(No.51378005)
