阈值改进整数小波与LZW算法相结合的水声数据压缩方法

卓颉，张怡，刘雄厚，刘宗伟



阈值改进整数小波与LZW算法相结合的水声数据压缩方法

卓颉，张怡，刘雄厚，刘宗伟

(西北工业大学声学工程研究所，陕西西安 710072)

提出一种阈值改进整数小波与基于字典编码的LZW（Lempel-Ziv-Welch）算法相结合的数据压缩方法，该方法旨在减少水声数据传输量的同时尽可能地达到高保真。数据压缩过程中，先对水声数据进行整数小波变换，再对变换后的高频系数采用改进的小波阈值算法和阈值函数进行处理，提高了数据压缩倍数和信噪比，降低了误差。最后通过LZW将处理后的系数进行编码输出，进一步提升压缩效果。文中给出了相应的数据压缩算法流程。实际舰船辐射噪声数据的压缩处理结果表明，该方法能有效提高信号信噪比、减少信号失真并能获得更大的压缩倍数。

信号压缩；整数小波变换；LZW算法；阈值；阈值函数

0 引言

随着水下探测技术的快速发展，水声数据的高速远距离传输成为该领域研究的热点之一。传统水声通信因水下信道的复杂性和海洋噪声干扰的影响，无法进行高速率传输。短波和射频通信方式受通信带宽和传播途径的限制，无法进行大量数据传输。无线网桥、有限带宽等传输方式受天线和发射功率的限制，只能在近距离内进行传输。而微波通信方式可同时兼顾远距离和高速率的特点。蒸发波导是一种可用来提供微波宽带超视距传输的无线信道资源，目前已引起了国内外的高度重视，并被应用于水声数据超视距传输[1]。对待传输水声数据进行有效压缩不仅可以节省信息的存储空间，还可大幅提高信息的传输效率。

数据压缩技术广泛应用于信号处理领域，按压缩的可逆性一般分为有损压缩和无损压缩两种[2]。无损压缩能实现信号的精确重构，但其压缩倍数不高。有损压缩则不能实现信号的精确重构，但压缩倍数大大提升。水声数据通常是多阵元的采样数据，具有宽频带、低信噪比、携带信息量大等特点，通常多采用单一的有损数据压缩方法。基于K-L(Karhunen-Loeve)变换的有损压缩方法虽实现简单，运算量较小，但针对实际的水声信号并不能实现精确重构[3]。离散小波变换(Discrete Wavelet Transform, DWT)的压缩方法针对语音信号的压缩效果较好，但无法准确确定最佳小波基的选取[4]。

传统的有损压缩方法并不能实现信号的精确重构，且抗噪声性能差，不利于远距离传输。而基于小波变换的压缩算法在处理非平稳信号、数据压缩方面具有优越性，具有高的压缩倍数、在传递中抗干扰性强等特点，因而得到了广泛的应用[5]。LZW(Lempel-Ziv-Welch)是一种基于字典编码的压缩方法，是当今最具代表性的无损压缩技术[6]，特别适于对大量重复字符或字符串进行编码。它在数据压缩过程中动态地生成一个串表，比较之后的数据同串表中的数据相匹配，匹配成功则输出串表的索引。由于串表索引所用的比特数远小于串的比特数，从而实现数据压缩。文献[7]采用小波变换与Huffman编码的压缩算法，有效提高了数据压缩倍数，但Huffman编码遍历所需的时间较长，不利于数据的实时传输。文献[8]采用小波变换结合LZW的压缩方式，实现了地震数据的无损压缩。不过由于受无损压缩的限制，其压缩倍数有限。

本文以无线信道中的水声数据传输为应用背景，提出了一种阈值改进的整数小波与LZW相结合的数据压缩方法，最终实现水声信号在蒸发波导中的超视距高速率传输。该方法是在LZW算法中引入整数小波变换，实现整数到整数的转换，以方便对处理后的系数进行LZW再压缩，提高压缩效果。由于小波压缩中，阈值及阈值函数的确定起着至关重要的作用[9-11]。所以，本文对变换过程中的小波阈值及阈值函数提出了改进方法，进一步提升了数据的压缩性能。对实测舰船噪声数据处理结果表明，基于阈值改进整数小波与LZW算法相结合的水声数据压缩方法比单一算法的压缩性能明显提升。较传统的小波阈值方法而言，本文提出的阈值改进方法具有更好的压缩效果和保真度及更少的能量损失等优点。该方法不仅适用于水声信号，也可对其它数据进行压缩处理。

1 算法基本原理

1.1 整数小波变换

整数小波变换能实现整数到整数的变换。其实质就是将信号通过一系列的低通和高通滤波器，分别得到近似信号和细节信号。图1给出整数小波分解和重构的流程图。整数小波分解过程一般可分为：分裂、预测和更新三个步骤。

(2)

(3) 更新：为保持原始数据集的整体特性，如均值、能量等，需找出一个更好的子数据集来替换原先的。其中为更新算子，更新后的为低频系数。更新过程如下：

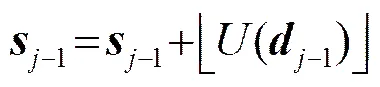
小波重构，就是小波变换的逆过程。过程如下：

(4)

1.2 LZW算法

LZW属字典编码，是利用数据本身包含的重复性而实现压缩的。具体实现步骤如下[3]：

LZW编码算法：

(1) 初始化字典，清空前缀；

(2) 读入下一字符作为当前字符，形成词条<,>；

(3) 判断词条<,>是否在字典中；

①若存在，将词条<,>的编号赋给；

② 若不存在，将词条<,>加入字典中，令=，输出；

(4) 判断串表是否已满或已完成编码；

①若满或完成编码，则清空字典，循环步骤(1)~(4)。

② 否则，置结束码。

LZW译码就是编码的逆运算。解压缩执行时，循环读入编码，将字符串表中与编码对应的字符串输出，同时向表中添加一项。

2 改进的阈值算法及阈值函数

在小波压缩中，分为小波基的选取、阈值确定、选取阈值函数和小波重构四步骤。其中，阈值的确定起着至关重要的作用。整个过程中，因为阈值和阈值函数不是唯一的，阈值确定和阈值函数选取的灵活性很大，这也是小波压缩的核心步骤，所以如何选取阈值和阈值函数起着至关重要的作用。

2.1 已有的阈值算法

(1) 通用阈值算法

文献[9]在Donoho通用阈值的基础上提出了改进方法，阈值的公式为

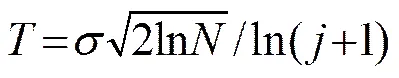
其中：为数据长度；为噪声标准偏差，用第层小波系数中间幅值的绝对值估计，即；为当前的分解层数。局部阈值虽然克服了全局阈值对小波系数“过扼杀”或者“过保留”的倾向，但经该阈值处理后的信号还是往往过于平滑，容易丢失原始信号信息。

(2) 修正NeighShrink阈值算法

NeighShrink法在对系数进行处理时，虽然考虑了其周围系数的分布并将其引入收缩策略。但是，在进行系数收缩时对所有的子带均采用通用全局阈值，而全局阈值存在着一定缺陷——要么信息损失过多，要么噪声残留较多。文献[10]在原有的NeighShrink阈值上提出了改进，阈值的公式为

修正的NeighShrink阈值在压缩效果上有了一定改进，但是对噪声的适应性依然较差。所以，不适合作为阈值来处理低信噪比的水声信号。

(3) Brige-Massart策略阈值

文献[11]中提出的Brige-Massart策略阈值，将每级变换后的系数按绝对值从大到小的顺序排列，按公式(7)选取第个系数作为第层的阈值。阈值的公式为

其中：为分解层数，这里取4；一般指最高层低频系数的长度；为经验值。

Brige-Massart策略阈值虽能自适应地对信号进行处理，但一般不能有效地降低原始信号的噪声。所以，也不适合作为水声信号压缩的阈值。

2.2 改进的阈值算法

改进的阈值算法是在上述三种方法的基础上提出的。假设噪声为高斯白噪声。由于白噪声的Lipschitz指数小于零，而信号却是相反的，即噪声的小波变换模值随分解尺度的增大而快速减小，信号的小波变换模值随分解尺度的增大明显增大[9]。可以认为较小的小波系数由噪声产生，而较大的小波系数由信号产生。通过在各层设定阈值，将小于阈值的小波系数归零，并由剩余的小波系数重构信号。所以，本文提出的改进算法采用局部阈值处理。具体方法为：在较低尺度上选取较大阈值，有效地滤除噪声；在较高尺度上选取较小阈值，尽可能多地保留信号。改进的阈值为

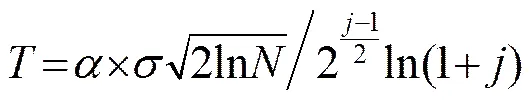
2.3 基于改进阈值函数的小波系数

目前，软阈值函数和硬阈值函数为常用的两种阈值函数。硬阈值函数是将绝对值大于阈值的系数予以保留，其余的系数变为零。它是不连续的，会在某些点产生振荡。软阈值函数在处理绝对值大于阈值的系数时不是完全保留而是作收缩处理，它克服了硬阈值函数的缺点，能在阈值点处连续，处理的结果会光滑、无尖峰，但因为在函数中小波系数减去了一个常数，从而使得处理后的小波系数与原小波系数存在恒定的偏差，影响重构信号与原信号的逼近程度。为了克服软、硬阈值函数的缺点，本文基于2.2节中提出的改进阈值函数定义了新的小波系数，使其既能具有软阈值函数一样的连续性，又保证了重构信号与原始信号的逼近度。定义改进阈值函数与小波系数间的关系式如下：

图2 三种阈值函数曲线图

Fig.2 The functions of three thresholds

3 本文算法流程

采用整数小波变换与LZW算法相结合的水声数据压缩算法的流程如图3所示，具体步骤如下：

(1) 将信号进行整数小波分解，得到对应的低频系数与高频系数；

(2) 利用新阈值公式(8)，计算各层相应的阈值；

(3) 通过改进阈值函数，对高频系数进行处理；

(4) 将低频系数与处理后的高频系数经LZW编码压缩，并传输出去；

(5) 通过解压得到相应的高频系数与低频系数，将这些系数通过小波逆变换，重构出信号。

4 数据处理与分析

4.1 压缩效果的评价标准

本文采用压缩率、信噪比和均方根误差三个指标来衡量压缩效果[12]。三个指标的定义如下：

(2) 信噪比(SNR)：原始信号与重构误差间的比值，主要用于衡量原始信号与重构信号的相似度及能量损失。

(11)

(3) 均方根误差(RMSE)：原始信号与重构信号之间的偏差，是衡量信号保真度的评价标准之一。

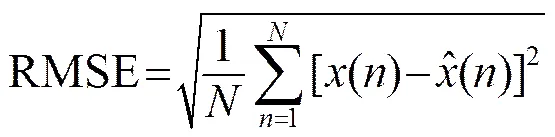
4.2 实验数据分析

为了验证本文方法在水声数据压缩方面的有效性，选取文献[13]中公布的由声呐基阵记录的美国二战期间所用潜艇的辐射噪声作为原始待压缩数据，采样率为22 kHz，取数据长度(即采样点个数)=60000，小波分解为4层，阈值函数中经验值取为0.46。

图4为采用5种不同小波基进行数据压缩的结果对比。式(11)、(12)给出SNR和RMSE是衡量重构信号保真度的主要评价标准。由图4可以看出，虽然采用db4小波基时RMSE最低，但是相比其他的小波基而言，它的压缩倍数较小。此外，它的压缩倍数与SNR的关系趋势并不十分稳定。从图4(a)中还可看出，在压缩倍数达到最大的同时，db6小波基获取的信噪比较高，RMSE较低，更好地保真了原始数据。结合压缩倍数、SNR以及RMSE三种指标，采用db6小波基的压缩效果最好。

图5分别从SNR、RMSE两个方面对不同阈值算法的压缩性能分析比较。图中的B-M策略阈值表示Brige-Massart策略阈值，修正的N-S阈值表示修正NeighShrink阈值法。从图5可以明显看出，相比其他阈值，本文提出的新阈值算法在获得最大压缩倍数的同时，可获得最大信噪比和最小均方误差。此外，与其它阈值算法相比，新阈值算法的压缩倍数与SNR及RMSE间的关系趋势也最稳定。所以，采用新阈值算法的压缩效果最佳。

图6和图7比较了原始信号和重构信号的时域波形与频谱。对比图6中的原始信号与重构信号的时域波形图，可以看出新阈值算法能较好地重构出原始信号波形；而在图7的频谱图中，可以看出新阈值算法对低频线谱成分的保真度较高，有利于后处理中利用线谱成分进行水下目标探测与识别。综合这两幅图，可以得出：本文提出的阈值算法，不仅能使压缩倍数得以提高，还能使数据的保真度得以提升。新阈值算法压缩效果优于现有阈值算法。

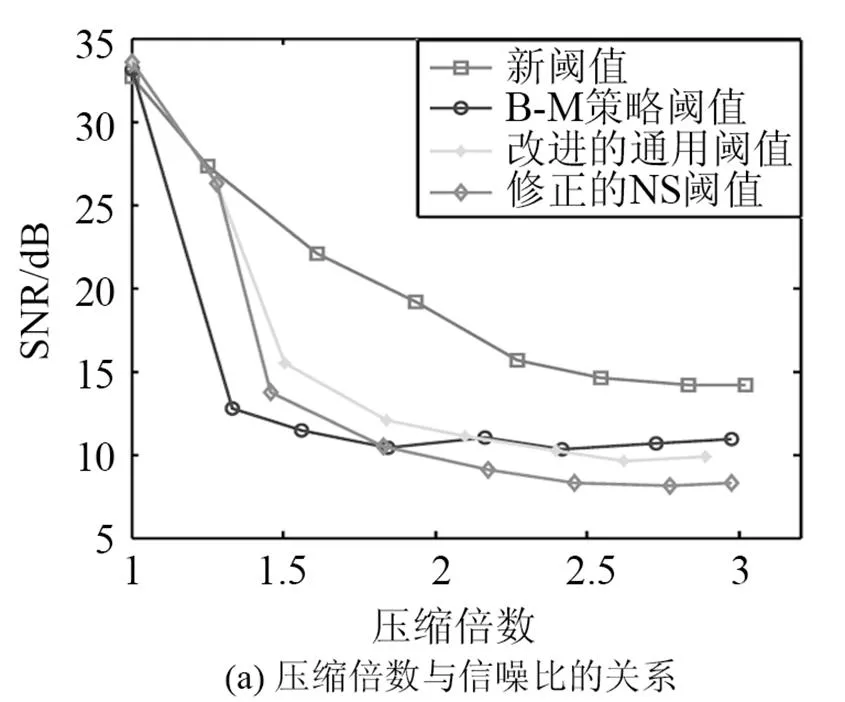
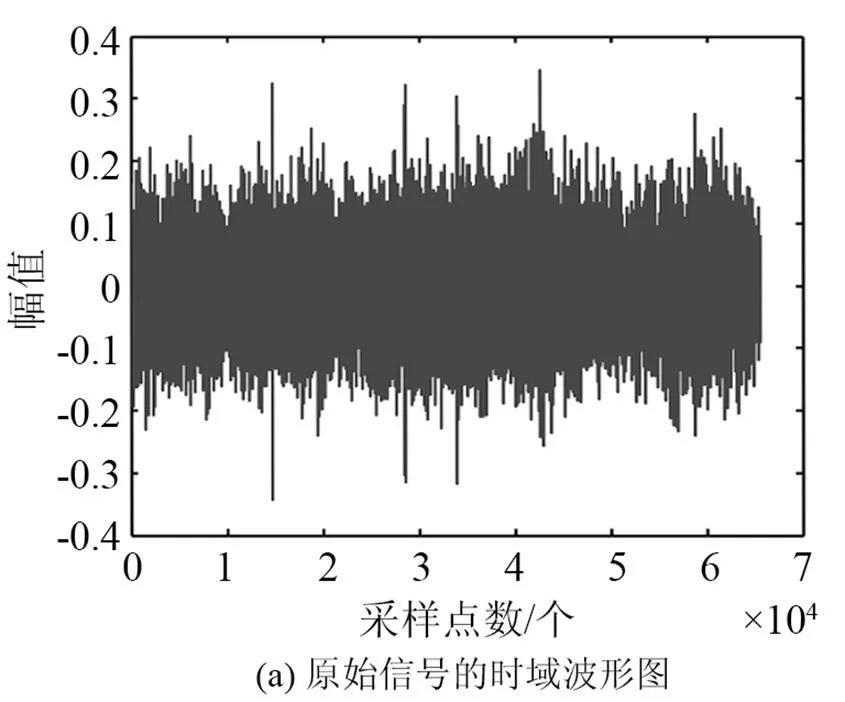
表1利用CR、SNR、RMSE和相关系数四个参数来衡量阈值函数选取的有效性。对比表1中性能参数，可以看出，如果对数据只采用LZW压缩，数据几乎没有被压缩。而在LZW中引入小波变换后，通过选取一定的阈值去掉不重要的系数，保留重要的系数，带来了比较明显的数据压缩效果。此外，分析各性能参数可得出，数据经硬阈值函数处理后RMSE较大，经软阈值函数处理后得到的信噪比较低。而本文提出的新阈值函数同时克服了软、硬阈值函数的缺点，使处理后的数据在获得高信噪比的同时，均方根误差较小，相关系数更高。

表1 几种方法的压缩效果对比

综上所述，采用本文提出的基于阈值改进的整数小波与LZW相结合的压缩方法对水声数据进行处理，可以获得更大的压缩倍数、更高的信噪比以及更低的均方根误差，能更好地保真原始信号。

5 结论

本文提出了一种阈值改进的整数小波与LZW相结合的数据压缩算法，可以有效地对水声数据进行压缩。实测舰船辐射噪声数据的处理结果表明：本文提出的方法比仅采用LZW算法的压缩倍数明显提升；所获得的信噪比、均方根误差、相关系数均远优于以往的阈值算法；在压缩倍数得到提升的同时，能获得更高的保真度和更小的能量损耗。实际舰船噪声处理结果表明该方法的有效性和实用性。由于在数据压缩过程中没有对信号特性进行预设，因此本文方法也适用于其它数据压缩领域。

[1] 张鹏, 杨坤德, 刘艳, 等. 数字微波式远程水声数据采集系统设计[J]. 计算机测量与控制, 2009, 17(7): 1421-1423.

ZHANG Peng, YANG Kunde, LIU Yan, et al. Design of remote underwater acoustic data acquisition system based on digital microwave[J]. Computer Measurement & Control, 2009, 17(7): 1421-1423.

[2] 戴善荣. 数据压缩[M]. 西安: 西安电子科技大学出版社, 2005.

DAI Shanrong. Data compression[M]. Xian: Xian University of Electronic Science and Technology Press, 2005.

[3] 郭晓乐. 水声数据压缩的可行性分析[D]. 西安: 西北工业大学, 2012.

GUO Xiaole. Compression methods to deal with acoustic data[D]. Xian: Northwestern Polytechnical University, 2012.

[4] Jalal Karam, Raed Saad. The effect of different compression schemes on speech signals[J]. World Academy of Science, Engineering and Technology, 2006, 18(1): 87-91.

[5] NING Jiaxin, WANG Jianhui, GAO Wenzhong, et al. A wavelet-based data compression technique for smart grid[J]. IEEE Trans. Smart Grid, 2011, 2(1): 212-218.

[6] 刘晓胜, 王新库, 黄南天, 等. 基于模式相似度和LZW压缩编码的电能质量数据压缩方法[J]. 电力自动化设备, 2012, 32(3): 53-57.

LIU Xiaosheng, WANG Xinku, HUANG Nantian, et al. Power quality data compression based on pattern similarity and LZW compressed encoding[J]. Electric Power Automation Equipment, 2012, 32(3): 53-57.

[7] 张蕊, 王学伟, 王琳. 基于GHM多小波的电力系统故障录波数据压缩算法[J]. 电测与仪表, 2008, 45(10): 46-50.

ZHANG Rui, WANG Xuewei, WANG lin. Compression Algorithm of fault recording data in power system based on GHM multiwavelet[J]. Electrical Measurement & Instrumentation, 2008, 45(10): 46-50.

[8] 刘亮,叶进. 基于小波理论的动平衡信号滤波方法研究[J]. 机械制造与自动化, 2011, 46(1): 51-54.

LIU Liang, YE Jin. Research on method of dynamic balancing signal filtering based on wavelet theory[J]. Machine Building ＆ Automation, 2011, 46(1): 51-54.

[9] Yasser Ghanbari, Mohammad Reza Karami-Mollaei. A new approach for speech enhancement based on the adaptive thresholding of the wavelet packets[J]. Speech Communication, 2006, 48(8): 927-940.

[10] 武海洋, 王慧, 裴宝全. 一种阈值改进的邻域小波系数法图像去噪[J]. 计算机工程与应用, 2011, 47(27): 203-205.

WU Haiyang, WANG Hui, PEI Baoquan. Improved threshold for image de-noising based on NeighShrink[J]. Computer Engineering and Applications, 2011, 47(27): 203-205.

[11] 许同乐, 张新义, 贾庆轩, 等. 基于小波阈值降噪滚动轴承信号的研究[J]. 船舶力学, 2012, 16(10): 1199-1203.

XU Tongle, ZHANG Xinyi, JIA Qingxuan, et al. Rolling bearing fault research on wavelet threshold denoising[J]. Journal of Ship Mechanics, 2012, 16(10): 1199-1203.

[12] 李兰. 基于小波变换的流数据压缩算法研究[D]. 长沙: 湖南大学, 2010.

LI Lan. The research on streaming data compression algorithm based on wavelet transform[D]. Changsha: Hunan University, 2010.

[13] http://www.hnsa.org/sound/#jp.

An underwater acoustic data compression method using improved threshold integer wavelet and LZW algorithm

ZHUO Jie, ZHANG Yi, LIU Xiong-hou, LIU Zong-wei

(Institute of Acoustic Engineering, Northwestern Polytechnical University, Xi’an710072,Shaanxi,China)

A new data compression method is proposed in this paper, which combines the improved threshold integer wavelet with LZW algorithm. Firstly, by using wavelet transform, the sampled underwater acoustic data are decomposed into low- and high-frequency coefficients. Then, after improved threshold processing to high frequency coefficients, the ones above the threshold are remained, thereby reducing the data amount effectively. Finally, the low-frequency coefficients and remained high-frequency ones are coded by LZW coding and transmitted subsequently. The compression algorithm process is given in the paper. By processing the real ship noise data, the new method can effectively improve SNR, reduce signal distortion level and achieve higher compression ratio, compared with the conventional threshold value method.

signal compression; integer wavelet transform; LZW algorithm; threshold value; threshold function

TB688

A

1000-3630(2015)-02-0115-06

10.16300/j.cnki.1000-3630.2015.02.003

2014-01-25;

2014-04-22

国家自然科学基金资助项目(11104222)。

卓颉(1978－), 女, 副教授, 硕士生导师, 研究方向为信号与信息处理。

张怡, E-mail: z_y608@sina.com