The Implementation of DDFS by Using Six Segments QLA Algorithm

LIU Bing，GAO Bo，GONG Min，ZHANG Jie

(Key Laboratory of Micro-Electronics Technology of Sichuan Province，Chengdu 610064，China)

The Implementation of DDFS by Using Six Segments QLA Algorithm

LIU Bing，GAO Bo*，GONG Min，ZHANG Jie

(Key Laboratory of Micro-Electronics Technology of Sichuan Province，Chengdu 610064，China)

In order to improve the performance and the resource utilization of DDFS，researches about symmetry of sine and line approximation method(QLA)have been done．The proposed DDFS design uses six evenly distributed lines whose values are less than sine to approximate the sine value，and QE-ROM to store the different values of sine and six-segments，and the design obtains results less algorithm hardware complexity and less ROM in the condition of the same error．The experiment shows for 9 bits output’s DDFS，this method only uses 336 bit ROM，4 adder 3 multiplexer，and achieves a max frequence of 210 MHz．In FPGA，this method uses 110 LEs，49 registers，which have higher ROM compression ratio．

FPGA;DDFS(Direct Digital Frequency Synthesizer);six segment QLA;phase convert;ROM compression

数字频率合成器是现代电子系统中的重要组成部分，它的作用是产生所需频率的正弦、余弦波形以实现信号的调制和解调。相对于其他合成器，DDFS具有开关速度快，频率分辨率高，相位噪声小，频率切换时相位连续，输出频率非常稳定等特点［1］。DDFS是基于Tierney，Rader和Gold于1971年提出的数字频率合成器的概念［2］，但是该结构的数字频率合成器需要大量的存储器存储幅值，如果采用传统LUT的结构，假设输出是S位，输入是K位，那么就会需要S×2K位的存储空间，如此大的存储器设计，存取时间长，面积大，功耗也很高，不利于集成化设计;如果采用CORDIC算法循环迭代会使延迟增大［3－4］，分段线性插值的办法虽然能达到较高的性能要求，但是使用到了乘法器，加法器和RAM，硬件资源消耗多［5］，为了适应目前高速度，低功耗要求，低延迟，引入线性幅值逼近算法，减小存储器每个数据的位宽，大幅减小存储器的存储量、简化逻辑以达到设计需求［6－8］。在此基础上提出了一种6段的线性分段方法，然后采用QE-ROM的存储方式，成功的降低了系统的复杂度，减少了硬件消耗。

1　分段算法的研究

1．1分段算法原理与分析

频率合成器的结构图如图1所示。

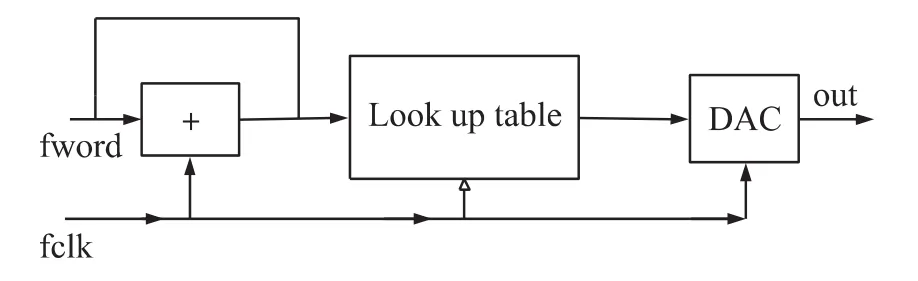
图1　数字频率合成器结构图

由此得到的正弦信号的频率为:

传统的DDFS分段算法是对相位分成2K段，对每一段用一段线段模拟，如文献［9］中利用三角函数的对称性和一次泰勒展式近似，通过两个查找表将相位Φ变换为sin(Φ):

其中a代表每个分段点的相位值。ROM存储b(a)和m(a)，其中b(a)是分段线性函数的起始点，b(a)表达式为:

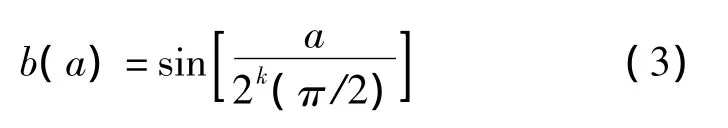
ΔΦ是Φ与小于Φ的最近分段点的相位差:

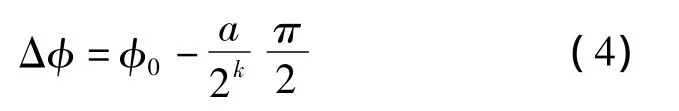
m(a)是两个相邻的分段点之间连线的斜率:

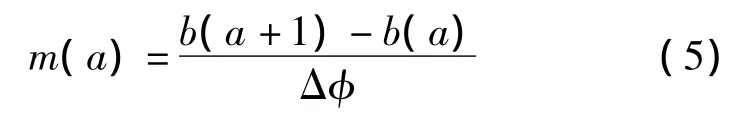
存储器存储b(a)，m(a)的值，压缩比只能达到10．3∶1。

分段线性算法采用各段均分的线段逼近正弦值，然后用ROM存储差值的，以减小ROM存储的位宽［7］。利用三角函数近似:

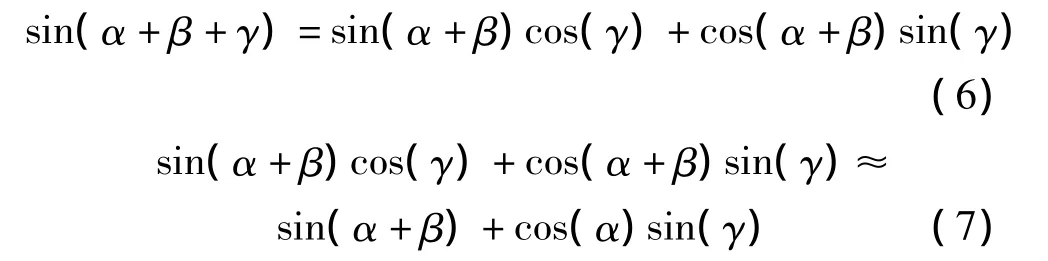
然后分别存储sin(α+β)和cos(α)sin(γ)的值，针对sin(α+β)考虑α+β=θ，存储sin(θ)可以使用四线线性逼近的方法，4条直线是相对于π/4对称的其实现了存储位宽减少4位，压缩比也只能达到50．08［6］;优化以后最终实现了压缩比78．2∶1［9］。使用一阶泰勒展式近似实现，使用了3个存储器，1个乘法器，2个加法器［10］。使用dual-slope近似在文献［9］的基础上进一步减小了存储空间。上述文章中使用线性逼近算法和插值技术实现了高的压缩比，但是他们的方法中硬件结构复杂，控制电路复杂，实现难度相对较大。所以需要提出一个结构简单，实现难度低的分段方法。

1．2分段算法实现

综合考虑硬件实现的复杂性和整体硬件面积，在适当提高压缩比的前提下，少量增加硬件复杂度，并利用三角函数对称性和六线线性逼近的方法，提出如式(8)～式(13)的分段方法。其中在存储器存储的值为sin［(π/2)Φ］－Φ－f(Φ)其中Φ为输入相位，f(Φ)为:

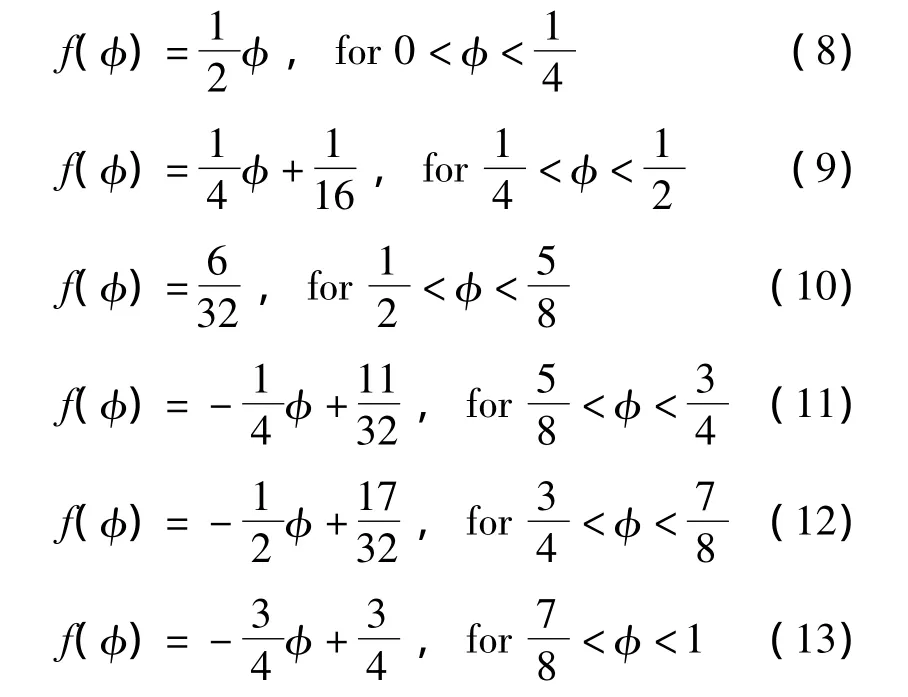
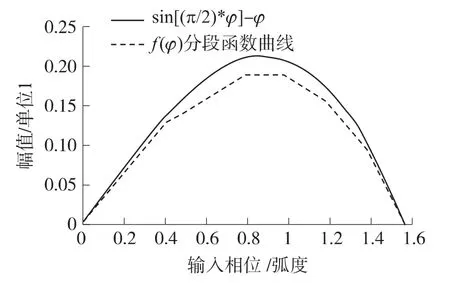
图2　sin((π/2)*Φ)－Φ和六段线性曲线图(幅值单位1，设正弦最大幅值为1)

通过计算可得:

所以对于正弦值每个数据点将节省5位。

误差存储器使用量化和误差存储的方法(QEROM)实现，量化存储器(Q-ROM)利用函数的连续性，将2K个地址均匀分成2L份，每一段有Q-bits量化的值，E-ROM(误差存储)存储被存储的原始值与QROM之间的差值，所以E-ROM中数据的大小将远小于被存储原始值，本文设计过程中实现采用212地址输入9位输出，量化之时将的值乘以210，在第1象限，210个地址输入被分成24段，每个数据5位，数据量化方式如图3所示。

图3中，横轴表示相位值，纵轴为存储量化值的210倍。依据最小误差选取不同量化方法分段设置存储位宽信息，从而保证在误差范围内达到最小存储位宽设计。

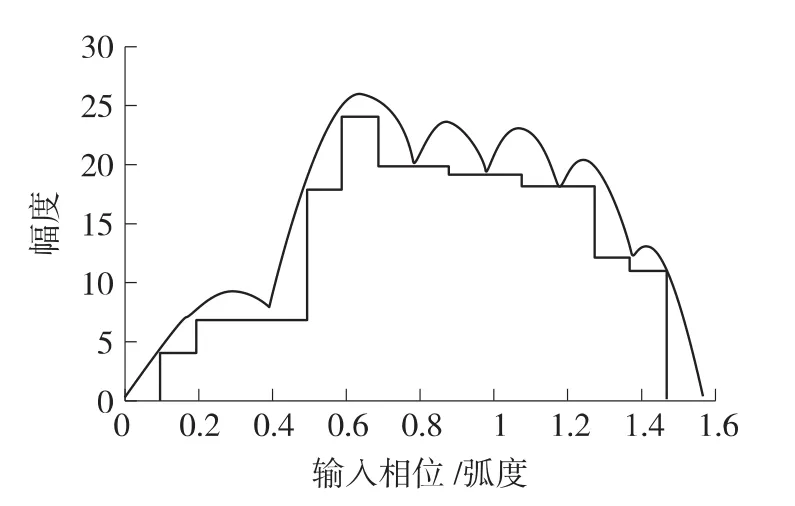
图3　Q-ROM里存储的数据(幅值单位为1，正弦最大幅值为210－1)

在本文的实现中E-ROM只需将210个地址输入被分成26段，每个数据位宽为4 bit，E-ROM的值为小于原始值和Q-ROM存储值之间的差值的最大整数加上2，并在输出之前进行溢出判断。

系统的运算单元将线性分段函数与QE-ROM的存储值相加得到最终的正弦值，余弦值的计算方式可以通过相移得到，系统包括4个加法器，3个多路选择器，和2个存储器，与一个比较器。系统硬件结构图如图4所示。

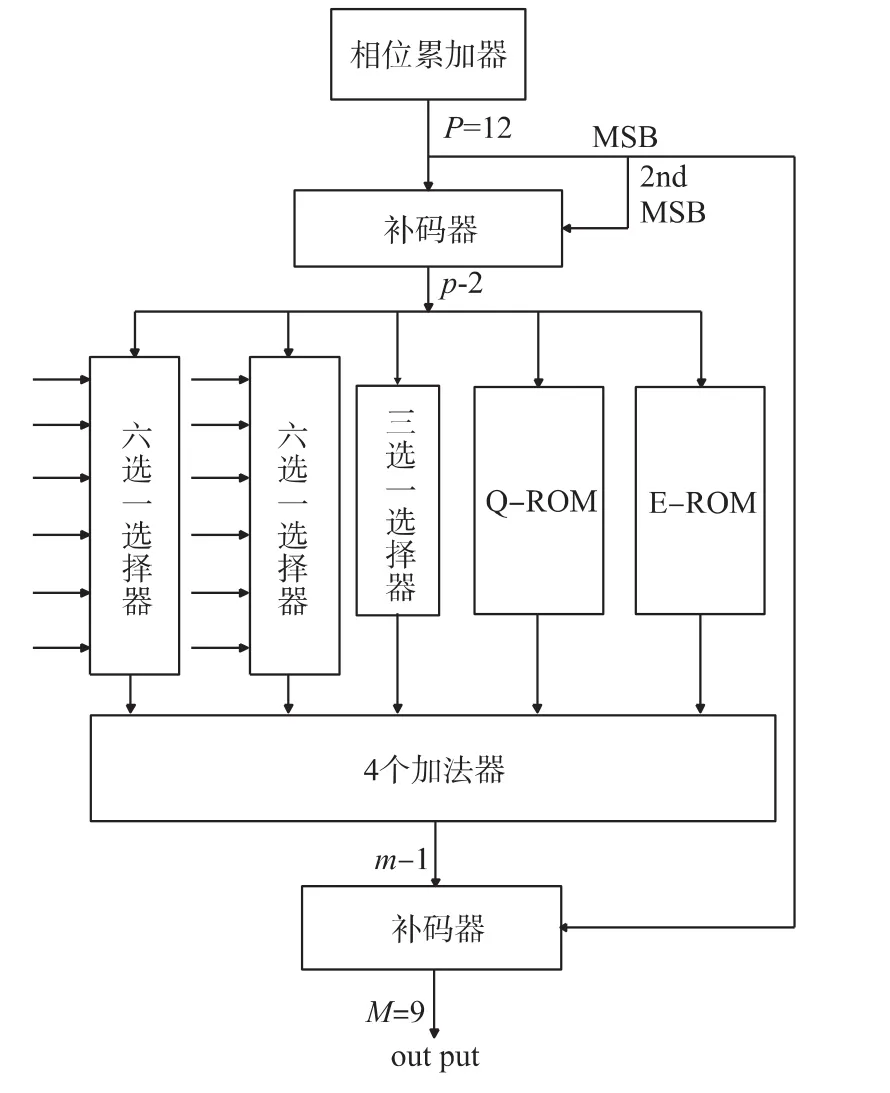
图4　系统结构图

按照六段线性逼近算法原理中描述，安排3个选择器输出线性函数的值，使线性函数的求值过程无需复杂单元而只用加法器就可以实现。

2　系统综合与仿真

系统设计采用Altera的CycloneⅡEP2C5AF256A7芯片实现，Verilog源代码在Altera的Quartus 10．1软件版本中综合实现的，共四分之一个周期的硬件共消耗资源110个LE，49个存储器，最大的工作频率达到了210 MHz;和其他方法的对比如表1所示。

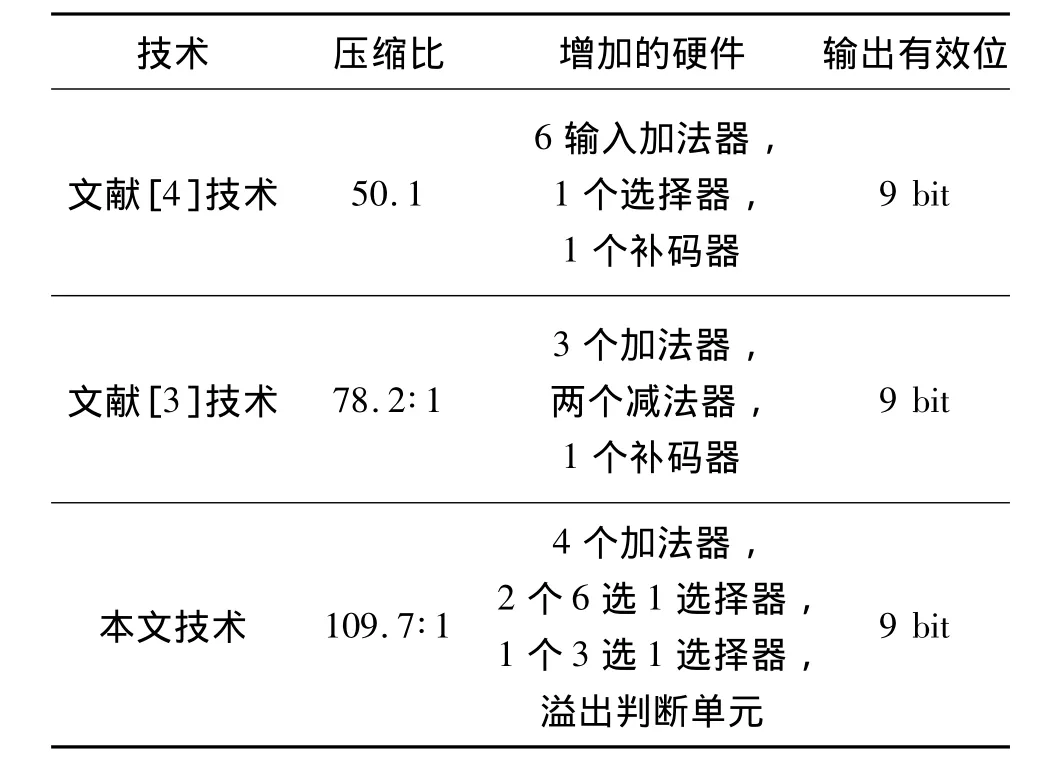
表1　本文的技术与其他技术对比

针对系统误差的仿真编写了相应的测试模块，考虑到三角函数的对称性，只需仿真第1象限的结果，即能反映出整体设计指标，在Modelsim 6．5se中的仿真，当相位累加器的输入为1时的部分波形时序图如图5所示。

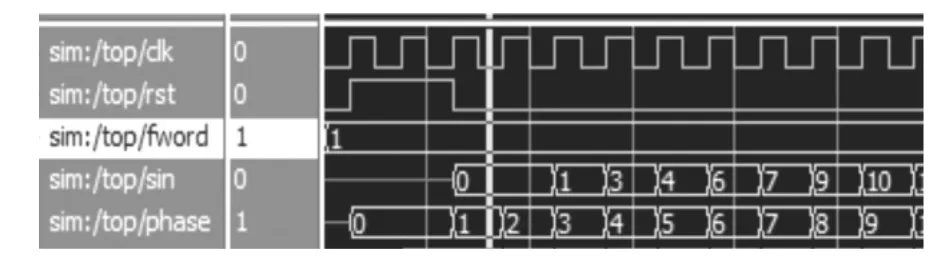
图5　当相位累加器的输入为1时的Modelsim仿真

将Modelsim仿真产生的正弦值(变量名是sin)输出之后导入到MATLAB和MATLAB中正弦函数的精确结果进行对比得到如图6的仿真图。

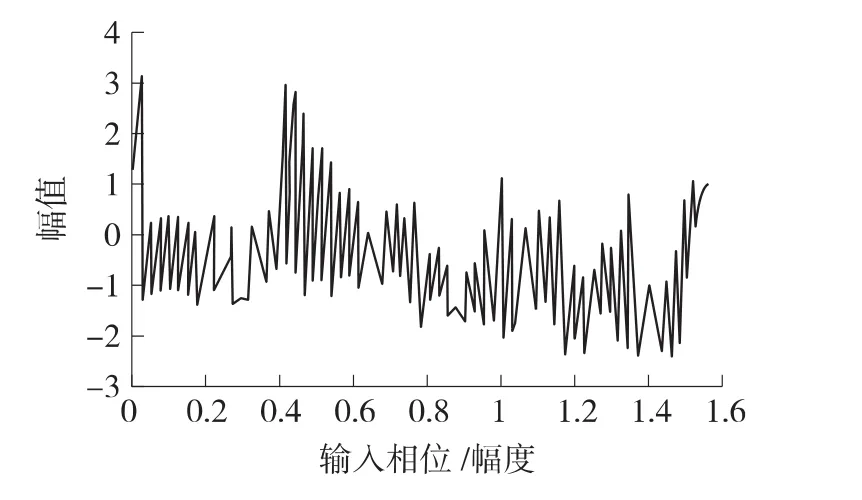
图6　系统误差仿真图:精确的正弦值与HDL算法得到的值之差(幅值单位为1，最大幅值为210－1)

最终误差的最大值为1．565×2－9，按照误差原理和正弦函数的对称性验证了该设计可以达到9位输出有效。

通过系统综合和时序分析过程得到该设计电路最大时钟为210．35 MHz，消耗的硬件资源为110个LE，49个寄存器。使用quartus ii10．1的TimQuest Timing Analyzer分析HDL设计的时序:

表2　时序分析报告结果

3　结束语

文章结合三角函数对称性和六线逼近法，减小存储器的大小，完成了DDFS 9位输出有效，通过改变输入到累加器中的fword值，可以调整该DDFS输出波形的最小频率为51．2 kHz(系统工作时钟为210 MHz)，通过调整QE-ROM存储位宽也可以将输出有效位宽调整为想要的位宽。文章提出的六线逼近算法成功将存储器的存储总量减小，实现高压缩比的DDFS设计，通过逻辑综合和仿真验证获得优于同类算法的硬件资源消耗。总体设计采用1个3选1，2个6选1选择器，4个加法器和2个存储单元，1个比较器实现，其中存储器只需要336 bit。设计算法实现了高压缩比的直接数字频率计的设计，并通过FPGA电路的综合和仿真验证了该设计方案的正确性。

［1］王春林，吴建辉，叶双应，等．一种基于非均匀分段线性插值的直接数字频率合成器［J］．电子器件，2006，29(2):508－511，588．

［2］Tierney J，Rader C M，Gold B．A Digital Frequency Synthesizer［J］．Audio and Electroacoustics，IEEE Transactions on，1971，19:48－57．

［3］Hatai I C I．A Novel Low-Latency，High-Speed DDFS Architecture［C］//India Conference(INDICON)，2010 Annual IEEE，2010: 1－4．

［4］王佳琪，熊先越．基于FPGA的流水线CORDIC算法的DDFS设计［J］．光通信技术，2012(4):61－62．

［5］代向明．线性插值的任意函数发生器及其实现［J］．电子器件，2008，31(4):1397－1400，1404．

［6］Zhao X，Qi J，Tu B H，et al．Design Parallel Direct Digital Frequency Synthesizer Using Interpolation and QLA Technology［C］//Signal Processing，2006 8th International Conference on，vol．1，2006:16－20．

［7］Byung-Do Y，Jang-Hong C，Seon-Ho H．An 800-MHz Low-Power Direct Digital Frequency Synthesizer with an On-Chip D/a Converter［J］．Solid-State Circuits，IEEE Journal of，2004，39:761－774．

［8］Cao X，Ni W，Yuan L．A Compact Direct Digital Frequency Synthesizer for System-On-Chip［C］//Solid-State and Integrated-Circuit Technology，2008．ICSICT 2008．9th International Conference on，2008:1863－1866．

［9］Shiann-Shiun J，Hsing-Chen L，Chen-Yu W．High-Performance DDFS Design Using the Equi-Section Division Method［J］．Ultrasonics，Ferroelectrics and Frequency Control，IEEE Transactions on，2010，57:2616－2626．

［10］De Caro D，Strollo A G M．High-Performance Direct Digital Frequency Synthesizers in 0．25 μm CMOS Using Dual-Slope Approximation［J］．Solid-State Circuits，IEEE Journal of，2005，40:2220－2227．

刘兵(1990－)，男，汉，四川遂宁，硕士研究生，研究方向为超大规模集成电路设计;

龚敏(1961－)，男，四川大学教授，博士生导师，从事新型半导体材料与器件工艺、集成电路设计和工艺及半导体器件的辐照效应研究;

高博(1975－)，男，四川大学副教授，主要从事CMOS集成电路芯片设计和生物医学成像领域的研究;

张杰(1989－)，男，汉族，四川达州，硕士研究生，研究方向为超大规模集成电路。

EEACC:7250E10．3969/j．issn．1005－9490．2015．01．046

基于六线逼近法的DDFS算法的实现

刘兵，高博*，龚敏，张杰
(四川省微电子技术重点实验室，成都610064)

为了提高直接数字频率合成技术的资源利用率，结合三角函数的对称性和线性幅值逼近算法对正弦信号分段算法进行研究，提出基于六线线性逼近优化算法，使用6段不大于正弦值的均与分段的线段逼近之后，使用QE-ROM(量化－误差存储)存储线段与正弦值差值的办法，在不影响频率特征和最大误差特性基础上，实现了算法的简化，并压缩了误差补偿存储器所需存储空间。实验结果表明对于9 bit正弦输出只需使用336 bit存储器和4个加法器3个选择器一个比较器即可实现整个系统，并且最大的工作频率达到了210 MHz，共消耗110个LE，49个存储器。压缩比远远高于传统的压缩算法。

FPGA，直接数字频率合成器;六线线性逼近优化算法;相位转换;存储器压缩

TN402

A文献标识码:1005－9490(2015)01－0218－04

2014－03－26修改日期:2014－04－23