一种求解最优控制问题的变时间节点控制向量参数化方法

李国栋，刘兴高



一种求解最优控制问题的变时间节点控制向量参数化方法

李国栋，刘兴高

（浙江大学控制系，工业控制技术国家重点实验室，浙江杭州 310027）

控制向量参数化方法是求解最优控制问题的一种常用数值方法。它通过离散化控制时域，将控制向量近似地表示成一组参数化的函数。离散化后的时间网格通常是固定的，其划分会影响到最优控制问题数值求解的精度和效率。为了同时优化控制参数和时间网格节点，提出了一种时间节点可变的控制向量参数化方法。推导出了最优控制性能指标对时间参数的导数与对时间分段长度导数之间的关系，得到了性能指标的梯度表达式。用两个经典最优控制实例对所提出的方法进行了测试，结果表明所提出方法能够更好地逼近最优控制轨迹。

过程控制；控制向量参数化；变时间节点；优化；算法

引 言

最优控制问题又称为动态优化问题，在化工领域广泛存在[1-4]。目前，最优控制问题的数值求解算法可分为两大类：间接法[5-6]和直接法[7-8]。间接法通过求解原问题的最优性条件（即必要条件），间接地获得原问题的最优解，而直接法则是通过离散化，将无限维的最优控制问题转化为有限维的非线性规划（nonlinear programming, NLP）问题进行求解。仅离散化控制向量而保持状态向量不变的直接法又称为控制向量参数化（control vector parameterization，CVP）方法，它是当前求解最优控制问题的一种主流数值方法。

在CVP方法中，时间网格的划分通常是事先确定的，并且在优化过程中不会改变。网格的划分直接关系到求解结果对最优控制轨迹的逼近程度。有时为了较好地逼近最优控制轨迹，需要将时间网格划分得很细，但这样会增加NLP问题的维数和计算时间。而且，如果时间网格划分不当还会导致病态的NLP问题，影响收敛速度。针对固定时间网格CVP方法的缺点，国际上许多学者对时间网格的划分和优化展开了研究。

Marquardt等[9-11]提出了自适应网格划分的CVP方法，在迭代过程中通过对上一步解的小波分析来调整时间网格的划分，对某些时间网格进行细化或合并，从而获得比均匀划分网格的CVP方法更高的优化效率。Srinivasan等[12]基于最优控制的必要条件研究了最优控制的各段轨迹与必要条件的对应情况，将必要条件划分为约束和灵敏度两部分，提出了一种具自适应控制向量参数化方法。Szymkat等[13]给出了控制和状态约束最优控制问题的结构估计方法，通过不断增减网格节点和弧段来实现结构调整。这些是属于时间网格精细化调整的方法。另一类方法则是对时间节点的位置进行优化。如Teo等[14-16]提出的一种控制参数化增强转换（control parameterization enhancing transform，CPET）方法，把原时间节点映射到一个新的时间尺度上，并将原有网格的宽度作为优化变量，在求解得到最优控制参数的同时获得最佳的网格划分。该方法有效实现了可变时间节点问题到固定时间节点问题的转换，但这种转换仅具有一种时间网格划分，使得所有的控制变量均基于同一时间网格进行参数化[17]。

对于含有多个控制变量的最优控制问题，各控制分量的最优轨迹往往是不同的，每个控制分量在参数化时应当对应各自的网格划分。本文针对这一情况提出了一种变时间节点控制向量参数化（variable time nodes CVP, VTNCVP）方法，该方法为每个控制分量分配独立的参数化网格，不同于Teo等将时间分段长度作为优化变量，在参数化时直接将时间节点作为优化变量，并且在求解最佳控制参数的同时完成对各控制分量时间网格节点的优化。

1 问题描述

本文考虑的最优控制问题P1的数学描述如下

设是()的可行控制集，则最优控制问题[式(1)～式(7)]可以简单描述为：在可行初始条件[式(5)]下，从可行控制集中求得针对系统[式(2)～式(4)]的最优控制策略，使得目标函数[式(1)]的值最小。

2 理论推导及算法描述

2.1 CVP

图1 分段常量参数化

对问题P1采用分段常量参数化，记第个控制分量的表征参数依次为，并记向量，则在时间段上，可近似地表示为

这样控制向量()的边界约束可以直接转换为控制参数的边界约束。通过分段常量参数化，原始的求解最优控制轨迹的最优控制问题P1就转化为如下所示的确定控制参数的NLP问题P2

2.2 VTNCVP

当最优控制问题中存在多个控制时，各控制分量所适合的网格划分往往是不同的。因此，在进行分段常量参数化时，各控制分量可在不同的时间网格上进行。设第个控制分量的控制时域被时间节点分为了个阶段，其中，为可变时间节点参数。记各控制分量的时间节点参数共有个，并将它们记作向量，则参数化后的控制向量由控制参数和时间节点参数共同确定（图2）。

图2 变时间节点分段常量参数化

因此，问题P1在经过变时间节点控制向量参数化后就转化为求解控制参数和时间节点参数的NLP问题P3

2.3 梯度计算

为了求解参数化后的NLP问题P3，需要获得目标与约束函数对控制参数和时间节点参数的梯度信息。

其伴随方程可表示为

利用Teo等[14-16]给出的CPET方法中目标与约束函数对时间分段长度的梯度计算公式，可推导得到对时间节点参数的梯度。将时间节点参数由小到大进行排序并依次记为，其中时间节点的序号为。通过这些时间节点可将整个控制时域划分成个阶段，记各阶段的区间长度依次为，并令和，那么时间节点和区间长度之间可通过式(24)、式(25)相互表示

其中，函数对时间节点参数的梯度和对时间分段长度的梯度之间的关系，用如下定理来表示。

证明：如式(25)所示，各阶段的区间长度可由时间节点进行表示，因此有

基于定理1和Teo等[14-16]给出的对时间分段长度的梯度公式，可得到函数对时间节点参数的梯度表达式，如定理2所示。

具体的推导过程见文献[14]。将式(31)代入式(26)中，即可得到函数对时间节点的梯度表达式(30)。

2.4 算法描述与分析

基于以上推导，变时间节点控制向量参数化方法的算法实现步骤如下。

②计算微分方程组的初值问题式(2)和式(5)，得到状态()的值。

⑤基于获得的函数和梯度信息解非线性规划问题P3，直至得到优化后的参数和。

与CPET方法相比，所提出的VTNCVP方法具有以下几点优势。

① 时间网格的划分更加自由、灵活。CPET方法中，时间节点被映射并固定在新的时间尺度上，迫使不同的控制分量均在同一时间网格上参数化；而本文所提出的方法，对各个控制分量采用不同的时间网格划分，各分量之间的网格划分不会相互限制和干扰（图3）。

图3 VTNCVP与CPET时间网格对比

②对最优控制轨迹的逼近能力更强。由于VTNCVP方法的时间网格划分更加灵活，各控制分量的参数化表示能够更好地逼近最优控制轨迹，因此，在同等分段数下，VTNCVP方法所得到的最优值优于或等于CPET方法所得到的最优值；在取得相同最优值的条件下，VTNCVP方法所必需的参数数目要少于或等于CPET方法。

③具有更好的收敛能力和数值表现。由于在设置初始参数时，最优控制问题解的结构通常是未知的，因此，在优化计算的过程中，难免会对控制分量间的时间节点顺序进行调整。因为CPET方法将时间节点映射并固定在新的时间尺度上，各节点的顺序是固定的，所以，当节点顺序需要调整时，待调整的节点只能相互靠近而不能交换位置（图4），容易导致求解过程陷入局部最优。而VTNCVP方法则能克服此种缺陷，各控制分量间的节点顺序可以自由调整，从而能够更好地收敛到最优解。

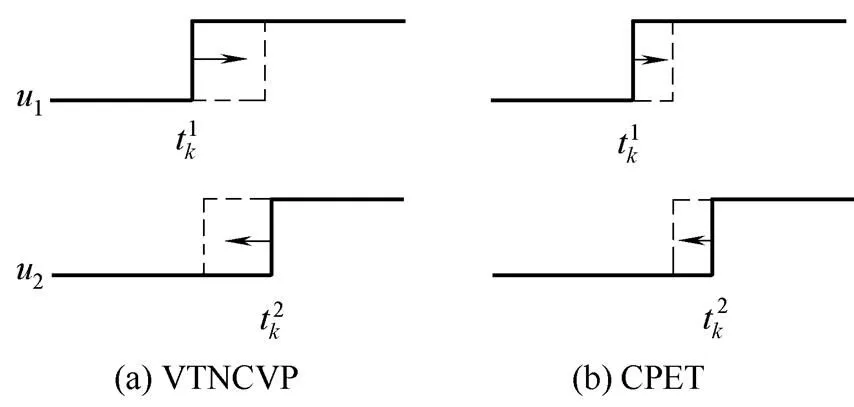
图4 VTNCVP与CPET时间节点优化对比

3 算例测试

3.1 集装箱起重机问题

这是一个经典的复杂机械工程最优控制问题：用起重机将集装箱从货轮转运到卡车上，如何操作使得性能指标最优[19]，含有6个状态变量、2个控制变量、6个微分方程、2个初值/终值等式约束、8个控制变量/状态变量不等式路径约束。该问题的数学模型为

表1 集装箱起重机问题的求解结果

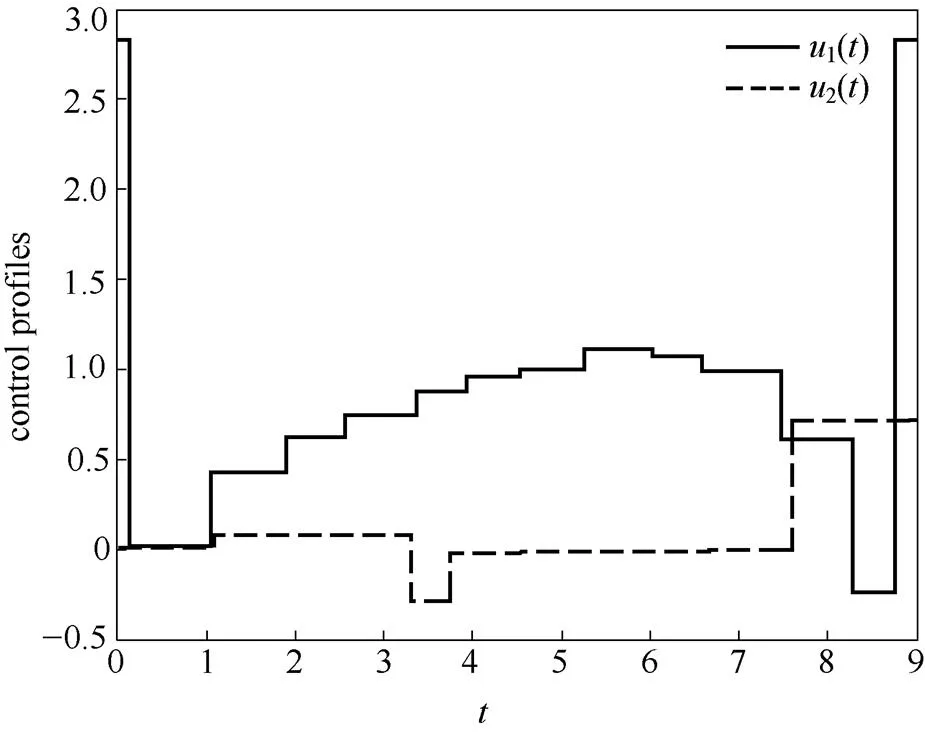
图5 集装箱起重机问题的最优控制轨迹

3.2 复合Nishida问题

这是一个经典的化工过程最优控制问题[21]，其数学模型为

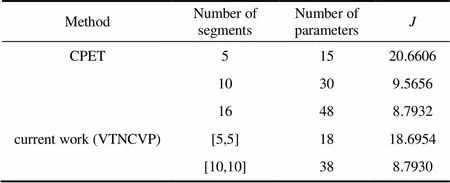
表2 复合Nishida问题求解结果

图6 复合Nishida问题的最优控制轨迹

4 结 论

本文着重考虑控制向量参数化方法求解最优控制问题时，时间网格的划分对非线性规划问题的维数和求解效果的影响。所提出的变时间节点控制向量参数化方法的优点在于可以通过优化时间节点使不同的控制具有不同的网格划分，该方法能够在较少的时间分段下获得更好的结果，比传统方法具有更大的灵活性和更好的控制轨迹逼近效果。

符 号 说 明

Gi，gi——分别为参数化后、参数化前的第i个目标或约束函数 Hi——第i个目标或约束函数的哈密尔顿函数 J——性能指标 Li——第i个目标或约束函数的积分项 N，Nj——分别为控制向量的分段数、第j个控制分量的分段数 nu，nx——分别为控制向量、状态向量的维数 p——时间节点参数数目 t——时间节点参数向量 U——可行控制集 u，，，——分别为控制向量，最优控制向量，控制向量上界、下界 x，x0——分别为状态向量及其初值 ——控制参数向量 ——伴随状态向量 ——排序后的时间节点参数向量 下角标 f——终端 i——目标或约束函数的序号 j——控制分量的序号 k——时间分段的序号 0——起始

References

[1] Zhou You (周游), Zhao Chengye (赵成业), Liu Xinggao (刘兴高). An iteratively adaptive particle swarm optimization approach for solving chemical dynamic optimization problems [J].(化工学报), 2014, 65 (4): 1296-1302

[2] Peng Xin (彭鑫), Qi Rongbin (祁荣宾), Du Wenli (杜文莉), Qian Feng (钱锋). An improved knowledge evolution algorithm and its application to chemical process dynamic optimization [J].(化工学报), 2012, 63 (3): 841-850

[3] Zhou Y, Liu X. Control parameterization-based adaptive particle swarm approach for solving chemical dynamic optimization problems [J]., 2014, 37 (4): 692-702

[4] Liu X, Chen L, Hu Y. Solution of chemical dynamic optimization using the simultaneous strategies [J]., 2013, 21 (1): 55-63

[5] Kirk D E. Optimal Control Theory: An Introduction[M]. New York: Dover Publications, 2004

[6] Peng Haijun (彭海军), Gao Qiang (高强), Wu Zhigang (吴志刚), Zhong Wanxie (钟万勰). A mixed variable variational method for optimal control problems with applications in aerospace control [J].(自动化学报), 2011, 37 (10): 1248-1255

[7] Qi Rongbin (祁荣宾), Liu Chenxia (刘趁霞), Zhong Weimin (钟伟民), Qian Feng (钱锋). A multi-objective optimization algorithm based on gradient information [J].(化工学报), 2013, 64 (12): 4401-4409

[8] Sun Yong (孙勇), Zhang Maorui (张卯瑞), Liang Xiaoling (梁晓玲). Improved Gauss pseudospectral method for solving nonlinear optimal control problem with complex constraints [J].(自动化学报), 2013, 39 (5): 672-678

[9] Binder T, Cruse A, Cruz Villar C A, Marquardt W. Dynamic optimization using a wavelet based adaptive control vector parameterization strategy [J]., 2000, 24 (2-7): 1201-1207

[10] Schlegel M, Stockmann K, Binder T, Marquardt W. Dynamic optimization using adaptive control vector parameterization [J]., 2005, 29 (8): 1731-1751

[11] Assassa F, Marquardt W. Dynamic optimization using adaptive direct multiple shooting [J]., 2014, 60: 242-259

[12] Srinivasan B, Palanki S, Bonvin D. Dynamic optimization of batch processes (Ⅰ): Characterization of the nominal solution [J]., 2003, 27 (1): 1-26

[13] Szymkat M, Korytowski A. Method of monotone structural evolution for control and state constrained optimal control problems//Proceedings of the European Control Conference [C]. University of Cambridge, UK, 2003

[14] Teo K L, Jennings L S, Lee H W J, Rehbock V. The control parameterization enhancing transform for constrained optimal control problems [J].,,, 1999, 40 (3): 314-335

[15] Loxton R C, Teo K L, Rehbock V. Optimal control problems with multiple characteristic time points in the objective and constraints [J]., 2008, 44 (11): 2923-2929

[16] Loxton R C, Teo K L, Rehbock V, Yiu K F C. Optimal control problems with a continuous inequality constraint on the state and the control [J]., 2009, 45 (10): 2250-2257

[17] Zhang Xiaodong (张晓东), Li Shurong (李树荣), Lei Yang (雷阳), Zhang Qiang (张强). Control vector parameterization approach with variable time nodes [J].(化工学报), 2012, 63 (9): 2805-2811

[18] Biegler L T. Nonlinear Programming: Concepts, Algorithms, and Applications to Chemical Processes[M]. Philadelphia: Society for Industrial & Applied Mathematics,U.S., 2010

[19] Sakawa Y, Shindo Y. Optimal control of container cranes [J]., 1982, 18 (3): 257-266

[20] Hu Yunqing (胡云卿), Liu Xinggao (刘兴高), Xue Anke (薛安克). A penalty method for solving inequality path constrained optimal control problems [J].(自动化学报), 2013, 39 (12): 1996-2001

[21] Nishida N, Liu Y, Lapidus L, Hiratsuka S. An effective computational algorithm for suboptimal singular and/or bang-bang control (Ⅱ): Applications to nonlinear lumped and distributed systems [J]., 1976, 22 (3): 513-523

A variable time nodes control vector parameterization approach for solving optimal control problems

LI Guodong, LIU Xinggao

(State Key Laboratory of Industry Control Technology, Department of Control, Zhejiang University, Hangzhou 310027, Zhejiang, China)

Control vector parameterization (CVP) is a frequently used numerical method for solving optimal control problems, where the control vector is approximated by a group of parametric functions through time discretization. Usually, the discretized time grid is fixed, and its partition will affect accuracy and performance of the numerical solution of optimal control problem. To optimize both the control parameters and the time grid nodes, a CVP method with variable time nodes was proposed. Based on the derived relationship between the gradients of time nodes and the ones of interval lengths, the gradient equations for parameters were presented. The proposed method was demonstrated to have better approximation ability for the optimal control trajectories on two classic optimal control problems.

process control; control vector parameterization; variable time nodes; optimization; algorithm

2014-07-28.

Prof.LIU Xinggao, lxg@zju.edu.cn

10.11949/j.issn.0438-1157.20141128

TQ 021.8

A

0438—1157（2015）02—0640—07

国家自然科学基金项目（U1162130）。

2014-07-28收到初稿，2014-11-13收到修改稿。

联系人：刘兴高。第一作者：李国栋（1988—），男，博士研究生。

supported by the National Natural Science Foundation of China (U1162130).