锂离子电池基础科学问题(ⅩⅣ)——计算方法
2015-10-13凌仕刚王雪龙蒋礼威胡勇胜肖睿娟
黄 杰,凌仕刚,王雪龙,蒋礼威,胡勇胜,肖睿娟,李 泓
锂离子电池基础科学问题(ⅩⅣ)——计算方法
黄 杰,凌仕刚,王雪龙,蒋礼威,胡勇胜,肖睿娟,李 泓
(中国科学院物理研究所,北京 100190)
基础理论的创新与计算机性能的大幅度提升为高精度与多尺度的计算模拟提供了可能,这些方法也在锂离子电池的研究中得到了广泛的应用。本文介绍了第一性原理、密度泛函理论、分子动力学、蒙特卡罗、相场模拟、分子力场、有限元等不同时间与空间尺度上的模拟方法的基本原理,并探讨了这些方法在锂离子电池基础研究中的应用,如计算电池电压、电极材料的电子结构、能带结构、迁移路径、缺陷生成能、离子在材料体相及不同微观结构中的输运、材料中温度场分布、应力场分布等。
计算方法;密度泛函;分子动力学;经典模拟;锂离子电池
计算材料学(computational materials science)是材料科学与计算机科学相互交叉而形成的一门新兴学科,主要用于材料中结构、物性的设计与计算模拟,涉及物理、化学、计算机、材料学、数学等多个学科领域[1]。
近年来,随着基础理论的创新与计算机性能的大幅度提升,计算材料学也得到了快速的发展[2]。根据所研究问题的内容与所在的空间与时间尺度,计算材料学的模拟方法涵盖了从微观原子、分子水平,到介观微米级别,直至宏观尺度的各种理论。图1展示了不同尺度上的主要模拟方法[3].
计算材料学的迅速发展极大地促进了能源材料的研发进程[4]。锂离子电池作为绿色储能器件之一,虽已商业化,然而其中涉及的诸多基础科学问题仍不明朗,如SEI的生长机制、离子在电极材料中的扩散动力学特性、电极材料充放电过程中结构的演变、电位与结构的关系、空间电荷层分布等。实验探测手段如飞秒技术、高分辨透射电镜及X射线断层扫描(X-CT)等可以进行超快过程、原子尺度及三维立体原位成像等高分辨的时间与空间表征,但实验方法也往往有误差、难以观察、实验存在困难以及实验结果反映信息的片面性、不确定性的缺点,准确理解处于平衡态与非平衡态的锂电池内部的物理化学信息及演化规律,仍然需要理论上的解释,以获得更为本质的认识。
理论计算模拟有助于帮助人们更清楚地了解电池充放电过程中伴随着结构和性质变化所发生的电荷转移、质量转移、化学反应等过程;从而从微观上理解实验现象,寻找材料结构与性能之间的关系,同时也为电池材料的开发及电池行为的模拟提供理论依据。
本文将从原子尺度、介观尺度和宏观尺度三个方面分别介绍理论模拟方法在锂离子电池研究中的应用。
1 原子尺度的模拟
材料微观尺度的计算模拟依赖于理论模型对电子、原子之间相互作用势的描述。根据势函数模型中涉及到的参数数量及类型,可分为经验模型、半经验模型及量子力学模型。依赖的经验参数愈少,模型对体系的描述愈接近实际,理论可有效描述的范围也越广。基于量子力学的理论方法,在一定的假设条件下,从薛定谔方程出发,其计算的可靠性已在各个材料领域的研究中得到证实[2]。伴随着计算精度的提高,计算量也迅速增加,近几十年来的理论创新与计算机技术的革新为基于量子力学的第一性原理计算提供了可能。
第一性原理计算的宗旨是不采用任何经验参数,只采用电子质量、光速、质子质量、元电荷、普朗克常数5个基本物理量计算研究微观粒子的行为。第一性原理计算方法有着半经验方法不可比拟的优势,只需知晓构成微观体系的元素及其位置,即可以应用量子力学来计算出该微观体系的总能量、电子结构等物理性质。一方面,第一性原理计算可作为真实实验的补充,通过计算可以更为深入地理解被模拟体系的特征和性质;另一方面,通过第一性原理计算可以在尚无实验的情况下对研究体系进行预测和设计[2]。
近年来,第一性原理计算,特别是基于密度泛函理论的第一性原理计算同分子动力学、蒙特卡罗方法相结合,在材料设计、合成、模拟计算和评价诸多方面有许多突破性的进展,已经成为原子尺度上材料计算模拟的重要基础和核心技术。本部分将介绍第一性原理计算、分子动力学、蒙特卡罗等原子尺度的材料模拟方法在锂离子电池研究中的 应用。
1.1 基于密度泛函理论的第一性原理计算
密度泛函理论的建立始于20世纪60年代,经过数十年的发展,基于密度泛函理论的第一性原理计算已成为当今计算材料科学的一个最为重要的工具。1985年,Car和Parrinello两人把分子动力学方法和第一性原理计算结合起来,使得第一性原理方法在处理问题时变得更为实际[5]。1998年,Kohn教授[6]因其对密度泛函理论(DFT)发展所做出的巨大贡献荣获了该年度的诺贝尔化学奖。自此,计算材料学特别是基于密度泛函理论的第一性原理计算在材料科学研究中迅速升温。本节将主要针对密度泛函理论的基本原理及其在锂电池中的应用展开论述。
1.1.1 密度泛函理论(density functional theory)[7]
1.1.1.1 绝热近似
根据量子力学理论,微观粒子的运动规律用薛定谔方程来描述
波函数随时间的演化为
式中,为体系的总能量。上述定态薛定谔方程式(2)的求解仍然十分困难,特别是对于宏观体系原子数目高达1023数量级,精确求解方程式(2)几乎不可能。为此,必须做近似处理。由于原子核的质量比电子大得多,电子的运动速度要远高于原子核,可以近似认为原子核每移动一步,电子都能迅速弛豫到能量最低状态。这样就可以将原子核与电子的运动分开计算,这就是玻恩·奥本海默近似(Born Oppenheimer approximation),也称为绝热近似[8]。
玻恩·奥本海默近似的要领为:①将固体整体的平移、转动和核的振动运动分离出去;②考虑电子运动时,将坐标系原点设定在固体质心上,并令其随固体整体一起平移和转动,同时令各原子核固定在它们振动运动的某一瞬时位置上;③考虑核的运动时则不考虑电子在空间的具体分布。这样,通过分离变量即可写出电子分系统满足的Schrödinger方程
式中,e为电子动能项,ee为电子间库仑相互作用,为电子-原子核之间的库仑相互作用。
尽管通过绝热近似将包含原子核与电子体系的定态薛定谔方程简化为只对电子求解,然而对于较大体系的精确计算仍然非常困难。密度泛函理论(DFT)为简化这一问题提供了解决方案。
1.1.1.2 Hohenberg Kohn定理
密度泛函理论的核心思想是体系的所有物理性质都由其电子密度的空间分布所决定,即所有性质都是电荷密度函数的泛函,该理论思想最早由Thomas[9]和Fermi[10]于1927年提出。对能量泛函变分可求得能量极小值对应的电荷密度分布,这时对应的能量也即基态能量。泛函极小问题也是对电子密度分布函数求解。这样的处理首先要从理论上证明的确存在总能对于电子密度分布的这样一个泛函。因此Hohenberg和Kohn基于他们的非均匀电子气理论,提出了如下两个定理[11]。
定理1 不计自旋的全同费密子系统的基态能量是粒子数密度函数()的唯一泛函。
定理2 能量泛函()在粒子数不变的条件下,对正确的粒子数密度函数()取极小值,并等于基态能量。
这里所处理的基态是非简并的,多电子体系Hamilton量分开写作动能部分、多电子系统相互作用部分和多电子系统之外的外场部分
=++(5)
则Hohenberg-Kohn定理证明体系总能存在对基态电子密度分布函数的泛函形式
1.1.1.3 Kohn-Sham方程
尽管Hohenberg-Kohn定理证明了总能可通过求解最有利的基态电子密度分布函数所得到,但总能对于电子密度分布函数的具体泛函形式以及如何才能利用上述泛函极值的性质求解总能的问题,Hohenberg-Kohn定理并未给出回答。Kohn和Sham随后提出的Kohn-Sham方程最终将密度泛函理论引入了实际应用的行列。
Kohn-Sham方程的基本演绎过程如下[12]。
第二,假设动能部分和势能部分可进一步显式的写成
则整个能量泛函就可显式的表示为
式(11)与真实的多体系统能量泛函相比是有差别的。
变分的结果得到单电子形式的方程组,称为Kohn-Sham方程
1.1.1.4 交换关联函数
更精确的考虑需要计入某处附近的电荷密度对交换关联能的影响,如考虑到密度的一级梯度对交换关联能的贡献,称之为广义梯度近似 (generalized gradient approximation,GGA)[17]。这种近似是半局域化的,一般地,它比LDA更能给出精确的能量和结构,对开放的系统更为适用。目前常用的GGA方法有Becke、Perdew-Wang 91以及BLYP等形式[18-21]。
更进一步地,还可以考虑到密度高阶梯度的近似,这称为Meta-GGA或Post-GGA[22];甚至考虑到非局域的交换关联作用,如Van der Waals[23-24]作用。这两方面虽有研究,但仍未找到一个足够精确又简单的形式。
概括来说,LDA 与GGA各有所长,一般规律是LDA 倾向于将体系描述的过于局域化,而GGA 则过于离域化。因此,LDA通常低估晶胞参数,而GGA 则会高估晶胞参数。此外,在密度泛函理论基础上引入Hartree-Fock方程中精确的电子交换作用,被称为混合密度泛函(Hybrid-GGA)[25]。
1.1.1.5 自洽计算
在实际计算中,将多体系统原胞划分为足够细的网格点,在每个网格点上初始化一组试探波函数(通常设为随机数),然后根据式(15)可以算出网格上的Kohn-Sham势,本征方程式(14)立即可解。解出来的本征函数的值与初始化的值一般不相同,将新解出来的波函数的一部分叠加到初始值上,重新计算Kohn-Sham势式(15),利用修正过的势再次求解本征方程。 所得到的本征函数又用于修正上一步循环输入的波函数式······,循环叠代的结果是最终不再变化,计算得以收敛。利用收敛后的这组单电子波函数,立即得到体系总能量和电荷密度分布,图2示意了整个自洽计算求解Kohn-Sham方程的迭代过程[7]。
1.1.1.6 基于密度泛函理论的计算软件
目前使用DFT进行计算的软件非常多,如ABINIT(开源,免费),CASTEP(商业软件,仅对英国学院用户开源免费),DMol3(商业软件),Gaussian(商业软件),Quantum ESPRESSO(开源,免费),SIESTA(学院用户开源,免费),VASP(商业软件)及WIEN2k(商业软件)等。
1.1.2 密度泛函理论在锂电池研究中的应用
密度泛函理论在锂离子电池基础研究中有着广泛的应用,常用于计算电极材料的结构稳定性、嵌锂电位、电子结构、能带、弛豫结构、缺陷生成能、迁移路径、活化能及锂离子传输动力学和脱嵌锂相变等性质[26]。
1.1.2.1 嵌锂电位
电池的电压值是与电池反应的自由能变化相联系的参量。一个能自发进行的电化学反应,在等温可逆的条件下进行,当电池以无限小电流放电时,可对外做最大有用电功。由于电功=电压×电量,电量可按电池反应计算,1 mol电子电量称为1 法拉第(Faraday),以表示。一个电子e-的电量为1.602×10-19C,故有
=A·e-=96487.56 C/mol (17)
设为电池反应过程中转移的电荷数,则通过电池的电量为,电池所做最大电功为
-W'=AVE(18)
在等温等压条件下,体系的吉布斯自由能等于体系对外界所做的功
Δ=-W' (19)
所以
Δ=AVE(20)
又由于Li+带一个单位的电荷,因此
AVE=Δ/(21)
Δ是电池反应的吉布斯自由能,假设由电池嵌入反应引起的体积和熵的变化可忽略不计,则
Δ≈Δ(22)
故
AVE=Δ(23)
对于正极为LiA,负极为B的电池体系,假设充电后有个锂从LiA中脱出并嵌入到B中(正极充电过程),其反应式为
这一过程的平均电压为每个锂对应的末态(Li1-A,LiB)与初态(LiA,B)的能量之差,则电压
=[(Li1-xA)+(LiB)-(LiA)-(B)]/e (25)
如果负极为金属锂,则式(25)可简化为
=[(Li1-xA)+(Li)-(LiA)]/e (26)
研究早期人们发现,几乎对所有的正极材料,密度泛函理论计算得到的电压都偏低。Zhou等[27]认为这是由于含有3d过渡金属离子的正极材料属于强关联电子体系,其3d轨道的电子是高度局域化的。而在单电子近似的密度泛函理论框架下,局域化的电子会引入自相互作用,因此导致嵌锂电位被低估。通过对标准的GGA进行+U修正,也即GGA+U的方法,或采用杂化泛函HSE06,计算得到了与实验值更为接近的电压(图3)。在含有3d过渡金属离子的氧化物正极材料计算中,强关联效应已经公认为需要考虑的效应[28]。
1.1.2.2 电极材料的稳定性
在锂离子电池材料中,目前所使用的正极材料仍是锂源的主要提供者。若材料的主体框架在锂离子脱嵌的过程中无法稳定存在,则会导致电池性能的迅速衰减,甚至带来安全隐患,故研究电极材料的稳定性十分必要。
电极材料稳定性的预测主要基于材料热力学性质的计算。大量实验证据已经表明,层状正极材料LiCoO2、LiNiO2、LiMn2O4中,当锂的脱出量达到一定程度,材料会发生分解,转变为热力学上更为稳定的尖晶石相或岩盐相[29]。Wang等[29]计算了LiCoO2、LiNiO2、LiMn2O4材料在不同Li含量下的热力学相图,阐明了这3种材料的分解机制。以LiNiO2为例,Wang等计算了该材料在0 K、220 K、730 K的Li-Ni-O2三元相图(图4)。通过分析相图中LiNiO2稳定存在的区域及分解所经过的区域,认为LiNiO2的分解是通过层状向尖晶石相的放热反应和尖晶石向岩盐相的吸热反应两步来实现的。
除了脱嵌锂过程中的分解问题,电极材料在循环过程中的不稳定性还可能以氧析出的形式表现出来,这种现象在富锂相正极材料中较为常见[30]。富锂锰基Li2MnO3·(1-)LiMO2(M=Ni、Co、Mn等)正极材料因其高容量而受到广泛的研究。然而,由于氧气释放、低的电子电导等问题导致其具有高的不可逆容量和较差的倍率性能及循环性,阻碍了该类材料在实际中的应用。Xiao等[31]通过第一性原理计算系统地研究了富锂锰基正极材料的母相化合物Li2MnO3晶格中氧在不同锂含量时的稳定性。图5为通过第一性原理计算得到的不同脱锂态Li2−xMnO3氧气释放过程中的反应焓和吉布斯自由能。由图5可知,当脱锂量³0.5时会有氧气产生,进而导致结构的变化。
为改善富锂锰基Li2MnO3·(1-)LiMO2(M=Ni、Co、Mn等)正极材料充放电过程中因氧析出导致的结构不稳定,包覆和掺杂通常成为必要的手段。理论计算方面,Gao等[30]通过第一性原理计算研究了不同晶格位Mo掺杂Li2MnO3晶体的结构稳定性及Li+在晶格中不同跃迁方向的迁移能垒。图6是采用PBE+U交换关联势计算得到的不同脱锂态的LiMnO3和LiMn0.75Mo0.25O3的氧气释放过程中反应焓和吉布斯自由能[30]。分析图6可知,与未掺杂的Li2MnO3相比,掺Mo的Li2MnO3结构稳定性有了大幅度提升。
1.1.2.3 电子结构
电池材料的电子结构也与材料的电化学性能有着密切的关系。电极材料中,脱嵌锂过程中电荷补偿的来源和氧的稳定性与过渡金属及氧的分波态密度的相对位置有关[32],电极与电解质界面的化学稳定性则可从能态密度中做出定性预测[33],此外电池的倍率性能也与电极的电子导电性有关[34]。电池中的固态电解质材料需要具有电子绝缘的特性,材料的能隙宽度与其电化学窗口的宽度有关[35]。
电极与电解质之间的界面问题一直是电池研究中的难点。Lepley等[33]尝试通过理论计算理解Li3PS4和Li3PO4与金属Li负极之间的化学稳定 性[33]。图7和图8分别为计算得到的β-Li3PO4、γ-Li3PS4与金属Li界面模型的分波态密度图[33]。图中显示,当β-Li3PO4与金属Li接触时,金属Li的电子态分布在P和O的占据态的上方,与P、O原子之间难以相互作用,因此β-Li3PO4/Li界面的化学稳定性较高;而γ-Li3PS4/Li的界面上,Li的电子态与S的电子态之间有显著地重叠,二者之间容易发生电子转移,形成Li-S键,造成界面层形成新相,从而引起更为复杂的电化学过程。
1.1.2.4 离子输运机制
锂离子的传输是锂二次电池中核心的输运过程,锂离子传输的路径、能量势垒等与电池的倍率性能、极化程度、离子互占位等现象有着直接的联系。锂离子在材料中的扩散性质一方面可以通过基于过渡态理论的弹性能带方法(NEB)获得,另外也可以采用基于第一性原理的分子动力学方法计算得到。
Ouyang等[36]通过第一性原理计算研究了锂离子在橄榄石结构的LiFePO4中的扩散机理。通过对不同的可能扩散路径的迁移势垒的计算,表明对于LiFePO4、FePO4及Li0.5FePO4来说,扩散势垒沿着轴方向分别为0.6、1.2和1.5 eV。而在沿着轴、轴方向的迁移路径上,其扩散势垒非常大,以至于锂离子[37]难以扩散。这说明锂离子在LiFePO4中的扩散是一维的。这种一维的扩散行为通过第一性原理的分子动力学模拟得到了更进一步的验证,并且直观地观察到了锂离子的一维扩散行为[38]。
为了进一步解释Cr在Li位掺杂的LiFePO4材料电子电导率得到了大幅度提高而其电化学性能却没有得到明显改善的现象,Ouyang等[36]计算研究了纯的和Li位掺Cr的LiFePO4中锂离子和铬离子沿着一维扩散通道输运的能量势垒(图9所示分别为Li与Cr沿着轴方向的迁移势垒),结果发现锂离子可以很容易地沿着扩散通道扩散,但是铬离子很难离开本来的位置。这意味着铬离子堵塞了材料的一维扩散通道,如图10所示。从不阻塞一维离子输运通道的角度出发,他们考虑了低价态Na+的Li位掺杂以及其它金属离子的Fe位掺杂对材料动力学性能的影响,并发现两种方法都能够不同程度地提高材料的电子电导率,且不会阻塞Li+的一维输运通道。
1.1.2.5 缺陷生成能
材料中的缺陷和杂质会改变材料的许多性质,包括电子电导、离子电导等与锂电池性能紧密相关的性质。Hoang等[39]通过第一性原理计算研究了橄榄石结构的LiFePO4中的本征缺陷及掺杂对其电子传导和离子传导的影响。计算结果表明,在LiFePO4中本征的锂空位缺陷和空穴小极化子分别决定着材料的离子输运和电子输运过程。对一价掺杂元素(Na、K、Cu、Ag),二价掺杂元素(Mg、Zn),三价掺杂元素(Al),四价掺杂元素(Zr、C、Si)和五价掺杂元素(V、Nb),Hoang等[39]分别计算了各种元素掺入不同晶格位置的缺陷形成能,不同合成条件对掺杂浓度的调节以及掺杂后对体系输运性质的改变,发现通过缺陷控制的合成手段可能有效地改善体系的电子导电性。
1.1.2.6 晶体结构及演化
电极材料在脱嵌锂的过程中,有时会出现一些有趣的结构演化过程,如在石墨嵌锂过程中出现的“阶”结构[40]。近年来,随着透射电镜技术的发展,人们在LiFePO4的脱锂样品中观察到了三相界面,并且也发现了“阶”的现象[41]。借助原子尺度的计算模拟,该结构的演变过程及形成机制得到了进一步的阐释。
Sun等[42]通过第一性原理计算研究了LiFePO4脱锂过程中出现的“阶”结构(图11)。结果显示,“阶”结构是一种受Li+传输动力学控制的热力学亚稳态。其成因在于,当一层锂脱出后其最近邻锂层的Li+跃迁受到阻碍,因此充电过程中倾向于隔层脱锂而不是顺序脱锂。结合热力学条件,Sun等[42]构建了一个用来描述LiFePO4充电过程的双界面脱锂模型:充电时,LiFePO4颗粒中同时存在两个隔层脱锂过程,它们在空间上有一定的相位差;经历过两个隔层脱锂过程的区域为FePO4相,只经历过一个隔层脱锂过程的区域为“阶”结构,而两个隔层脱锂过程都没有经历过的区域为LiFePO4相。脱锂过程中“阶”结构位于LiFePO4与FePO4两相之间,该理论模型很好地解释了高分辨扫描透射电镜下观察到的现象[41]。
“阶”结构的形成表明,LiFePO4中Li+的占据与否会影响其最近邻锂层的Li+传输。由于LiFePO4是一个强关联电子体系,Fe 3d轨道电子高度局域,Li+占据/缺失带来的电子/空穴会局域在最近邻的铁离子上。因此,Li+可以通过改变其最近邻铁离子的价态来影响近邻锂层中的Li+传输行为。实际上这是一种以铁离子为媒介的层间Li+间接相互作用,而之前的计算研究主要局限于Li+之间的直接作用。Sun等的计算结果说明,对于电子高度局域的强关联电子体系,除了离子之间的直接相互作用,还需要考虑可能存在的间接相互作用。对于两/多相分离反应,在计算其离子传输性质时需要考虑相界面附近的离子相互作用[26]。
1.1.2.7 材料力学性能
大多数电极材料在反复的脱嵌锂过程中会经历体积的变化,如层状材料在脱锂后会出现沿方向的膨胀,Si负极在嵌锂之后则会出现多达300%的体积膨胀[43]。这就需要我们对材料的力学性能进行进一步研究,以理解材料在脱锂过程中形变产生的原因及对电池性能的影响。基于密度泛函理论的第一性原理能够通过求解力矩阵,获得材料的弹性常数,从而得到体模量、剪切模量、杨氏模量、泊松比等一系列力学性能的数值[44]。
Shenoy等[45]计算了不同Li含量的Li-Si合金的力学性质,建立了Si负极嵌锂过程中形变与断裂过程的力学模型。通过计算晶态与非晶态Li-Si合金相的杨氏模量、剪切模量、体模量和泊松比(图12),他们发现随着锂浓度的增加,上述模量值几乎呈线性降低,表明嵌锂引起了材料的弹性软化,同时也说明了材料的力学特性在电池的电化学过程中不是保持不变的,应力场的分布与形变及裂纹的扩展都与充放电状态相关。
1.2 分子动力学
基于密度泛函的第一性原理计算能够得到材料处于零温基态时的性质,这对理解材料的本征特性非常重要。在有限温度下材料中原子、离子的输运可通过分子动力学模拟进行研究。本节将介绍分子动力学方法及其在锂离子电池中的应用。
1.2.1 分子动力学方法介绍[46]
分子动力学方法是一种模拟经典系统平衡态和输运性质的一种技术,经典系统的粒子运动规律为牛顿力学
多粒子耦合
求解式(28)方程组需设定粒子的初始位移和速度,通过实验,如X射线衍射以及核磁共振技术等,可以确定原子的初始位移。而初始速度通常按照一个温度关联的随机分布函数分布,对分布函数进行修正,使得总动量为零。
通常速度分布可选择Maxwell-Boltzmann 分布。在一定的温度下,分函数给出某个粒子在方向上具有速度的概率为
知道粒子的初始位移和速度,计算出每个原子所受的力,按牛顿定理离散的形式
分子动力学中按照力的计算方法不同分为经验势方法(MD/MM等)、半经验势方法(TBMD等)和第一性原理分子动力学(FPMD)[47]。
对于经验势方法MD/MM等,不直接考虑电子体系使用经验势,可计算很大接近宏观的体系。
半经验势方法TBMD等,对电子采取紧束缚近似,可计算较大的体系。
第一性原理方法,如QMD、CPMD、FPMD,电子和核都用比较准确的研究和计算方法,计算量大,只能研究小体系。
1.2.2 分子动力学模拟所获得信息
分子动力学模拟可以获得包括原子的位置和运动速度等原子尺度的信息。统计力学能把这些原子尺度的信息转换为宏观可观测量,如能量、比热容、压强等。这样的转换基于各态历经假设(ergodic hypothesis),即统计系统平均等效于对时间的平均。
最基本的思想是:分子动力学的目的是通过模拟系统在足够长时间里系统随时间的演化过程,从而产生足够多的满足我们需要的相空间的各种构型,然后对这些构型进行平均,得到诸如结构、动力学、热力学等宏观性质。在锂离子电池中我们主要希望获得材料中离子的扩散系数和迁移路径[48]。
由Fick第二定律可知
上述方程的解为
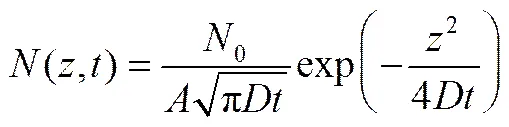
扩散系数的定义由爱因斯坦关系给出
为空间维度,忽略交叉项的平均得到
虽然分子动力学可以模拟系统粒子随时间的演化,查看离子迁移的路径,计算粒子的扩散系数以及材料的稳定性,但是粒子运动的规律是牛顿力学,对质量较轻的粒子比如氢气和氦低温存在量子效应计算效果不理想[49]。
1.2.3 分子动力学在锂电池中的应用
分子动力学不仅可以揭示材料中离子自扩散过程中的运动路径、能量势垒,也为我们理解材料中离子的扩散机制提供了可能。Yang等[50]通过计算LiFePO4的自扩散过程,发现该材料中Li+的迁移并不是连续发生的,而是如图12所示通过相邻晶格位置之间逐渐推进的跃迁发生的。Yang等[50]的模拟不仅发现了Li+沿着一维方向的“之字型”路径前进的过程,还发现了Li-Fe离子的协同运动,这种协同运动导致了Li/Fe互占位且有利于Li+在通道之间的扩散。
1.3 蒙特卡罗方法
1.3.1 蒙特卡罗方法的介绍
蒙特卡罗(Monte Carlo,MC)方法,又称随机抽样或统计试验方法,属于计算数学的一个分支,它是在20世纪40年代中期为了适应当时的原子能事业而发展起来的,学术界一般把1949年Metropolis 和Ulam发表的论文作为MC方法诞生的标志[51-52]。
知道物理规律,就能用蒙特卡罗方法模拟出满足物理规律的大量随机事件,由这些随机事件统计出需要计算的物理量的值。有些实验实施非常昂贵或非常危险,还有一些物理过程目前还无法探测,都可以用蒙特卡罗方法模拟出真实的过程。从数学的观点而言,统计就是求平均,因此蒙特卡罗方法能通过抽样的方法用于求解定积分。求解积分的统计基础是独立同分布中心极限定理(林德贝尔格-勒维定理),这个定理说明蒙特卡罗的积分标准方差和维度无关[53]。
如果已知事件的概率分布,需要采用抽样算法来获得满足这样概率分布的样本,以模拟真实的过程。常见的抽样方法有直接抽样法、舍选抽样法、复合抽样法、变换抽样法、近似抽样法、重要分布的随机抽样法和Metropolis 抽样方法[54]。物理中常用的抽样方法是Metropolis抽样,是一种非归一化的抽样方法。详细介绍可见参考文献[54]。Metropolis抽样方法的考虑是:不是独立地选择相继各种状态点,而是构造一个马尔可夫(Markov)过程,每个状态由前一个状态点通过一个适当的跃迁概率得到(=1, 2,…)。当→∞,Markov过程产生的状态的分布函数趋于平衡分布。
平衡态的概率分布为
要达到上式的平衡分布,通常还必须加上细致平衡条件
即两个状态正向与反向的跃迁概率之比只依赖于两者的能量差d=(x)(x)。式(41)不能唯一地确定跃迁概率,通常可以选择
对于正则系综,MC模拟的基本步骤为:① 随机选择一个初始位形;② 利用随机数,产生一个新的位形;③ 计算能量变化;④ 若d<0,接受新位形并回到第2步,否则继续进行下一步;⑤ 计算,并产生一个[0,1]之间的随机数;⑥ 如果,同样接受新位形,并回到第2步;⑦ 否则,保持原位形作为新位形并回到第2步。
以上步骤表明,对于一个能量低于原位形的新位形直接接受,而对于能量升高的位形,就按Boltzmann 概率接受。
1.3.2 蒙特卡罗方法在锂电池中的应用
SEI膜对电池的安全性、循环性、首周库仑效率等有着重要的意义[55]。Methekar等[56]通过动力学蒙特卡罗模拟充电放电过程中的副反应以及离子扩散等过程,观测到石墨表面SEI膜随着循环的次数增加而逐渐形成的过程。图15(a)表示首周循环后负极表面形貌,图15(b)为100周循环后的负极表面形貌,红色表示SEI膜,品红表示处于原始状态石墨表面,绿色表示吸附了金属锂位点[56]。
Ouyang等[37,57]采用蒙特卡罗的方法模拟了LiMn2O4在不同锂含量下材料的平衡态结构,计算了放电过程的电压,并模拟了升高温度后体系放电电压平台的变化(图16),采用蒙特卡罗的方法模拟了外电流和电压的关系,结果符合欧姆定律。
Ouyang等[58]还通过蒙特卡罗方法模拟了LiFePO4中掺杂Cr的情况,迁移出截面的Li+量随Cr含量变化,Cr含量越多,Li+量越少,电池容量越低,如图17所示。
基于密度泛函理论的第一性原理计算能从电子结构的层面揭示锂离子电池材料的结构、能带、缺陷、导电率、力学性质等本征特性,分子动力学和蒙特卡罗模拟等方法能在原子尺度研究材料的动力学性能,上述方法都有助于理解材料在电化学过程中表现出来的种种现象。这些计算方法所关注的是材料在空间尺度为10-10~10-9m,时间尺度为皮秒量级的过程。如果需要考虑尺度在10-9~10-3m,时间尺度在秒或者毫秒量级的问题时,则需要采用介观尺度的模拟方法。
2 介观尺度模拟
介观尺度指的是介于原子层次和连续体之间的区域,在这个空间尺度里主要关注的是微观组织随时间发生的演化,如晶体的生长凝固过程等。常用的模拟方法有相场方法[59]、分子力场方法[60]等。
2.1 相场模型
相场模型可用来处理纳米和微米尺度的结构演化,在该尺度范围内,材料的尺寸、形状、空间分布对材料的物理性质和化学性质起着重要的作用。微结构演化实际是自由能减少的过程,材料的自由能是体相化学能、界面能、弹性应变能、磁性能、静电能以及外加电场作用能的共同贡献。相场模型是建立在界面扩散的基础之上,微结构随时间的演化是连续性方程,即Cahn-Hilliard 非线性方程和时间依赖的Ginzburg-Landau方程[61]。相场方法模拟的介观尺度的现象包括晶粒生长和粗糙化、材料成型、裂纹演化、位错和溶质的相互作用、电迁移和多组分互扩散等过程[62-63],这些过程在锂离子电池中都可能发生,并直接影响电池的循环性、倍率性、安全性等。
相场方法中,微观结构用一个连续变量序参数来表示。如0、1以及0<<1分别代表沉积相、基体、界面。
2.1.1 相场模型的基本原理
在相场模型中,将总自由能表示为式(43)形式[49]
在相场模型中演化方程[59]
式中,M和pq是原子或者界面的扩散速度。建立模型后就能根据式(43)、式(44)导出动力学方程,可将上述微分积分方程转化为代数方程,也可在实空间离散化[59]。通过相场模型虽然能够模拟晶体生长、固态相变、裂纹演化、薄膜上的相变、离子在界面处迁移等,但是模拟结果缺少和时间观测量的定量比较,计算时界面厚度的设定通常大于实际情况,导致细节的缺失。
2.1.2 相场方法在锂电池研究中的应用
Yamakawa等[65]通过相场方法模拟层状正极材料LiCoO2不同晶粒大小、不同晶粒取向对Li+扩的影响。图19为模拟得到的在恒流放电时LiCoO2中Li浓度的空间分布。显示出Li+的扩散对晶界、晶体方向的空间分布及晶粒的尺寸都十分敏感。
锂离子电池中还有很多现象可以通过相场模拟获得进一步的认识。如在纳米硅负极材料的充放电过程中伴随着材料的体积膨胀,会导致黏结剂的脱落,SEI重新生成和容量衰减[66],Zuo等[64]通过相场模型研究硅薄膜在嵌锂过程中力场分布以及裂纹的演化过程。
2.2 分子力学
分子力学,也叫力场方法(force field method),常用于计算化学和生物大分子等的结构和能量,也可以用于研究锂离子电池中的电化学过程。
2.2.1 分子力学方法的介绍[60]
分子力学方法中,在考虑几何结构或力学特性等静态性质时,将原子与原子之间的作用视为主要的相互作用。因此在分子力场模型中,把组成分子的原子看成是由弹簧连接起来的球,然后用简单的数学函数来描述球与球之间的相互作用。
分子力场函数一般可以表达为
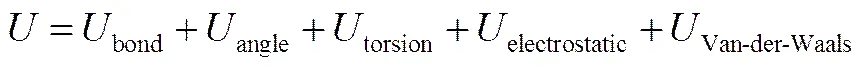
式中,前3项分别代表键伸缩能、键角弯曲能和二面角扭曲能,是描述分子内成键的作用项。后两项为静电作用和范德瓦尔斯作用,是描述分子间的非键相互作用。
构成一套力场函数体系需要有一套联系分子能量和构型的函数,还需要给出各种不同原子在不同成键状况下的物理参数,如正常的键长、键角、二面角等,都是通过拟合特定分子的数据而生成的,这些被拟合的分子称为训练基(training set)。这些力场参数多来自实验或者量子化学计算。由于力场参数是拟合训练基分子得到的,并且所拟合的实验数据是常温常压下测量的,所以这些参数用于计算其它分子或者高温高压情况,分子力学的准确性会降低。
2.2.2 分子力场方法在锂电池中的应用
Garofalini等[67]利用分子力场方法研究了锂离子电池里,当金属锂嵌入纳米材料FeF2发生转化反应的作用机理。通过利用合理的经验势函数模型以及相关参数模拟FeF2+2Li==2LiF+Fe相转变过程中的动力学过程,图20显示了在FeF2(001)表面上发生的反应过程[67]。图中Fe原子、F原子和Li原子分别用绿色、黄色和红色表示,整个FeF2表面上有4320个原子,这4幅图分别表示有72、288、360、864个Li进入FeF2表面进行相转变的过程。可以明显地看到随着越来越多Li进入,金属Fe团簇和晶体状的LiF都在各自形成。
相场方法和分子力场方法可用于研究微观结构及其演化过程对锂离子电池性能的影响,对于更大空间尺度上(10-6~100m)的问题,体系的随机性不明显,可以采用下文介绍的基于连续体模型的宏观尺度模拟方法。
3 宏观尺度模拟
在宏观尺度上,体系的运动力学遵循牛顿力学方程,热运动满足宏观的扩散方程,可以采用的数值模拟方法包括有限元方法[68]、有限差分方法[69]等,其中有限元方法常用来研究锂离子电池中的热流分布[70]、应力分布[71]等现象,本节将主要介绍有限元方法及其在电池材料研究中的应用。
3.1 有限元方法介绍
有限元方法(finite element method)是一种求解偏微分方程边值问题近似解的数值技术,如求解电池内部的热、力、电流、电压的分布等都需要求解在特定边界条件下的输运方程。而这些方程的精确求解几乎是不可能的。人们通常采用两种方法去逼近真实的解:全域的展开逼近,典型代表为傅里叶级数展开;基于子域的分段函数展开,如有限 元[68]。后者将求解域看成是由许多简单而又相互作用的元素的互连子域组成(单元),对每一单元假定一个合适的(较简单的)近似解,然后推导求解这个总域满足条件(如结构的平衡条件),从而得到问题的解。这两种方式各有特点,全域的方法采用高次连续函数,通过几个基底函数得到很好的效果。第二种方法要通过较大的工作量才得得到较好的效果。但是能将复杂方程的解化繁为简,使得描述和求解成为可能。
有限元方法模拟的流程可以概括为[68]:首先对求解问题区域离散化,然后确定这个区域的状态变量和变量的控制方法即变量时间空间的演化方程,然后对单个单元进行推导,之后对由单元组装起来的总体进行求解,最后联立方程组求解并获得结果。
3.2 有限元方法在锂电池研究中的应用
对于高功率的动力电池而言,电池内部温度分布对其安全性和寿命有重要影响。西安交通大学曹秉刚等[70]在考虑内阻、对流、外部耗散等条件下利用有限元方法模拟了电池工作时内部温度的空间分布,以及在155 ℃热炉中测试电池的温度分布(图21),模拟结果和VLP50/62/100S-Fe(3.2 V/55 A·h) LiFePO4/石墨的电池复合。
Bower等[71]利用有限元的方法研究了嵌锂后硅颗粒内力分布。图22显示了采用有限元方法模拟的薄膜非晶硅电极在充放电循环过程中的应力分布及形变和断裂过程。
宏观尺度的材料模拟着眼于工程领域的问题,可以有助于理解锂离子电池中出现的应力、传热、流动以及多场耦合等宏观现象。
4 结 语
随着各种理论的完善和计算机技术的发展,计算模拟已经成为锂离子电池研究中的重要方法之一。不同时间与空间尺度的模拟方法有助于我们从原子分子层次、介观层次和宏观层次理解材料结构与性能之间的关系。而这些不同尺度上的计算方法可以通过参数传递进行联系,从而实现材料的多尺度模拟[2],为材料设计提供了一种新的途径。通过实验与理论计算相结合的方法,有望解决的锂离子电池研究中的关键科学问题如下。①设计出新的电极与电解质材料:找到一些目前尚未发现的锂离子电池材料,并且具有更好的性能与更高的安全性;目前正在发展的材料基因组方法是锂电池计算方面发展的重要方向。②理解体相电极材料反应的热力学问题,通过精确计算材料的反应生成焓,预测材料在各种条件,如不同温度、不同压力、不同组分下的稳定性,甚至建议材料的合成方案。③理解电位与材料组成、微观结构的关系。通过计算与实验得到大量已知结构及新结构所对应的电化学电位,建立电位与结构关系的数据库,采用统计方法,寻找决定电位的因素,理解它们之间的物理关联。 ④电极材料充放电过程中组成与结构演变,通过计算得到的生成焓数据,建立与电极变化过程有关的相图,分析电极材料结构演变对稳定性的影响,理解影响电极循环性能的因素以及电极材料的失效机制。⑤与电池有关的复杂过程的理解,如输运性质、尺寸效应、界面问题等复杂过程。⑥材料与器件制备过程、服役过程的数字化模拟与仿真。
对锂离子电池中这些基础科学与应用技术问题的理解,对全产业链过程的多尺度计算和模拟,最终有望加速锂离子电池以及下一代锂电池材料的开发过程,帮助我们更快找到高性能、高安全性的正极、负极与电解质材料,促进锂电池产业的发展。
[1] Jian Zengyun(坚增运),Liu Cuixia(刘翠霞),Lv Zhigang(吕志刚). Computational Materials Science(计算材料学)[M]. Beijing:Chemical Industry Press,2012.
[2] Hafner J,Wolverton C,Ceder G. Toward computational materials design:The impact of density functional theory on materials research[J].,2006,31(9):659-667.
[3] Wang C Y,Zhang X. Multiscale modeling and related hybrid approaches[J].,2006,10(1):2-14.
[4] Meng Y S,Dompablo M E. Frist principles computational materials design for energy storage materials in lithium ion batteries[J].,2009,2(6):589-609.
[5] Car R,Parrinello M. Unified approach for molecular dynamics and density-functional theory[J].,1985,55(22):2471-2474.
[6] Kohn W. Nobel lecture:Electronic structure of matter—Wave functions and density functionals[J].,1999,71(5):1253-1266.
[7] Shi Siqi(施思齐). 锂离子电池正极材料的第一性原理研究[D]. Beijing:Institute of Physics Chinese Academy of Sciences,2004.
[8] Born M,Huang K. Dynamical Theory of Crystal Lattices[M]. Oxford:Oxford Universities Press,1954.
[9] Thomas L H. The calculation of atomic fields[J].,1927,23(5):542-548.
[10] Fermi E. Un metodo statistico per la Determinazione di alcune prioprietà dell'Atomo[J].,1927,6:602-607.
[11] Hohenberg P,Kohn W. Inhomogeneous electron gas[J].,1964,136(3B):864-871.
[12] Kohn W,Sham L J. Self-consistent equations including exchange and correlation effects[J].,1965,140(4A):1133-1138.
[13] Slater J C. A simplification of the Hartree-Fock method[J].,1951,81(3):385-390.
[14] Ceperley D M,Alder B J. Ground-state of the electron-gas by a stochastic method[J].,1980,45(7):566-569.
[15] Perdew J P,Zunger A. Self-interaction corrction to density-functional appoximations for many-electron systems[J].,1981,23(10):5048-5079.
[16] Jones R O,Gunnarsson O. The density functional formalism, its application and prospects[J].,1989,61(3):689-746.
[17] Langreth D C,Perdew J P. Theory of nonuniform electronic systems.1.analysis of the gradient approximation and a generalization that works[J].,1980,21(12):5469-5493.
[18] Becke A D. Density-functional exchange-energy approximation with correct asymptotic-behavior[J].,1988,38(6):3098-3100.
[19] Perdew J P,Chevary J A,Vosko S H,. Atoms,molecules,solids,and surfaces—Applications of the generalized gradient approximation for exchange and correlation[J].,1992,46(11):6671-6687.
[20] Perdew J P,Wang Y. Accurate and simple analytic representation of the electron-gas correlation-energy[J].,1992,45(23):13244-13249.
[21] Perdew J P,Burke K,Ernzerhof M. Generalized gradient approximation made simple[J].,1996,77(18):3865-3868.
[22] Tao J,Perdew J P. Climbing the density functional ladder:Nonempirical meta-generalized gradient approximation designed for molecules and solids[J].,2003,91(14):146401.
[23] Andersson Y,Langreth D C,Lundqvist B I. Van der Waals interactions in density-functional theory[J].,1996,76(1):102-105.
[24] Kohn W,Meir Y,Makarov D E. Van der Waals energies in density functional theory[J].,1998,80(19):4153-4156.
[25] Becke A D. A new mixing of Hartree-Fock and local density-functional theories[J].,1993,98(2):1372-1377.
[26] Sun Yang(孙洋). 锂离子电池电极材料中离子传输与相变反应机理的第一性原理研究[D]. Beijing:Institute of Physics Chinese Academy of Sciences,2014.
[27] Zhou F,Cococcioni M,Marianetti C A,. First-principles prediction of redox potentials in transition-metal compounds with LDA + U[J].,2004,70(23):235121.
[28] Chevrier V L,Ong S P,Armiento R,. Hybrid density functional calculations of redox potentials and formation energies of transition metal compounds[J].,2010,82(7):75122.
[29] Wang L,Maxisch T,Ceder G. A first-principles approach to studying the thermal stability of oxide cathode materials[J].,2007,19(3):543-552
[30] Gao Y R,Ma J,Wang X F,. Improved electron/Li-ion transport and oxygen stability of Mo-doped Li2MnO3[J].,2014,2(13):4811-4818.
[31] Xiao R J,Li H,Chen L Q. Density functional investigation on Li2MnO3[J].,2012,24(21):4242-4251.
[32] Goodenough J B,Kim Y. Challenges for rechargeable Li batteries[J].,2010,22:587-603.
[33] Lepley N D,Holzwarth N A W,Du Y A. Structure, Li+mobilities, and interfacial properties of solid electrolytes Li3PS4and Li3PO4from first principles[J].,2013,88:104103.
[34] Shi S Q,Liu L J,Ouyang C Y,. Enhancement of electronic conductivity of LiFePO4by Cr doping and its identification by first-principles calculations[J].,2003,68(19):195108.
[35] Quartarone E,Mustarelli P. Electrolytes for solid-state lithium rechargeable batteries:Recent advances and perspectives[J].,2011,40(5):2525-2540.
[36] Ouyang C Y,Shi S Q,Wang Z X,. The effect of Cr doping on Li ion diffusion in LiFePO4from first principles investigations and Monte Carlo simulations[J].:.,2004,16(13):2265-2272.
[37] Ouyang Chuying(欧阳楚英). 锂离子电池正极材料离子动力学性能研究[D]. Beijing:Institute of Physics Chinese Academy of Sciences,2005.
[38] Ouyang C Y,Shi S Q,Wang Z X,. First-principles study of Li ion diffusion in LiFePO4[J].,2004,69(10):104303.
[39] Hoang K,Johannes M D. First-principles studies of the effects of impurities on the ionic and electronic conduction in LiFePO4[J]..,2012,206:274-281.
[40] Ohzuku T,Iwakoshi Y,Sawai K. Formation of lithium-graphite intercalation compounds in nonaqueous electrolytes and their application as a negative electrode for a lithium ion (shuttlecock) cell[J]..,1993,140(9):2490-2498.
[41] Gu L,Zhu C B,Li H,Yu Y,Li C L,Tsukimoto S,Maier J,Ikuhara Y. Direct observation of lithium staging in partially delithiated LiFePO4at atomic resolution[J].,2011,133(13):4661-4663.
[42] Sun Y,Lu X,Xiao R J,. Kinetically controlled lithium-staging in delithiated LiFePO4driven by the Fe center mediated interlayer Li-Li interactions[J].,2012,24(24):4693-4703.
[43] Li H,Huang X J,Chen L Q,Wu Z G,Liang Y. A high capacity nano-Si composite anode material for lithium rechargeable batteries[J].,1999,2(11):547-579.
[44] Stadler R,Wolf W,Podloucky R,. Ab initio calculations of the cohesive, elastic, and dynamical properties of CoSi2by pseudopotential and all-electron techniques[J].,1996,54(3):1729-1734.
[45] Shenoy V B,Johari P,Qi Y. Elastic softening of amorphous and crystalline Li-Si Phases with increasing Li concentration:A first-principles study[J].,2010,195(19):6825-6830.
[46] Frenkel D,Smit B. Understanding Molecular Simulation[M]. Newyork:Academic Press,2001.
[47] Richard M M. Electronic Structure:Basic Theory and Practical Methods[M]. Cambridge:Cambridge University Press,2004.
[48] Van der Ven A,Ceder G,Asta M,. First-principles theory of ionic diffusion with nondilute carriers[J].,2001,64(18):184307.
[49] Chen J,Li X Z,Zhang Q F,. Quantum simulation of low-temperature metallic liquid hydrogen[J].,2013(4):1-5.
[50] Yang J J,Tse J S. Li ion diffusion mechanisms in LiFePO4:An ab initio molecular dynamics study[J].,2011,115(45):13045-13049.
[51] Metropolis N,Ulam S M. The Monte Carlo method[J].,1949,44(247):335-341.
[52] Niederreiter H. Quasi-Monte Carlo methods and pseudo-random numbers[J].,1978,84(6):957-1041.
[53] Hoffmann K H,Meyer A. Parallel Algorithms and Cluster Computing:Implementations, Algorithms and Applations[M]. Berlin:Springer,2006.
[54] Binder K. Applications of Monte Carlo methods to statistical physics[J].,1997,60(5):487-559.
[55] Zheng J Y,Zheng H,Wang R,3D visualization of inhomogeneous multi-layered structure and Young's modulus of the solid electrolyte interphase (SEI) on silicon anodes for lithium ion batteries[J].,2014,16(26):13229-13238.
[56] Methekar R N,Northrop P W C,Chen K,. Kinetic Monte Carlo simulation of surface heterogeneity in graphite anodes for lithium-ion batteries:Passive layer formation[J].,2011,158(4):A363.
[57] Ouyang C Y,Shi S Q,Wang Z X,. Temperature-dependent dynamic properties of LiMn2O4in Monte Carlo simulations[J].,2005,22(2):489-492.
[58] Ouyang C Y,Shi S Q,Wang Z X,. The effect of Cr doping on Li ion diffusion in LiFePO4from first principles investigations and Monte Carlo simulations[J].:,2004,16(13):2265-2272.
[59] Chen L Q. Phase-field models for microstructure evolution[J].,2002,32(1):113-140.
[60] Cornell W D,Cieplak P,Bayly C I,. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules[J].,1995,117(19):5178-5197.
[61] Kobayashi R. Modeling and numerical simulations of dendritic crystal growth[J].:,1993,63(3-4):410-423.
[62] Jia Weijian(贾伟建). 凝固微观组织相场法模拟[D]. Lanzhou:Lanzhou University of Technology,2005.
[63] Long Wenyuan(龙文元). Phase-field simulations of dendritic growth in aluminum alloy solidification[D]. Wuhan:Huazhong University Science and Technology,2004.
[64] Zuo P,Zhao Y P. A phase field model coupling lithium diffusion and stress evolution with crack propagation and application in lithium ion batteries[J].,2014,17(1):287-297.
[65] Yamakawa S,Yamasaki H,Koyama T,Asahi R. Numerical study of Li diffusion in polycrystalline LiCoO2[J].,2013,223:199-205.
[66] Beaulieu L Y,Hatchard T D,Bonakdarpour A,. Reaction of Li with alloy thin films studied by in-situ AFM[J].,2003,150(11):A1457.
[67] Ma Y,Garofalini S H. Atomistic insights into the conversion reaction in iron fluoride:A dynamically adaptive force field approach[J].,2012,134(19):8205-8211.
[68] Wang Xucheng(王勖成). 有限单元法[M]. Beijing:Tsinghua University Press,2008.
[69] Zhang Wensheng(张文生). 科学计算中的偏微分方程有限差分方法[M]. Beijing:Higher Education Press,2006.
[70] Guo G F,Bo L,Bo C,. Three-dimensional thermal finite element modeling of lithium-ion battery in thermal abuse application[J].,2010,195(8):2393-2398.
[71] Bower A F,Guduru P R. A simple finite element model of diffusion, finite deformation, plasticity and fracture in lithium ion insertion electrode materials[J].,2012,20(4):45004.
Fundamental scientific aspects of lithium ion batteries(ⅩⅣ)—Calculation methods
HUANG Jie,LING Shigang,WANG Xuelong,JIANG Liwei,HU Yongsheng,XIAO Ruijuan,LI Hong
(Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China)
With the rapid development of modern physical theory and computational technology, computer simulations have become efficient methods in materials science, which are also extensively used in the study of lithium ion batteries. In this paper, we introduce the basic principles of commonly used calculation methods in different space and time scales, e.g.calculation, density functional theory, molecular dynamics, monte carlo, phase field simulation, force field and finite element method. Their applications in the fundamental research of lithium ion batteris, such as the calculation of the cell voltage, electronic sturcture, band gap, ion transport mechanism in bulk and various microstructures, and the distribution of temperature field and stress field in electrode materials, are also discussed.
calculation methods;density functional theory;molecular dynamics;classical simulation; lithium ion battery
10.3969/j.issn.2095-4239.2015.02.014
O 646.21
A
2095-4239(2015)02-215-16
2015-01-26;修改稿日期:2015-02-02。基金项目:国家自然科学基金杰出青年基金(51325206),重点基金(11234013)及国家重点基础研究发展计划(973)(2012CB932900)项目。第一作者:黄杰(1987—),男,博士研究生,研究方向为锂空气电池与理论计算模拟,E-mail:huangj08@126.com;通讯联系人:肖睿娟,副研究员,研究方向为锂电池材料的理论计算模拟,E-mail:rjxiao @iphy.ac.cn。
