一种基于SAPSO-DE混合算法的结构非概率可靠性优化设计
2015-10-13郑灿赫孟广伟李锋孔英秀金耿日
郑灿赫,孟广伟,李锋,孔英秀,金耿日
一种基于SAPSO-DE混合算法的结构非概率可靠性优化设计
郑灿赫1, 2,孟广伟1,李锋1,孔英秀1,金耿日3
(1.吉林大学机械科学与工程学院,吉林长春,130025;2. 理科大学力学学院,朝鲜平壤;3. 吉林大学汽车仿真与控制国家重点实验室,吉林长春,130025)
针对不确定性结构的非概率可靠性优化问题,提出一种基于模拟退火粒子群算法和差分进化算法(SAPSO- DE混合算法)的结构非概率可靠性优化设计方法。考虑结构非概率可靠性指标约束,建立最小化结构体积为目标的优化模型。为了提高结构非概率可靠性优化问题的计算精度和效率,采用基于认知经验进化的SAPSO-DE混合算法进行非概率可靠性优化设计。研究结果表明:基于SAPSO-DE混合算法的结构非概率可靠性优化设计方法克服了PSO算法的早熟现象,并提高了收敛速度和精度;该方法的全局搜索能力强,且具有较强的稳定性。
非概率可靠性指标;凸模型;不确定性;粒子群优化算法;差分进化算法;模拟退火
概率可靠性优化模型需要大量的不确定数据,预知不确定变量的分布状态,以确定其概率分布函数,且计算量较大[1]。为了克服概率可靠性优化模型的缺点,有些学者对非概率可靠性优化模型进行了研 究[2−11]。Ben-Haim等[2−4]采用凸模型来描述有界不确定变量,提出了非概率可靠性概念,建立了非概率可靠度的计算方法。Ganzerli等[5]将凸模型理论与结构的不确定优化设计相结合,通过叠加方法获取结构响应的极值,一定程度上减少了计算量。乔心州等[6−7]指出了基于区间模型的非概率可靠度较基于凸模型的非概率可靠度保守、基于凸模型的非概率可靠度更接近工程实际,进行了基于非概率集合可靠性的结构优化设计。曹鸿钧等[8]提出了超椭球凸模型和区间模型共存下的非概率可靠性指标,建立了以可靠性指标为约束的结构非概率可靠性优化模型,并采用一种序列线性化方法求解结构非概率可靠性优化问题。王晓军等[9]考虑结构参数不确定性,提出了基于非概率可靠性的结构优化方法,进行了一桁架结构的总质量优化。罗阳军等[10]提出了一种非概率可靠性指标的迭代算法,利用该方法求解了非概率可靠性指标,进行了桁架结构非概率可靠性拓扑优化设计。实际工程结构优化问题很复杂,往往出现刚性的非线性、多极值等特点。因此,传统算法在优化过程中,存在函数求导不容易或不能求导的情况。近年来,由于群体智能优化算法,如粒子群优化(PSO)算法、差分进化(DE)算法等,具有全局搜索能力、建模简单、实现容易、收敛速度快等优点,广泛应用于解决传统的数学方法无法求解的不可微的、不连续的等复杂全局优化问题,例如基于PSO算法和混合PSO算法的结构优化设计及结构可靠性优化设计方法等[11]。PSO算法建模简单、收敛速度很快、实现容易,该算法的缺点是易发生早熟现象[12]。结构非概率可靠性优化设计为一个嵌套循环问题,外层优化结构的目标函数,同时满足给定的非概率可靠性指标要求,内层优化进行可靠性分析。为了防止PSO算法的早熟现象和提高结构非概率可靠性优化设计的精度,本文作者结合模拟退火粒子群算法(SAPSO)和差分进化(DE)算法,提出了一种基于SAPSO-DE混合算法的结构非概率可靠性优化设计方法。利用迭代算法计算结构非概率可靠性指标,建立了以结构体积最小化为目标、以非概率可靠性指标为约束条件的优化模型。算例表明,提出的SAPSO-DE混合算法有效地求解结构非概率可靠性优化问题,该设计方法能满足较高的精度要求并且可行性好。
1 SAPSO-DE混合算法
1.1 粒子群(PSO)算法
设在维空间中有N个粒子构成一个群体,第个粒子的位置和速度分别为X=(x1,x2, …,x)和V=(v1,v2, …,v)。该第个粒子经历的最佳位置为P=(p1,p2, …,p),整个粒子群经历的最佳位置为P=(p1,p2, …,p)。
粒子在解空间中通过迭代过程找到全局最优 解。在每一次迭代中,每个粒子按下式更新其速度和位置[12];

1.2 SAPSO-DE混合算法
模拟退火粒子群(SAPSO)算法[13−14]是一种基于模拟退火算法思想的算法,该算法一定程度上提高了原本PSO算法的收敛性能,但此算法属于PSO算法的变种,因此还存在早熟和局部收敛现象。为了避免这些现象,应该在搜索过程中保持种群的多样性。本文将模拟退火过程引入带压缩因子的粒子群优化算法中,构成改进模拟退火粒子群(SAPSO)算法,然后将SAPSO算法与差分进化(DE)算法相结合,提出一种SAPSO-DE混合算法。DE算法是一种基于群体的随机搜索算法,结构很简单、实现容易、稳定且全局最优解搜索能力较强,具体的内容和步骤见文献[15]。
对于规模较大的问题,2种智能优化算法的盲目结合会导致计算量巨大。本文采用基于认知经验(个体最佳位置P)进化的结合方法,也就是说,完成每代SAPSO算法后,只对认知经验改善了的个体使用一步DE算法。具体地,SAPSO算法使个体(粒子)的最佳位置分布在最小值的附近,为了提高进化过程的效果及收敛性,利用DE算法来进化认知经验(个体最佳位置P)。使用DE算法从个体最佳位置的集合中挑出一些个体。DE算法的3个操作(变异、交叉、选择)只对较好的个体最佳位置适用。这些个体最佳位置就是在SAPSO阶段内已改善的个体最佳位置。仅对认知经验发生变化(即改善)的个体应用DE算法以提高种群的多样性,以免混合算法陷入局部极点。
本文提出的SAPSO-DE混合算法的步骤如下。
1) 对种群粒子的位置X和速度V进行随机初始化。
2) 评价各粒子的适应度,将当前各粒子的位置和适应度存储在各粒子的中,将所有个体的最佳位置中适应度最优个体的位置和适应度存储于中。
3) 确定初始温度0,最终温度T,初始化退火温度T。初温方式如下[16]
7) 按下式进行退温度操作:
8) 若满足约束条件,则转步骤9),否则转步骤4)。
10) 若满足终止条件,则搜索停止,输出结果,否则转步骤2)。
2 凸模型及非概率可靠性指标
其中:为凸集合的特征矩阵,为对称正定矩阵;为正实数。设为由的特征值组成的对角矩阵,为由对应的正交化特征向量组成的矩阵,引入向量
将式(7)代入式(6),则原凸集合转换为标准化空间的单位超球集合,为
式中:为有界不确定向量的标准化向量。

图1 非概率可靠性指标的定义
求解结构非概率可靠性指标的公式如下[11]:
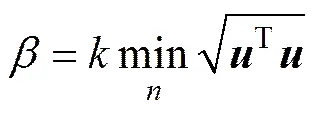
其中:
3 基于SAPSO-DE混合算法的结构非概率可靠性优化设计方法
3.1 结构非概率可靠性优化模型
在不确定参量和设计变量的约束下,对结构的非概率可靠性优化问题,可以建立如下优化模型[11]

式中:()为结构体积;为设计变量;L和U为计变量的下、上限;为不确定性参数向量;为第个约束函数的非概率可靠性指标;为第个约束函数可接受的非概率可靠性指标的最小值;为功能函数或者极限状态函数。
式(11)的优化模型为一个嵌套的优化问题,为外层优化结构的目标函数,用于对内层优化进行非概率可靠性分析。为了提高外层优化迭代过程的收敛速度和稳定性,本文内层优化采用迭代算法,外层优化采用SAPSO-DE混合算法,内层优化迭代公式如下[10]。
3.2 基于SAPSO-DE混合算法的结构非概率可靠性优化流程
基于SAPSO-DE混合算法的结构非概率可靠性优化方法流程图如图2所示。具体优化步骤如下:
1) 设定参数与建立优化模型,对种群中的每个粒子和它的最佳个体位置进行随机初始化。
3) 确立结构的极限状态方程,建立不确定参数变化范围−凸集合。将凸集合和极限状态方程分别转化为标准化空间的单位超球集合和。
4) 用迭代算法计算结构非概率可靠性指标,当满足约束条件时,停止迭代,输出值。
5) 评价各个粒子是否满足约束条件。对于满足约束条件的粒子进行模拟退火,否则转步骤10)。
6) 确定初始和最终温度,初始化退火温度。计算接受概率(T)和各个的适应度。
7) 若满足约束条件,则用式(1)和(2)更新粒子的速度和位置,否则转回步骤6)。
10) 进行退温度操作。
11) 若满足约束条件,则转步骤12),否则转步骤4)。
15) 若试验向量不满足约束条件,则重新进行变异和交叉操作。
17) 若满足终止条件,则搜索停止,输出结果,否则,转步骤4)。

图2 基于SAPSO-DE混合算法的非概率可靠性优化流程图
4 算例分析
4.1 算例1
对于多峰函数的典型例子的如下优化问题,分别采用遗传算法(GA),PSO算法和SAPSO-DE混合算法进行优化计算。
上述多峰函数有6个局部最优解,在点(−0.089 8, 0.712 6)和(0.089 8, −0.712 6)处全局最优解为 −1.031 6。该全局最优解附近的非线性程度非常高,而其他局部最优解附近的非线性程度也很高。表1所示为多峰函数的计算结果。
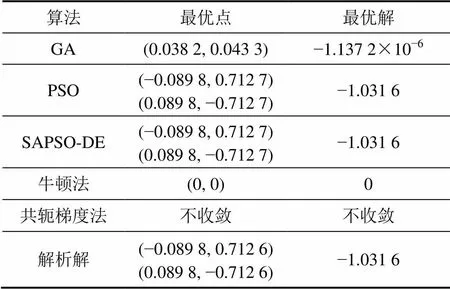
表1 多峰函数的优化结果
从表1可以看出:基于牛顿法和梯度法的优化算法在局部最优解附近处发生早熟现象,但PSO算法和SAPSO-DE混合算法收敛于解析解,两者的计算结果一致。
4.2 算例2
在结构非概率可靠性优化问题中常常利用的某10杆斜桁架如图3所示[8, 10],在节点2和3处受向不确定载荷1和2的作用,名义值皆为10 kN,变化范围用椭圆模型描述为

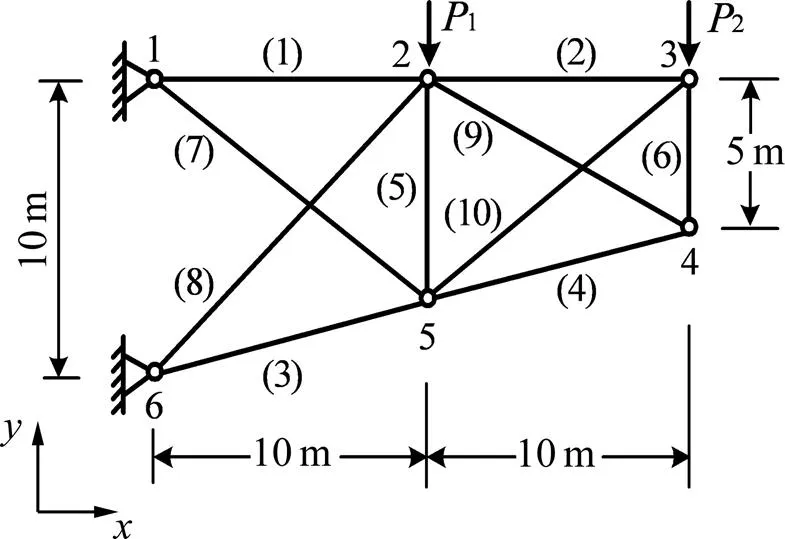
图3 (1)~(10)为杆件号
杆件1~6的弹性模量为1=200 GPa,杆件7~10的弹性模量为2=220 GPa。结构的功能函数要求节点2和3的向位移的均方根不超过0.5 mm,即

式中:2和3分别表示节点2和3的向位移。初期各杆件截面积均取2×10−2m2,设计变量的下限A=0.65×10−4m2,上限A=2×10−2m2。
该混合算法中,取粒子数N为80,PSO算法的压缩因子,认知因子,社会因子,DE算法的变异算子=0.5,交叉算子C=0.9,温度冷却系数,最大迭代次数为200,问题维数为10。
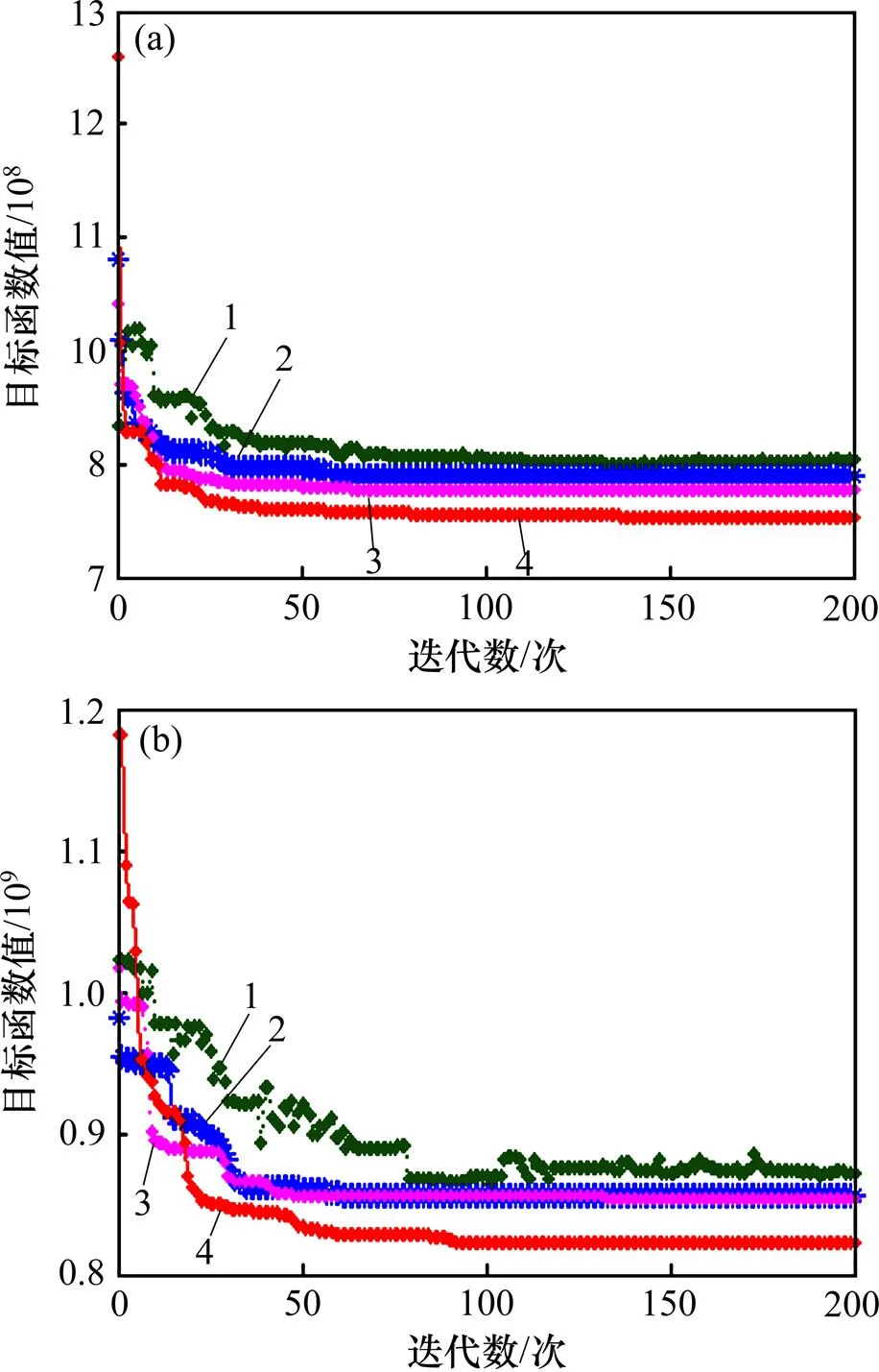
: (a) 1.0; (b) 1.5
表2和表3所示为当和时,10杆斜桁架非概率可靠性优化设计的计算结果的对比。
2.2.2 混播比例对混播植物POD活性的影响 B1和B2处理禾草POD活性极显著(P<0.01)高于B3和B4
表2 10杆斜桁架结构优化结果比较()
Table 2 Results of 10-bar slope truss structural optimization()
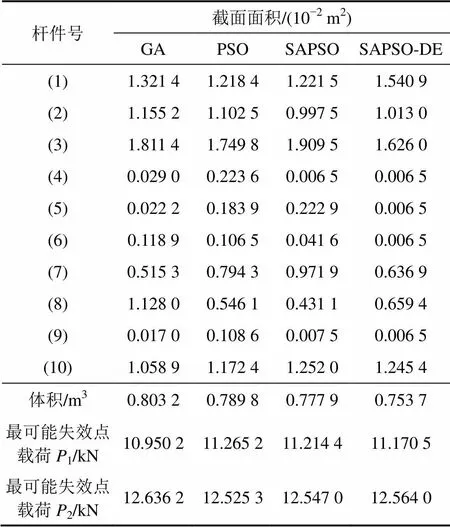
表2和表3所示为当和时,10杆斜桁架非概率可靠性优化设计的计算结果的对比。
杆件号截面面积/(10−2 m2) GAPSOSAPSOSAPSO-DE (1)1.321 41.218 41.221 51.540 9 (2)1.155 21.102 50.997 51.013 0 (3)1.811 41.749 81.909 51.626 0 (4)0.029 00.223 60.006 50.006 5 (5)0.022 20.183 90.222 90.006 5 (6)0.118 90.106 50.041 60.006 5 (7)0.515 30.794 30.971 90.636 9 (8)1.128 00.546 10.431 10.659 4 (9)0.017 00.108 60.007 50.006 5 (10)1.058 91.172 41.252 01.245 4 体积/m30.803 20.789 80.777 90.753 7 最可能失效点载荷P1/kN10.950 211.265 211.214 411.170 5 最可能失效点载荷P2/kN12.636 212.525 312.547 012.564 0
表3 10杆斜桁架结构优化结果比较()
Table 3 Results of 10-bar slope truss structural optimization()

表3 10杆斜桁架结构优化结果比较()
杆件号截面面积/(10−2 m2) GAPSOSAPSOSAPSO-DE (1)2.044 91.259 81.458 71.726 0 (2)0.966 51.518 90.562 21.131 3 (3)1.356 01.168 81.702 11.777 0 (4)0.321 90.499 30.727 30.006 5 (5)0.033 70.006 50.203 30.006 5 (6)0.350 50.393 30.170 20.006 5 (7)0.565 10.448 40.653 10.643 8 (8)1.103 01.201 20.509 10.721 5 (9)0.206 20.206 10.513 40.006 5 (10)1.029 21.215 11.331 61.353 6 体积/m30.872 50.870 80.853 70.822 8 最可能失效点载荷P1/kN11.534 711.904 411.680 811.691 1 最可能失效点载荷P2/kN14.001 613.787 413.872 513.868 9
由表2可知:与文献[10]中的结果相比,SAPSO- DE混合算法的结果与文献[10]中的结果很接近,其他3种算法的误差较大。利用基于SAPSO-DE混合算法的优化方法以后的结构体积减少了0.106%。
从表3可以看出,与其他3种优化算法相比,本文的SAPSO-DE混合算法收敛于比较好的优化解。

表4 按粒子数的变化桁架结构体积优化结果
从表4可以看出:当粒子数相同时,SAPSO-DE混合算法优化结果明显优于PSO算法结果,而且SAPSO-DE混合算法粒子数N为20时的结果要优于当粒子数N为80时PSO算法的结果。因此,与PSO算法和SAPSO算法相比,该设计方法计算成本较小而且精度很高。
通过算例,验证了本文所提优化设计方法的正确性和有效性。基于SAPSO-DE混合算法的结构非概率可靠性优化设计方法收敛速度很快,设置参数少,实现容易。
5 结论
1) 将SAPSO算法和DE算法相结合,提出了一种SAPSO-DE混合优化算法,提高了混合算法的探索能力和收敛精度,克服了PSO算法的早熟现象。
2) 针对在结构非概率可靠性指标约束下最小化结构体积的优化问题,将SAPSO-DE混合算法应用到结构非概率可靠性优化设计中,建立了结构非概率可靠性优化模型,提出了一种基于SAPSO-DE混合算法的结构非概率可靠性优化设计方法。
3) 基于SAPSO-DE混合算法的结构非概率可靠性优化方法收敛速度快,收敛稳定,易于实现。该方法的优化结果比PSO算法和SAPSO算法的优化结果更优,计算成本较小,保证了较高的精度。
[1] Elishakoff I. Essay on uncertainties in elastic and viscoelastic structures: from A.M. Freudenthal’s criticisms to modern convex modeling[J]. Computers and Structures, 1995, 56(6): 871−895.
[2] Ben-Haim Y. A non-probabilistic concept of reliability[J]. Structural Safety, 1994, 14(4): 227−245.
[3] Ben-Haim Y. A non-probabilistic measure of reliability of linear systems based on expansion of convex models[J]. Structural Safety, 1995, 17(2): 91−109.
[4] Elishakoff I. Discussion on a non-probabilistic concept of reliability[J]. Structural Safety, 1995, 17(3): 195−199.
[5] Ganzerli S, Pantelides C P. Optimum structural design via convex model superposition[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 74(6): 639−647.
[6] 乔心州, 仇原鹰, 孔宪光. 一种基于椭球凸集的结构非概率可靠性模型[J]. 工程力学, 2009, 26(11): 203−208. QIAO Xinzhou, QIU Yuanying, KONG Xianguang. Anon- probabilistic model of structural reliability based on ellipsoidal convex model[J]. Journal of Engineering Mechanics, 2009, 26(11): 203−208.
[7] 乔心州, 吕震宙. 基于区间模型的结构非概率可靠性优化[J]. 应用力学学报, 2012, 29(6): 682−687. QIAO Xinzhou, LÜ Zhenzhou. Elastic modulus reduction method for the upper bound limit analysis of beam structures[J].Journal of Applied Mechanics, 2012, 29(6): 682−687.
[8] 曹鸿钧, 段宝岩. 基于非概率可靠性的结构优化设计研究[J]. 应用力学学报, 2005, 22(3): 381−385. CAO Hongjun, DUAN Baoyan. Approach to optimization of uncertain structures based on non-probabilistic reliability[J]. Journal of Applied Mechanics, 2005, 22(3): 381−385.
[9] 王晓军, 杨海峰, 邱志平, 等. 基于非概率集合可靠性的结构优化设计[J]. 计算力学学报, 2011, 28(6): 827−832. WANG Xiaojun, YANG Haifeng, QIU Zhiping, et al. Structural optimization design based on non-probabilistic set-theoretic reliability[J]. Journal of Computational Mechanics, 2011, 28(6): 827−832.
[10] 罗阳军, 亢战. 超椭球模型下结构非概率可靠性指标的迭代算法[J]. 计算力学学报, 2008, 25(6): 747−752. LUO Yangjun, KANG Zhan. An iteration approach for structural non-probabilistic reliability analysis based on hyper-ellipsoidal models[J]. Journal of Computational Mechanics, 2008, 25(6): 747−752.
[11] 郑严, 程文明, 程跃, 等. 粒子群算法在结构非概率可靠性优化中的应用[J]. 西南交通大学学报, 2011, 46(5): 847−852. ZHENG Yan, CHENG Wenming, CHENG Yue, et al. Application of particle swarm optimization to structural non- probabilistic reliability optimization[J]. Journal of Southwest Jiaotong University, 2011, 46(5): 847−852.
[12] Clerc M, Kennedy J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(1): 58−73.
[13] 高鹰, 谢胜利. 基于模拟退火的粒子群优化算法[J]. 计算机工程与应用, 2004, 40(1): 47−50. GAO Ying, XIE Shengli. Particle swarm optimization algorithms based on simulated annealing[J]. Computer Engineering and Applications, 2004, 40(1): 47−50.
[14] 王联国, 洪毅, 赵付青, 等. 一种模拟退火和粒子群混合优化算法[J]. 计算机仿真, 2008, 25(11): 179−182. WANG Lianguo, HONG Yi, ZHAO Fuqing, et al. A hybrid algorithm of simulated annealing and particle swarm optimization[J]. Computer Simulation, 2008, 25(11): 179−182.
[15] Neri F, Tirronen V. Recent advances in differential evolution: a survey and experimental analysis[J]. Artificial Intelligence Review, 2010, 33 (1): 61−106.
[16] 龚纯, 王正林. 精通MATLAB最优化计算[M]. 北京: 电子工业出版社, 2012. GONG Chun, WANG Zhenglin. The master of MATLAB optimization calculation[M]. Beijing: Publishing House of Electronics Industry, 2012.
Structural non-probabilistic reliability optimization design based on a SAPSO-DE hybrid algorithm
JONG Chanhyok1, 2, MENG Guangwei1, LI Feng1, KONG Yongsu1, KIM Kyongil3
(1. College of Mechanical Science and Engineering, Jilin University, Changchun 130025, China; 2. College of Mechanics, University of Science, Pyongyang, DPRK;3. State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130025, China)
In order to solve the non-probabilistic reliability optimization problems of the uncertain structure, a structural non-probabilistic reliability optimal design method based on the hybrid algorithm of the simulated annealing-particle swarm optimization algorithm and the differential evolution algorithm (SAPSO-DE hybrid algorithm) was proposed. Considering the constraints of the structural non-probabilistic reliability index, the optimization model was established to minimize the structural volume. In order to improve the computational accuracy and efficiency of the structural non-probabilistic reliability, a non-probabilistic reliability optimization design was carried out based on the SAPSO-DE hybrid algorithm of the cognitive experience evolution. The results show that the non-probabilistic reliability optimization design method of structure based on the SAPSO-DE hybrid algorithm overcomes the premature phenomenon of the PSO algorithm and improves the convergence speed and precision, and the global search ability of this method is strong and has strong stability.
non-probabilistic reliability index; convex model; uncertainty; particle swarm optimization algorithm; differential evolution algorithm; simulated annealing
10.11817/j.issn.1672-7207.2015.05.009
TB114.3;TB21
A
1672−7207(2015)05−1628−07
2014−10−22;
2014−12−12
国家自然科学基金资助项目(51305157);吉林省科技厅基金资助项目(201205011, 201215048) (Project (51305157) supported by the National Natural Science Foundation of China; Projects(201205011, 201215048) supported by Science and Technology Bureau Foundation of Jilin Province)
李锋,博士,副教授,从事疲劳与结构可靠性优化设计研究;E-mail: fengli@jlu.edu.cn
(编辑 赵俊)
