基于磁传感器阵列的电磁辐射体辐射磁矩测量

2015-10-13陆志宏

舰船电子对抗 2015年6期

亓亮，陆志宏，李迪

（中国船舶重工集团公司第723研究所，扬州225001）

0 引言

对于主动式电磁探测系统，常用辐射磁矩来衡量其发射性能，进一步可以估计其作用距离。当发射天线是谐变磁偶极子天线时，其辐射磁矩的基本测量原理和测量方法是利用单个线圈在一定距离处感应的磁场值转换成电压信号进行换算。但在实际测量中，由于电磁干扰、辐射场分布的非均匀性以及测量坐标难以准确确定等因素影响，利用单个线圈测量磁矩存在较大误差，并且对距离的依赖程度很大。海工的任志良等人提出了一种基于三维场的辐射磁矩测量方法［1］，通过在场源径向方向上布放2个磁传感器测量磁场值，进而求出辐射磁矩。该方法在一定程度上提高了测量精度，但是，依然存在需要准确确定测量坐标的问题，对磁传感器的坐标一致性要求较高，而且只能在场源径向上进行测量。

本文在三维场测量辐射磁矩的基础上，通过使用磁传感器阵列来测量场源在空间不同点处的磁场值，在磁传感器坐标已知的情况下，可以计算出场源辐射磁矩，实现辐射磁矩的准确测量。使用磁传感器阵列来测量场源辐射磁矩［2］，能够获得更多的场源信息，理论上可以在场源的任意方向上测量其辐射磁矩，大大提高测量精度，对操作人员要求较低，可以很方便地实现自动化测量。

1 磁矩测量的数学模型

当源点到场点的距离远大于辐射体的尺寸时，可将辐射体近似看成是磁偶极子，进而根据磁偶极子模型可以计算空间－场点的磁场强度。将辐射体近似看做一点，设其坐标为（x0，y0，z0），其辐射的磁偶极矩m 为（mx，my，mz），场点p的坐标为（x，y，z），源点到场点的矢径为r，m与z轴正方向的夹角为θ，m在xoy平面上的投影与x轴正方向的夹角为φ，如图1所示。设辐射体辐射磁偶极矩为m，则 mx＝ msinθcosφ，my＝ msinθsinφ，mz＝mcosθ。根据磁偶极子模型，场点p处的磁场强度的矢量表达式为：

通过对空间多个已知坐标点的磁场强度的检测，就能通过式（1）建立方程组，进而求解出辐射体的辐射磁矩［3］。

2 磁矩测量系统设计

辐射体磁矩测量系统组成如图2所示，主要由磁传感器阵列、NI9239数据采集系统和磁矩测量系统软件组成。

2.1 磁传感器阵列及坐标系的建立

磁传感器使用西安华舜公司研制的HS－MSF－3－B三轴磁通门磁传感器。其测量范围为±100mOe，噪声水平低于15pT＠2Hz，带宽为0.5～4 000Hz，可以同时测量三轴磁场强度。

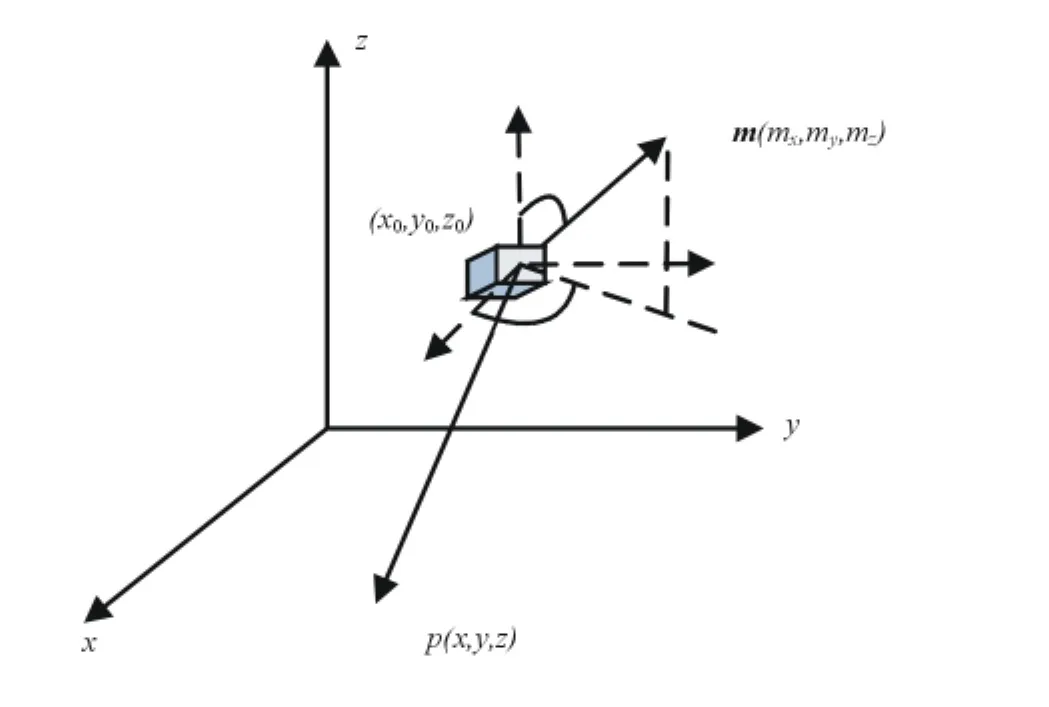
图1 辐射体空间位置和辐射磁矩方向定义

图2 磁矩测量系统组成

理论上，增加磁传感器的数目可以提高测量精度，但是同时也会增加系统复杂度和算法运算量，综合考虑，最后确定了6个测点的磁传感器排列方式，如图3所示。图中6个磁传感器在同一平面内，相邻2个磁传感器间距为0.5m，因为仿真结果表明，当磁传感器间距小于0.5m时，解算结果随着磁传感器间距的减小而增加；而当磁传感器间距大于0.5m时，会使得磁传感器阵列尺寸较大，不方便实际中的使用。制作的磁传感器阵列实物如图3所示。

图3 磁传感器阵列

在图3中，磁传感器的编号由左上角至右下角依次为1、2、3、4、5、6，以1号磁传感器作为坐标原点（0，0，0）建立如图4所示的坐标系。

因此得到1～6号磁传感器的坐标分别为（0，0，0）、（0.5，0，0）、（1，0，0）、（0，0，0.5）、（0.5，0，0.5）、（1，0，0.5），坐标单位为 m。

2.2 基于NI9239的数据采集系统

数据采集卡使用的是美国国家仪器公司的NI USB－9239模拟输入模块，该模块包括4路同步采样的模拟输入通道，每通道是24位的模数转换器。采集卡将磁传感器输入的模拟电压信号转换成数字信号，通过USB线可以实现与计算机的通信，将数据上传到计算机供测量系统软件处理分析。由于需要对6个三轴磁传感器共18个通道同时进行采样，因此共使用了5块NI USB－9239数据采集卡。

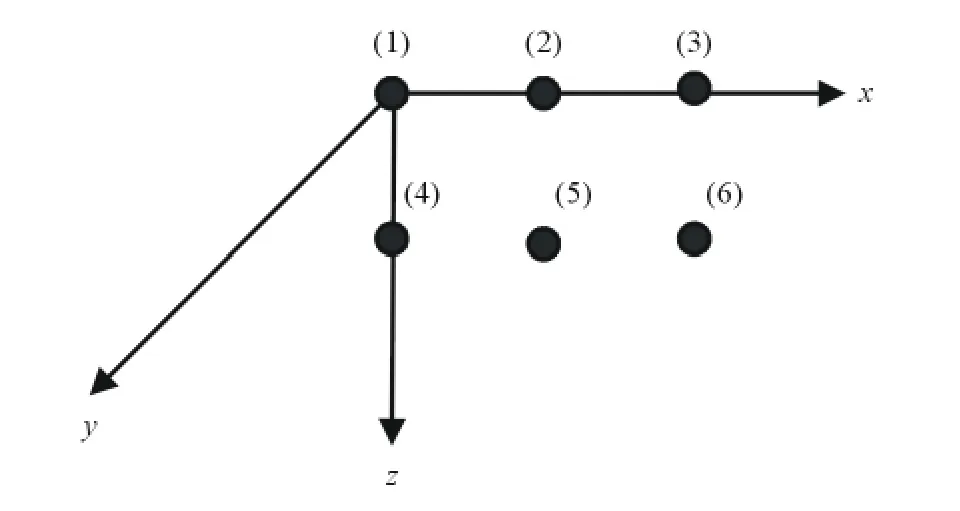
图4 磁矩测量系统坐标系

系统软件使用LabVIEW编程实现［4］，结合NI的数据采集卡可以很快捷地搭建起测试程序，通过调用LabVIEW中的MathScript节点方便地在LabView中进行文本编程。系统软件主要包含数据采集、数据处理、结果显示和数据存储等功能。采集到数据之后，根据发射信号的频率对数据进行滤波，滤波完成后，使用LabVIEW中“提取单频信息”函数得到信号的幅值等信息，再调用 Math－Script节点中编写的高斯牛顿迭代算法解算非线性方程组，得到磁矩值、辐射源位置和方位等信息，最终将结果显示出来并存储。

2.3 解算算法

将式（1）中的磁场强度H在空间直角坐标系中沿3个坐标轴进行分解，得到下式：

则根据6个磁传感器所采集到的数据可以得到18个非线性方程，组成一个超定的非线性方程组。求解非线性方程组的方法有很多，如共轭梯度法、高斯牛顿法、单纯形法、遗传算法等，这些算法各有优缺点，如单纯形法不需要计算目标函数的梯度，但是收敛速度较慢，而且是局部收敛的；而基于梯度的算法通常收敛较快，但也是局部收敛的；模拟退火法、遗传算法是全局收敛的，但是收敛速度相对较慢［5］。经过大量的仿真和实验，综合考虑收敛速度和结果精度，最后选择了高斯牛顿法作为系统的解算算法。仿真结果表明，在磁传感器间距为0.5m的条件下，代入适当的初始值，结果总能收敛到真实值，且收敛速度较快，一次求解所需要的时间在2ms以内。

3 实验研究

为了对磁矩测量系统进行测试，自行绕制了一个无铁芯线圈。骨架采用的是圆柱形空心聚氯乙烯塑料管，塑料管的直径为79mm，长度为0.5m；所使用的漆包线的直径为1.8mm，允许通过的最大电流为7.7A，共绕了247匝，根据磁矩理论计算公式，当通电电流为1A时，其产生的磁矩M＝ISW＝1×0.039 5×0.039 5×3.14×247＝1.21（Am2）。自行绕制的辐射棒如图5所示。

图5 辐射棒实物展示

3.1 辐射棒和磁传感器阵列间距对测试结果的影响

当磁传感器阵列和辐射棒间距远大于辐射棒的尺寸时，可以将辐射棒当做磁偶极子看待，进而根据磁偶极子模型来求解；但是，当二者间距太大时，会大大降低磁传感器接收到信号的信噪比，不利于分析处理数据。为了确定二者之间的最佳位置，保持发射电流1.0A不变，辐射棒和磁传感器阵列的X轴间距保持1.0m不变，Z轴间距保持0.4m不变（4号磁传感器距离辐射棒中心0.4 m），Y轴间距在3.0～7.5m范围内变化，为了减小随机误差，使测量结果更加准确，在每一个距离下采集了10次磁场数据，将10次磁场数据的均值作为最终结果进行结算磁矩，测试结果如图6所示。

从图6可以看出，当辐射棒和磁传感器阵列Y轴之间的距离为4.5m或者大于6.3m时，测量结果和理论值偏差较大，且有增大的趋势。这是因为当距离太近时，辐射棒不能够当作磁偶极子来看待，因此基于磁偶极子模型来求解也就会产生很大的误差，此时应该使用其他更为精确的模型来进行求解，但这并不是论文研究的重点；当距离太远时，磁偶极子模型成立，但是此时采集的数据的信噪比较低，因此求解结果误差也较大。

图6 发射电流一定时，不同距离下磁矩测量结果

3.2 测试系统的线性度测试

为了测量测试系统的线性度［6］，保持辐射棒的坐标位置为（2.0，4.8，0.4）m，发射电流在0.6～1.6A范围内变化，测试结果如图7所示。

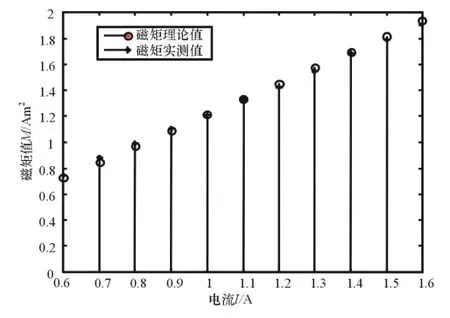
图7 间距一定时，不同发射电流下磁矩测量结果

同样从图7可以看出，实测结果和理论值吻合得很好，使用Matlab中的polyfit函数对测量数据做最小二乘拟合，得到非线性误差优于0.93%。

3.3 测量位置对测试结果的影响

为了研究辐射棒相对于磁传感器阵列的位置对磁矩测试结果的影响，分别将辐射棒放置在（3.6，3.8，0.4）、（3.6，－3.8，0.4）、（－3.6，－3.8，0.4）、（－3.6，3.8，0.4）4个位置进行测试，发射电流保持1.0A不变，同样在每个位置测试10次，对10次结果取平均，测试结果如表1所示。