回转窑传动系统的扭振计算
2015-10-12张海平
陶 瑛 张海平
中材建设有限公司(100176)
回转窑传动系统的扭振计算
陶瑛张海平
中材建设有限公司(100176)
通过建立回转窑传动系统扭转振动的数学模型及动力学模型,求出传动系统的固有频率,为回转窑传动系统的安全稳定运行提供一定的理论依据。
回转窑;传动系统;扭转振动
0 前言
在建材工业中,用回转窑煅烧水泥熟料。回转窑的技术性能和运转状况决定了水泥的质量、产量和成本,因此是水泥生产中的关键设备之一。回转窑的传动系统是:电动机、三级减速机、回转窑齿轮传动、回转窑。回转窑运行时当其激励频率与回转窑传动系统的任一固有频率相等或接近时,就会产生共振。共振时出现强烈扭转振动(除非同时有强大的阻尼或摩擦),造成机械中重要零部件的损坏。随着回转窑的大型化,设备运转的可靠性愈来愈重要。因为因机械事故造成的停车会带来极大的经济损失。
1 传动系统的数学模型
多级齿轮传动工作时,一般产生周向振动(即扭转振动)、径向振动和轴向振动。多级齿轮传动系统具有复杂性,如果同时把齿轮的径向振动和轴向振动一起考虑到系统振动模型中去,则振动模型将非常复杂,振动系统的自由度将大大增加,这给求解系统的动态响应带来困难。根据日本学者会田俊夫等的研究,齿轮的径向振动、轴向振动与扭转振动具有相同的基本频率,且三者的加速度波形相似,其振幅成一定的比例关系,基本上可以认为,径向和轴向振动是以扭转振动为激振力而产生的振动。在这三种振动中,扭转振动是系统的主要振动。为了简化问题,对于多级齿轮传动的振动系统,可以仅考虑系统的无阻尼扭转振动,这也满足工程上实际的技术要求。
回转窑的传动系统示意图见图1。
为了计算方便,把轴的转动惯量按功能等效原理,分配到各轴的齿轮或转子上,经换算,可得该系统的动力学模型,如图2所示。

图1 回转窑传动系统示意图
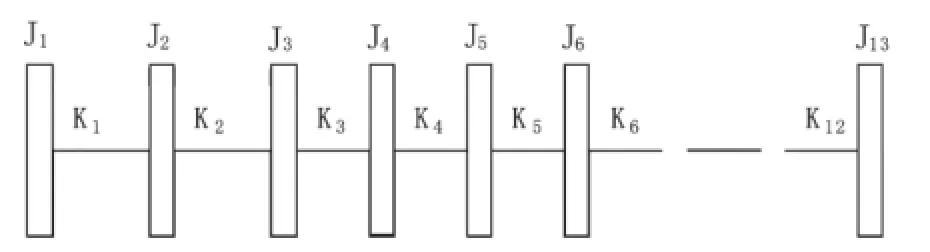
图2 回转窑传动系统的动力学模型
其中,J1——电动机转子的等效转动惯量;
J2——连接电动机端的联轴器部分的等效转动惯量;
J3——连接减速机端的联轴器部分的等效转动惯量;
J4——减速机第一级小齿轮的等效转动惯量;
J5——减速机第一级大齿轮的等效转动惯量;
J6——减速机第二级小齿轮的等效转动惯量;
J7——减速机第二级大齿轮的等效转动惯量;
J8——减速机第三级小齿轮的等效转动惯量;
J9——减速机第三级大齿轮的等效转动惯量;
J10——连接减速机端的膜片联轴器部分的等效转动惯量;
J11——连接回转窑小齿轮端的膜片联轴器部分的等效转动惯量;
J12——回转窑小齿轮的等效转动惯量;
J13——回转窑的等效转动惯量;
K1——电动机轴的等效扭转刚度;
K2——联轴器的等效扭转刚度;
K3——减速机输入轴的等效扭转刚度;
K4——减速机第一级齿轮的等效啮合刚度;
K5——减速机第一级传动轴的等效扭转刚度;
K6——减速机第二级齿轮的等效啮合刚度;
K7——减速机第二级转动轴的等效扭转刚度;
K8——减速机第三级齿轮的等效啮合刚度;
K9——减速机输出轴的等效扭转刚度;
K10——膜片联轴器的等效扭转刚度;
K11——回转窑小齿轮轴的等效扭转刚度;
K12——回转窑齿轮的等效啮合刚度。
2 扭转振动模型微分方程
对于多级齿轮传动系统,其无阻尼自由振动运动微分方程为:

式中,[J]为转动惯量矩阵;[K]为扭转刚度矩阵;{θ}为角位移列阵;{θ¨}为角加速度列阵。
在此方程式中,设所有的转动惯量均作简谐振动,则其解可写成如下形式:

式中,ωn和φ分别为某一个振型的固有圆频率和相位角;{θ}为某一振型的角位移的列矩阵;{θM}为相应的角位移的最大值或振幅向量。
将此解代入式(1),可得
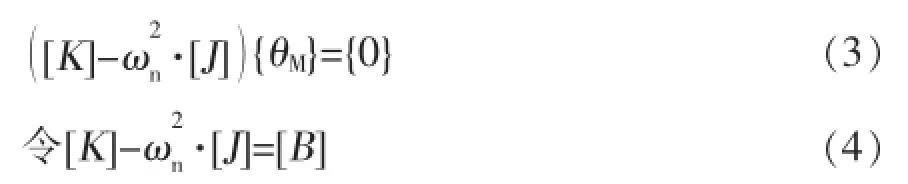
对于一个振动系统,其振幅不应全为零,即{θM}≠{0},而{θM}非零解的条件为式(4)的系数行列式应满足

式(3)称为振动系统的特征方程,式(5)为频率方程。利用式(5)可求解出固有圆频率ωn。一般情况下,若振动系统具有p个自由度,就有p个固有圆频率ω1、ω2、…ωp和对应的振幅向量}、}…{θ
由于ωp和{θM}都是振动系统的固有属性,表征着该系统的基本动态特征,所以,称{θM}为振动系统的特征向量,为特征值。每一阶固有圆频率ωni(或特征值)所对应的振幅向量,称为第i阶主振型或固有振型。
转动惯量矩阵和扭转刚度矩阵的表达式分别为:
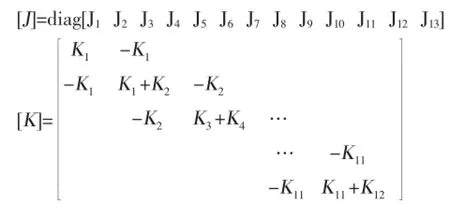
3 实例计算结果
现以公司承建项目的一实际回转窑为例进行实例计算。将各个转动惯量及扭转刚度的值代入相应的矩阵,利用Matlab软件对频率方程(5)求解出各阶固有频率和主振型,每一个固有频率有一个对应的主振型,计算结果见表1。
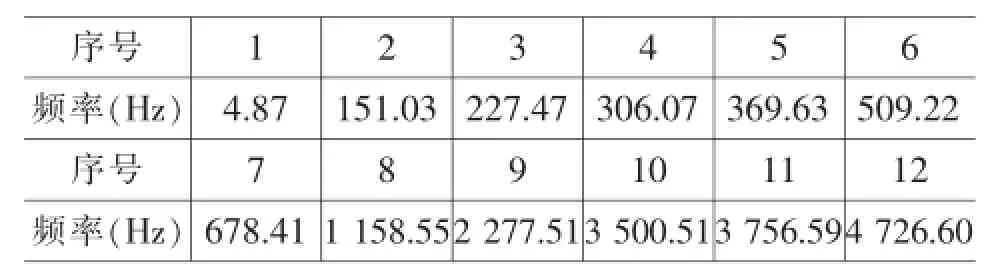
表1 固有频率
将求出的固有频率数值与传动系统的激励频率数值相比较分析,即可得出传动系统是否会发生共振。
若发现求出的系统固有频率与任一激励频率相接近,设计时,可通过调整传动系统内各转动惯量或扭转刚度的数值来改变系统的固有频率,使其远离系统的任何激励频率。

