基于颗粒离散元模型的岩石蠕变模拟试验
2015-10-11张学朋蒋宇静王刚李天斌
张学朋,蒋宇静,王刚, , 3,李天斌
基于颗粒离散元模型的岩石蠕变模拟试验
张学朋1,蒋宇静1,王刚1, 2, 3,李天斌2
(1. 山东科技大学矿山灾害预防控制省部共建国家重点实验室培育基地,山东青岛,266590;2. 成都理工大学地质灾害防治与地质环境保护国家重点实验室,四川成都,610059;3. 山东科技大学山东省土木工程防灾减灾重点实验室,山东青岛,266590)
为了从岩石颗粒之间不连续特征的角度研究其永久变形行为,基于颗粒流理论,采用颗粒离散元方法对微观颗粒之间的接触赋予Burgers模型,进行岩石二维离散元虚拟单轴蠕变试验。采用单因素法研究分析颗粒粒径、摩擦因数、颗粒法向与切向刚度比对流变特性模拟值的影响。从单轴蠕变压缩的轴向蠕变及轴向蠕变速率曲线的离散元模拟值与其解析解对比可以看出:模拟结果与解析解具有较高的吻合性;为更加明确地表示出蠕变不同阶段,选用对数蠕变柔量来进行解析解与模拟值的比对,蠕变初始阶段,PFC压缩模型会低估蠕变柔量,而在稳定蠕变阶段,两者具有高度的一致。数值模拟与解析解结果对比验证颗粒流Burgers模型适合用于岩石蠕变试验研究中,可为岩石蠕变的后续深入研究提供有益的参考。
岩石;不连续特征;永久变形;离散元法;Burgers模型
岩体的力学形态不仅表现出弹性和塑性的特征,而且具有与时间相关的流变性。由隧洞围岩变形、围岩与支护共同作用随时间的发展及岩体强度随时间的降低可看出:充分考虑岩石的流变特性,研究产生这些现象的原因及其宏细观力学机制,无论对于岩石力学理论研究,还是对于实际岩石工程应用都具有十分重要的意义。因此,国内外学者分别从室内试验、理论分析及数值模拟等方面对岩石流变力学特性展开研究。室内试验[1−4]是进行岩石蠕变特性研究的一个重要手段,但是蠕变试验因周期长、工作量大、需要消耗较大的人力和物力,从而限制了这一方法的进一步应用。利用流变理论[5−7],可进行各种复杂黏弹性、黏塑性、黏弹塑性问题的求解,而所建立的蠕变特性方程中通常含有较多不易测定的参数,这使得理论分析的应用受到较大的限制。随着计算机技术的发展,数值模拟已经与理论分析和室内试验一起成为科学研究的三大支柱。针对岩石流变特性的研究,数值模拟能够真实地模拟受施工过程等各种工程因素影响的岩体流变力学行为,已经成为一种有效的研究手段。主要方法有有限元、边界元、有限差分等[8−11]。上述模拟方法主要从岩石应力、应变状态随时间而持续增长变化的角度来进行研究,但是岩石流变特性是由于岩石矿物组构(骨架)随时间的不断调整造成的[12],而上述方法无法从细观角度揭示岩石流变的产生机理。随着岩体工程问题的日趋复杂,仅靠对表象规律性的了解已不能较好地解决复杂的工程问题,只有对岩石流变的宏细观机制进行充分研究,才有可能较好地解决这些工程问题。因此,本文作者基于颗粒流理论,采用颗粒离散元法对微观颗粒之间的接触赋予Burgers模型,进行了岩石二维离散元虚拟单轴蠕变试验,与Burgers模型理论解对比分析,用来验证此方法的可靠性,使得从细观角度研究岩石在各种影响因素下蠕变过程中内部结构的变化和改组成为可能。
1 微观接触模型及其参数确定
1.1 微观接触模型
PFC(particle flow code)中的基本模型有接触模型、滑动模型和接触黏结模型3种,在基本的岩石常规试验模拟中,常常选用接触模型和接触黏结模型来表征岩石颗粒的刚度及颗粒之间的胶结物[13],而上述模型无法描述岩石的流变特性,因此选用流变模型,本文选用PFC自带的Burgers流变模型,其基本原理如图1所示。图中:mn,ms,kn和ks为黏壶单元的黏性系数;mn,ms,kn和ks为弹簧单元的刚度系数。考虑到岩石颗粒刚度特性,同时使用接触模型中的线性接触模型。
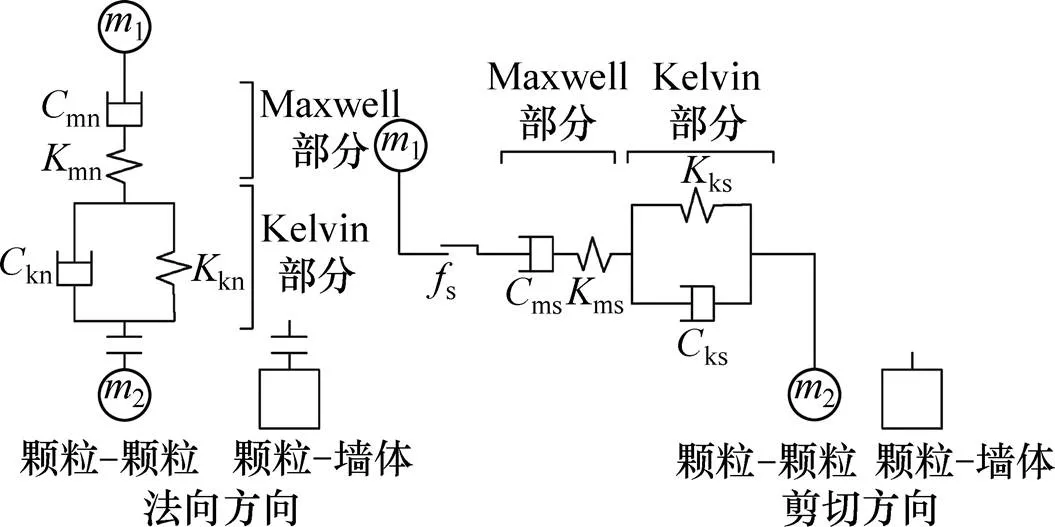
图1 Burgers模型
使用上述2种接触模型的颗粒之间是通过弹簧单元与burgers模型串联而成的,如图2所示。因此在计算过程中可以将弹簧单元与Burgers模型中弹簧原件按照弹簧串联理论进行参数校核。

图2 线性接触模型与Burgers模型并存时参数转换
1.2 宏细观参数转化
细观参数是接触点处力学性质的抽象表述,也是PFC中模型参数的间接表达。PFC中的微观模型的参数很难直接从室内试验得到,需要建立微观模型参数与宏观试验参数之间的关系,通过室内试验得到宏观试验参数,进而根据已建立的转化关系得到微观模型参数[14]。
Burgers模型本构方程如下:
式中:n和s分别为接触点处法向和切向接触力;n和s分别为接触点处法向和切向相对位移;k和k分别为开尔文单元中的法向和切向位移;mk和mk分别为麦克斯韦尔模型中弹簧单元部分的法向和切向位移;mc和mc分别为麦克斯韦尔模型中黏壶单元部分的法向和切向位移。
有研究认为[15]颗粒之间的接触特性与梁的两端连接2个颗粒的作用特性相同,因此,对于本文中所研究的颗粒之间的黏弹性特性,选用两端作用一定力和力矩的黏弹性梁来描述离散单元之间的接触特性,从而推导出黏弹性参数与细观参数之间的关系,基本原理图如图3所示。

图3 黏弹性梁示意图
在轴向加载条件下,Burgers模型3个部分位移可以通过相关的应变表示:
将式(5)代入式(1)得到法向接触力与应变之间关系:
宏观Burgers模型相应的应力表达为
式中:为黏弹性梁的长度,即相邻单元的球心距;1和1分别为Maxwell模型中弹簧单元模量与黏壶单元黏度;2和2分别为Kelvin模型中弹簧单元模量与黏壶单元黏度。
在二维情况下,假设颗粒单元的厚度为,此时黏弹性梁的厚度也为,即梁截面面积为=[15]。
由法向应力与合力关系f=得到:
将式(6)和式(7)代入式(8):
即有:
同理:
通过上述等式,即可将Burgers模型参数转换为PFC接触模型的4个法向细观参数。根据弹性模量()与剪切模量之间的关系):=2(1+)可得到PFC接触模型的4个切向细观参数[14]:
本文流变参数借鉴已有的室内压缩蠕变试验拟合参数:1=0.256GPa,2=0.470GPa,1=2100.000GPa·h,2=3.020GPa·h[16]。
模拟试验中细观流变参数使用FISH语言通过判别每2个相邻颗粒之间的距离来进行设置。线性接触模型中接触模量选取30GPa,泊松比选为0.25,线性接触模型刚度取值按照已有经验公式进行确定[17]。
1.3 时间转换
颗粒流理论是一种中心差分算法,其时步计算的理论基础是求解单自由度有阻尼弹性体系的中心差分格式下的临界时步。计算公式为:(式中:p为颗粒质量,为接触刚度)。只有在时步不超过与最小固有周期相关的极限时步时才能够保证计算结果的稳定性,且Cundall等[18]指出离散元的一个基本思想就是时步必须足够小以保证在一个时间步内扰动只会影响最近的基本单元。经过反复测试,选取固定计算时步为1.0×10−5,足以满足计算结果的稳定性及有效性。
2 蠕变压缩试验数值模型及参数研究
2.1 蠕变压缩试验数值模型建立
本研究基于BPM(bonded-particle model method)方法建立数值模型,模型尺寸采用与室内试验同样尺寸50mm×100mm(直径×高)。图4所示为颗粒平均粒径为0.3375 mm时的压缩模型。模型采用刚性wall边界(1号~4号)。为与室内试验刚性加载板相一致,上下wall端面(1号,3号)刚度设置为模型颗粒刚度的10倍,而侧向wall边界(2号,4号)设置为模型平均颗粒刚度的0.1倍,从而来实现侧向的柔性条件。通过FISH语言编写伺服机制来实现对颗粒流模型施加1MPa的轴向荷载。
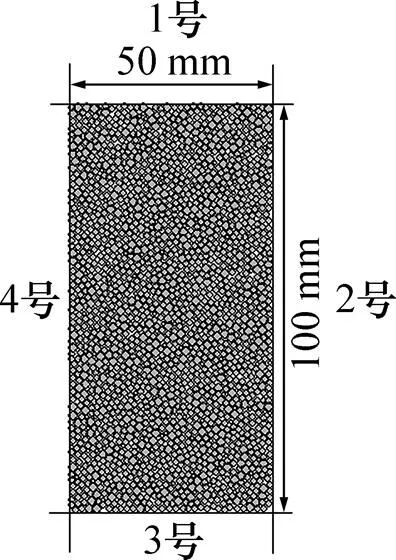
图4 蠕变压缩试验数值模型
2.2 参数研究
在PFC模拟的过程中,除了上述流变参数通过1.2节关系式确定以外,对计算结果的影响因素还有颗粒粒径、摩擦因数、颗粒法向与切向刚度比,对上述3个参数的影响研究采用单因素分析法。
2.2.1 颗粒粒径影响分析
使用不同颗粒粒径建立压缩试验模型,不同颗粒粒径时模型的颗粒总数如表1 所示。图5和图6所示分别为不同颗粒粒径下模型的轴向应变及蠕变速率曲线。从图5可以看出:随着颗粒粒径的增大,轴向应变整体上呈现出增大的趋势,在小的范围内也会存在一定的反增长趋势,如平均颗粒粒径2.2500mm下的轴向应变要小于平均颗粒粒径1.6875mm下的轴向应变;随着颗粒粒径的减小,正增长的影响程度逐渐减小。从图6可以看出:初始蠕变阶段,蠕变速率随着颗粒粒径的增加而增大,到达稳定蠕变阶段,颗粒粒径对蠕变速率几乎不产生影响;当颗粒粒径较大(如3.000~3.750mm)时,稳定蠕变阶段的蠕变速率会存在较大的起伏变化。通过轴向应变及轴向蠕变速率曲线综合比对可知:不同颗粒粒径下的压缩模型从初始蠕变到稳定蠕变过渡所经历的时间约为30h,颗粒粒径对初始蠕变阶段到稳定蠕变阶段过渡所需要的时间影响不大。

表1 影响参数的模拟工况

颗粒粒径/mm:1—3.000~3.750;2—2.000~2.500;3—1.500~1.875;4—1.000~1.250;5—0.800~1.000;6—0.500~0.625;7—0.300~0.375;8—0.200~0.250

颗粒粒径/mm:1—3.000~3.750;2—2.000~2.500;3—1.500~1.875;4—1.000~1.250;5—0.800~1.000;6—0.500~0.625;7—0.300~0.375;8—0.200~0.250
综上所述,颗粒粒径对模型轴向应变以及初始蠕变阶段的轴向蠕变速率产生一定的影响,随着颗粒粒径变小,这种影响逐渐变小,在平均颗粒粒径 0.5625~0.2250 mm范围内,轴向应变及其变化速率在很小的范围内浮动。因此考虑到模型计算效率问题,在后续的研究中选择平均颗粒粒径为0.3375mm的颗粒。
2.2.2 摩擦因数影响分析
选取0~1.0范围内的摩擦因数来分析其对模型试验的影响,具体工况如表1所示。图7和图8所示分别为不同摩擦因数下模型的轴向应变及蠕变速率曲线。从图7可以看出:瞬时蠕变随着摩擦因数的增加逐渐增大,而其影响程度随着摩擦因数的增加有所减小。初始蠕变阶段和稳定蠕变阶段,摩擦因数为0时,轴向应变最大,随着摩擦因数的增加,模型内部内聚力加大,从而使得轴向应变逐渐减小。从图8可以看出:摩擦因数对蠕变速率不产生任何影响,不同摩擦因数下的压缩模型从初始蠕变到稳定蠕变过渡所经历的时间约为30h,可以看出摩擦因数对初始蠕变阶段到稳定蠕变阶段过渡所需要的时间影响不大。

摩擦因素:1—0;2—0.2;3—0.5;4—0.6;5—0.7;6—1.0

摩擦因素:1—0;2—0.2;3—0.5;4—0.6;5—0.7;6—1.0
2.2.3 颗粒刚度比影响分析
选取0.5~5.0范围内的刚度比来分析其对模型试验的影响,具体工况如表1所示。图9和图10所示分别为不同颗粒刚度比下模型的轴向应变及蠕变速率曲线。从图9可以看出:颗粒刚度比的影响存在一个临界点,在所选取的几个工况中,当颗粒刚度比小于1.0时,轴向蠕变会随着颗粒刚度比的增加而逐渐增加,但是当颗粒刚度比超过1.0时,颗粒刚度对轴向应变几乎不产生影响。从图10可以看出:颗粒刚度比对蠕变速率不产生任何影响。通过轴向应变及轴向蠕变速率曲线综合比对可知,不同颗粒刚度比下的压缩模型从初始蠕变到稳定蠕变过渡所经历的时间约为30h,可以看出颗粒刚度比对初始蠕变阶段到稳定蠕变阶段过渡所需要的时间影响不大。
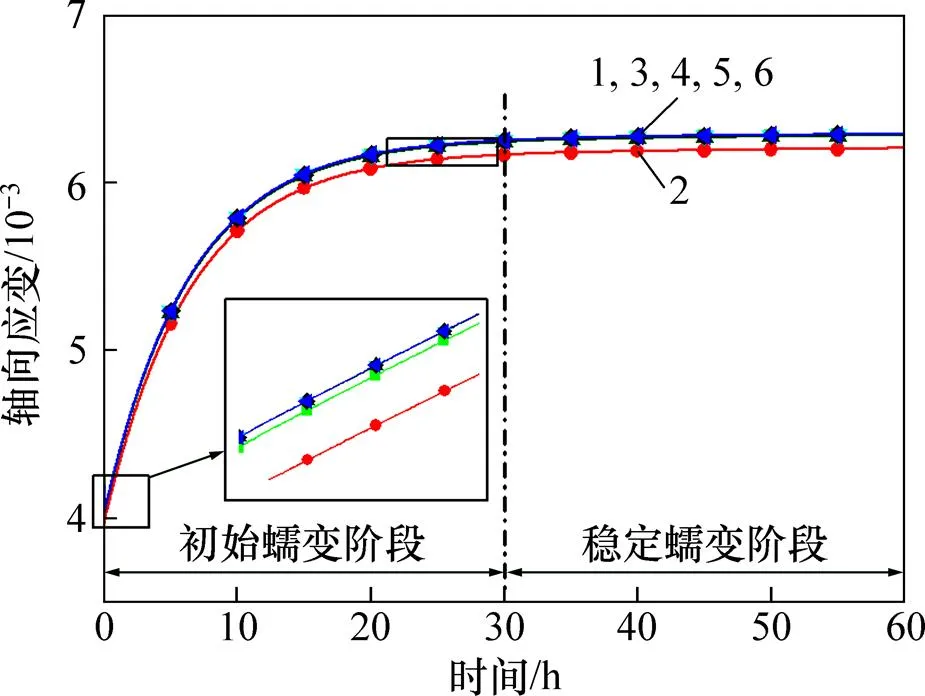
刚度比:1—0.5;2—1.0;3—2.0;4—3.0;5—4.0;6—5.0

刚度比:1—0.5;2—1.0;3—2.0;4—3.0;5—4.0;6—5.0
3 压缩蠕变数值模拟结果验证
为了验证数值模拟结果的正确性,将模型试验结果与Burgers解析解进行比对分析。
3.1 Burgers模型
宏观Burgers模型如图11所示,其一维本构方程和蠕变方程为:
式中:1和2分别为瞬时弹性模量和黏性模量;和分别为应力对时间的一次求导和二次求导;和分别为应变对时间的一次求导和二次求导;1和2为黏滞系数。
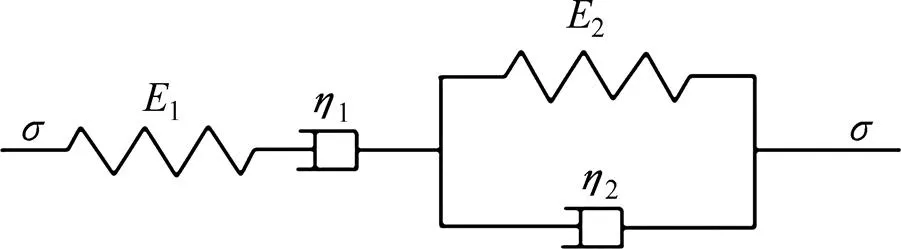
图11 Burgers模型
3.2 蠕变压缩模拟结果验证
根据上述不同参数对结果的影响分析研究,选取颗粒平均粒径为0.3375mm,摩擦因数为0.5,颗粒法向与切向刚度比为3.0,流变参数根据1.2节方法进行确定。图12~14所示为1.0MPa轴向荷载下Burgers模型的解析解与模拟值的对比。

1—Burgers解析解;2—PFC模拟值

1—Burgers解析解;2—PFC模拟值

1—Burgers解析解;2—PFC模拟值
由图12可见:两者具有较高的吻合度,但是模拟解要比解析解略大。这是由于:PFC压缩模型的内部孔隙率与实际试件内部孔隙率存在着不同,另外,本文PFC压缩模型采用圆形颗粒与真实岩石颗粒存在着差别。
从图13可以看出:解析解与模拟值具有良好的吻合度,并且从初始蠕变阶段向稳定蠕变阶段转变的时间也具有很高的吻合度。
为了更加明确地表示出蠕变不同阶段,选用对数蠕变柔量来进行解析解与模拟值的比对,如图14所示。由图14可以看出:在蠕变初始阶段,PFC压缩模型会低估蠕变柔量,而在稳定蠕变阶段,两者具有高度的一致性。
4 结论
1) 基于颗粒流理论,在解决Burgers模型宏细观参数等问题后,采用PFC程序建立单轴蠕变颗粒流模型,实现了岩石二维离散元虚拟单轴蠕变试验。
2) 确定宏细观蠕变参数以后,采用单因素法研究分析了颗粒粒径、摩擦因数、颗粒法向与切向刚度比值对流变特性的影响。颗粒粒径及刚度比对轴向蠕变的影响都存在一个临界值,超过临界值以后,轴向蠕变随着颗粒粒径的增大而增大,而不受刚度比的影响;轴向蠕变随着摩擦因数的增加出现非线性增加的趋势;初始蠕变阶段,蠕变速率随着颗粒粒径的增加而增加,而不受摩擦因数和颗粒刚度比的影响,稳定蠕变阶段,三因素对蠕变速率几乎不产生影响。
3) 单轴蠕变压缩的轴向蠕变及轴向蠕变速率曲线的离散元模拟值与其解析解具有较高的吻合性;为了更加明确地表示出蠕变不同阶段,选用对数蠕变柔量来进行解析解与模拟值的比对。在蠕变初始阶段,PFC压缩模型会低估蠕变柔量,而在稳定蠕变阶段,两者具有高度的一致。
4) 验证了颗粒流Burgers模型适合用于岩石蠕变试验研究中,使得从细观角度研究岩石在各种影响因素下蠕变过程中内部结构的变化和改组成为可能,从而通过宏细观变形机理的综合分析,能够进一步充实岩体流变理论,促进岩体流变理论的工程应用。
[1] Boukharov G N, Chanda M W, Boukharov N G. The three processes of brittle crystalline rock creep[J]. International Journal of Rock Mechanics and Mining Sciences, 1995, 32(4): 325−335.
[2] Maranini E, Brignoli M. Creep behaviour of a weak rock: Experimental characterization[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(2): 127−138.
[3] 赵旭峰, 孙钧. 海底隧道风化花岗岩流变试验研究[J]. 岩土力学, 2010, 31(2): 403−406. ZHAO Xufeng, SUN Jun. Testing study of rheological characteristics of weathered granite in undersea tunnel project[J]. Rock and Soil Mechanics, 2010, 31(2): 403−406.
[4] 蒋昱州, 徐卫亚, 王瑞红, 等. 拱坝坝肩岩石流变力学特性试验研究及其长期稳定性分析[J]. 岩石力学与工程学报, 2010, 29(增2): 3699−3709. JIANG Yuzhou, XU Weiya, WANG Ruihong, et al. Experimental study of rheological mechanical properties of Arch Dam Abutment rock and its long-term stability analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(Supp.2): 3699−3709.
[5] 佘成学, 孙辅庭. 节理岩体黏弹塑性流变破坏模型研究[J]. 岩石力学与工程学报, 2013, 32(2): 231−238. SHE Chenghe, SUN Futing. Research on Visco-elastoplastic rheological failure model of jointed rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(2): 231−238.
[6] Jin J S, Cristescu N D. An elastic viscoplastic model for transient creep of rock salt[J]. International Journal of Plasticity, 1998, 14(1/3): 85−107.
[7] 王伟, 吕军, 王海成, 等. 砂岩流变损伤模型研究及其工程应用[J]. 岩石力学与工程学报, 2012, 31(增2): 3650−3658. WANG Wei, LÜ Jun, WANG Haicheng, et al. A rheological damage model of sandstone and its application to engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(Supp 2): 3650−3658.
[8] 夏熙伦, 徐平, 丁秀丽. 岩石流变特性及高边坡稳定性流变分析[J]. 岩石力学与工程学报, 1996, 15(4): 312−322. XIA Xilun, XU Ping, DING Xiuli. Rheological characteristics of rock and stability Rheological analysis for high slope[J]. Chinese Journal of Rock Mechanics and Engineering, 1996, 15(4): 312−322.
[9] Tullis T E, Horowitz F G, Tullis J. Flow laws of multiphase aggregates from end-member flow laws[J]. Journal of Geophysical Research: Solid Earth, 1991, 96(B5): 8081−8096.
[10] Kontoni D P N, Beskos D E. Boundary element formulation for dynamic analysis of nonlinear systems[J]. Engineering Analysis, 1988, 5(3): 114−125.
[11] 褚卫江, 徐卫亚, 杨圣奇, 等. 基于FLAC3D岩石黏弹塑性流变模型的二次开发研究[J]. 岩土力学, 2006, 27(11): 2005−2010. CHU Weijiang, XU Weiya, YANG Shengqi, et al. Secondary development of a viscoelasto-plastic rheological constitutive model of rock based on FLAC3D[J]. Rock and Soil Mechanics, 2006, 27(11): 2005−2010.
[12] 孙钧. 岩石流变力学及其工程应用研究的若干进展[J]. 岩石力学与工程学报, 2007, 26(6): 1081−1106. SUN Jun. Rock rheological mechanics and its advance in engineering applications[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(6): 1081−1106.
[13] Cho N, Martin C D, Sego D C. A clumped particle model for rock[J]. International Journal of Rock Mechanics & Mining Sciences, 2007, 44(7): 997−1010.
[14] LIU Yu, DAI Qingli, YOU Zhangping. Viscoelastic model for discrete element simulation of asphalt mixtures[J]. Journal of Engineering Mechanics, 2009, 135(4): 324−333.
[15] Itasca Consulting Group Inc. Manual of particle flow code in 2-dimension (Version 3.10): Augmented fishtank[M]. Minneapolis: Itasca Consulting Group Inc, 2004: 11−12.
[16] 李星星, 任光明, 王志红, 等. 岩石单轴压缩流变参数的确定[J]. 水电能源科学, 2011, 29(8): 42−45.LI Xingxing, REN Guangming, WANG Zhihong, et al. Determination of uniaxial compression rheological parameters[J]. Water Resources and Power, 2011, 29(8): 42−45.
[17] Potyondy D O, Cundall P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics & Mining Sciences, 2004, 41(8): 1329−1367.
[18] Cundall P, Strack O. A discrete numerical model for granular assemblies[J]. Geotechnique, 1979, 29(1): 47−65.
Creep simulation test of rock based on particle discrete element method
ZHANG Xuepeng1, JIANG Yujing1, WANG Gang1, 2, 3, LI Tianbin2
(1. State Key Laboratory of Mining Disaster Prevention and Control Co-founded by Shandong Province and the Ministry of Science and Technology, Shandong University of Science and Technology, Qingdao 266590, China; 2. State Key Laboratory of Geohazard Prevention and Geoenvironment Protection, Chengdu University of Technology, Chengdu 610059, China;3. Shandong Provincial Key Laboratory of Civil Engineering Disaster Prevention and Mitigation,Shandong University of Science and Technology, Qingdao 266590, China)
In order to investigate the permanent deformation behavior of rock considering its discontinuous feature, a two-dimension (2D) virtual uniaxial creep test of rock was developed based on the particle flow theory. According to the discrete element method, the micro parameters of Burgers model in particle flow code (PFC) was studied first. The effects of the micro-properties such as the particle radius, friction coefficient and the ratio of particle normal and shear stiffness on its creep behavior were examined using the single factor method. The simulated results of the axial strain and its rate exhibit similar trends to their corresponding analytical results. The main advantage of plotting the creep compliance is that it allows easy identifying of the distinct creep stages. The comparison shows that the simulation results underestimate the creep compliance in the initial creep stage but do a satisfactory prediction in the steady-state creep stage. The correctness of Burgers model in the study of rock creep behavior was verified by the comparison between the simulation and analytical results and it can function as a beneficial reference for further research on the rock creep in PFC.
rock; discontinuous feature; permanent deformation; discrete element method; Burgers model
10.11817/j.issn.1672-7207.2015.10.047
TU452
A
1672−7207(2015)10−3914−08
2015−02−02;
2015−04−09
国家自然科学基金资助项目(51279097,51379117,51479108);山东省博士后基金资助项目(201402014)(Projects (51279097, 51379117, 51479108) supported by the National Natural Science Foundation of China; Project (201402014) supported by the Shandong Province Postdoctoral Science Foundation)
王刚,博士,副教授,从事岩石力学与工程方面研究;E-mail:wanggang1110@gmail.com
(编辑 陈爱华)
