质量密度及围压影响的堆积碎石土变形特性分析

董辉，胡自然，傅鹤林，陈铖，陈玺文



质量密度及围压影响的堆积碎石土变形特性分析

董辉1, 2，胡自然1，傅鹤林3，陈铖1，陈玺文1

(1. 湘潭大学土木工程与力学学院，湖南湘潭，411105；2. 湘潭大学流变力学研究所，湖南湘潭，411105；3. 中南大学土木工程学院，湖南长沙，410075)

考虑质量密度(不同含石量、含水率)及围压对碎石土变形特征的影响规律，对具有级配代表性的湖南昭山区某斜坡堆积碎石土进行试验研究。研究结果表明：质量密度和围压有着联合影响，堆积碎石土在不同质量密度下应力−应变曲线表现为台阶状，即应变先硬化再软化，对于7%含水率的则只出现应变软化；随着围压的增大，初始切线模量和剪切峰值都增大，但不随质量密度的变化而线性增长，屈服轨迹成平行线；在低围压下发生剪缩，高围压发生剪胀；堆积碎石土压硬性对含石量更敏感，剪胀性对含水率更敏感，存在一个最佳含水率和最佳含石量；剪胀率及有效应力比可以成为剪胀性的判断依据。同时发现不同质量密度及围压下的体应变主要集中在2条曲线之间，可以作为连续强降雨雨后滑坡失稳临界状态的一个判断依据。

滑坡；碎石土；质量密度；压硬性；剪胀性

堆积碎石土是风化卸荷、残坡积等复杂成因形成的第四纪土与石块的二重介质混合体，是介于土体与碎裂岩体之间的一种特殊地质体，作为坡体物质或滑体物质的滑坡，广泛分布于我国西南及西北地区，往往因降雨或工程活动致滑成灾造成了巨大的经济损失甚至人员伤亡。然而，因其物质组成的复杂性，结构分布的不规则性，给其工程性质与变形特性的研究带来了极大的困难。研究堆积碎石土压硬性与剪胀性是建立其本构关系的重要前提，也是进行以堆积碎石土为主体材料的实际工程应力应变分析的重要依据，因此国内外有一批学者致力于其力学及变形特性(压硬性和剪胀性)研究。20世纪以来国内外学者针对土的剪胀特性进行了很多的研究，随着科技发展、研究的深入及工程需要，将研究范围扩展到了土石混合体、堆石料等一些其他复杂性质材料，并取得了一定的研究成果。刘萌成等[1−6]进行了大量的大型三轴试验，得出很多有价值的成果，如初始物理力学状态(初始孔隙比和固结压力)是堆石料发生剪胀或剪缩的决定性因素；围压是影响堆石料强度和变形特性的最重要因素，随着围压的升高，堆石料的剪胀性会急速降低；堆石料在剪切过程中应变软化与否和剪胀性取决于该堆石料本身密度和所施加的围压，且在应变足够大时，土样出现临界状态等。随着研究方法改进和相似材料的诞生，孔德志等[7]采用人工模拟堆石料和三轴试验的方法研究了不同破碎率情况下模拟堆石料应力变形和破碎体应变的特性。Shafiee等[8−9]则从渗透率的角度对土石混合物变形特性影响规律进行了研究。这些研究成果都具有指导性意义，然而也有其局限性。绝大部分研究都是在CD试验的基础上只考虑单一因素(密度、围压、初始应力或孔隙比等)的影响，而实际工程问题往往由诸多因素联合作用，研究中也很少考虑到含石量与含水率对变形特性的影响以及最佳含量与临界状态的问题，而这两种因素的影响却是相当重要的。对于堆积碎石土这种特殊材料的变形特性研究目前不是很多，然而这种材料在工程实际中却有着举足轻重的作用。Wang等[10]基于大型直剪试验研究了碎石土应力应变关系和抗剪强度。梁燕等[11]研究了水对临河碎石土路堤的稳定性及破坏形态的影响规律。针对连续强降雨雨后残坡积(堆积)碎石土滑坡失稳破坏的灾害问题，本文作者以湖南昭山区某失稳斜坡为研究对象，对其具有级配代表性的碎石土坡体物质，以室内的三轴固结不排水试验，结合理论分析质量密度(含水率、含石量)及围压对其破坏表象、抗剪强度和变形特性(压硬性、剪胀性)及临界状态的联合影响规律，并提出临界状态的拟合方程，从而进一步掌握堆积碎石土的变形特征，为类似滑坡防治提供理论依据。

1 变形特性研究方案

1.1 不同质量密度原材料选取

为了更好地体现质量密度的影响以及研究的工程意义，原材料的选取是至关重要的。实验材料取自昭山某具有级配代表性的堆积碎石土斜坡，天然状态含石量(质量分数)为83%，含黏粒量(质量分数)为17%，含水率(质量分数)为11.4%，母岩为粉质砂岩，黏粒为红黏土。最大碎石粒径为84 mm。材料级配曲线见 图1。

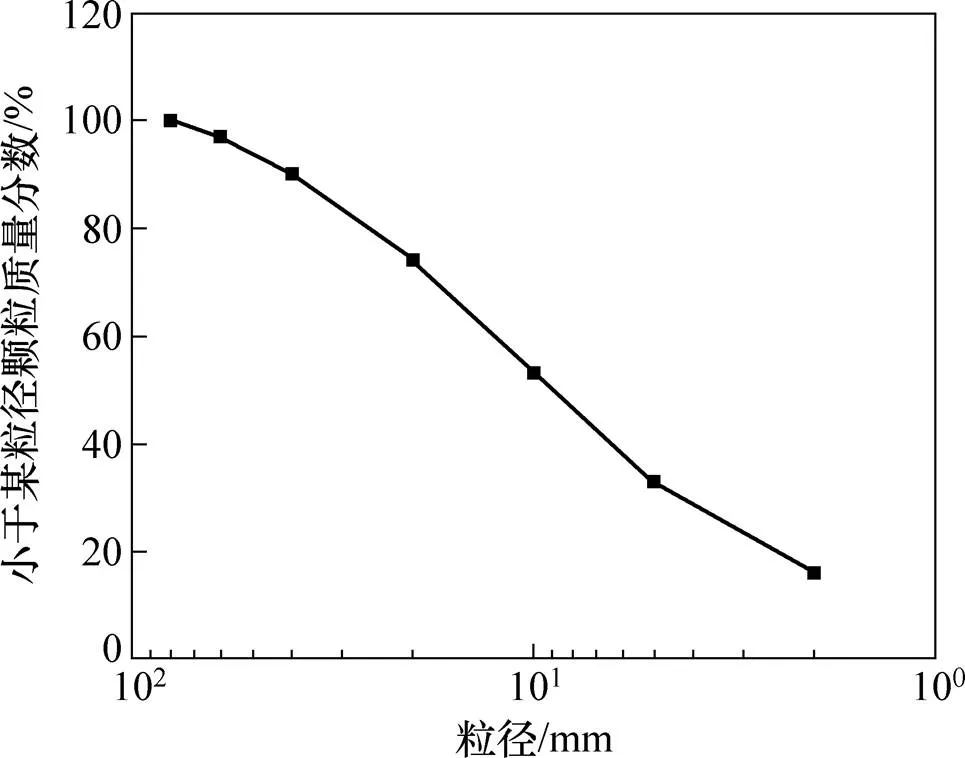
图1 碎石土颗粒组成

1.2 质量密度及围压配置

将取回的堆积碎石土烘干、过筛，根据等量替代法将碎石粒径换算成小于20 mm的粒组。本文主要从质量密度及围压2个方面研究堆积碎石土的变形特性，因此，根据质量密度将实验分成6组(含石量60%，40%和20%；含水率13%，11%，9%和7%；其中含石量为60%、含水率为11%的一组共用)，每组设定三级围压(100，200和400 kPa)，每组试样的基本物理力学性质见表1。实验采用固结不排水剪切，在设定的围压下进行各向等压饱和、固结排水，最后在各向等压下施加轴向力进行剪切。参照前人研究成果[12−13]、土工试验规程的要求、三轴仪位移限制(65 mm)条件以及考虑到堆积碎石土特有性质，采用101 mm实验,剪切速率控制为1 mm/min，轴向应变为30%时结束 实验。

表1 试样方案和基本物理性质

2 变形结果分析

2.1 破坏变形分析

岩土体的逐渐破损理论是岩土界的焦点问题之一，试样的剪切破损是一个渐变过程。图2所示为试样剪切前后形状。由图2可见：试样在轴向和径向都发生了很大变形，整个试样有明显的鼓胀如图2(b)，通过量测，围压越小鼓胀越大。试样破坏时形态为破裂带而非破裂面，与主应力成45°角，图2(b)所示的2条线之间。

(a) 剪切前；(b) 剪切后

2.2 堆积碎石土压硬性分析

压硬性是土体的变形特性之一，堆积碎石土同样具有这种变形特性，主要表现为应变硬化或应变软化。

图3所示为在不同质量密度和围压情况下的主应力差−轴向应变关系。由图3可见：1) 在含水率不变、含石量变化的情况下，随着轴向应变的增大，曲线几乎没有线性变化阶段，即试样从开始受到轴向荷载时，几乎没有弹性变形而很快进入塑性变形阶段。2) 整个应力−应变曲线有明显的台阶状(硬化增强)，这与丁秀丽等[14]研究结果一致。围压越小，台阶状越明显(图3(a)，以=20%，=11%为例)，且围压为100 kPa、含石量为20%时尤为突出(图3(b))，峰值由97.6 kPa增长到124.2 kPa，增长率达29%(含石量40%，曲线平缓；含石量60%，增长率20%)，这是由于高围压限制了试样内的碎块石的移动而不能使其发挥骨架效应。偏应力的增长并非随着含石量的增大而单调增长，含石量为40%时强度是最大的，且以最快速率达到最大承载力。在围压为100 kPa、含水率为11%时，含石量为20%，40%和60%时的台阶状偏应力增长率分别为0.27，0.06和0.19，可见偏应力最大时(40%)，增长率(0.06)并不是最大，表明土和石在40%含石量时发挥了更好的联合抗力效应，堆积碎石土存在某一最佳含石量使得其发挥最好的力学性能。3) 曲线在达到第1次剪切峰值后，残余应力保持平缓，表现为应变硬化，一段时间后曲线出现第2次剪切峰值，比第1次峰值大，为应力强化。第2次峰值后曲线有下降趋势(应变30%结束试验，不能显示全部曲线)，出现应变软化。由此可知：在轴向压力作用下，首先发生作用的是堆积碎石土中的土体和孔隙水体，强度相对较低的土体首先进入塑性状态，表现为第1个剪切峰值。达到第1次峰值后，土中的碎石块发生滚动、滑移和错位，将土体排挤开，块体和块体开始接触抵抗，导致碎石土整体强度有所提高，形成应变硬化及强化阶段，表现为第2剪切峰值。峰值过后，试样开始破坏，曲线下降。4) 在含石量不变、含水率变化的情况下，堆积碎石土应力−应变曲线的走势与压硬性变化规律与含石量变化时大体一致，均出现台阶状，应变硬化。区别在于含水率为7%时，应力应变曲线达到峰值之后，出现应变软化现象，然后才进入第2次峰值，且第2次峰值小于第1次峰值，判断含水率对碎石土的压硬性具有显著影响，且含水率低于某值(本实验为7%)时，碎石土的整体强度并不能得到提高。5) 综合不同质量密度及围压的应力−应变曲线，发现这3种影响堆积碎石土压硬性的因素存在着交叉效应，本实验含石量为60%、含水率为9%、围压为100 kPa为最优组合，充分发挥了土、水和石的联合效应，材料的应变硬化与强度都得到提高。不同含石量较不同含水率的应力−应变曲线斜率变化更大，表明碎石土的压硬性对于含石量的变化更为敏感。

(a) P=20%，w=11%不同围压应变曲线；(b) 100 kPa围压应力−应变曲线；(c) 100 kPa围压；(d) 200 kPa围压；(e) 400 kPa围压

压硬性的另一体现为初始切线弹性模量和抗剪强度随着围压的增大而增大。康纳发现，点绘(1−3)−可以用双曲线拟合，可以表示为[14]

由理论研究可知：

因此可求得初始切线模量为76.9 kPa。其他几组质量密度的结果见表2。

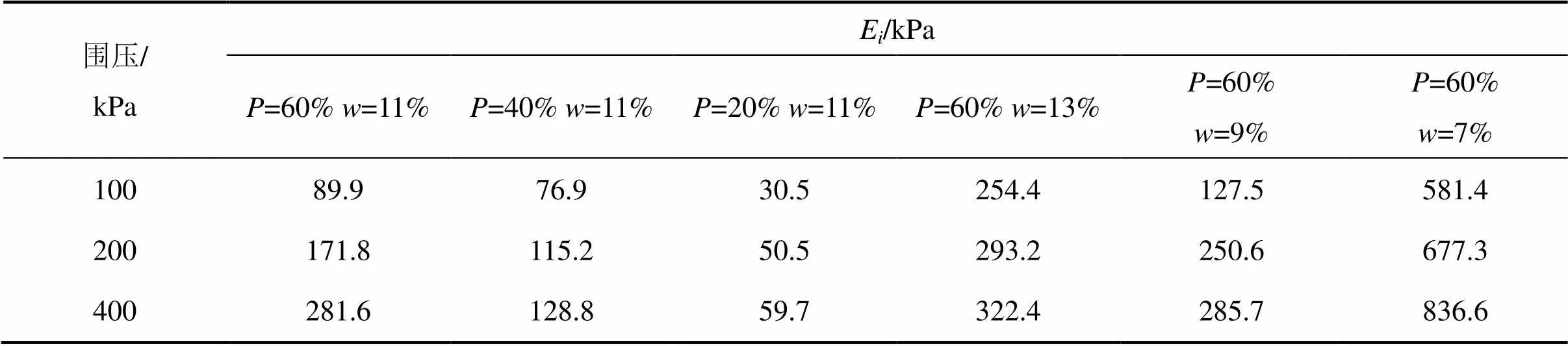
表2 初始切线模量

不同质量密度和围压下的剪切峰值见表3。

表3 剪切峰值

将不同质量密度的初始切线模量和剪切峰值绘于坐标系中(由于含石量不变、含水率变化及含水率不变、含石量变化时曲线特征相似，此处以含水率为11%为代表绘图5(a)，以含石量为60%绘图5(b))，由图5可见：1) 随着3的增大，初始切线模量和剪切峰值都增大。2) 图5(a)中，含石量变化时，相同围压下，初始切线模量不随含石量的增加而线性增长，含石量为60%时最大。3越大，含石量的影响越显著，表现为初始弹性模量增长幅度越大。3) 图5(b)中，初始切线模量与剪切强度数值跨径比图5(a)中的大，随含水率的变化也并非线性变化。含水率为7%时最大，11%时最小，与应力−应变曲线相一致。抗剪强度曲线出现交叉，说明碎石土存在一个最佳含水率使得初始切线模量与剪切峰值都为最大，从而充分发挥碎石土的力学性能。4) 分析试样在−3平面内的屈服轨迹，基本上保持平行，含石量变化时的屈服轨迹间距更大。整体上，初始切线模量和剪切峰值曲线的切线斜率并非常数，相比不同含水率，含石量不同时斜率变化更大(曲线更分散、前期紧凑、后期开口更大，如图5(a)所示，因此，堆积碎石土初始切线模量和剪切峰值对含石量的敏感程度明显强于含水率对含石量的敏感程度，这与2.2节研究结果一致。

(a) 含水率不变，含石量变化；(b) 含石量不变，含水率变化

2.3 堆积碎石土剪胀性分析

剪切过程引起体积收缩，叫剪缩；引起体积膨胀，叫剪胀。剪缩可以看成是负剪胀，因此，统称为剪 胀[16]。剪胀性也是土体的一大变形特性。

图6(a)所示为以含石量60%，含水率11%为代表研究碎石土的剪胀性。从图6(a)可见：1) 堆积碎石土在剪切过程中表现出明显的剪胀特性，在开始试验阶段，曲线变化较陡，体积变化率较大，随着轴向应变的增加，曲线趋于平缓，表明碎石土进入临界状态[17]。2) 随着围压的升高，由剪胀转变为剪缩，围压越高，剪缩越大。3) 在低围压时，碎石土首先表现出剪缩特性，随着轴向应变的增加，剪缩变成剪胀。这是由于在低围压时，碎石土在刚受到轴向剪力时，轴向应力远小于侧向应力，试样主要受侧向力的作用而体积缩小，剪缩。随着轴向应力的增大，以致超过侧向应力，试样在轴向力的作用下发生较大的变形，此时侧向力相对轴向力较小，试样整体强度不高，而发生剪切破坏，导致后段剪胀的产生。

分析100 kPa围压下，不同含水率时的剪胀特性如图6(b)所示。由图6(b)可知：1) 在低围压下，试样基本上为剪胀，随着含水率的降低，碎石土临胀状态明显提前，当含水率为7%时，转变为完全的剪胀。2) 从总体趋势来看，含水率越大，剪缩变形越大，剪缩持续时间越长，这是由于土体具有遇水软化特性，含水率越高，堆积碎石土软化现象越明显，土体内部的原有裂隙出现闭合，同时碎石土体发生塑性变形的能力增强，从而表现出了剪缩特性。

100 kPa围压下不同含石量时的剪胀特性如图6(c)所示。由图6(c)可知：在低围压下，碎石土在不同的含石量时发生剪胀。但与含水率的影响不同，并非线性变化，从图中曲线特征可以推断，碎石土存在一个最佳含石量使得碎石土压实最为紧密，强度最大。对比图6(b)与6(c)可见：在曲线前段发生剪缩时，不同含水率时的剪缩量与剪缩速率以及曲线的变化范围明显大于不同含石量时的剪缩量与剪缩速率以及曲线的变化范围，堆积碎石土的剪胀特性对含水率的变化更为敏感。

(a) 不同围压(P=60%，w=11%)；(b) 不同含水率(围压100 kPa)；(c) 不同含石量(围压100 kPa)

观察3个不同的变量，可以发现不论剪胀还是剪缩，曲线在生长到一定程度后就趋于平稳，此时，轴向应变在生长，而体积应变与轴向应力基本不变(试样开始破坏)，据此可作为碎石土剪切破坏的一个判断 依据。

在三维空间中剪胀定义为塑性体应变与塑性偏应变增量之比，即

刘萌成等[1]在此基础上定义了剪胀率为体应变与轴应变的增量比，即

根据式(4)，可以计算出不同质量密度及围压下的剪胀率。现以100 kPa围压，不同含水率为代表计算剪胀率。

不同含水率下的剪胀率与轴向应变关系如图7所示。图7中曲线特征表明：含水率为7%时，剪胀率均小于0，轴向应变很小时(1.25%)，剪胀率有一段减小的趋势。其他3种情况下剪胀率均由正转为负，且在正值阶段剪胀率也是先增大后减小。根据刘萌成 等[1]提出的剪胀率小于0时为剪胀，试样在含水率为7%时只发生剪胀，在其他3种含水率时先剪缩后剪胀。理论计算结果与实验结果一致。剪胀率为0代表试样处于临胀状态，含水率为9%，11%和13%时，对应的临胀状态的轴向应变分别为4.50%，10.01%和16.02%，含水率每增加2%，临胀状态就往后推迟5%左右。剪胀率在较小的轴向应变(4.50%左右)时变化最为剧烈，这说明不论是剪胀还是剪缩，试样在受剪初期变形是最快的。曲线发展到后期接近直线，剪胀率趋于稳定，表明试样进入临界状态。

w/%：1—7；2—9；3—11；4—13

Rowe[18]于1962年推出了塑性体应变增量比和有效应力比之间的关系，可以表达为

2.4 临界状态

Wood[19]定义土的临界状态为土在剪切过程剪应变能继续发展，而在应力和体积上没有进一步变化，可用下式表示][20]：

式中：′为有效中主应力；为偏应力；为塑性应变；为体积。

式中：为中主应力；为体应变。

图8 不同质量密度的体应变与中主应力的关系

式(7)和式(8)的方差分别为0.654和0.985，拟合效果较好。

这2条抛物型曲线之间，体应变有明显的两极分化，即明显的剪胀与剪缩，低中主应力(＜250 kPa)时为剪缩，高中主应力(＞300 kPa)时为剪胀，与2.3节中低围压发生剪胀，高围压发生剪缩一致。曲线有明显的峰值，代表在此峰值时不同质量密度和围压的组合为最优组合，使得堆积碎石土具有最大的体应变和抗剪能力。因此，在实际工程特别是重塑碎石土工程中，可以根据临界曲线求导得出极限值，通过预先埋设测试元件测出边坡中雨后土体的体应变变化趋势，从而判断出边坡的稳定性。此外，在重塑碎石土工程中，也可以对碎石土材料进行质量密度的配置，使重塑碎石土获得最高的抗剪强度。

3 结论

1) 碎石土在剪切过程中发生明显的鼓胀，围压越低鼓胀越大。剪切破坏时以破裂面的形式出现，成45°角。不同质量密度应力应变曲线有明显的台阶状，且围压较低时，台阶越明显；曲线在第1次峰值后出现应变硬化，第2次峰值后则出现应变软化(结构发生破坏)。含水率低于某值时(7%)，碎石土应力应变曲线为应变软化型，整体强度也并不会得到提高。碎石土的压硬性对于含石量的变化更为敏感。质量密度与围压之间存在联合影响。

2) 随着围压的增大，初始切线模量和剪切峰值都增大。含石量越大，初始切线模量和剪切峰值增长幅度越大。对于不同含水率，存在一个最佳含水率，使得堆积碎石土能充分发挥其力学性能。

3) 不同质量密度的堆积碎石土在剪切过程中有明显的剪胀特性。高围压时为剪缩，低围压时，先剪缩，后剪胀。从总体趋势来看，含水率越大，剪缩变形越大，剪缩持续时间越长，堆积碎石土的剪胀特性对含水率的变化更为敏感。对于不同的含石量，碎石土存在一个最佳含石量使得碎石土压实最为紧密，强速最大。

4)碎石土体应变在剪切后期趋于平缓，表明试验进入临界状态，不同质量密度及围压下的体应变主要集中在v=−17.29+0.078−6.72×10−52，v=−8.16+0.059− 5.83×10−52这2条曲线之间，将实际体变测试结果与曲线比较，作为连续强降雨雨后滑坡失稳临界状态的一个判断依据，甚至可根据曲线对重塑碎石土进行质量密度的配置。

[1] 刘萌成, 高玉峰, 刘汉龙. 堆石料剪胀特性大型三轴试验研究[J]. 岩土工程学报, 2008, 30(2): 205−210. LIU Mengcheng, GAO Yufeng, LIU Hanlong. Study on shear dilatancy behaviors of rockfills in large-scale triaxial tests[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(2): 205−210.

[2] 张兵, 高玉峰, 毛金生, 等. 堆石料强度和变形性质的大型三轴试验及模型对比研究[J]. 防灾减灾工程，2008, 28(1): 122−126. ZHANG Bing, GAO Yufeng, MAO Jinsheng, et al. Comparative research on the strength and deformation characteristics of rockfill materials in large-scale triaxial experiments and models analysis[J]. Disaster Prevention and Mitigation Engineering, 2008, 28(1): 122−126.

[3] 丁树云, 蔡正银, 毕庆涛. 堆石料的强度与变形特性及临界状态研究[J]. 岩土工程学报, 2010, 32(2): 248−252. DING Shuyun, CAI Zhengyin, BI Qingtao. Strength and deformation characteristics and critical state of rock fill[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(2): 248−252.

[4] 李兴瑞. 土石混合体的变形特性试验研究[D]. 辽宁: 大连理工大学土木工程学院, 2012: 32−33. LI Xingrui. The experimental study for deformation characteristics of earth-rock aggregate[D]. Liaoning: Dalian University of Technology. School of Civil Engineering, 2012: 32−33.

[5] 张家铭, 刘浩, 胡恒. 咸池沟弃渣场渣体大型三轴试验研究[J]. 工程勘察, 2012,12: 4−7. ZHANG Jiaming, LIU Hao, HU Heng. The Large-scale triaxial test research of waste residue of at Xian Chigou[J]. Engineering Investigation, 2012, 12: 4−7.

[6] 秦尚林, 陈尚维, 韩卓. 巨力土大型三轴试验研究[J]. 岩土力学, 2010, 33(2): 189−193. QIN Shanglin, CHEN Shangwei, HAN Zhuo. The large-scale triaxial experiments of Juli soil[J]. Rock and soil mechanics, 2010, 33(2): 189−193.

[7] 孔德志, 张丙印, 孙逊. 人工模拟堆石料颗粒破碎应变的三轴试验研究[J]. 岩土工程学报, 2009, 31(3): 464−469. KONG Dezhi, ZHANG Bingyin, SUN Xun. Triaxial tests on particle breakage strain of artificial rockfill materials[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(3): 464−469.

[8] Shafiee A. Permeability of compacted granule-clay mixtures[J]. Engineering Geology, 2008, 97(3/4): 199–208.

[9] 段祥宝, 刘运化, 杨超. 土体渗透变形及渗透破坏过程中分形特征初探[J].水电能源科学, 2013, 31(7): 100−103. DUAN Xiangbao, LIU Yunhua, YANG Chao. The process of the seepage deformation and seepage damage of soil fractal characteristics[J]. Water and Electricity Energy Science, 2013, 31(7): 100−103.

[10] WANG Yimin, CHEN Yekai, LIU Wei. Large-scale direct shear testing of geocell reinforced soil[J]. Journal of Central South University, 2008, 15(6): 895−900.

[11] 梁燕, 李同录, 李家春. 临河碎石土路堤稳定性的试验研究[J]. 广西大学学报, 2010, 35(5): 711−718.LIANG Yan, LI Tonglu, LI Jiachun. Study on the stability of the detritus embankment a long river[J]. Journal of Guangxi University, 2010, 35(5): 711−718.

[12] 魏松, 朱俊高. 粗粒料三轴湿化颗粒破碎试验研究[J]. 岩石力学与工程学报, 2006, 25(6): 1252−1258. WEI Song, ZHU Jungao. Sudy on wetting breakage ofcoarse-grained materials in triaxial test[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(6): 1252−1258.

[13] 朱俊高, 刘忠, 翁厚洋. 试样尺寸对粗颗粒土强度及变形试验影响研究[J]. 四川大学学报, 2012, 44(6): 92−96. ZHUN Jungao, LIU Zhong, WENG Houxiang. The test study of Sample size to strength and deformation of coarse particle[J]. Journal of Sichuan University, 2012, 44(6): 92−96.

[14] 丁秀丽, 李耀旭, 王新. 基于数字图像的土石混合体力学性质的颗粒流模拟[J]. 岩石力学与工程学报, 2010, 29(3): 477−484.DING Xiuli, LI Yaoxu, WANG Xin. Particle flow modeling mechanical properties of soil and rock mixtures based on digital image[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(3): 477−484.

[15] 钱家欢, 殷宗泽. 土工原理与计算[M]. 北京: 中国水利水电出版社, 1996: 54−56. QIAN Jiahuan, YIN Zongze. Geotechnical principle and calculation[M]. Beijing: China Water Power Press, 1996: 54−56.

[16] 王靖涛. 论岩土塑性体应变与剪应变的相互作用原理[J]. 中国工程科学, 2006, 8(9): 24−29. WANG Jingtao. Demonstration of the principlep of interaction between plastic volume strain and shear for rock and soil[J]. China Engineering Science, 2006, 8(9): 24−29.

[17] 鹿英奎. 土的剪胀机理及试验研究[D]. 北京: 北方工业大学建筑工程学院, 2012: 26−27. LU Yingkui. Study on dilatancy mechanism and test of soil[D]. Beijing: North China University of Technology. Construction Engineering College, 2012: 26−27.

[18] Rowe P W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact[J]. Proc Roy Soc A, 1962, 269: 500−527.

[19] Wood D M. Soil behaviour and critical state soil mechanics[M]. Cambridge: Cambridge University Press, 1990: 150−160.

[20] 杨迎晓, 龚晓南, 范川, 等. 钱塘江冲海积非饱和粉土剪胀性三轴试验研究[J]. 岩土力学, 2011, 32(1): 39−42. YANG Xiaoying, GONG Xiaonan, FAN Chuan, et al. Triaxial testing study of dilatant characteristics of Qiantangjiang alluvial unsaturated silts[J]. Rock and soil mechanics, 2011, 32(1): 39−42.

Analysis of deformation characteristics of eluvialgravel soil under mass density and confining pressure

DONG Hui1, 2, HU Ziran1, FU Helin3, CHEN Cheng1, CHEN Xiwen1

(1. College of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105, China;2. Institute of Rheological Mechanics, Xiangtan University, Xiangtan 411105, China;3. School of Civil Engineering, Central South University, Changsha 410075, China)

Considering the influence of mass density (the different stone content, moisture content) and confining pressure on gravel soil deformation characteristics, an experiment of gradation representative sample eluvial gravel soil of Zhaoshan Hunan province was carried out. The results show that the mass density and confining pressure have a combined effect. Gravel soil stress-strain curve under the different mass density shows as step-like, that is strain at first hardening then softening, strain softening for moisture content of 7%. With the increase of the confining pressure, the initial tangent modulus and shear peak value increase, but non-linear growth with the change of the mass density, the yield locus into parallel lines. Shear contraction under low confining pressure, the high confining pressure dilatation. The pressure-sensitivity of eluvial gravel soil is more sensitive to stone content, the shear dilatation is more sensitive to moisture content, and there are optimum moisture content and the best stone content. Dilatancy rate and effective stress ratio can be a judgment of the dilatancy property. Also volumetric strain is found on different mass density and confining pressure are mainly concentrated in two curves. It can be a judgment for landslide failure after continuous heavy rainfall.

landslide; gravel soil; mass density; pressure-sensitivity; shear dilatation

10.11817/j.issn.1672-7207.2015.10.043

TU411

A

1672−7207(2015)10−3879−09

2015−02−06；

2015−05−20

国家自然科学基金资助项目(51108397)(Project (51108397) supported by the National Natural Science Foundation of China)

董辉，博士研究生，副教授，从事智能岩土信息技术、滑坡防灾减灾研究；E-mail：aneurin.h.d@gmail.com

(编辑 陈爱华)