早期帕金森疾病脑电信号的复杂度分析
2015-10-09刘哲,王江
刘 哲,王 江
(天津大学电气与自动化工程学院,天津 300072)
帕金森疾病是一种常见的神经退行性疾病。其临床症状主要表现为运动障碍,例如静息性震颤、运动迟缓、僵硬和姿势不稳等[1]。此外,大部分患者还会出现自主神经功能障碍、认知功能损伤、睡眠障碍和精神困扰等[1]。据统计,全世界超过55岁的人口中大约有1%的人患有帕金森症,同时患者数目每年都会增加[2-3]。目前,对于该病的临床诊断主要是基于病人的病史和身体检查,但是临床诊断的准确性只有80%~90%。这主要是由于帕金森病的临床特点并非仅仅适用于帕金森,尤其是其早期症状经常与正常年龄老化过程中出现的身体状况或运动能力退化相混淆。因此,急需新的手段来对帕金森疾病进行诊断,尤其是早期诊断,这对该病的有效治疗至关重要。
脑电图(electroencephalogram,EEG)是一种记录大脑电波变化的非侵入式技术,具有高时间分辨率和低空间分辨率的特点[4-5],它不仅包含了大量脑功能信息,而且能反映很多疾病的皮层功能异常。因此,临床上常被用来探索脑功能工作机制以及描述与神经病理学相关的脑电节律特征。研究发现,采用非线性方法量化脑电信号能够为诊断很多神经精神疾病提供可靠的生物指标,比如帕金森症、精神分裂症、重度抑郁症和老年痴呆症等[6-9]。目前,它已成为神经病学里最广泛的临床诊断工具,对疾病的早期检测和早期介入非常关键。
通过分析EEG功率谱发现,帕金森病人最普遍的脑电异常是大脑活动减缓[10]。主要体现在与健康对照组相比,非痴呆的帕金森病人在静息状态下的脑电β频带功率谱降低[11-12],θ和α频带功率谱明显升高[10,13]。 最近,STOFFERS等[10]进 一步证明了脑活动普遍减缓是非痴呆性帕金森症的一个稳定特征,并且第1次提出这种异常的脑活动在未经治疗的早期帕金森患者中已经存在。此外,STOFFERS等[14]还刻画了帕金森病人在静息状态下的θ,α和β节律的同步变化。研究发现,α频带功能连接增加是帕金森症的早期临床特点。随着病程的不断迁延,θ和β频段的功能连接也会随之增加。
近期,很多学者采用不同的非线性算法量化EEG时间序列的复杂度特征。研究发现,脑电信号复杂度的高低蕴含了皮层活动在不同状态下的重要信息。这对探索由帕金森症导致的认知功能异常有很大的帮助。在较早的研究中,STAM等[11,15]采用关联维数和最大李雅谱诺夫指数刻画了帕金森患者EEG信号的复杂度。结果发现,相比于对照组,在静态下其脑电复杂度明显减低[11,15],在非静息状态下其脑电复杂度升高[16]。但是,这两种复杂度算法需要信号是长时间平稳且无噪声,这对于EEG数据是不容易满足的。此外,GÓMEZ等[17]采用 Lempel-Ziv复杂度刻画帕金森症的MEG活动特征,发现早期帕金森病人所有通道的MEG信号的复杂度与对照组相比均有所降低。但是,Lempel-Ziv复杂度算法是一种对数据粗粒化处理的方法,在这个过程中原数据的一些重要信息可能会丢失。
基于上述研究现状,本文提出采用两种基于排序的非线性算法定量研究帕金森病人脑电信号的复杂度,二者分别是排列熵(PE)[17]和规则性指数(OI)[18]。原因是,这两种基于数据排序模式的算法特别适合分析不平稳的时间序列,例如EEG信号。相比于传统复杂性算法,它们有许多明显的优势,比如定义简单、运算快、鲁棒性强以及具有非线性单调转换不变性[17]等。目前,二者已被成功地应用于刻画癫痫和麻醉状态下EEG信号的复杂度[19-22]。
1 实验部分
1.1 实验对象
本文中的实验组和对照组的EEG数据均来自于天津市环湖医院,实验时间为2010年5月至2010年8月。其中实验患者组成员为27名临床诊断为早期帕金森疾病患者(12男,15女,平均年龄为61.1±7.7岁),对照组成员为27名年龄和性别与实验组相当的健康受试者(12男,15女,平均年龄为60.8±8.6岁)。在测取EEG数据前,他们均被告知了实验的目的和进程,并获得了他们的知情同意书。所有受试者均未服用神经安定药、抗抑郁药和多巴胺阻断剂等药物,同时他们也不曾患有其他神经精神疾病。
对帕金森患者的疾病诊断依据是病史、神经系统和身体检查、以及对左旋多巴的药物反应。他们患帕金森的平均时间为(3.9±1.6)年(浮动范围:1~6.2年)。Hoehn和Yahr等级为1~2,其中10人在第1级、9人在1.5级、8人在第2级。简易精神状态检查(MMSE)平均得分为28.1±1.2(变动范围:27~30),均属于正常范围。此外,为了降低药物异质性,所有帕金森患者都曾服用左旋多巴药物,但是实验前半个月内均停止服药。
对照组的所有受试者都是健康的,没有神经精神疾病史。所有人的神经系统检查都是正常的,简易精神状态检查得分为29.0±0.8(浮动范围:28~30)。
1.2 EEG数据记录
整个测量过程在一个安静、昏暗的屏蔽室内进行。测量过程中,所有受试者均闭眼,并且直立地坐在躺椅上以达到轻松清醒的状态。通过一台Neuroscan系统记录头皮脑电图。20个Ag-AgCl记录电极依据国际10—20导联标准放置在头皮上,如图1所示,耳朵作为参考电极。EEG信号的采样频率为256Hz,带通滤波器范围为0.25~75Hz。对每一个受试者,挑选一段80s长的纯净脑电数据用于分析。这段数据中不含肌电、眼动或者其他干扰,如图2所示。

图1 国际标准10—20系统电极安放位置Fig.1 International 10-20system for EEG electrode placement
2 复杂度算法
2.1 排序熵
排序熵(PE)最先是由BANDT和POMPE提出的,它是将连续时间信号映射到一个符号序列中[19]。给定一个标量时间序列(x1,x2,…,xn),首先把它嵌入到一个m维相量空间中。通过这个嵌入过程,可以得到矢量Xi=[x(i),x(i+t),…,x(i+(m-1)t)],其中m是嵌入维度,t是延迟时间。然后将矢量Xi按照降序或者升序排列。对于m个不同数,会有m!种可能的排列方式,也被称为排序模式,记为π。这样,任一矢量Xi都能被唯一地映射到(q1,q2,…,qm),这是m!种排序模式中的一种。令pj(j=1,2,…,m!)表示排序pj出现的概率。那么,序列(x1,x2,…,xn)的PE可被定义为[20-21]:

图2 两组对象的C4导和F3导脑电信号Fig.2 EEG signals in C4and F3channel for two groups

正规化后有[20-21]
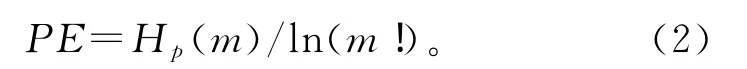
显然,当所有排序模式出现的概率相同时,PE值为1。此时,意味着时间序列是完全随机的。和其他熵一样,PE是衡量时间序列的不确定性和可预测性的一种方法[19]。时间序列越规律,PE值越小。
2.2 规则性指数
规则性指数(OI)作为一种复杂度测量方法,最初是由OUYANG等[18]提出用来分析癫痫脑电数据的。对于给定脑电图序列(y1,y2,…,yn),通过对其数据进行随机重排,可生成一个替代时间序列(s1,s2,…,sn)。新生成的替代序列s(i)和最初的脑电图序列y(i)有相同的分布,但其排序模式被打乱。然后,将原始序列y(i)和新序列s(i)嵌入到一个m维相空间中。这样,就形成2个不同的向量Yi=[y(i),y(i+t),…,y(i+(m-1)t)]和Si=[s(i),s(i+t),…,s(i+(m-1)t)]。对 于 向 量Yi,计算其各个排序模式的概率分布,并用py(pi)(i=1,2,…,m!)来表示。按照递减的顺序对py(pi)进行排序,从而获得一个新的概率分布py(pRi)(i=1,2,…,m!)。在这个概率分布序列中,py(pR1)为序列中出现频率最高的排序模式的概率,py(pRm!)为出现频率最低的排序模式的概率。时间序列的规则性指数(OI)[19]见式(3)。
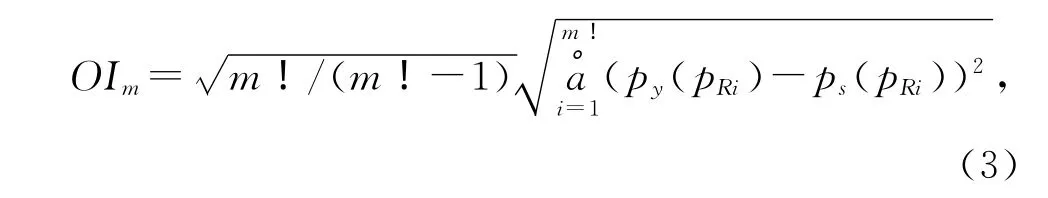
式中,py(pRi)和ps(pRi)分别表示原始脑电图序列y(i)和替代序列s(i)的概率分布。为了简化计算,OUYANG等[19]提出假定任何排序模式以相同的概率出现在替代序列中。这样,ps(pRi)成为了均匀分布。
PE和OI都是刻画时间序列复杂度的算法。和PE相反,高OI值表示脑电序列包含更多的规则和确定性的信息,低OI值表示脑电序列中有更多的随机或不确定的信息[19]。总而言之,一个高复杂度的脑电图序列对应的PE值较高、OI值较低,一个低复杂度的脑电图序列对应的PE值较低、OI值较高。
在计算过程中,首先采用滑动窗对EEG数据进行切分。滑动窗长4s,滑动步长为1s,这样每个窗口内包含1 024个数据点。然后利用PE和OI算法对每个数据块进行处理。PE和OI的计算均依赖于嵌入维度m和延迟时间t[20-21]。根据文献[20]可知,当脑电图数据长度为N=1 024时,嵌入维数取m=5效果最好。延迟时间是通过文献[23]提出的最佳嵌入算法确定的,经过计算得t=1。
3 结 果
首先,对每个通道EEG数据的复杂度进行量化。为了跟踪脑电复杂度的瞬态变化,分别计算每个时间窗内的复杂度指标。图3和图4刻画了以图2中2位受试者C4和F3导联脑电信号为例的分析结果,分别反映了单个导联EEG信号的PE和OI随时间的变化情况。从这两组图中可以看出,与健康的对照者相比,早期帕金森患者的脑电信号在大部分时间内有较低的PE值和较高的OI值。
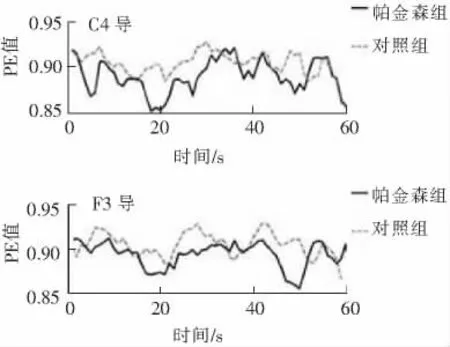
图3 C4导和F3导脑电信号排序熵Fig.3 Permutation entropy of the EEG signals in C4and F3channel

图4 C4导和F3导脑电信号规则性指数Fig.4 Order index of the EEG signals in C4and F3channel
其实,对每个通道内所有时间窗的PE值和OI值取平均,可得到每位受试者在该通道内的复杂度测量。图5中的脑地形图分别刻画了所有受试者的20导EEG信号的平均PE值和平均OI值的分布情况。从图中可以发现,与健康对照组相比,早期帕金森患者的20导EEG信号均呈现出较低的PE值和较高的OI值。图5也给出了2个实验组的平均PE和平均OI的单因素方差统计结果,显著性水平P<0.05的EEG通道已用黑色实心圆点标出。可以发现,在额叶、顶叶、枕叶和颞叶区域的相应导联上,两组受试者之间的复杂度有统计学上的显著性差异。
最后,计算了2组受试者全脑20导EEG数据的平均PE值和平均OI值,同时利用单向方差分析统计了这2个复杂度指标所对应的P值。图6和图7的箱线图分别显示了全脑20导EEG数据的平均PE值和OI值。由图6和图7可知,早期帕金森患者的PE值低于对照组,OI值高于对照组,二者均具有统计意义上的差别(P<0.05)。这表明,早期帕金森患者脑电序列的复杂度低于健康对照组。
4 结 语
为了刻画早期帕金森疾病脑活动的复杂度异常,采用了PE和OI这2种基于时间序列排序模式的度量方法,分析了27名早期帕金森患者和27名健康对象在静息状态下的EEG活动,其中帕金森患者的平均患病时间为(3.9±1.6)年(浮动范围:1~6.2年),Hoehn和Yahr等级均低于2级。研究发现,与对照组相比,早期帕金森患者EEG序列的PE值降低、OI值升高,说明其脑活动的复杂度降低。这些复杂度的异常变化可能与患者早期轻微的认知障碍密切相关。研究结果表明,基于排序模式的复杂度算法可以为检测早期帕金森症提供一个定量的生理指标。这对于帕金森疾病的早期诊断和有效治疗具有重大意义。
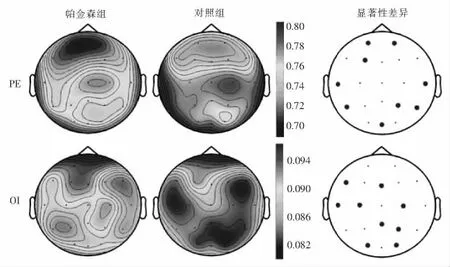
图5 2组实验者平均PE和平均OI的脑地形图及单因素方差统计结果Fig.5 Brain topography of the average PE and OI values for two groups as well as their one-way ANOVA analysis results

图6 脑电信号排序熵的箱线图Fig.6 Boxplots of the permutation entropy of the EEG signals

图7 脑电信号规则性指数的箱线图Fig.7 Boxplots of the order index of the EEG signals
/References:
[1]乐亮,黎仕锋,王友琼,等.帕金森病的研究现状[J].中山大学研究生学刊(自然科学、医学版),2009,30(4):1-6.LE Liang,LI Shifeng,WANG Youqiong,et al.A review on Parkinson’s disease[J].Journal of the Graduates Sun YAT-SEN University(Natural Sciences,Medicine),2009,30(4):1-6.
[2]DAS R.A comparison of multiple classi cation methods for diagnosis of Parkinson disease[J].Expert Systems with Applications,2010,37:1568-1572.
[3]陈茹.帕金森病研究进展[J].中国康复理论与实践,2007,13(7):637-639.CHEN Ru.Advance in Parkinson’s disease(review)[J].Chinese Journal of Rehabilitation Theory and Practice,2007,13(7):637-639.
[4]边洪瑞,王江,韩春晓,等.基于复杂度的针刺脑电信号特征提取[J].物理学报,2011,60(11):118701.BIAN Hongrui,WANG Jiang,HAN Chunxiao,et al.Features extraction from EEG signals induced by acupuncture based on the complexity analysis[J].Acta Physica Sinica,2011,60(11):8701-8709.
[5]孙红敏,边志杰,崔冬,等.普拉提运动想象的脑电功率谱分析[J].燕山大学学报,2012,36(5):458-464.SUN Hongmin,BIAN Zhijie,CUI Dong,et al.Power spectral analysis of EEG during pilates motor imagery[J].Journal of Yanshan University,2012,36(5):458-464.
[6]GANDAL M J,EDGAR J C,KLOOK K,et al.Gamma synchrony:Towards a translational biomarker for the treatmentresistant symptoms of schizophrenia[J].Neuropharmacology,2012,62(3):1504-1518.
[7]KLASSEN B T,HENTZ J G,SHILL H A,et al.Quantitative EEG as a predictive biomarker for Parkinson disease dementia[J].Neurology,2011,77(2):118-124.
[8]HAMPEL W H,FRANK R,BROICH K,et al.Biomarkers for Alzheimer’s disease:Academic,industry and regulatory perspectives[J].Nature Reviews Drug Discovery,2010,9(7):560-574.
[9]LEUCHTER A F,COOK I A,CILMER W S,et al.Effectiveness of a quantitative electroencephalographic biomarker for predicting differential response or remission with escitalo-pram and bupropion in major depressive disorder[J].Psychiatry Research,2009,169(2):132-138.
[10]STOFFERS D,BOSBOOM J L,DEIJEN J B,et al.Slowing of oscillatory brain activity is a stable characteristic of Parkinson’s disease without dementia[J].Brain,2008,130(7):1847-1860.
[11]STAM K J,TAVY D L,JELLES B,et al.Non-linear dynamical analysis of multichannel EEG:Clinical applications in dementia and Parkinson’s disease[J].Brain Topography,1994,7:141-150.
[12]PEZARD L,JECH R,RUZICKA E.Investigation of non-linear properties of multichannel EEG in the early stages of Parkinson’s disease[J].Clinical Neurophysiology,2001,112:38-45.
[13]TANAKA H,KOENIG T,PASCUAL-MARQUI R D,et al.Event-related potential and EEG measures in Parkinson’s disease without and with dementia[J].Dementia and Geriatric Cognitive Disorders,2000,11(1):39-45.
[14]STOFFERS D,BOSBOOM J L,DEIJEN J B,et al.Increased cortico-cortical functional connectivity in early-stage Parkinson’s disease:An MEG study[J].NeuroImage,2008,41(2):212-222.
[15]STAM C J,JELLES B,ACHEREEKTE H A,et al.Investigation of EEG non-linearity in dementia and Parkinson’s disease[J].Electroencephalography and Clinical Neurophysiology,1995,95(5):309-317.
[16]MULLER V,LUTZENBERGER W,PULVERMULLER F,et al.Investigation of brain dynamics in Parkinson’s disease by methods derived from nonlinear dynamics[J].Experimental Brain Research,2001,137(1):103-110.
[17]GÓMEZ C,OLDEDUBBELINK K T,STAM C J,et al.Complexity analysis of resting-state MEG activity in early-stage Parkinson’s disease patients[J].Annals of Biomedical Engineering,2011,39(12):2935-2944.
[18]BANDT C,POMPE B.Permutation entropy:Anatural complexity measure for time series[J].Physical Review Letters,2002,88(17):4102-4107.
[19]OUYANG G,DANG C,RICHARDS D A,et al.Ordinal pattern based similarity analysis for EEG recordings[J].Clinical Neurophysiology,2010,121(5):694-703.
[20]CAO Y,TUNG W W,GAO J B,et al.Detecting dynamical changes in time series using the permutation entropy[J].Physical Review E,2004,70:046217.
[21]LI D,LI X,LIANG Z,et al.Multiscale permutation entropy analysis of EEG recordings during sevoflurane anesthesia[J].Journal of Neural Engineering,2010,7(4):6010-6016.
[22]LI X,OUYANG G,RICHARDS D A.Predictability analysis of absence seizures with permutation entropy[J].Epilepsy Research,2007,77(1):70-74.
[23]GAO Jianbo,ZHENG Zhemin.Local exponential divergence plot and optimal embedding of a chaotic time series[J].Physics Letters A,1993,181(2):153-158.
