调和映照与像域为线性连结的剪切函数的关系
2015-09-29占龙俊黄心中
占龙俊,黄心中
(华侨大学数学科学学院,福建泉州362021)
调和映照与像域为线性连结的剪切函数的关系
占龙俊,黄心中
(华侨大学数学科学学院,福建泉州362021)

调和映照;线性连结;调和拟共形映照;α近于凸.
1 预备知识
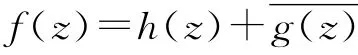
Huang[3]对Chuaqui等[2]所得的结论进一步推广,得到不少有趣的成果.Huang[3]还特别指出,在一定条件下,f(D)的线性连结性与f(z)的拟共形性,及h(D)线性连结性与h(z)的单叶性是一对不变量.文献[6-8]分别对单叶调和映照的性质及稳定性问题进行研究.

Chen等[10]证明了定理C[2].
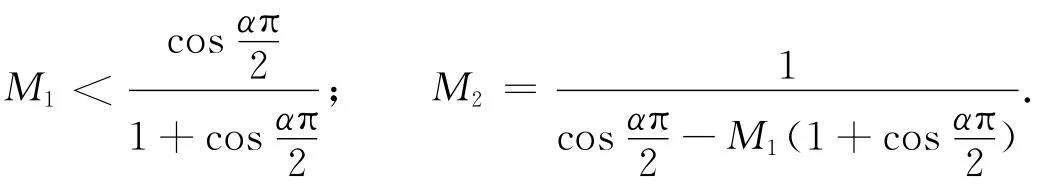

2 主要结果及证明
证明 假设F(z)=h(z)-g(z),若h(z)在D上不单叶,则存在z1,z2∈D,且z1≠z2,使得h(z1)=h(z2).由h(z)=F(z)+g(z),则F(z2)-F(z1)=g(z1)-g(z2).根据F(z)的单叶性,令w=F(z)有w2-w1=g(F-1(w1))-g(F-1(w2)).由于F(D)是M-线性连结区域.则存在连结w1-w2∈F(D)的可求长曲线γ∈F(D)满足l(γ)≤M|w1-w2|,即

这与w2-w1=g(F-1(w1))-g(F-1(w2))矛盾,从而说明h(z)在D上单叶.
令ξ=h(F-1(w))=w+g(F-1(w)),任意ξ1,ξ2∈h(D),存在w1,w2∈F(D),使ξ1=h(F-1(w1)),ξ2=h(F-1(w2)).由于F(D)是M-线性的连结区域,则存在γ为连结w1,w2的曲线,使l(γ)≤M|w1-w2|.取Γ=h(F-1(γ)),有
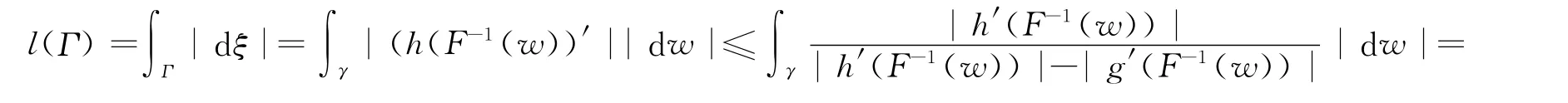
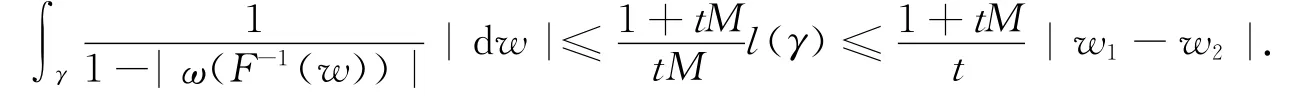
又

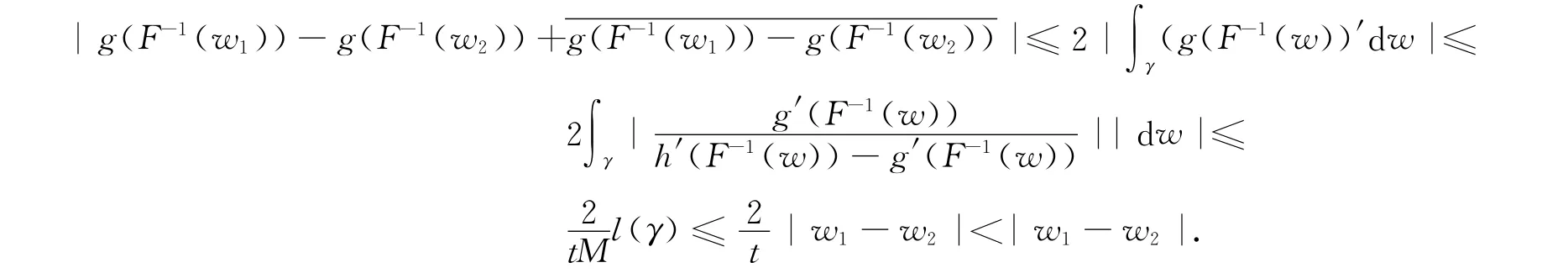

又

相应于定理C的结果,进一步研究其参数化的情况,得到定理2.
证明 因F(z)为D上α近于凸映照,由文献[6]得F(z)在D上的单叶,且F(D)是1/cos(απ/2)-线性连结区域,则由定理C可得h(z)在D上的单叶.
令ξ=h(F-1(w))=w+g(F-1(w)),任意ξ1,ξ2∈h(D),存在w1,w2∈F(D),使ξ1=h(F-1(w1)),ξ2=h(F-1(w2)).由于F(D)是1/cos(απ/2)-线性连结区域,则存在γ为连结w1,w2的曲线,使l(γ)≤1/cos(απ/2|w1-w2|).取Γ=h(F-1(γ)),有
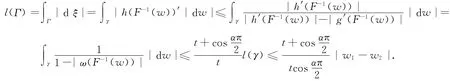
又

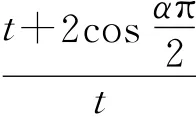
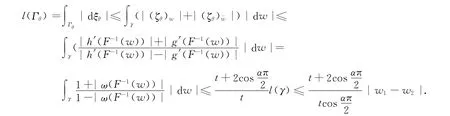
又

注1 注意到当|λ|<1时,这时t可以取到小于2的常数.



又

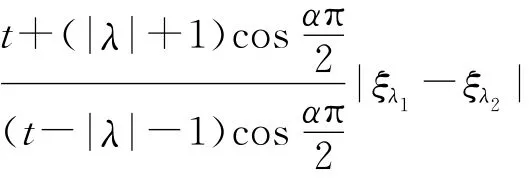
对于fλ(z)=h(z)+λg(z)时,采用相同的证明方法,可得到定理3中的结论.定理3证毕.
在定理1,2,3中,若F(z)=h(z)+g(z)有相应的假定,结论仍是成立的.
[1] LEWY H.On the non-vanishing of the jacobian in certain one-to-one mappings[J].Bull Amer Math Soc,1936,42(10):689-698.
[2] CHUAQUI M,HERNANDEZ R.Univalent harmonic mappings and linearly connected domains[J].J Math Anal Appl,2007,33(2):1189-1194.
[3] HUANG Xin-zhong.Locally univalent harmonic mappings with linearly connected image domains[J].Chinese Ann Math Ser A(Chinese),2010,31A(5):625-630.
[4] 王其文,黄心中.某些调和函数的系数估计与像区域的近于凸性质[J].华侨大学学报:自然科学版,2013,34(2):225-229.
[5] 石擎天,黄心中.调和映照与其剪切函数的单叶性[J].华侨大学学报:自然科学版,2013,34(3):334-338.
[7] HUANG Xin-zhong.Harmonic quasiconformal mappings on the upper half-plane[J].Complex Variables and Elliptic Equations,2013,58(7):1005-1011.
[8] 夏小青,黄心中.一类双调和映照的单叶半径估计[J].华侨大学学报:自然科学版,2011,32(2):218-221.
[9] POMMERENKE C.Boundary behaviour of conformal maps[M].Berlin:Springer-Verlag,1992:106-107.
[10] CHEN Shao-lin,PONNUASMY S,RASILA A,et al.Linear connectivity,Schwarz-Pick lemma and univalency criteria for planar harmonic mappings[EB/OL].[2015-01-05].http://arxiv.org/abs/1404.4155.
Relation Between Harmonic Mapping and Its Shear Function With Linearly Connected Image Domain
ZHAN Long-jun,HUANG Xin-zhong
(School of Mathematical Sciences,Huaqiao University,Quanzhou 362021,China)
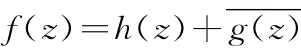
harmonic mapping;linearly connected domain;harmonic quasiconformal mapping;α-close-to convex
陈志贤 英文审校:黄心中)
O174.51;O174.55文献标志码: A
1000-5013(2015)05-0603-06 doi:10.11830/ISSN.1000-5013.2015.05.0603
2015-01-05
黄心中(1957-),男,教授,博士,主要从事函数论的研究.E-mail:huangxz@hqu.edu.cn.
国家自然科学基金资助项目(11471128);福建省自然科学基金资助项目(2014J01013)
