浅谈小学数学解答应用题的思考方法

刁攀利

【摘 要】 应用题是小学数学教学中一个非常重要的内容。解答应用题，能够开始孩子的智力，培养与提高分析问题和解决问题能力。

【关键词】应用题；综合法；分析法

解答应用题又是数学教学中一个难点，因为应用题中有些数量关系比较抽象、隐蔽，有些学生没有掌握分析数量关系的方法，所以解题时常常感到束手无策。在解答应用题的全部过程中，分析应用题的数量关系是解题的关键。因此，必须学会分析应用题的思考方法。

分析应用题的思考方法有两种，一种是综合法，另一种是分析法。综合法是从应用题的已知条件出发，逐步推算出要解决的问题，分析法是从应用题所要解决的问题出发，逐步找出要解决的问题所必需的已知条件。下面用一个例题分别说明这两种方法。

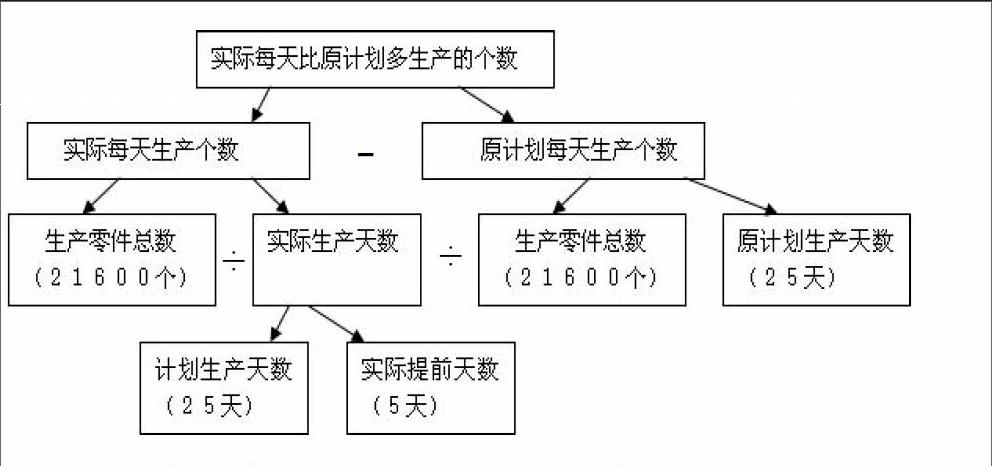
如：一个车间计划在25天内生产机器零件21600个。由于改进技术，实际比原计划提前5天完成，这个车间每天比原计划多生产多少个零件？

1.用综合法分析

由于计划25天，生产机器零件21600个这两个条件，可以求出原计划每天生产的零件个数；

由于计划25天，实际提前5天完成任务这两个条件，可以求出实际生产的天数；

由实际生产的天数和生产机器零件的总数这两个条件，可以求出实际每天生产的个数；

由实际每天生产的个数和原计划每天生产的个数这两个条件，即可求出每天比原计划多生产的零件个数。

这个分析过程可用下图表示：

-

÷ ÷

-

这个图叫做综合法思路图。从这个图可以看出：用综合法分析复合应用题，就是从应用题的已知条件出发，运用已学过的简单应用题知识，由已知条件逐步推出所要解决的问题。

2.用分析法分析

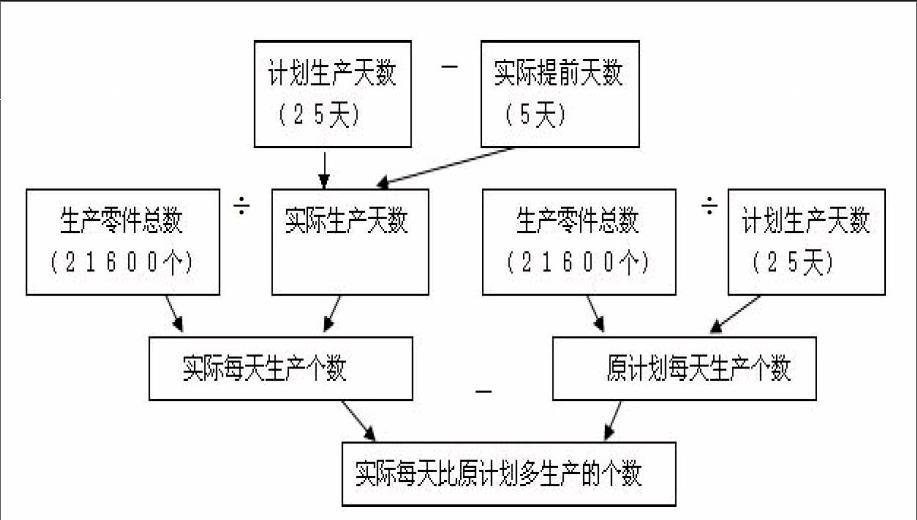
要求出实际每天比原计划多生产多少个，必须知道：实际每天生产的个数和原计划每天生产的个数。

要求出每天生产的个数， 必须知道： 生产零件总数（21600个）和实际生产的天数。

要求出实际生产的天数，必须知道：原计划生产的天数（25天）和实际提前的天数（5天）。题中，这两个数都是已知的。

要求出原计划每天生产的个数，必须知道：生产零件总数（21600个）和原计划生产的天数（25天）。题中，这两个数都是已知的。

经过分析，从题中找到了已知条件，问题就全部解决了。

这个分析过程可用下图表示：

■

这个图叫做分析法思路图。从这个图可以看出：用分析法分析复合应用题，就是从应用题的所求问题出发，运用已学过的简单应用题的知识，找出解决这个问题所需的两个条件，如果题中没有直接告诉这两个条件，就继续分析，一直到所需的条件都是已知数为止。

从以上分析中，我们可以看到，一道复合应用题，是由几个简单应用题组合成的。所以解答一般的复合应用题，关键在于分析数量关系，找到隐藏的中间量，提出中间问题，把一道复合应用题分解成几个有连续性的简单应用题，这样就可以找到解题的方法。

综合法与分析法的思考方向是完全相反的。但是这两种思考方法并不是对立的，而是相互联系的。在分析解答应用题的过程中，这两种方法经常是互相配合使用的。用综合法分析应用题时，要随时注意要解决的问题。用分析法分析时，要随时注意题中的已知条件。这样才能提高分析问题和解决问题的能力。

分析应用题的数量关系时，有时还可以采用画线图、列表等辅助方法，使抽象问题具体化，形象化，来帮助理解题意，分析题中的数量关系。

【参考文献】

[1]柳直东，宋盛玲，兰兰，张文培，尹晴晴，陈家翠.城郊结合部中学开设研究性学习的研究与实践[Z].国家科技成果

[2]中华人民共和国教育部.全日制义务教育《数学课程标准》（实验稿）.北京：北京师范大学出版社.2001

（作者单位：重庆市江津区双槐树小学）