未知环境下异构多无人机协同搜索打击中的联盟组建
2015-09-27刘重高晓光符小卫牟之英西北工业大学电子信息学院陕西西安709航空电子综合技术重点实验室上海0033
刘重,高晓光,符小卫,牟之英(.西北工业大学电子信息学院,陕西西安709;.航空电子综合技术重点实验室,上海0033)
未知环境下异构多无人机协同搜索打击中的联盟组建
刘重1,高晓光1,符小卫1,牟之英2
(1.西北工业大学电子信息学院,陕西西安710129;2.航空电子综合技术重点实验室,上海200233)
为了提高多架异构无人机在未知环境下协同执行搜索打击任务时的效能,提出了一种未知环境下的异构多无人机协同搜索打击中的联盟组建方法,研究了实时性较高且适应于未知环境下的任务分配机制。以最小化目标打击时间和最小化联盟规模为优化指标,以满足同时打击和资源需求为约束条件,建立了联盟组建模型;为了提高联盟组建的实时性,提出了一种分阶次优联盟快速组建算法(MSOCFA)。算法复杂度分析说明了该算法是一个多项式时间算法,并且通过与粒子群优化算法进行仿真对比,验证了该算法具有较低的计算复杂度,满足实时性要求。为了使得多架无人机能自主协同完成搜索打击任务,设计了基于有限状态机(FSM)的多无人机分布式自主协同控制策略。仿真验证了未知环境下的异构多无人机协同搜索打击中的联盟组建方法的合理性和可行性。使用蒙特卡洛法验证了无人机数量和目标数量对联盟组建的影响,即无人机数量越多,目标数量越少,其平均任务完成时间越短。
控制科学与技术;多无人机;协同搜索打击;联盟组建;有限状态机;蒙特卡洛方法
0 引言
无人机具有零伤亡、高机动性、隐身性能好、费用低等优势,被广泛应用于作战环境中的搜索打击任务。然而,面对日趋复杂的现代战场环境,由于单架无人机的性能受到载荷等限制,执行对多目标的作战任务必须要多架异构无人机协同才能完成。多架异构无人机能够有效执行对多目标搜索打击任务的前提是多无人机之间能够进行有效的任务分配[1]。
针对任务分配问题,许多学者进行了研究并取得了一系列成果,提出了诸如动态网络流优化(DNFO)、混合整数线性规划(MILP)、多维多选择背包问题(MMKP)及多无人机协同多任务分配问题(CMTAP)等模型来解决任务分配问题。文献[2-3]在研究广域搜索攻击问题时,以无人机为供应商,任务为网络上的物流,任务分配的结果作为需求,无人机执行任务的代价或收益作为任务在网络中流动的代价,建立DNFO模型,通过对网络流量总代价最小化实现多无人机任务分配。文献[4-6]针对多架同构无人机执行空对地攻击任务问题,建立了相应的MILP模型,在该模型中假设无人机在执行了攻击任务后会损伤而不能继续执行其他任务,因此要求无人机的数目多于目标的数目。在此基础上,文献[7]以多架无人机执行压制敌防空系统任务为背景,建立了相应的MILP模型。文献[8]将多无人机任务分配描述为多维多选择背包问题。文献[9]以最小化所有无人机的飞行距离或者完成任务的时间为优化目标,建立了多无人机协同多任务分配模型,利用遗传算法对该模型进行了求解。此外,还有应用合同网[10]、基于多智能体满意决策论[11]等方法求解多无人机任务分配。总的来说,上述方法存在着这样的问题:1)现有无人机任务分配模型和方法中通常假设无人机是同构的并且不考虑资源的消耗,与实际作战不符;2)任务分配问题的求解方法实时性不高;3)需要预先知道目标的数量、位置等信息。然而多架无人机协同执行搜索打击任务时,由于环境的未知不确定性,目标的数量、位置等信息对无人机来说事先是未知的。因而上述问题对传统的多无人机任务分配方法提出了挑战。
多无人机系统可看作是多Agent系统(MAS). 在MAS中,当单个Agent不能或不能有效完成特定的任务时,Agent就必须形成联盟来完成。联盟是为完成某个共同任务而结合在一起的多个个体。通过组建联盟实现任务分配,在多机器人(MRS)领域也得到了深入的研究,因此可以借鉴MAS和MRS中联盟组建的思路来解决多架异构无人机协同执行搜索打击任务时的任务分配问题。文献[12]以对策论中的多人合作博弈为基础,采用分布式问题求解(DPS)方法从无联系的多Agent构建出有联系的多Agent联盟,以解决多Agent任务分配问题。在文献[12]的基础上,文献[13-14]针对竞争环境下MRS联盟组建问题,提出一种基于市场拍卖机制的联盟组建算法。文献[15]提出了一种改进的核心法来组建联盟,实现了多Agent多任务分配和资源分配。然而MAS中资源可转移且无损耗的特点导致MAS中的联盟组建方法不能直接应用于多无人机联盟组建。MRS中虽然资源不可转移且是可损耗的,但是MRS中的联盟组建算法实时性不高,不适用于因飞行速度较快而对算法实时性要求很高的多无人机系统。
因此,设计实时性较高的且适用于未知环境下的异构多无人机联盟组建算法,以提高多无人机协同执行搜索打击任务时的效能,是一个值得研究的技术难点。本文针对这一问题进行研究。
1 问题描述
如图1所示,使用N架异构无人机对一片未知区域的M个静止目标执行搜索打击任务。这些无人机是异构的,体现在它们携带不同种类和数量的任务资源。每架无人机有唯一的编号Ai(i=1,2,…,N),其中无人机Ai携带有n种不同类型的任务资源(这些任务资源随着任务的执行而消耗),用当前资源向量表示:
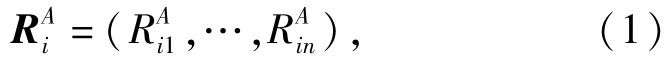

图1 多架异构无人机执行搜索打击任务示意图Fig.1 Schematic diagram of UAVs perfoming a search and attack mission
当多架无人机开始执行搜索打击任务时,目标的信息对于无人机来说是未知的,那么无人机需要以一定的搜索方式对任务区域展开搜索,在一定的探测距离内发现目标。假设无人机Ai发现目标Tj时,可以获知目标Tj的位置信息和资源信息。这里的资源信息指的是打击目标Tj所需的资源类型和数量,用资源需求向量表示:
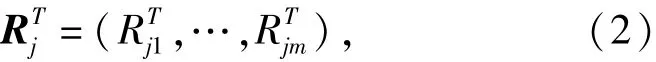
每架无人机均可以与其他各架无人机进行通信。如图1所示,当无人机Ai发现了目标Tj后,Ai成为联盟长机(CL)并将目标Tj的位置信息和资源信息广播给其他各架无人机,组建联盟完成对目标Tj的打击,这一过程称之为联盟组建提议。
对其他各架无人机而言,当接收到联盟组建提议消息后,对照自身所拥有的资源类型和数量,如果自身存在所需资源中的任何一种资源的话,就对Ai作出回应,将自身的最早到达时间(ETA)和当前资源向量反馈给无人机Ai.这一过程称之为联盟组建投标。其中Ak的最早到达时间ETA可由从其当前位置到目标位置的Dubins路径来确定,而作出回应的无人机Ak称之为潜在联盟成员(PCM).
联盟长机Ai接收到其他各架无人机的反馈信息后,其任务就是组建联盟。这一过程称之为联盟组建,构成联盟的无人机称之为联盟成员(CM).所组建的联盟需要满足以下约束和条件:1)为了缩短搜索打击任务的完成时间,要求在最短的时间内实现对目标的打击;2)要求联盟的规模最小,这是因为搜索打击任务的完成时间是由搜索时间和打击时间这两部分构成,若每次组建联盟时都使其规模最小,就可尽量使得更多的无人机参与对未知区域的搜索,在更短的时间内发现目标,从而缩短整个搜索打击任务的完成时间;3)为了对目标进行全方位打击,要求各个联盟成员同时对目标发起攻击;4)为了确保目标能被击毁,要求联盟中各联盟成员所拥有的资源总和满足打击需求。
无人机Ai发现了目标Tj时所组建的联盟记为,该联盟的资源向量(各联盟成员的当前资源向量之和)为表示所有的潜在联盟成员PCM和联盟长机CL所组成的集合,λk表示无人机Ak∈Λ的最早到达时间ETA,那么联盟组建问题可以描述为
2 联盟组建方法
2.1分阶次优联盟快速组建算法
由(3)式可以看出联盟组建问题是一个组合优化问题,随着无人机数量和目标数量的增加,该优化问题的求解将变得非常困难,因此,本文提出了一种分阶次优联盟快速组建算法(MSOCFA).
如图2所示,当无人机Ai发现了目标Tj时,Ai首先确定出打击目标Tj的资源需求向量如果无人机Ai的当前资源向量中并且无人机Ai不隶属于任何一个联盟,那么无人机Ai不需要组建联盟直接打击目标Tj;否则如果无人机Ai不能拥有打击目标Tj所需的全部资源,则成为联盟长机并将目标Tj的位置信息和资源信息广播给其他各架无人机。其他各架无人机Ak接收到联盟组建提议消息后,若自身处于“空闲”(即当前正在执行搜索任务)时,则对照自身所拥有的资源类型和数量,如果自身存在所需资源中的任何一种资源的话,就对联盟长机Ai作出回应,将自身的最早到达时间λk和当前资源向量反馈给联盟长机Ai.联盟长机Ai综合所有的反馈信息来组建联盟。如果联盟组建成功,就将联盟组建结果和整个联盟的最早到达时间发送给其他各架无人机;否则将联盟组建失败信息广播出去。最后,所组建联盟中的各个联盟成员需要根据整个联盟的最早到达时间重新规划各自的攻击路径(Dubins路径)以实现对目标的同时打击,而没有成为联盟成员的无人机则继续执行搜索任务。

图2 联盟快速组建过程示意图Fig.2 Flow chart of coalition formation process
在以上联盟快速组建过程中,联盟长机Ai采用MSOCFA决策出联盟MSOCFA主要分两个阶段:第1阶段,确定能够满足最短到达时间条件的所有无人机集合;第2阶段,裁剪第1阶段得到的集合以获得最小规模的联盟。MSOCFA两个阶段的伪代码分别如图3和图4所示。

图3 MSOCFA第1阶段伪代码Fig.3 Pseudo code of first stage of MSOCFA

图4 MSOCFA第2阶段伪代码Fig.4 Pseudo code of second stage of MSOCFA
在算法的第2阶段中,通过裁剪第1阶段得到的集合以获得最小规模的联盟。具体过程是,依次考察Cij中的每一架无人机,试探性地将无人机Aq从联盟中移除,如果移除无人机Aq后联盟的资源向量仍然满足打击目标所需的资源约束,那么就将无人机Aq从联盟中移除;否则,保留无人机Aq.循环结束后,就能得到最小规模的联盟Λ.
定理1 MSOCFA的第1阶段能够确定满足最短到达时间条件的无人机集合。
证明:设所有的潜在联盟成员和联盟长机构成集合Λ={A1,A2,…,AN′},相应地Λ中各架无人机的最早到达时间构成集合ETAs={λ1,λ2,…,λN′},并且假设在MSOCFA的第1阶段中,将ETAs中的元素按升序排列,假设排序后的结果为 Λu={λi1,λi2,…,λiN′},Λa={Ai1,Ai2,…,AiN′},并且 Λu中的元素满足性质 λik≤λik+1,∀k∈{1,…,N′-1}.对于任意的整数r∈{1,…,N′},令λir},那么的最短到达时间为λir.MSOCFA第1阶段的实质是找到最小的整数v∈{1,…,N′},使得是满足打击资源需求的无人机集合。既然中的元素是升序排列的,那么从中剔除任意一个非Aiv的元素,均不会改变无人机集合的最短到达时间λir,况且如果剔除Aiv后,无人机集合将不满足打击资源需求,因此是满足最短到达时间条件的无人机集合,定理1得证。
2.2冲突消解
2.2.1多架无人机同时侦察到同一目标
当多架无人机同时侦察到同一目标时,这些无人机均会发起联盟组建请求,导致资源竞争冲突,从而形成死锁。本文采用令牌机制来避免死锁,具体做法是:为每架无人机分配一个令牌数(i=1,2,…,N)来表征每架无人机的优先级,令牌数越大,无人机的优先级越高,那么优先成为联盟长机。
2.2.2一架无人机同时侦察到多个目标
当一架无人机同时侦察到多个目标时,该无人机无法为所侦察到的多个目标同时组建联盟,因此也产生冲突。此时需要为每个目标分配一个令牌数来表征打击每个目标的优先级(假设无人机侦察到目标时即可获知该目标的令牌数),令牌数越大,目标优先被打击。
2.2.3多架无人机同时侦察到多个目标
当多架无人机同时侦察到多个目标时,同样会因为同时发起联盟组建请求,而导致资源竞争冲突,形成死锁,此时需要综合应用无人机令牌数和目标的令牌数来消解冲突。例如,如果有4架无人机A1、A2、A3、A4搜索打击2个目标T1、T2,无人机令牌数的大小顺序为若A1侦察到T2的同时A4侦察到T1,A1和A4均成为联盟长机,这时候由于A1的优先级高于A4,那么A1优先组建联盟,此时A1作为长机,A2和 A3作为潜在联盟成员(A4已成为长机,故不作为潜在联盟成员),组建出联盟当联盟组建完毕后,A4才能组建联盟,此时潜在联盟成员集合为{A2},组建出联盟
值得注意的是还存在这样一种情况,若A1同时侦察到T1、T2,与此同时,A4也同时侦察到T1、T2.由于A1的优先级高于A4,那么A1优先组建联盟,此时A1作为长机,它需要在所发现的目标T1、T2中挑选出一个目标作为打击对象,由于T1的令牌数TNT1大于T2的令牌数,那么T1优先被打击,即首先由A1作为长机组建联盟完成对T1的打击,然后才让A4作为长机组建联盟完成对T2的打击。
2.3算法复杂度分析
为了说明MSOCFA具有较高的实时性,需要对其复杂度进行分析,提出如下定理2.
定理2 MSOCFA算法复杂度为O(N(lgN+ 2m)).
定理2说明MSOCFA是复杂度为O(N(lg N+ 2m))多项式时间算法,具有较低的计算复杂度,一般能够满足实时性要求[16]。
3 协同打击策略
多无人机同时打击问题在本质上是多无人机集结问题。针对这一问题,本文设计了一种同时打击策略来实现联盟成员对目标的同时打击。具体做法是:首先,当联盟组建完成后,联盟长机将各个联盟成员最早到达时间的最大值作为整个联盟的最早到达时间,并以通信的方式提供给联盟成员。然后,各个联盟成员根据整个联盟的最早到达时间,采用Dubins曲线原理来协同调整联盟成员各自的飞行路径,使得能够按照规定时间到达目标点。最后,各个联盟成员在路径跟踪算法的作用下沿着Dubins路径飞抵目标点,从而实现对目标的同时打击。该同时打击策略仅需要联盟长机将整个联盟的最早到达时间,以通信的方式一次性下达给联盟成员,不需要持续通信,从而减少了无人机之间的通信量,提高了隐蔽性。
3.1无人机数学模型
无人机安装有自动驾驶仪,其飞行速度和高度可以保持恒定。为了简化问题,假设无人机处于不同的飞行高度上,因此暂不考虑多无人机之间的碰撞问题,计划作为后续工作加以完善。在二维平面内,无人机的数学模型[17]为
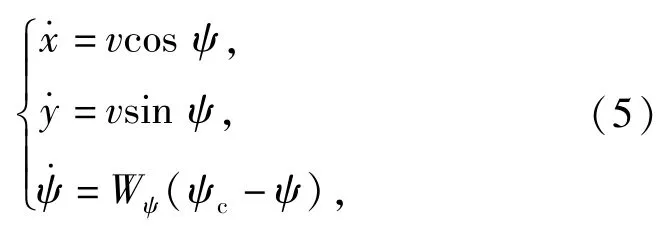
式中:v为无人机速度;Ψ∈[0,2π)为无人机的偏航角,按照东向为0,逆时针为正;WΨ为自动驾驶仪的增益;Ψc为偏航角制导指令,由路径跟踪制导律给出。
3.2基于Dubins曲线的协同路径规划方法
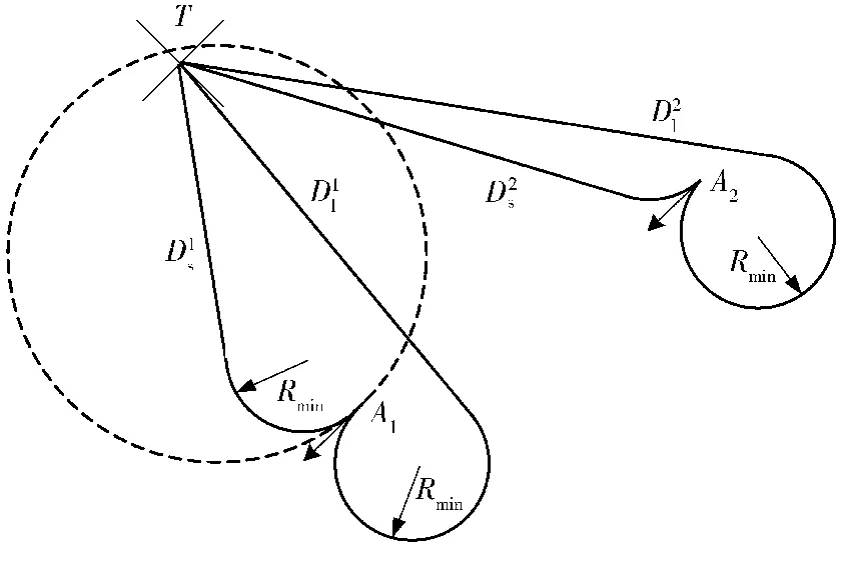
图5 基于Dubins曲线的协同路径规划示意图Fig.5 An example of selecting Dubins path
Dubins曲线[18]是由一段圆弧和一段直线构成,圆弧的半径r称之为Dubins曲线的半径。联盟成员通过调整各自的Dubins曲线的半径r来实现同时到达目标点。当给定无人机的位置和航向,沿Dubin曲线飞行有两种选择:1)Dubins较短路径(如图5中的Ds);2)Dubins较长路径(如图5中的Dl).本文选择Dubins较长路径Dl作为联盟成员抵达目标点的飞行路径,这是因为如果选择Dubins较短路径Ds会出现无法规划出抵达目标点的Dubins飞行路径的情况,该情况如图5所示。假设由无人机A1和A2构成联盟去打击目标T,如果选择Dubins较短路径Ds作为联盟成员A1和A2抵达目标点T的飞行路径,无人机A1需要按照增大Dubins曲线的半径r的方式来调整自身飞行路径的长度,使得但是随着半径r的增大,当目标T位于以r为半径的圆(图5中用虚线表示)的内部时,A1无法规划出抵达目标点的Dubins较短路径。此时,A1或许可以选择Dubins较长路径但是如果无论A1如何增大转弯半径r,均会使得从而无法规划出满足协同要求的路径。为了避免这种“路径长度不连续”情况的出现,本文选择Dubins较长路径Dl作为联盟成员抵达目标点的飞行路径,即无人机A1通过增大半径r,使得.另外考虑到无人机的飞行速度较快,要求路径规划算法具有较好的实时性,而采用一种单一规则的通用模型可以减少计算量,节省计算时间。故基于以上两点,本文统一采用Dubins较长路径Dl来规划到达目标点的路径。
3.3Dubins路径的跟踪制导控制
4 多无人机分布式自主协同控制策略
本文采用有限状态机(FSM)来实现多无人机分布式自主协同控制。多无人机协同执行搜索打击任务时,无人机存在着以下6种任务状态:1)搜索状态;2)联盟组建提议状态;3)联盟组建投标状态;4)联盟组建状态;5)Dubins路径规划状态;6)目标打击状态。这6种任务状态及其状态转移规则(I1~I11)如图6所示。
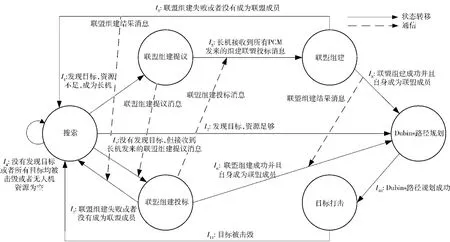
图6 无人机任务状态及其转移规则Fig.6 Mission state of UAV and its transition
4.1搜索状态
每架无人机的初始状态为搜索状态。当无人机处于搜索状态时,无人机以一种随机搜索的方式,对任务区域内的目标进行搜索。在随机搜索策略下,无人机在任务区域内一定角度沿直线飞行,到达搜索边界时,无人机以最小转弯半径转弯,进行边界规避,再次进入搜索区域,以一个新的角度继续沿直线飞行。无人机的边界规避策略可参考文献[20].若无人机发现目标Tj并且自身所拥有的任务资源不能完成对Tj的打击,就成为联盟长机(I1),进入联盟组建状态;如果自身所拥有的任务资源足够完成对Tj的打击(I2),就进入攻击路径规划状态。如果无人机没有发现目标,但接收到长机发来的联盟组建提议消息时(I3),该无人机成为潜在联盟成员,进入联盟组建投标状态。当无人机没有发现目标或者所有的目标均被击毁或者无人机的资源耗尽(I4)时,无人机处于搜索状态。
4.2联盟组建提议状态
联盟长机进入联盟组建提议状态后,将联盟组建提议消息广播给其他各架无人机。联盟组建提议消息主要包括目标Tj的位置信息和打击该目标所需的资源信息当联盟长机接收到所有潜在联盟成员发送的联盟组建投标消息时(I5),进入联盟组建状态。
4.3联盟组建投标状态
无人机进入联盟组建投标状态后,根据联盟长机发送的目标Tj的位置信息计算出自身的最早到达时间λk,并将联盟组建投标消息反馈给联盟长机Ai。联盟组建投标消息主要包括最早到达时间λk和当前资源向量之后无人机一直监听联盟长机Ai发送联盟组建结果。如果联盟组建成功并且该无人机成为联盟成员(I6),则进入攻击路径规划状态。如果联盟组建失败或者该无人机没有成为联盟成员(I7),则进入搜索状态。
4.4联盟组建状态
联盟长机进入联盟组建状态后,则综合所有的反馈信息来组建联盟,并将联盟组建结果消息反馈给所有的潜在联盟成员。联盟组建结果消息主要包括联盟组建是否成功、联盟成员编号集合、整个联盟的最早到达时间以及联盟的资源向量如果联盟组建成功并且联盟长机成为联盟成员(I8),则进入攻击路径规划状态。如果联盟组建失败或者联盟长机没有成为联盟成员(I9),则进入搜索状态。
4.5攻击路径规划状态
在攻击路径规划状态中,无人机需要根据整个联盟的最早到达时间重新规划各自的攻击路径以实现对目标的同时打击。当Dubins攻击路径规划完成后(I10),进入目标打击状态。
4.6目标打击状态
在目标打击状态中,无人机沿着各自规划出的Dubins攻击路径飞行,当到达目标点时,完成对目标的打击,相应地减少自身的资源。当目标被击毁时(I11),无人机重新进入搜索状态,回归“空闲”。
5 仿真结果与分析
首先,在5.1节中设置一个相对复杂的任务想定,来分析MSOCFA的合理性和可行性,同时来验证基于令牌数的冲突消解机制能够有效消解多架无人机协同执行搜索打击任务时,联盟组建过程中由于资源竞争所导致的冲突。其次,为了消除单次仿真的偶然性,更客观全面地评估任务完成的效果,在5.2节中,使用蒙特卡洛法分析无人机数量和目标数量对联盟组建的影响。然后,在未知环境中,除了要考虑目标出现位置的随机性外,还应考虑到目标出现时间的随机性,因此在5.3节中,设置目标的出现时间是随机的,来检验MSOCFA能否对随机出现的目标成功组建联盟。最后,在5.4节中,将MSOCFA与文献[21]中的PSO算法进行对比仿真,验证了MSOCFA具有较高的实时性,并且该对比仿真也说明,在平均任务完成率方面,MOCFA方法优于PSO方法。
5.1MSOCFA的仿真结果与分析
在仿真算例1中,任务区域设定为2 000m× 2 000m的矩形区域,区域内设定了3个目标,使用6架无人机执行搜索和打击任务。无人机的速度v=15m/s,最小转弯半径rmin=100 m,最大探测距离smax=300m,仿真步长设为0.1 s.无人机和目标的初始状态见表1和表2,算例1的结果如图7所示。
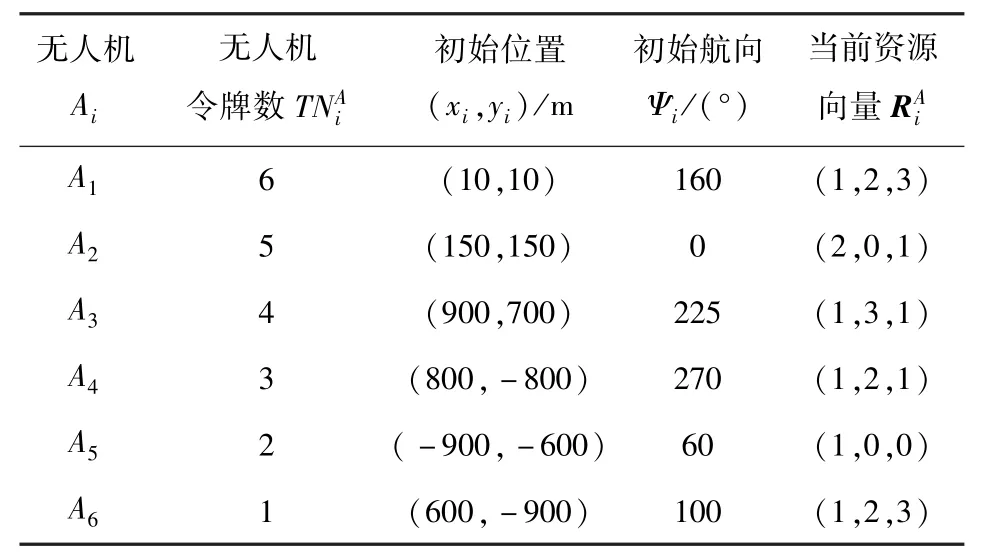
表1 无人机初始状态(算例1)Tab.1 Initial state of UAVs(Scenario 1)
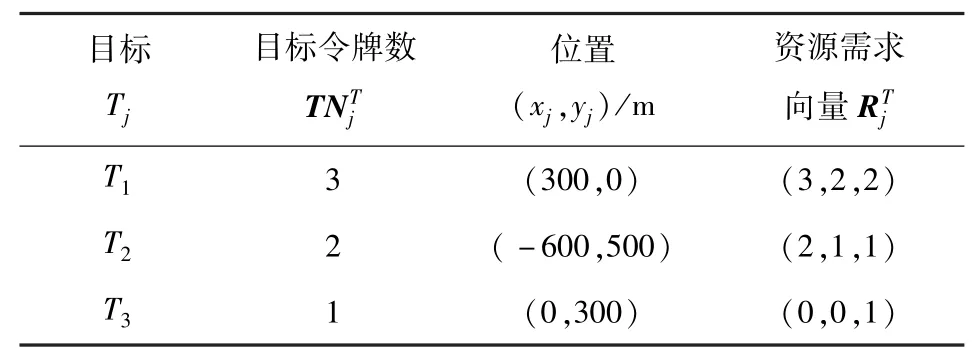
表2 目标初始状态(算例1)Tab.2 Initial state of targets(Scenario 1)
在t=0 s时,A1发现目标T1、T3的同时A2也发现了目标T1、T3,由于A1的令牌数比A2的令牌数大,那么A1优先组建联盟,此时A1作为长机,它需要在所发现的目标T1、T3中挑选出一个目标作为打击对象。又由于T1的令牌数大于T3的令牌数,那么目标T1优先被打击,即首先由A1作为长机组建联盟完成对目标T1的打击,将目标T1的信息发送给潜在联盟成员A3、A4、A5和A6(A1和A2这时候由于发现目标而成为了长机)。长机A1的联盟组建结果为其最早到达时间为105.3 s,其资源向量为(3,7,7),而打击目标T1的资源需求向量为(3,2,2),因此可以完成对目标T1的打击。

图7 6架无人机和3个目标的仿真结果(算例1)Fig.7 Simulation results of 6 UAVs and 3 targets(Scenario 1)
紧接着当A1完成联盟的组建后,A2才可以组建联盟,此时A2从它所发现的目标T1、T3中挑选一个作为打击对象,由于目标T1已经被分配,因此A2将目标T3作为打击对象。由于A2的当前资源向量,而打击目标T3的资源需求向量(0,0,1),也就是说A2拥有打击T3所需的全部资源,因此A2不需要组建联盟,直接完成对T3的打击,如图7所示,A2沿着规划出的Dubins路径飞抵目标T3,其最早到达时间为48.4 s.
在t=5.4 s时,A4发现了目标T2,A4成为长机,将目标T2的信息发送给潜在联盟成员A5(此时仅有A5是处于“空闲”的)。长机A4的联盟组建结果为,最早到达时间为112.9 s,其资源向量为(2,2,1),而打击T2的资源需求向量为(2,1,1),故可以完成对T2的打击。整个任务完成时间为119.3 s.整个过程中,联盟组建结果如表3所示。

表3 联盟组建结果(算例1)Tab.3 Results of coalition formation(Scenario 1)
上述仿真结果验证了MSOCFA的合理性和可行性,并且引入令牌机制后能有效消解多架无人机协同执行搜索打击任务时,联盟组建过程中由于资源竞争所导致的冲突。当多架无人机执行搜索打击任务时,发现目标后采用MSOCFA组建联盟,可以集中优势兵力在较短的时间内完成对目标的打击,并减少资源的浪费,提高了任务的执行效率。
5.2无人机数量和目标数量对MSOCFA的影响
为了进一步分析无人机数量和目标数量对MSOCFA的影响,消除单次仿真的偶然性,更客观、全面地评估任务完成的效果,按照Monte-Carlo法的思想,选取目标的数量为5、10和15,同时设定无人机的数量为5、10、15和20,分别进行12组实验。每组实验分别进行100次仿真,统计出每组实验的平均任务完成时间(AMCT)和平均任务完成率(APMC).任务完成率定义为:(击毁目标数/目标总数)×100%.
每次仿真中,任务区域、无人机的速度、最小转弯半径、最大探测距离和仿真步长与5.1中一致,同时设定最大仿真时间为t=1 000 s.目标的位置、无人机的初始位置和初始航向均是随机生成的。其中,在目标Tj的资源需求向量中,第q种资源(m=3)的数量为0~3内的随机整数;在无人机Ai的当前资源向量中,第p种资源(n=3)的数量为2~4之间的随机整数。每组实验的平均任务完成率和平均任务完成时间的统计结果分别如图8、图9所示。
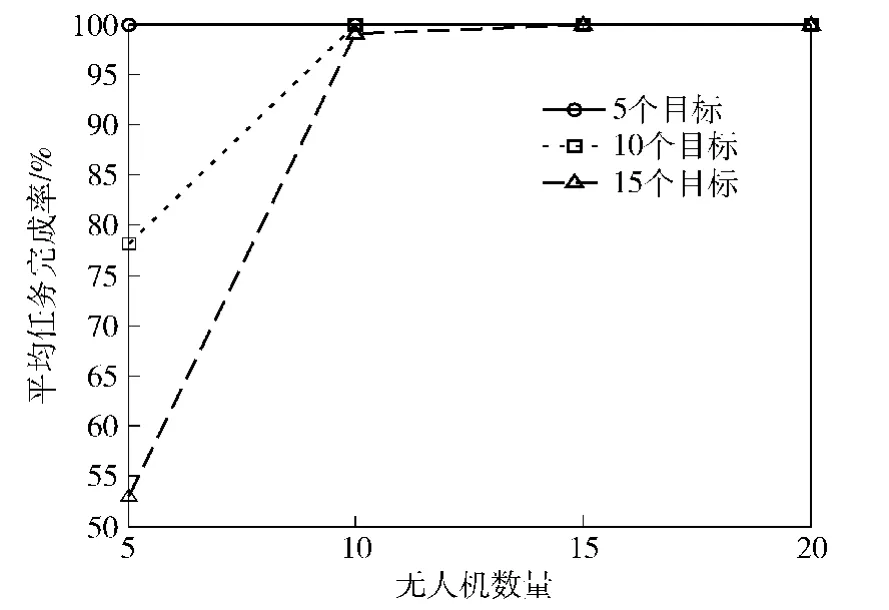
图8 不同无人机数量和目标数量下的平均任务完成率Fig.8 Comparison of averagemission completion rates
从统计结果可以看出:
1)当无人机数量一定时,目标数量越少,平均任务完成时间越短;
2)当目标数量一定时,无人机数量越多,平均任务完成时间越短;
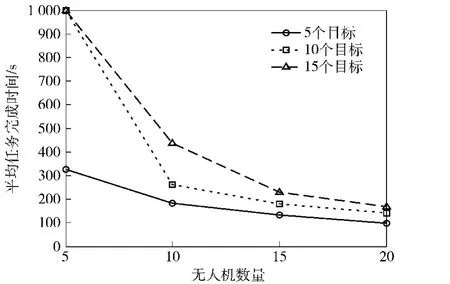
图9 不同无人机数量和目标数量下的平均任务完成时间Fig.9 Comparison of averagemission completion times
3)当无人机数量过少时,其平均任务完成率低于100%,其平均任务完成时间为1 000 s.这是因为在这种情况下,当无人机发现目标时,由于无人机的资源消耗殆尽,不能组建联盟完成对所发现目标的打击,而转入搜索状态,直到仿真结束,即t=1 000 s.例如当无人机的数量为5架,目标的数量为15个时,平均任务完成率仅为53%,平均任务完成时间为1 000 s.但随着无人机数量的增多,其资源也相应地增多,就能成功地组建联盟完成对所有目标的打击,因此其平均任务完成率逐渐增大,直至达到100%.其平均任务完成时间则会相应地减少,原因就在于随着无人机数量的增多,无人机发现目标所用的时间就越短,那么任务完成时间也就越短。
4)无人机和目标的数量和位置是随机生成的,可见MSOCFA算法对任意数量、任意位置的无人机和目标均有效。
5.3目标出现时间随机时的仿真结果与分析
在未知环境中,除了要考虑目标出现位置的随机性外,还应考虑到目标出现时间的随机性,因此需要设置目标的出现时间是随机的,来检验MSOCFA能否对随机出现的目标成功组建联盟。
在仿真算例2中,任务区域、无人机的速度、最小转弯半径、最大探测距离和仿真步长与5.1中一致,设置4架无人机搜索打击2个目标的任务想定,无人机和目标的初始状态见表4和表5,其中目标T1的出现时间是预先未知且是随机的。
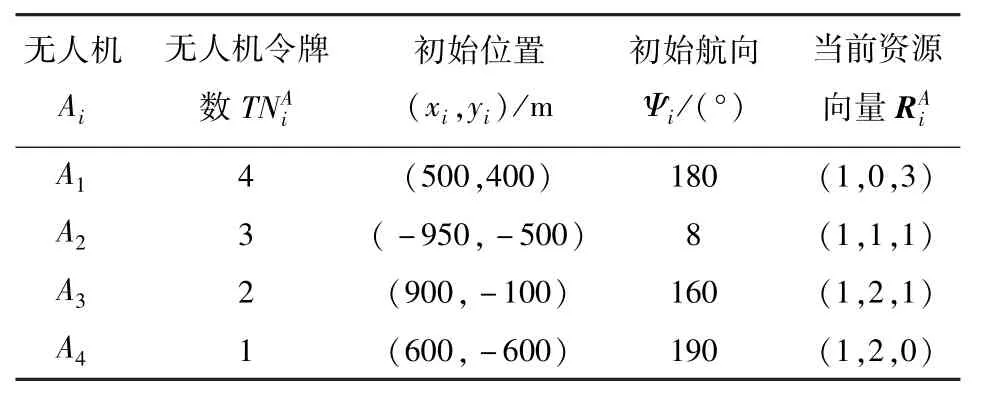
表4 无人机初始状态(算例2)Tab.4 Initial state of UAVs(Scenario 2)

表5 目标初始状态(算例2)Tab.5 Initial state of targets(Scenario 2)
如图10所示,在t=71.9 s时,A1发现T2,由于打击T2所需的资源向量为=(2,2,2),而A1的当前资源向量为=(1,0,3),A1没有足够的资源,因此成为联盟长机,组建联盟中的联盟成员为A1和A3,其最早到达时间为87.8 s,其资源向量为(2,2,4).打击完 T2后,A1的当前资源向量变为=(0,0,1),A3的当前资源向量变为=(0,0,1).

图10 t=71.9 s时,A1发现T2(算例2)Fig.10 A1detects T2for t=71.9 s(Scenario 2)
如图11所示,在t=172.0 s时,目标T1出现。在图12中,当t=172.3 s时,A2发现T1,由于打击T1所需的资源向量为=(2,3,2),而A2的当前资源向量为=(1,1,1),A2没有足够的资源,因此成为联盟长机,组建联盟中的联盟成员为A2、A3和A4,其最早到达时间为137.9 s,其资源向量为(2,3,2).打击完T1后,A2的当前资源向量变为=(0,0,0),A3的当前资源向量变为=(0,0,0),A4的当前资源向量变为=(0,0,0).整个任务完成时间为316.3 s.算例2的最终仿真结果如图13所示。
5.4MSOCFA与PSO的仿真对比
为了验证MSOCFA具有较高的实时性,将本文方法与文献[21]的PSO算法进行对比,重点考察任务完成时间与算法的时间开销。实验环境为Intel(R)Core(TM)Duo CPU,主频2.4GHz,内存为2 GB DDRII.仿真平台开发工具为Microsoft Visual C++6.0.在算例3中,采用4架无人机协同搜索打击4个目标,无人机和目标的初始状态分别如表6和表7所示。

图11 t=172.0 s时,目标T1出现(算例2)Fig.11 Target T1appears for t=172.0 s(Scenario 2)
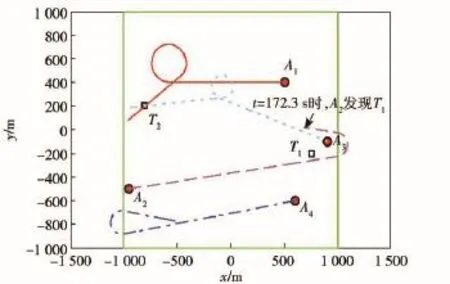
图12 t=172.3 s时,A2发现T1(算例2)Fig.12 A2detects T1for t=172.3 s(Scenario 2)

图13 4架无人机和2个目标的仿真结果(算例2)Fig.13 Simulation results of 4 UAVs and 2 targets(Scenario 2)

表6 无人机初始状态(算例3:MSOCFA与PSO仿真对比)Tab.6 The initial states of 4 UAVs in the comparison simulations using MSOCFA and PSO(Scenario 3)
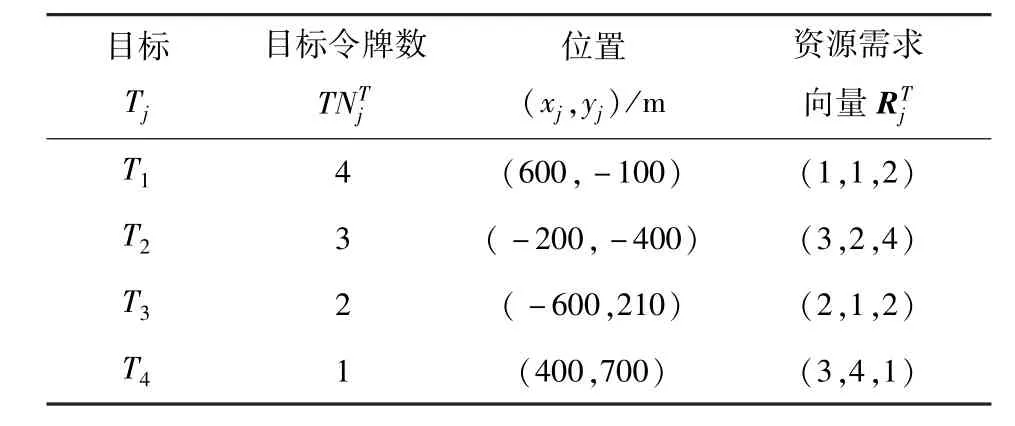
表7 目标初始状态(算例3:MSOCFA与PSO仿真对比)Tab.7 The initial states of target in the comparison simulations using MSOCFA and PSO(scenario 3)
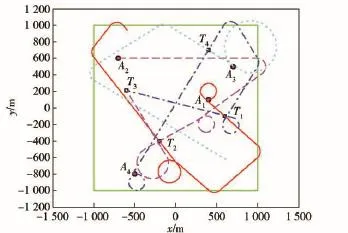
图14 采用MSOCFA的仿真结果Fig.14 Mission performance achieved using MSOCFA
图14为采用MSOCFA算法的仿真结果,当t= 0 s时,A1发现T1,由于A1的当前资源向量=(2,3,4),而打击T1的资源需求向量=(1,1,2),也就是说A1拥有打击T1所需的全部资源,因此A1不需要组建联盟,直接完成对T1的打击。当t=0.9 s时,A3发现T4成为长机,将T4的信息发送给潜在联盟成员A2、A4,建联盟,其最早到达时间为156.9 s.当t=190.3 s时,A1发现T2成为长机,将T2的信息发送给潜在联盟成员A2、A3、A4,建联盟=,其最早到达时间为81.9 s.当t=284.1 s时,A3发现T3成为长机,将T3的信息发送给潜在联盟成员A1、A2、A4,建联盟其最早到达时间为122.9 s.整个搜索打击任务的完成时间为406.5 s.MSOCFA算法给出的联盟组建结果如表8所示。

表8 采用MSOCFA时的联盟组建结果Tab.8 The details of coalition formation using MSOCFA
图15为采用PSO算法的仿真结果。表9给出了采用PSO求解得到的最优联盟组建结果,A1首先完成对T1的打击,然后与A4一起形成联盟完成对T4的打击。A2、A3分别打击T3、T2.整个任务的完成时间为157.4 s.

图15 采用PSO时的仿真结果Fig.15 Mission performance achieved using PSO

表9 采用PSO的联盟组建结果Tab.9 The details of coalition formation using PSO
MSOCFA与PSO的对比结果如表10所示,可以看出,在任务完成时间上,PSO优于MSOCFA,产生这一结果有两方面的原因:一方面,正如文献[21]所指出的,采用PSO求解联盟组建问题时,需要预先知道目标的数量、位置和打击目标所需的资源向量,因此无人机不需要对整个作战区域进行搜索,直接根据预先掌握的信息组建联盟完成对所有目标的打击。而采用MSOCFA不需要预先知道目标的数量、位置和打击目标所需的资源向量等信息,那么无人机需要对目标进行搜索,当发现目标时,才组建联盟。另一方面,PSO算法得到的是全局最优联盟组建方案,而MSOCFA为了提高算法的实时性,通过分阶段求解策略来降低问题的复杂程度。虽然MSOCFA得不到严格的全局最优解,但是其给出的联盟组建结果是合理和可行的。况且在算法时间开销方面,PSO算法的CPU计算时间为17.3 s,而MSOCFA的CPU计算时间为64 ms,因此在算法的实时性方面,MSOCFA明显优于PSO算法,从而验证了MSOCFA具有较高的实时性。
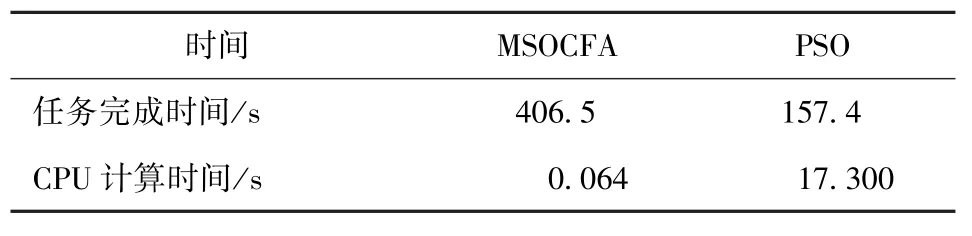
表10 MSOCFA与PSO的对比Tab.10 Comparison of MSOCFA and PSO
为了更为全面地比较MSOCFA与PSO这两种算法的性能,按照Monte-Carlo法的思想,选取目标的数量为10,同时设定无人机的数量为5、10、15和20,分别进行4组实验。每组实验分别进行100次仿真,统计出每组实验的平均任务完成率、平均任务完成时间、平均CPU计算时间。
每次仿真中,任务区域、无人机的速度、最小转弯半径、最大探测距离和仿真步长与5.1节一致,同时设定最大仿真时间为t=1 000 s.PSO算法的迭代次数为5 000次。目标的位置、无人机的初始位置和初始航向均是随机生成的。每组实验的平均任务完成率、平均任务完成时间、平均CPU计算时间的统计结果分别如图16~图19所示。
从统计结果可以看出:
1)在任务完成时间上,PSO优于MSOCFA,其原因在算例3中已做分析。
2)当无人机数量过少时(例如5架无人机搜索打击10个目标),PSO的任务完成率为0%,这是因为无人机的数量过少,无人机系统所有资源总和不足以完成对所有目标的打击,当采用PSO算法时,求解不出联盟组建问题的全局最优解,因而平均任务完成率为0%.
3)当无人机数量过少时(例如5架无人机搜索打击10个目标),尽管采用MSOCFA时的平均任务完成率也不能达到100%(这是因为无人机系统所有资源总和不足以完成对所有目标的打击),但是其平均任务完成率为78.2%,比基于PSO的联盟组建策略要高。这是因为,在MSOCFA算法中,当无人机发现目标时,才会动态地组建联盟,执行对该目标的打击,因此先前被发现的目标能被摧毁。但随着搜索打击任务的执行,无人机的资源消耗殆尽,不能组建联盟完成对后续发现目标的打击,而转入搜索状态,直到仿真结束。
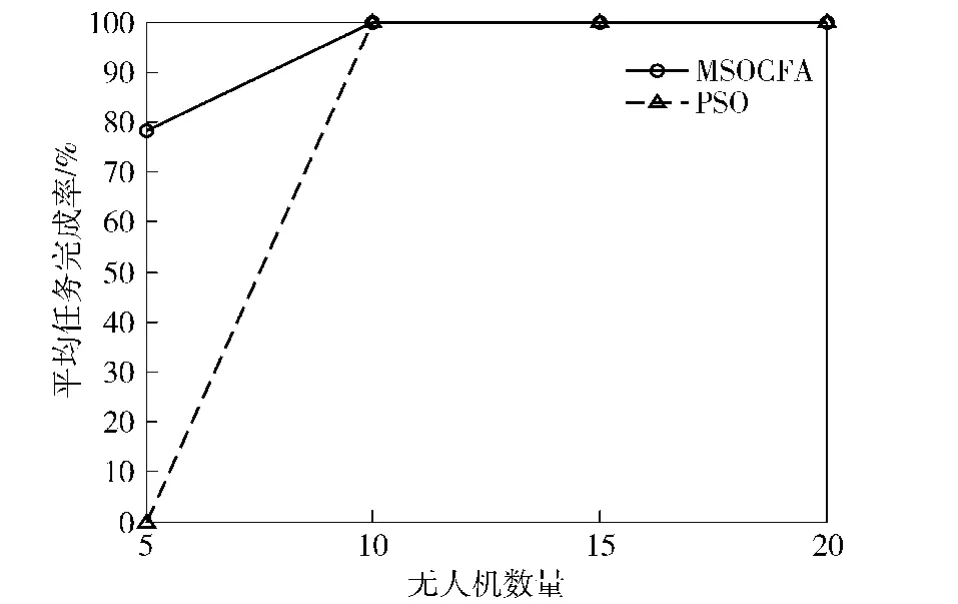
图16 不同联盟组建策略下的平均任务完成率(MSOCFA vs.PSO)Fig.16 Comparison of averagemission completion rates(MSOCFA vs.PSO)
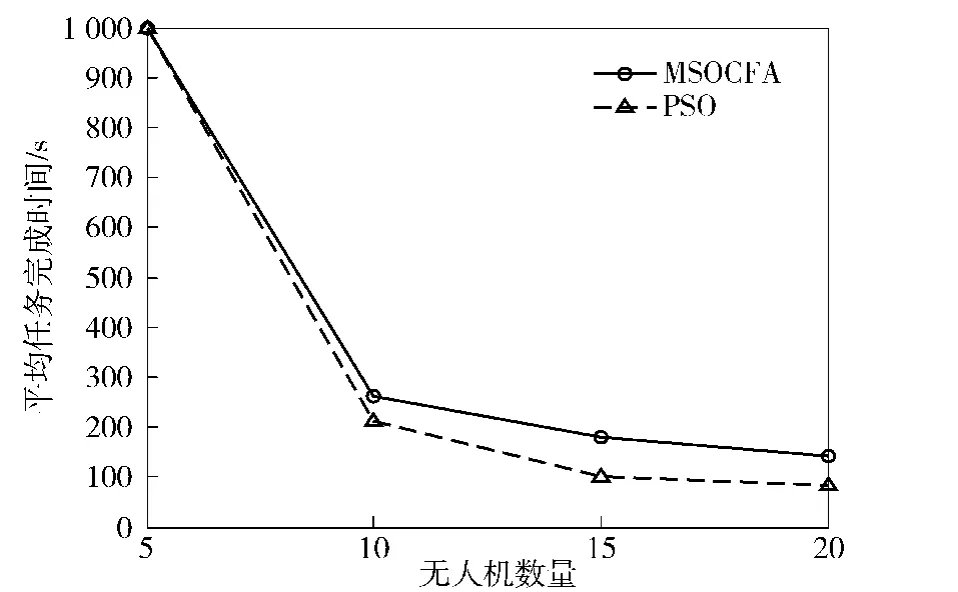
图17 不同联盟组建策略下的平均任务完成时间(MSOCFA vs.PSO)Fig.17 Comparison of averagemission completion times(MSOCFA vs.PSO)
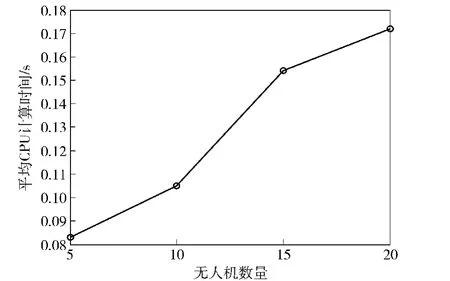
图18 MSOCFA算法的平均CPU计算时间Fig.18 Mean time taken to complete a simulation using MSOCFA
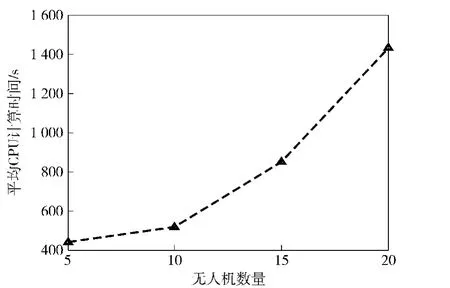
图19 PSO算法的平均CPU计算时间Fig.19 Mean time taken to complete a simulation using PSO
4)随着无人机数量的增多,PSO的CPU计算时间呈指数增长,虽然MSOCFA的CPU计算时间也随着无人机数量的增加而增长,但是不同于PSO算法,并不呈指数形式增长,其增长得较为缓慢。并且当无人机数量为5、10、15、20时,MSOCFA算法的CPU计算时间均远小于 PSO算法,由此可见,MSOCFA的实时性明显高于PSO算法。
上述Monte Carlo仿真对比实验说明:任务完成率与所采用的联盟组建策略是有关系的,在平均任务完成率方面,MOCFA方法优于 PSO方法;MSOCFA算法比PSO算法具有较高的实时性。
6 结论
本文借鉴联盟的思想来解决未知环境下异构多无人机协同搜索打击时的任务分配问题。得到了如下结论:
1)提出以最小化目标打击时间和最小化联盟规模为优化指标,以同时打击和满足打击资源需求为约束条件的联盟组建模型。该模型适用于解决异构多无人机在未知环境下协同执行搜索打击任务时的任务分配问题。
2)由于联盟组建问题是一个组合优化问题,提出了分阶次优联盟快速组建算法MSOCFA.算法复杂度分析证明了该算法是一个多项式时间算法,能够满足实时性要求,并且通过与PSO算法进行仿真对比也验证了该算法具有较高的实时性。另外对比仿真也说明,在平均任务完成率方面,MSOCFA方法优于PSO方法。
3)使用多次仿真统计了不同无人机数量和不同目标数量下的平均任务完成率和平均任务完成时间,验证了无人机数量和目标数量对联盟组建的影响,即无人机数量越多,目标数量越少,其平均任务完成时间越短;但是当无人机数量过少时,其平均任务完成率低于100%,其原因在于无人机的资源不足,无法组建出联盟完成对所发现目标的打击。
4)在本文中,没有考虑诸如通信距离、通信时延等通信约束对联盟组建的影响,所以还需考虑无人机之间的通信约束条件,对联盟组建方法作进一步完善。除此之外,后续工作还需要针对无人机之间的避撞问题问题,进一步研究无人机的感知与规避技术,以保证无人机的飞行安全。
(References)
[1]Shima T,Rasmussen S.UAV cooperative decision and control challenges and practical approaches[M].Philadelphia:Society for industrial and Applied Mathematics,2009.
[2]Schumacher C,Chandler PR,Rasmussen SR.Task allocation for wide area searchmunitions via network flow optimization[C]∥AIAA Guidance,Navigation,and Control Conference and Exhibit.Montreal,QC:AIAA,2001.
[3]Schumacher C,Chandler P R,Rasmussen S R.Task allocation for wide area search munitions via iterative network flow[C]∥AIAA Guidance,Navigation,and Control Conference and Exhibit. Monterey,CA:AIAA,2002.
[4]Schumacher C,Chandler P R,Pachter M,et al.UAV task assignmentwith timing constrains[C]∥AIAA Guidance,Navigation,and Control Conference and Exhibit.Austin,Texas:AIAA,2003.
[5]Schumacher C,Chandler P R,Pachter M,et al.UAV task assignmentwith timing constrains via mixed integer linear programming[C]∥AIAA 3rd Unmanned Unlimited Technical Conference,Workshop and Exhibit.Chicago,Illinois:AIAA,2004.
[6]Schumacher C,Chandler PR,Pachter M,et al.Constrained optimization for UAV task assignment[C]∥AIAA Guidance,Navigation,and Control Conference and Exhibit.Providence,RI:AIAA,2004.
[7]Darrah M A,Niland W M,Stolarik BM.Multiple UAV dynamic task allocation usingmixed integer linear programming in a SEAD mission[C]∥AIAA InfoTech at Aerospace:Advancing Contemporary Aerospace Technologies and Their Integration.Arlington,VA:AIAA,2005.
[8]Alighanbari M,How JP.Decentralized task assignment for unmanned aerial vehicles[C]∥Proceedings of the44th IEEEConference on Decision and Control,and the European Control Conference.Seville,Spain:IEEE,2005:5668-5673.
[9]Shima T,Rasmussen SJ,Sparks A G,etal.Multiple task assignments for cooperating uninhabited aerial vehicles using genetic algorithms[J].Computers&Operations Research,2006,33(11):3252-3269.
[10]钱艳平,夏洁,刘天宇.基于合同网的无人机协同目标分配方法[J].系统仿真学报,2011,23(8):1672-1676. QIAN Yan-ping,XIA jie,LIU Tian-yu.Task assignment scheme based on contract net[J].Journal of System Simulation,2011,23(8):1672-1676.(in Chinese)
[11]廖沫,陈宗基.基于满意决策的多机协同目标分配算法[J].北京航空航天大学学报,2007,33(1):81-85. LIAO Mo,CHEN Zong-ji.Coordinated target assignment in multi-UAV based on satisficing decision theory[J].Journal of Beijing Universityof Aeronautics andAstronautics,2007,33(1):81-85.(in Chinese)
[12]Shehory O,Kraus S.Methods for task allocation via agent coalition formation[J].Artificial Intelligence,1998,101(1/2):165-200.
[13]Service T C,Adams JA.Coalition formation for task allocation:theory and algorithms[J].Autonomous Agents and Multi-Agent Systems,2011,22(2):225-248.
[14]Vig L,Adams JA.Multi-robot coalition formation[J].IEEE Transactions on Robotics,2006,22(4):637-649.
[15]Chalkiadakis G,Markakis E,Boutilier C.Coalition formation under uncertainty:bargaining equilibria and the Bayesian core stability concept[C]∥Proceedings of the6th International Joint Conference on Autonomous Agents&Multiagent System.Honolulu,HI:the Association for Computing Machinery,2007:412-419.
[16]Cormen TH,Leiserson C E,Rivest R L.Introduction to algorithms[M].3rd ed.New York:MIT Press,2009.
[17]Nelson D R,Barber D B,McLain TW,et al.Vector field path following for miniature air vehicles[J].IEEE Transactions on Robotics,2007,23(3):519-529.
[18]Tsourdos A,White B,Shanmugavel M.Cooperative path planning of unmanned aerial vehicles[M].Bognor Regis:John Wiley and Sons Ltd,2011.
[19]Ambrosino G,Ariola M,Ciniglio F,et al.Path generation and tracking in 3-D for UAVs[J].IEEE Transactions on Control Systems Technology,2009,17(4):980-988.
[20]符小卫,李建,高晓光.带通信约束的多无人机协同搜索中的目标分配[J].航空学报,2014,35(5):1347-1356. FU Xiao-wei,LI Jian,GAO Xiao-guang.Target allocation in multi-UAV cooperative search with communication constraints [J].Acta Aeronautica et Astronautica Sinica,2014,35(5):1347-1356.(in Chinese)
[21]Sujit P B,Georget JM,Beard R.Multiple UAV task allocation using particle swarm optimization[C]∥AIAA Guidance,Navigation and Control Conference and Exhibit.Honolulu,HI:AIAA,2008.
Coalition Formation of Multiple Heterogeneous Unmanned Aerial Vehicles in Cooperative Search and Attack in Unknown Environment
LIU Zhong1,GAO Xiao-guang1,FU Xiao-wei1,MOU Zhi-ying2
(1.School of Electronics and Information,Northwestern Polytechnical University,Xi'an 710129,Shaanxi,China;2.Science and Technology on Avionics Integration Laboratory,Shanghai200233,China)
A novelmethod for coalition formation ofmultiple heterogeneous unmanned aerial vehicles in cooperative search and attack in unknown environment is presented to improve the cooperative search and attack effectivenesses ofmultiple heterogeneous unmanned aerial vehicles.A coalition formation model is established based on theminimum target attack time and theminimum coalition scalewith the constraints of required resources and simultaneous strike.A multistage sub-optimal coalition formation algorithm (MSOCFA)that has low computational complexity is proposed to solve the optimization problem of coalition formation.The performances ofMSOCFA and partical swarm optimization algorithms are compared in terms ofmission performance,complexity of algorithm and time taken to form the coalitions.In order to enable themultiple cooperative unmanned aerial vehicles to accomplish the search and attack missions autonomously,a distributed autonomous control strategy is proposed,which is based on the finite-statemachine(FSM).The simulation results show the rationality,validity and high real-time performance of the proposed method for the coalition formation ofmultiple heterogeneous unmanned aerial vehicles in cooperative search and attack in the unknown environment.Monte Carlomethod is employed to validate the impact of the number of unmanned aerial vehicles and targets on coalition formation.The reduced average mission completion time relates to the decreased number of targets and the increased the number of unmanned aerial vehicles.
control science and technology;multi-unmanned aerial vehicle;cooperative search and prosecute;coalition formation;finite-statemachine;Monte Carlomethod
V 279
A
1000-1093(2015)12-2284-14
10.3969/j.issn.1000-1093.2015.12.011
2014-12-15
航空科学基金、航空电子系统综合技术重点实验室联合项目(20155553041);中央高校基本科研业务费专项资金项目(3102015ZY092)
刘重(1985—),男,博士研究生。E-mail:15829732829@163.com;高晓光(1957—),女,教授,博士生导师。E-mail:xggao@nwpu.edu.cn
