非均质底水油藏水平井ICD完井耦合模型与目标剖面计算方法
2015-09-26李根生崔明月黄中伟梁月松中国石油大学油气资源与探测国家重点实验室北京049中国石油勘探开发研究院廊坊分院河北廊坊065007
付 宣 李根生 崔明月 黄中伟 梁月松(.中国石油大学油气资源与探测国家重点实验室,北京 049;.中国石油勘探开发研究院廊坊分院,河北廊坊 065007)
非均质底水油藏水平井ICD完井耦合模型与目标剖面计算方法
付宣1李根生1崔明月2黄中伟1梁月松1
(1.中国石油大学油气资源与探测国家重点实验室,北京102249;2.中国石油勘探开发研究院廊坊分院,河北廊坊065007)
入流控制装置(Inflow Control Device,ICD)近年来在水平井分段完井中应用日益广泛,但目前针对ICD完井建立的半解析耦合模型无法准确反映水平井端部效应,在ICD优化设计过程中对于目标入流剖面的选择缺乏依据。为此,首先引入了基于势的叠加原理和镜像反射原理的油藏渗流模型用以准确反映水平井入流特征,建立了适用于非均质底水油藏水平井ICD完井的稳态耦合模型;之后考虑油井不同的生产制度,给出了非均质油藏水平井ICD完井优化目标入流剖面的确定方法,并以喷嘴型ICD为例对ICD设计流程进行了具体描述,对最优非均匀ICD和最优均匀ICD计算结果进行了对比分析。结果表明:ICD优化设计与生产制度有很大关系,均匀入流剖面并非总是理想的入流剖面;非均匀ICD控流效果要优于均匀ICD,但均匀ICD完井对井底流压有较宽的适应性;高生产压差有助于发挥喷嘴型ICD的控流优势。
非均质;底水油藏;ICD;耦合模型;目标剖面
入流控制装置(ICD)完井是20世纪90年代末发展起来的一种高级完井方式,通过引入额外压降来均衡沿水平井筒的入流剖面,延缓水气突破时间,目前已成为解决由于水平井跟趾效应和油藏非均质性所带来的各类生产问题的有效手段[1-3]。
ICD完井优化涉及油藏、井筒和ICD装置3个方面流动的耦合问题,对于非均质油藏,多采用油藏数值模拟器对ICD进行完井设计。目前流行的油藏模拟器均集成了ICD压降计算模型[4-7],但普遍缺乏优化算法,使用者需要手工调整ICD参数来制定完井方案,工作效率较低。近年来,一些研究者提出采用半解析模型对ICD进行快速优化设计[8-9],一般采用解析的产能指数公式对各段入流量进行计算,但是对于非均质油藏,水平井各段产能指数难以确定,该方法忽略了水平井端部效应,即跟趾两端入流量较大这一事实,实际生产情况存在偏差,影响ICD完井优化设计结果。
在ICD设计实践中,普遍认为依据水平井渗透率分布进行非均匀参数设计能够取得更好的控流效果[10],即对高渗段采用高强度ICD、对低渗段采用低强度ICD,或者不加入ICD甚至关闭井段;当渗透率分布并不确定时,则建议采用各段均匀ICD完井,以降低渗透率不确定性带来的设计失误[11]。但无论是均匀ICD还是非均匀ICD完井设计,其首要任务均是要确定目标入流剖面,并在此基础上获得目标ICD压降,然后对各段进行参数选择。一般认为均匀入流剖面应当作为目标入流剖面,但事实上目标入流剖面的选择与生产制度有很大关系,尤其受井底流压影响最为明显,但目前针对不同生产制度下ICD完井最佳入流剖面应当如何选择尚无学者给出具体建议。
建立适用于非均质底水油藏水平井ICD完井设计的半解析耦合流动模型,渗流部分采用基于势的叠加和镜像反射原理的稳态渗流模型,能较好地反映水平井的端部效应。模型在段内考虑了表皮影响,在段间引入等效渗透率,有效反映沿水平井筒的非均质特性。针对目标入流剖面的选择展开讨论,详细阐述在定压生产和定产生产2种生产模式下目标入流剖面的确定方法,给出优化设计流程,并以喷嘴型ICD为例对设计流程进行了具体描述,对最优非均匀ICD和最优均匀ICD计算结果进行对比分析。
1 ICD完井油藏井筒耦合模型
1.1油藏渗流模型
采用基于势的叠加原理和镜像反射原理的油藏渗流模型,引入等效渗透率来反应水平井各段的非均质性。该模型能反映水平井各段间的相互干扰,在均质油藏情况下可以反映出水平井U型入流剖面的特性,并且易于编程,适用于多种油藏类型的渗流计算。
假设油藏为底水油藏,水平井平行于油水边界,把长度为L的水平井分成N段,依据镜像反映和势的叠加原理,考虑各段表皮系数可得油藏渗流方程为

即
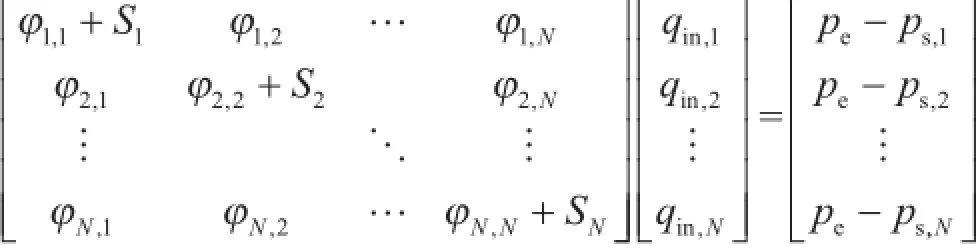
式中,S为各段表皮系数,pe为油层边界或泄油边界压力,ps,j为第j水平段沙面处压力值,qin,j为第j段水平段入流量。φi,j依据油藏类型可修改为不同形式[12],其中底水油藏表达式为
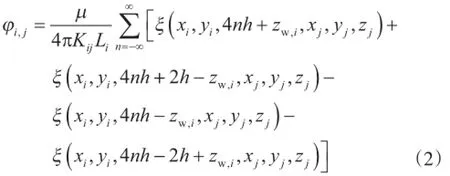
式中,n为镜像反射次数,Li为第i段水平段的长度,Ki,j为第i段到第j段的等效渗透率,可由下式计算得到[13]
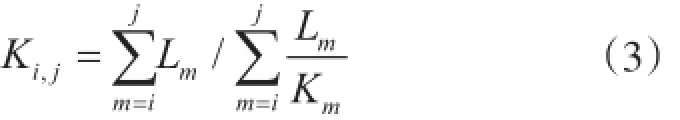
1.2水平井筒压降模型
水平井油管内压降计算模型如下(忽略重力压降)[14]

即

式中,fj为第j段摩擦因数,pt,j为第j段油管内压力,qin,j为第j段进入油管的入流量,qw,j为第j段微元管内流量。油管压力分布的边界条件为

式中,pwf为跟端油管内压力,即井底流压。
1.3ICD压降模型
采用喷嘴/孔眼型ICD,压降主要由节流产生,计算公式如下[15]

式中,qin,j为第j段水平段入流量,dj为第j段水平段ICD喷嘴直径,nj为第j段水平段喷嘴数量,ρ为流体密度,CD为ICD流量系数,由实验测得。
1.4耦合流动模型
对于ICD完井,第j段油藏流动在沙面处压力与油管内压力相差一个ICD引入的附加压降,即

耦合模型求解流程如图 1所示。
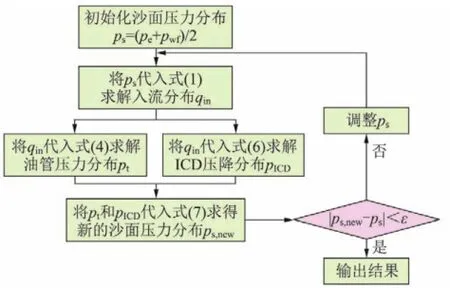
图1 ICD完井耦合模型求解流程
在定产条件下,每次压力分布收敛之后还需要判定产量是否收敛,如不收敛则需要重新调整井底流压pwf来初始化沙面压力,直到压力与产量均收敛为止。此耦合模型也可用于计算裸眼完井的入流剖面,只需将各段ICD压降设为0即可。
2 ICD完井优化设计
2.1目标入流剖面的确定方法
假设一口水平井完全以均匀入流剖面进行生产,油水界面均匀抬升,各段将同时见水,此时采收率为最大。但均匀入流剖面是否能够实现,取决于井底流压的设置,如果井底流压较高,且水平段存在较低渗透率分布时,均匀入流剖面将无法实现,因此均匀入流剖面并不一定在任何情况下可以当作最佳入流剖面,需要依生产情况进行调整。以定压生产和定产2种生产模式为例,详细叙述目标入流剖面的确定方法。
2.1.1定压生产定压条件下,如果在水平井中加入ICD,虽然可以延长水气突破时间,但是以牺牲日产量为代价的。如果水平井各段均按照裸眼井入流剖面中的最小值进行均匀生产,则水气突破时的累积产量可以达到最大,但是日产量过低,无法满足配产要求。因此在定压生产的条件下,还需要额外增加一个限制条件来进行目标剖面选择,即见水时间(或无水生产期)。当给定见水时间,则可计算出满足该时间的入流剖面值qm。底水油藏水平井见水时间与产量关系式如下[16]
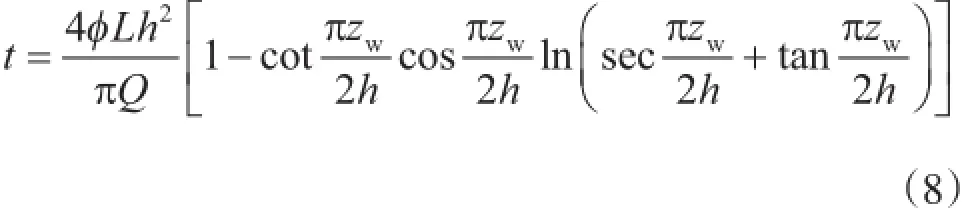
得到qm之后可按照以下步骤确定目标剖面:(1)计算裸眼完井定压生产入流剖面;(2)调整裸眼完井入流剖面,高于qm的各段流速下调至qm,低于qm各段流速保持不变,此时的入流剖面即为目标入流剖面。
经过以上步骤之后,目标入流剖面可能并非均匀分布,这种情况主要出现在井底流压较高时,此时一些特低渗井段即使在不安装ICD的情况下也无法使入流量高于qm。
2.1.2定日产量生产定产条件下,可用日产量除以水平井长度得到的均匀入流剖面作为目标剖面,该剖面既能满足日产量要求,又可以确保水气突破前最大的扫油面积,使累积产量最大化。但此时井底流压是一个不确定值,如果该值选择过高,则可能出现定压生产中的情况,即在不安装ICD的情况下也无法使一些低渗水平段的入流量高于目标剖面值,日产量要求无法满足;如果该值选择过低,有可能使原油无法自然产出地面,需要增加额外举升手段进行生产,增加了完井成本。因此,井底流压应当有一个合理的取值范围,确定方法如下。
(1)计算使得裸眼完井各段入流剖面均不低于目标剖面的井底流压pa。
(2)以保证油气顺利采出为原则,根据油气密度、黏度、井深、油管类型以及地面是否采取人工举升等因素,得到井底流压pb,该值应当确保小于pa,如果大于pa,则需要提高pa取值,此时目标剖面可能也已不再为均匀分布,需要适当考虑是否有一些段渗透率过低,需要关闭。
最后在以上取值范围[pb, pa]内选择若干井底流压,得出多组最优ICD完井方案,并对各方案入流剖面、见水时间以及日产量进行对比,选出最优完井方案。
2.2ICD参数优化设计流程
如果ICD可变参数较多,则可考虑固定一些次要参数,仅对某些主要参数进行优选见图2;如果水平井分段较多,且各参数取值范围较大,则可采用优化算法(如遗传算法)对ICD参数组合进行优选(注意这可能使得出来的值不是全局最优,而是局部最优),或者全井段采用均匀ICD完井,以减少程序计算量。优化的基本原则是尽量减少分段和ICD可变参数数量与取值,综合考虑完井成本和完井工具的设计精度,力求降低完井复杂性。

图2 ICD优化设计流程
2.3实例计算
下面通过实际算例来具体说明非均质底水油藏ICD完井的最优化过程,为简化计算,忽略沿井筒表皮因数的影响,并假设井筒内各处摩擦因数相等,ICD喷嘴流量系数为定值,假设为1。
油藏井筒基础数据见表 1。

表1 油藏井筒基础数据
假设井筒平均分为10段,每段50 m,渗透率沿井筒分布见表 2。

表2 完井段渗透率分布
喷嘴直径调节范围2~8 mm,调节精度为1 mm;喷嘴数量调节范围1~8个,调节精度为1。
2.3.1定压生产假设井底流压要求为28 MPa,无水生产期要求为300 d。首先依据式(8)得各段最大入流速度为1.96 m3/d/m,之后依据图 1的计算流程得出裸眼完井时各段入流速度并将大于1.96 m3/d/m的各段入流速度改为1.96 m3/d/m,即得到定压条件下的目标入流剖面(表 3),不难看出,此时的目标入流剖面并不是均匀入流剖面,部分低渗段的入流值小于1.96 m3/d/m。

表3 定压条件下目标入流剖面
依据图 2的ICD最优算法,得到最佳变参数ICD与最佳均匀ICD(3 mm×5)完井结果如图 3和表 4所示。
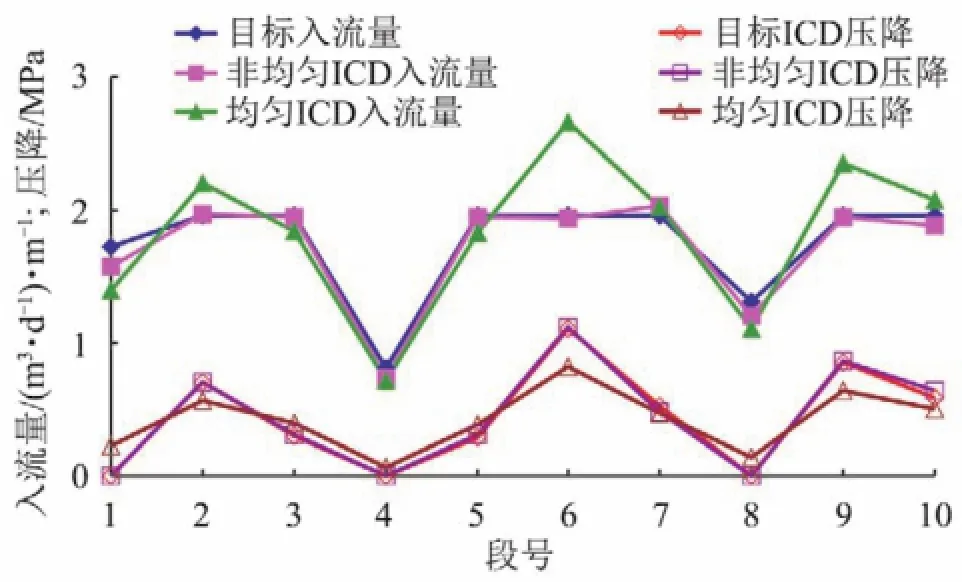
图3 定压条件下经优化后入流剖面和ICD压降分布
由以上结果可以看出,非均匀最优ICD完井方案显然优于均匀最优ICD方案,从图 3分析可知,非均匀ICD方案在高渗段的控流强度较大(第2,6,9段),使得各段入流剖面与目标剖面几乎重合,而均匀ICD方案各段的ICD参数相同,在高渗段区域产生的压降不足,导致这些段入流量较大,虽然日产量较高,但与要求的见水时间相差较大(表 4),综合评价,采用非均匀ICD完井,控流效果要好优于均匀ICD。
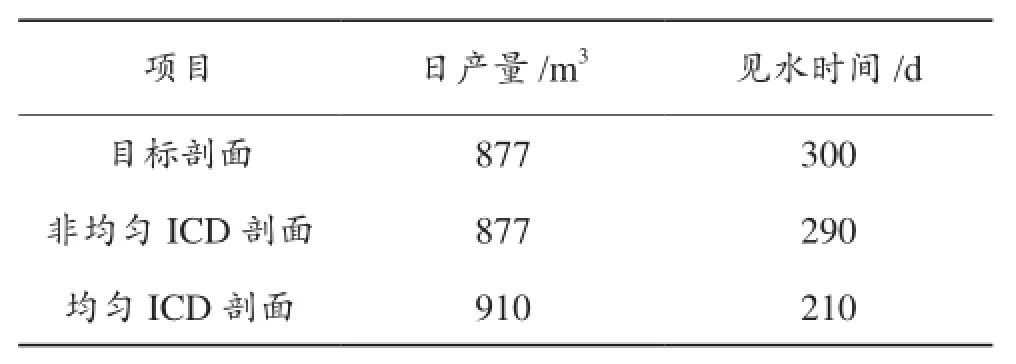
表4 定压条件下各完井方案日产量及见水时间
2.3.2定产生产假设油井要求日产量为800 m3,无人工举升自然采出。忽略油管尺寸变化以及原油脱气等因素,仅考虑流体重力和油管摩擦阻力影响,得到井底流压为18 MPa时,可保证油井按照800 m3/ d的产量顺利采出。依据日产量要求,目标入流剖面为各段1.6 m3/d/m。通过试算,如果采用裸眼完井,当井底流压不高于26 MPa时,各段入流值均可大于1.6 m3/d/m。由此井底流压范围为18~26 MPa。分别取井底流压为20 MPa,22 MPa和24 MPa进行均匀ICD和非均匀ICD优化设计,优化结果如图 4和表5所示。
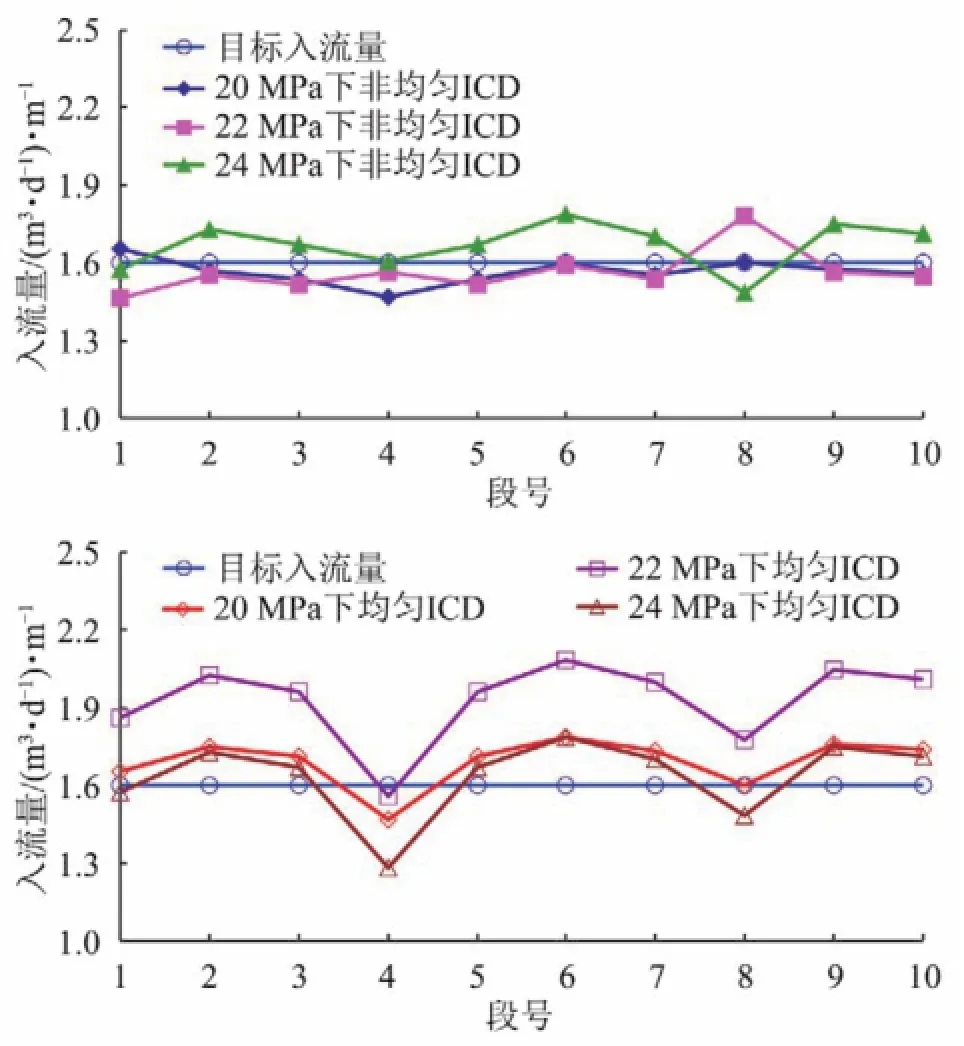
图4 定产条件下非均匀ICD入流剖面(上)和均匀ICD入流剖面(下)
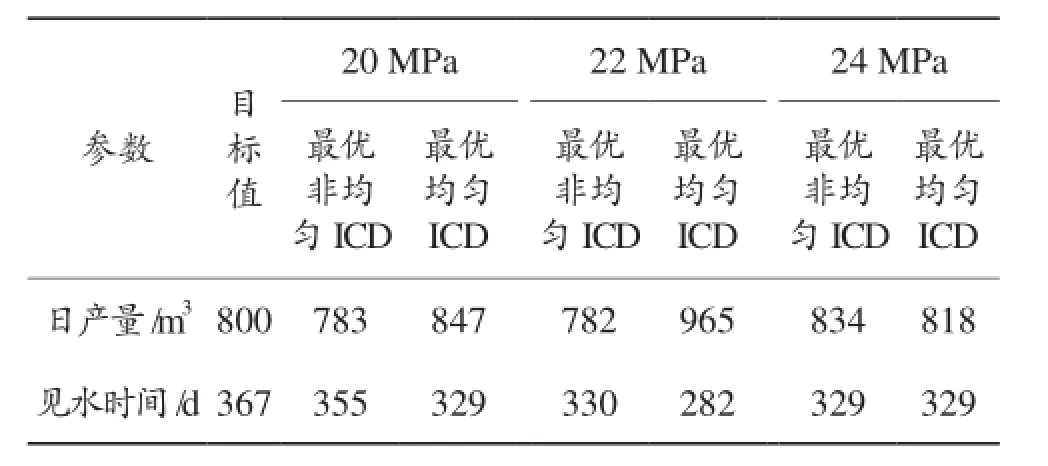
表5 定产条件下各完井方案日产量及见水时间
与定压生产情况相同,定产生产时,不同井底流压下,最优非均匀ICD完井方案的入流剖面均要好于均匀ICD完井方案,这是因为非均匀ICD是在各段分别选取最接近目标压降的参数组合,调节精度较高,而均匀ICD是在全井段选取最接近目标压降的ICD参数组合的,调节精度较低,对一些特高或特低渗段的调控能力有限。
无论是最优非均匀ICD完井还是最优均匀ICD完井,井底流压为20 MPa时的完井方案时,其入流剖面均最接近于目标入流剖面,这是因为由于喷嘴型ICD对于流速变化十分敏感,当生产压差增大时,入流速度上升,ICD产生的压降越大。一般认为当ICD压降大于等于油藏到沙面的压差时,控流效果最佳[17-18],从图 5可以看出,当井底压力在20 MPa时,所有段的ICD压降超过5 MPa,因此控流效果较好,而22 MPa和24 MPa时,低渗段(第4段)的ICD压降分别小于4 MPa和3 MPa。
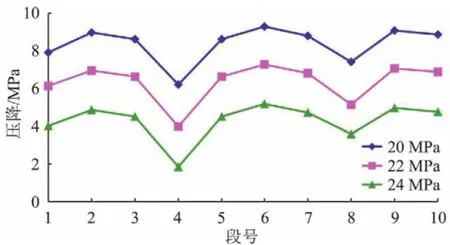
图5 定产条件下非均匀ICD压降分布
需要指出的是,对于22 MPa和24 MPa两种情况下,算法给出的均匀ICD最优方案均为2 mm×3(20 MPa时的均匀ICD最优方案为3 mm×1),由于本身ICD参数可取范围限制(喷嘴直径调节精度仅有1 mm),该方案在2种井底流压的情况下计算结果差别较大,但该方案的适应范围更宽,可以保证在22~24 MPa以最优的入流剖面进行生产,因此从对生产变化的适应性上来说,该方案可选为最优方案。
3 结论
(1)建立了适用于底水油藏ICD完井的油藏井筒耦合模型,能够更好地反映水平井生产入流形态。
(2)ICD优化设计与生产制度有很大关系,均匀入流剖面并非总可以当作目标入流剖面,应当根据实际储层情况和生产制度选择合适的目标入流剖面进行完井设计。
(3)非均匀ICD针对每一段选取最接近目标压降的ICD参数组合,调节精度较高,其最优结果一般优于均匀ICD完井方案。
(4)喷嘴型ICD压降对流速十分敏感,高生产压差可以有效发挥ICD的控流优势,对于定产量生产,建议使用高生产压差进行ICD完井设计。
(5)均匀ICD完井方案的适应性要优于非均匀ICD完井,不同生产压差情况下的最优均匀ICD方案可能相同,这使得均匀ICD完井放宽了对井底流压的要求,同时也简化了完井设计。
[1]LORENZ M D, RATTERMAN E E, AUGUSTINE J R. Uniform inflow completion system extends economic field life: a field case study and technology overview [R]. SPE 101895, 2006.
[2]HENRIKSENK H, GULE E I, AUGUSTINE J R.Case study: the application of inflow control devices in the Troll Field [R]. SPE 100308, 2006.
[3]KVERNSTUEN S, DOWLING K R, GRAHAM J S, et al. ICD screen technology in stag field to control sand and increase recovery by avoiding wormhole effect [R]. IPTC 12385, 2008.
[4]LI Fernandes Z, ZHU P X, Understanding the roles of inflow-control devices in optimizing horizontal-well performance [R]. SPE 124677, 2009.
[5]OUYANG L B. Practical consideration of an inflowcontrol device application for reducing water production[R]. SPE 124154, 2009.
[6]AL-KHELAIWI F T, DAVIES D R. Inflow control devices: application and value quantification of a developing technology [R]. SPE 108700, 2007.
[7]YOUNGS B, NEYLON K J, HOLMES J A. Recent advances in modeling well inflow control devices in reservoir simulation [R]. IPTC 13925, 2009.
[8]BIRCHENKO V M, et al. Application of inflow control devices to heterogeneous reservoirs [R]. Journal of Petroleum Science and Engineering, 2011(78): 534-541.
[9]AL-ENEZI K, DAS O P, ASLAM M, et al. Water coning model for horizontal wells in high mobility reservoir, West Kuwait [R]. SPE 130302, 2010.
[10] DANESHY Ali, GUO Boyun, KRASNOV Vitaly, et al. Inflow-Control-Device Design:Revisiting objectives and techniques [R]. SPE Production & Operations, 2012-02: 44-51.
[11]GAVIOLI P, GARCIG A, SERRANO J C. Design, analysis, and diagnostics for passive inflow control devices with openhole packer completions[R]. OTC 20348, 2010.
[12]刘想平,郭呈柱,蒋志祥,等. 油层中渗流与水平井筒内流动的耦合模型[J]. 石油学报,1999,20(3):90-94.
[13]程林松.高等渗流力学[M].北京:石油工业出版社,2011.
[14]汪志明.油气井流体力学与工程[M]. 北京:石油工业出版社,2008.
[15]LAURITZEN J E, MARTINIUSSEN I B. Single and multi-phase flow loop testing results for industry standard inflow control devices [R]. SPE 146347, 2011.
[16]李立峰,岳湘安,张立娟. 考虑井筒压降的底水油藏水平井见水时间研究[J]. 西安石油大学学报:自然科学版,2012,27(4):46-49.
[17] MARZOUQI A L, HELMY A A,KESHKA R H, et al. Wellbore segmentation using Inflow Control Devices: Design & Optimization Process [R]. SPE 137992, 2010.
[18] 冯福平,艾池,崔志华,等.水平井偏心环空顶替流体密度差优化[J].石油钻采工艺,2014,36(1):61-65.
(修改稿收到日期2015-06-12)
〔编辑薛改珍〕
Calculation method for ICD completion coupling model and target profile of horizontal wells in heterogeneous bottom water reservoir
FU Xuan1, LI Gensheng1, CUI Mingyue2, HUANG Zhongwei1, LIANG Yuesong1
(1. State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum, Beijing 102249, China; 2. Langfang Branch of Research Institute, Petroleum Exploration and Development, CNPC, Langfang 065007, China)
The Inflow Control Device (ICD) has been increasingly used in staged completion of horizontal wells in recent years. However, the semi-analytical coupling model built for ICD completion cannot accurately reflect the end effect in horizontal wells, and there is a lack of basis for the selection of target inflow profile during ICD optimization design. Therefore, a reservoir seepage model was first introduced based on potential superposition principle and specular reflection principle to accurately reflect the inflow features of horizontal wells, and a steady state coupling model was built which was suitable for ICD completion of heterogeneous bottom water reservoirs. Thereafter, in view of different production systems of oil wells, this paper provides the determination method for optimized target inflow profile of horizontal wells in heterogeneous reservoirs completed with ICD, describes in detail the design procedure of ICD taking nozzle-type ICD as an example and compares and analyzes the calculation results of optimal non-uniform ICD and optimal uniform ICD. The result shows that the optimized design of ICD is closely related to production system and uniform inflow profile is not always the ideal inflow profile. The flow control effect of non-uniform ICD is superior to that of uniform ICD, but well completion with uniform OCD is more widely adaptable to the bottom hole flow pressure. The high production pressure difference helps bring to play the flow control advantage of nozzle-type ICD.
heterogeneous; bottom water reservoir; ICD; coupling model; target profile
TE249
A
1000 – 7393( 2015 ) 04 – 0027– 06
10.13639/j.odpt.2015.04.008
中国石油天然气集团公司“十二五”海外重大科技攻关项目“中东地区大型碳酸盐岩油藏采油工程技术研究与应用”(编号:2011E-2502);国家自然科学基金创新研究群体项目“复杂油气井钻井与完井基础研究”(编号:51221003)。
付宣,1983年生。现主要从事水平井分段液流控制完井方向研究,在读博士生。电话:010-89733988。E-mail: fuxuan1998 @aliyun.com。通讯作者:李根生。电话:010-89733935。E-mail:ligs@cup.deu.cn。
引用格式:付宣,李根生,崔明月,等.非均质底水油藏水平井ICD完井耦合模型与目标剖面计算方法[J].石油钻采工艺,2015,37(4):27-32.
