倾角对倾斜光纤光栅光谱特性的影响
2015-09-24高宇飞牟海维张勇刘超
高宇飞 牟海维 张勇 刘超

摘要: 基于倾斜光纤光栅模式耦合理论,研究了倾斜角度对光纤光栅光谱特性的影响,并应用OptiGrating 软件进行数值模拟仿真。通过对不同倾斜角度得到的光纤光栅反射谱及透射谱的研究发现,随光栅倾角的增大,布拉格波长的中心波长偏移,同时反射率下降,而包层模式耦合增强,透射损耗变大,群时延减小。仿真结果对光纤光栅的设计和优化有一定的指导意义。
关键词: 倾斜光纤光栅; 倾斜角度; 光谱特性
中图分类号: TN253 文献标志码: A doi: 10.3969/j.issn.1005-5630.2015.04.012
Abstract: Based on the mode coupling theory, the effect of titled angle on the characteristics of spectrum of fiber grating is proposed. The numerical modeling method is performed by using the software, OptiGrating.By considering the reflection and the transmission spectra, we find that the central wavelength shifts to the long-wave band, the reflectivity of Bragg wavelength decreases, the cladding mode couplings are enhanced,the transmittance becomes larger,and the group delay decreases intensely with the increase of the titled angles. This conclusion provides a theoretical guidance for the design and optimization of fiber grating.
Keywords: titled fiber Bragg grating; titled angle; spectral characteristics
引 言
在光纤光栅的制作过程中,如果光栅平面倾斜了一定角度,就形成了一种新型光纤光栅即倾斜光纤光栅(tilted fiber Bragg grating,TFBG)。与光纤Bragg光栅相比,其前向传导的入射光除了一部分耦合为后向传导的纤芯模外,随着倾斜角度的增大,纤芯导模到包层模以及辐射模的耦合也会变强,从而产生区别于光纤Bragg光栅的光谱特性。虽然对TFBG的理论和实验研究起步较晚,但随着研究的深入,人们发现其具备光纤Bragg光栅和长周期光纤光栅的优点。在传感领域,除了温度、应变外,其对环境折射率极其敏感,可制成精度更高的折射率传感仪,使其在石油化工、环境监测等领域有着更广泛的应用前景[1-4]。对于TFBG,当倾斜角度、栅长、光栅周期、折射率调制等结构参数发生变化时,都会导致其光谱特性的改变。其中的倾斜角度无疑是最重要的结构参数,改变倾斜角度其反射谱及透射谱的形状、位置、深度等都将发生变化。本文将根据倾斜光纤光栅的结构特点,基于耦合模理论,仿真模拟倾斜角度对TFBG光谱特性的影响,从而为光纤光栅的制作及应用提供一定的理论指导。
1 倾斜光纤光栅的结构模型
倾斜光纤光栅属于均匀光纤光栅的一种,其折射率调制条纹不再像光纤Bragg光栅那样垂直于光纤的轴向,而是与光纤轴向存在一定的倾角θ,其结构如图1所示。
2.2 仿真结果与分析
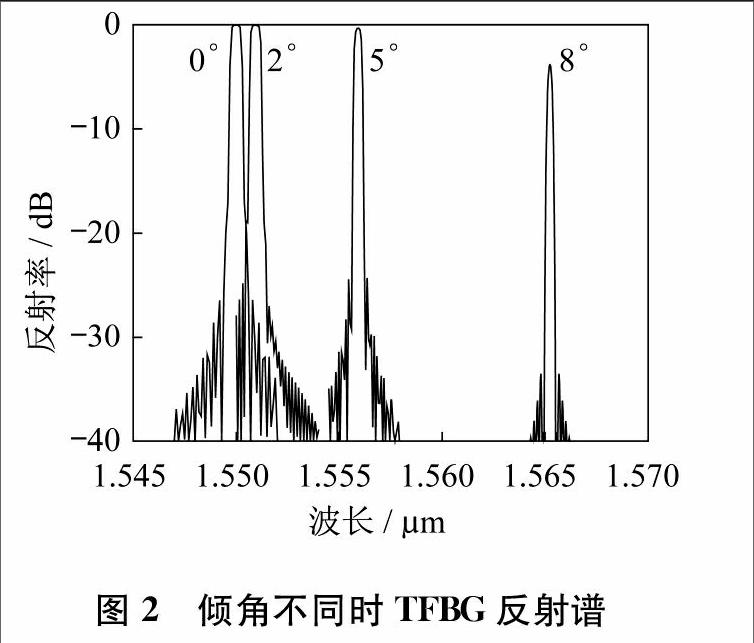
使用加拿大OPTIWAVE公司开发的光纤光栅分析软件OptiGrating对TFBG的反射谱进行数值模拟与仿真。这里通过改变光栅的倾角,模拟仿真光栅的反射谱。光栅参量为:纤芯半径为2 μm,折射率1.46,光栅周期为0.533 8 μm,光栅长度为10 mm,波长范围为1.545~1.570 μm,步长为1 000,折射率调制深度为0.001,中心波长为1.55 μm,模拟仿真出倾斜角度0°~30°时TFBG的反射谱,选取倾角为0°、2°、5°、8°的反射谱,如图2所示。
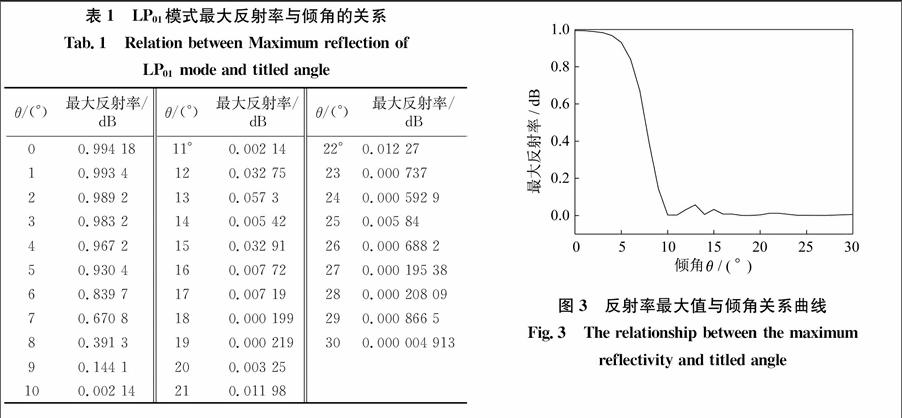
由图2可知,在倾斜角度较小时,耦合主要发生在正反向传输的纤芯基模LP01之间,在谐振波长处耦合最强,具有最大的反射率,纤芯导模与后向传输的包层之间耦合模式的透射率小,其光谱特性类似光纤Bragg光栅。随着角度增加,中心波长向长波段移动,该波长红移是由于光栅的倾斜导致其沿长度方向的栅格周期增加而引起的。当倾斜角度较大时,其峰值波长的反射率下降,同时反射带宽变窄。此现象表明,由于倾角的存在使得光栅模式的耦合发生了变化,光栅对反向传输的纤芯模的耦合能力减弱。计算得到倾角和LP01模式最大反射率的对应关系数据,如表1所示。基于表1的数据,图3 给出了布拉格中心波长(正反向传输的基模LP01耦合而成)最大反射率与倾斜角度的关系曲线。
在图3中,横坐标为倾斜角度,纵坐标为对应的中心波长最大反射率,反映了不同倾角的光纤光栅对反向传输纤芯模式的耦合能力。从图中可以看出,中心波长的最大反射率随着角度增加迅速下降,在倾斜角度较小时(θ≤5°)时,耦合效率下降幅度较小,纤芯基模的反射率变化不明显,随着倾斜角度的增大(10°≥θ≥5°),光栅的反射率迅速下降,比如倾斜角度7°到8°,反射率下降达到了30%,倾角角度为10°时,TFBG的反射率几乎为零,此时的光栅只有透射峰。此后随着角度的变化,反射率有小幅度的波动,出现了局部的最大值和最小值。而从式(6)可知,当交流耦合系数κ=0时,对应的反射率会出现最小值,在一些特殊的应用场合如反射不被允许的条件下可以将光栅的倾斜角度设置在该点。
结合传输矩阵法,并应用OptiGrating软件仿真,采用前述的光栅参数,增加其包层参数如下:包层半径60.5 μm,包层折射率1.45,分析不同倾斜角度对TFBG包层模传输特性的影响,由于包层模式间的耦合很弱,所以只考虑纤芯LP01与一阶包层模LP1μ耦合的情况,耦合模数为100,图4得到TFBG的透射光谱如图4所示。
由光谱图上可以看出,倾角的逐渐增加,TFBG的透射谱中出现了较多的包层模谐振峰。图4(a)当θ=0°时,布拉格谐振峰位于中心波长1.55 μm处,是由于正反向基模LP01之间的耦合而成,由于其反射率最大,则透射峰深度最大,同时短波区出现了一系列的分立的包层模谐振峰,此时倾斜光栅为Bragg反射光栅。图4(b)当模板倾斜角度θ=3°时,随着包层模耦合的增强,短波区出现更多的包层模式耦合,即为正向传输的纤芯模式LP01与反向传输的一阶包层模式的耦合而成的透射峰,纤芯模的损耗峰变小。图4(c)当倾斜角度为10°时,主模LP01模式的耦合系数接近为零,此时光栅Bragg 反射接近为零,此时的光栅只有透射峰,右侧主模LP01的透射峰较包层模要小,其透射深度为-0.092 dB,此时的透射率达到了98%,其左侧的一系列包层模式谐振峰深度增加,其中纤芯导模LP01与1阶63次包层模LP1,63耦合的透射深度最大为-1.2 dB,换算成透射率为76%,包层模式的透射峰带宽大大增加;如果倾角继续增大,耦合模式就变成了纤芯前向导模与包层前向导模透射率之间的耦合,倾斜光栅为透射型光栅,如图4(d)。
4 TFBG的群时延特性
通过研究发现,通过调制光纤光栅的某些物理参数获得特定的群时延从而将其应用做延迟器件,因此群时延特性也是光纤光栅光谱特性的一个重要指标[9]。光纤光栅的反射光的群时延可表示为
τ=dψRdω=-λ22πcdψRdλ(10)
式中ψR为相位。
根据Bragg光纤光栅的原理,在谐振波长附近群时延出现最小值即接近于零,说明光纤Bragg光栅对满足其谐振条件的光有很强的耦合作用,当靠近反射带边缘时,由于光耦合率较小,因而具有相对较大的群时延。为了研究TFBG倾角与群时延曲线的关系,所选参数如下:纤芯半径2 μm,纤芯折射率1.46,光栅长度5 mm,周期0.534 μm,折射率调制深度0.001,谐振波长1.55 μm,保持所设参数不变的情况下,分别取TFBG的倾角为0°、3°、5°、8°得到均匀TFBG群时延τ与波长λ的变化曲线,如图5所示。
可以看出,随着倾斜角度θ的增加,TFBG对应的群时延与反射谱曲线一样,向长波长方向移动,当角度从0°增加到8°时,中心波长从1.55 μm移动到1.563 μm,同时随着倾角的增加,对应的群时延急剧减小,群时延最大值从32.73 ps下降到25.14 ps。
5 结 论
倾斜光纤光栅由于其特殊的结构特点,正被广泛地应用于诸多传感领域,尤其在测量应变、折射率等方面具有更加广阔的市场前景。本文对倾斜光纤光栅的光谱特性进行了理论和仿真研究,考察了倾斜角度对TFBG的Bragg散射和包层模耦合的光谱特性影响,并得到了不同倾角对应的最大反射率的数值结果,验证了倾斜角度对群时延特性的影响。
参考文献:
[1] XU O,LU S H,JIAN S S.Theoretical analysis of polarization properties for titled fiber Bragg gratings [J].Science China Information Siences,2010,53(2):390-397.
[2] 郑崇伟,戴瑜兴.倾斜对光纤光栅反射特性的影响[J].光电子技术,2006,25(1):25-27.
[3] 欧启标,苏百顺,曾庆科,等.倾斜光纤光栅谱特性[J].光子学报,2012,41(4):414-420.
[4] 刘超,孙祺,柴雅婷,等.倾斜光纤光栅周期对其透射谱的影响[J].光学仪器,2014,36(1):58-61.
[5] CHEN X F,ZHOU K M,ZHANG L,et al.Optical chemsensor based on etched titled Bragg grating structures in multimode fiber[J].IEEE Photonics Technology Letters,2005,17(4):864-866.
[6] HILL K O,MELTZ G.Fiber Bragg grating technology fundamentals and overview[J].Journal of Lightwave Technology,1997,15(18):1263-1276.
[7] ERDOGAN T.Fiber grating spectra[J].Journal of Lightwave Technology,1997,15(8):1277-1294.
[8] CAO CHETEOR C ,SHEVCHENKO Y,SHAO L Y,et al.High resolution interrogation of tilted fiber grating SPR sensors from polarization properties measurement[J].Optics Express,2011,19(2):1656-1664.
[9] 饶云江,王义平,朱涛.光纤光栅原理与应用[M].北京:科学出版社,2006.
(编辑:张磊)
