双馈风机附加阻尼控制环节与PSS的参数协调优化
2015-09-24郑华,李忠,陈凡
郑 华,李 忠,陈 凡
(1.国电南京自动化股份有限公司,江苏南京210032;2.南京灿能电气自动化有限公司,江苏南京211100;3.安徽省电力科学研究院,安徽合肥230601)
双馈风机附加阻尼控制环节与PSS的参数协调优化
郑华1,李忠2,陈凡3
(1.国电南京自动化股份有限公司,江苏南京210032;2.南京灿能电气自动化有限公司,江苏南京211100;3.安徽省电力科学研究院,安徽合肥230601)
对于含双馈风电场的多机电力系统,在双馈风机内部引入附加阻尼控制环节可以抑制系统低频振荡,但双馈风机附加阻尼控制环节可能会影响电力系统稳定器(PSS)抑制低频振荡的效果。提出了一种双馈风机附加阻尼控制环节与PSS的参数协调优化方法,设计了兼顾机电振荡模式和非机电振荡模式的阻尼特性的优化目标函数,并给出了基于粒子群算法的求解方法。以三机系统作为算例,优化设计了双馈风机附加阻尼控制环节与PSS的参数。时域仿真结果表明,所提出的参数协调优化方法可以更好地提升系统的阻尼,有利于低频振荡的快速平抑。
双馈风机;低频振荡;附加阻尼控制;PSS;协调优化;粒子群算法
随着风电场发电容量在电网中所占的比例不断提升,其对电力系统的小干扰稳定性和阻尼特性将带来一定影响[1,2]。研究表明,对于含大容量双馈型风电场的多机电力系统,在双馈风机内部配置相关控制器可改善系统的阻尼[2-4]。目前,抑制低频振荡的主要手段有电力系统稳定器(PSS)、灵活交流输电系统(FACTS)、直流调制等[5,6]。各个手段之间可能存在负影响,因此研究各手段之间的协调控制具有工程意义。文献[7]提出一种基于Prony算法的PSS和直流附加控制器协调运行的策略。文献[8]提出将加入混沌优化算法和模拟退火思想的改进粒子群算法用于协调优化飞轮储能稳定器与PSS参数。文献[9]对多机系统中PSS和FACTS的参数协调优化进行了研究。目前,双馈风机附加阻尼控制环节与PSS的参数协调优化尚属较新的课题,随着风电并网容量的增加,该问题具有较大的研究价值。
文中对双馈风机附加阻尼控制环节与PSS之间的参数协调优化作了探索性研究,提出了基于粒子群算法的参数协调优化方法,在目标函数中兼顾了机电振荡模式和非机电振荡模式的阻尼特性。以三机系统作为算例,对比了参数协调优化方法与参数独立设计方法的阻尼改善效果,验证了参数协调优化方法的有效性。
1 双馈风机附加阻尼控制环节的作用原理
PSS的主要原理是通过输入频率、电磁功率等偏差信号,输出相应的附加控制信号控制励磁进而对发电机转子振荡提供阻尼作用。与同步发电机不同,双馈风机主要通过变频器控制其注入系统的电磁功率。双馈风机附加阻尼控制环节通过控制变频器输出与系统振荡相关的阻尼功率,进而产生一个附加阻尼转矩,起到改善系统阻尼的作用[2]。
双馈风机转子侧变换器采用定子磁链定向的矢量控制策略,控制框图如图1所示[10]。图中:Kp1和Ki1为转子侧变换器有功控制环节的PI控制参数;Kp2和Ki2为转子侧变换器电流控制环节的PI控制参数;Kp3和Ki3分别为转子侧变换器无功控制环节的 PI控制参数;idr_ref和 iqr_ref为转子电流 d轴和 q轴参考值;Pref和Qref为无功功率和有功功率参考值;Ps和Qs分别为定子有功和无功功率的测量值;x1,x2,x3,x4为引入的4个中间状态变量。文中在双馈风机转子侧变换器的有功控制回路中引入附加阻尼控制环节,该环节以双馈电机转差率偏差Δs作为输入信号,输出一个附加输出信号vs作用到转子电压q轴分量vqr上。
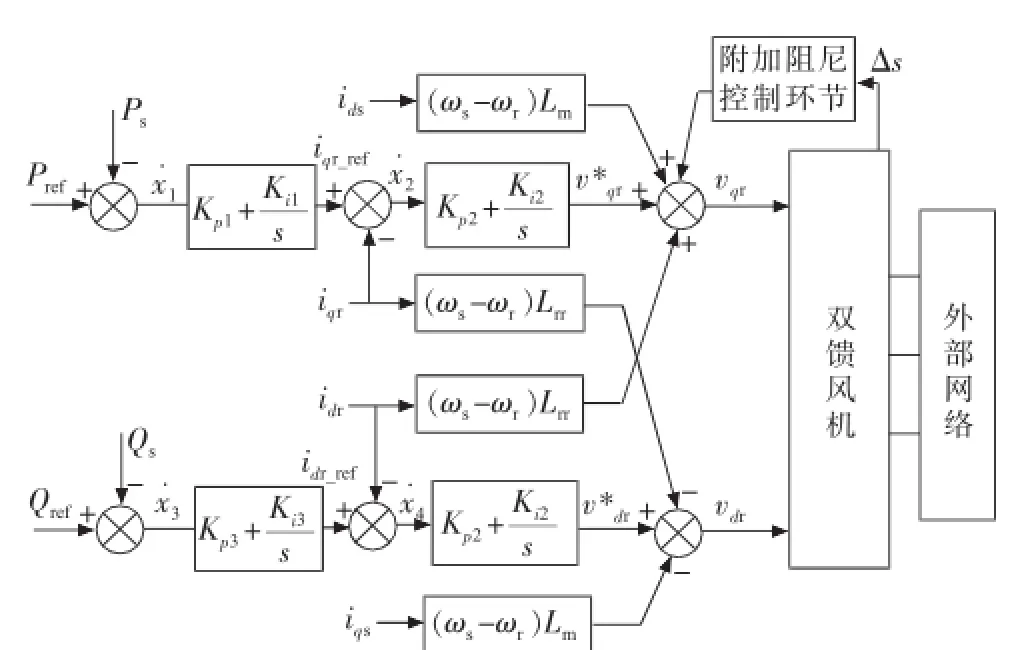
图1 转子侧变换器控制框图
附加阻尼控制环节的内部结构如图2所示,主要是由增益单元、隔直单元、超前滞后单元和限幅单元等组成。
图中:K为增益;Tw为隔直环节时间常数;T1~T4分别为两级超前滞后环节时间常数。转子侧变换器采用定子磁链定向的矢量控制策略,忽略定子磁链暂态过程和定子电阻,可以得到电磁转矩表达式[2,11]:
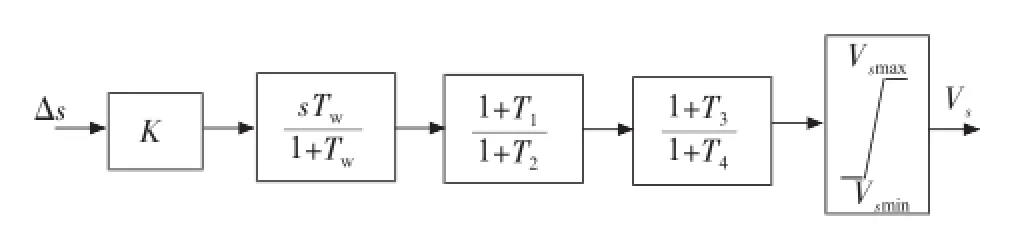
图2 附加阻尼控制环节结构
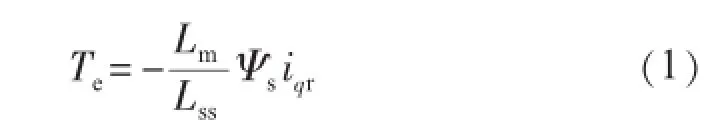
式中:Te为风机电磁转矩;Lss,Lm分别为dq坐标系下等效的定子自感、定转子互感;Ψs为定子磁链。忽略定子磁链暂态,可认为定子磁链恒定不变。因此,双馈风机的电磁转矩可由转子电流轴q分量iqr独立控制。
转子电流和转子电压存在如下的控制关系[2]:
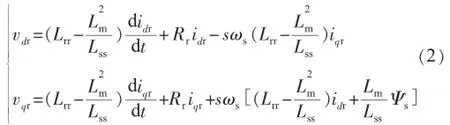
由上式可知,转子电流的d,q轴分量可以由转子电压d,q轴分量分别控制,但上述两式的第三项为交叉耦合项,这些耦合干扰了转子电压对转子电流的控制作用,可看成系统的内扰动。由控制理论可知,闭环控制具有消除环内扰动的性能,因此如图1所示,通过双闭环PI控制可以较好实现vdr,vqr各自对idr,iqr的控制作用。
合理整定附加阻尼控制环节的参数,当系统发生振荡时,可以使得该环节的输出信号vs作用到转子电压q轴分量vqr上,进而调整转子电流q轴分量iqr的大小,产生一个与Δω同相的附加电磁转矩ΔTe,即可以起到增强系统阻尼的作用。
2 基于粒子群算法的参数协调优化
2.1系统模型
双馈风机附加阻尼控制环节或PSS的传递函数可以表示成以下统一形式:
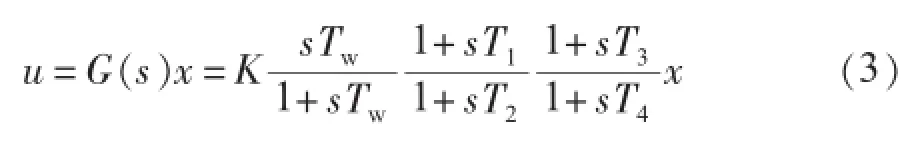
双馈风机附加阻尼控制环节的输入信号x取转差率偏差Δs,PSS的输入信号取转速偏差Δω。
双馈风机建模方面,采用平均风速模型,风力机机械传动部分采用单质量块模型,双馈感应电机采用3阶简化模型,忽略网侧变换器的动态作用,只对转子侧变换器及其控制系统进行动态建模。双馈风机的线性化模型可用如下方程组表示:

式中:TJ为单质量块模型的等效惯性时间常数;s为风机转差率;E'd和E'q分别为dq轴暂态电压;Lrr为dq坐标系下等效的转子自感;ωB为转速标幺值。
考虑包含同步发电机和双馈风机这两种动态元件的多机系统,消去负荷节点后全系统的网络方程线性化形式可写成:

式中:ΔVg,ΔVw,ΔVl分别为同步发电机节点、风机节点和其他联络节点的电压偏差;ΔIg,ΔIw分别为发电机节点和风机节点的注入电流偏差;以不同下标表示发电机、风机和输电线路之间的导纳分块矩阵。由该方程可获得含双馈风机的多机系统状态矩阵A,并可以计算出全系统的特征根和特征向量,利用特征值分析法研究系统的小干扰稳定性和低频振荡特性。
2.2优化目标函数
协调优化过程中兼顾机电振荡模式和非机电振荡模式,在增强系统小干扰性能的同时,避免对系统的其他动态性能产生负面影响。在参数优化过程中选取几种典型运行方式作为主要运行方式,增强优化结果的鲁棒性。因此,文中兼顾机电振荡模式和非机电振荡模式特性的目标函数如下:
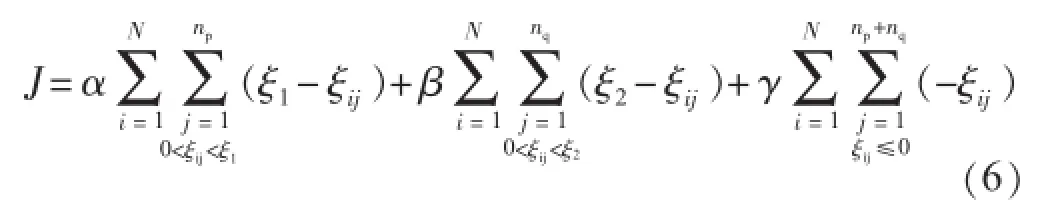
式中:N为典型运行方式的数目;np为机电振荡模式的个数;nq为非机电振荡模式的个数;ξ1和ξij分别是机电振荡模式和非机电振荡模式阻尼比的门槛值,ξ1为第i种运行方式下第j个振荡模式的阻尼比;α和β分别为相应的权重系数;γ是对负阻尼振荡模式的惩罚因子,一般取值较大,用以加重对负阻尼振荡模式的惩罚,以便更快速地寻到最优解。因此,附加阻尼控制环节与PSS参数的协调优化问题可描述为:
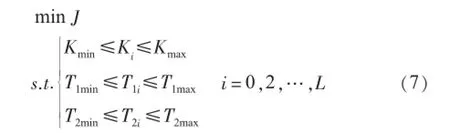
式中:L为多机系统中需要配置的附加阻尼控制环节和PSS的个数;Kmin,Kmax为增益环节的最小值和最大值;T1max,T2max为时间常数最大值;T1min,T2min为时间常数最小值。一般可假定两级超前滞后环节相同,即有T1i=T3i,T2i=T4i,因此只需对每个附加阻尼控制环节和PSS的Ki,T1i,T2i进行优化即可。
2.3粒子群算法及优化流程
粒子群算法[12]是受到人工生命研究结果的启发而提出的。令整个粒子群经过的最优位置为Pq,即全局最优(gbest)。每个粒子的位置变化按公式(6)、(7)进行:
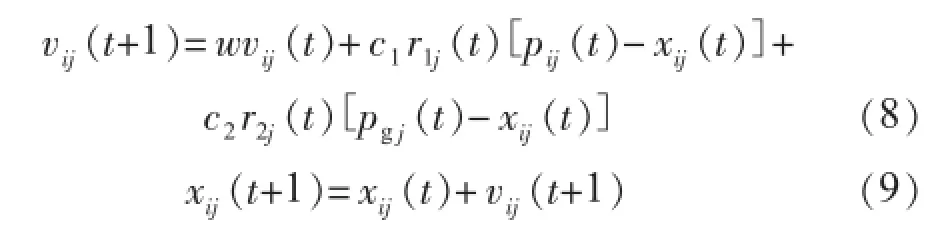
式中:下标j代表粒子的第j维;i代表第i个粒子;t代表第t代;w为惯性因子;c1,c2为加速因子,取值一般在0~2之间;r1~U(0,1),r2~U(0,1)为2个相互独立的随机函数。
粒子群算法具有数学逻辑简单、无需采用二进制编码、目标函数实现容易以及对优化目标灵敏性较高等优点,是解决全局优化问题的常用手段。
在Matlab中编制程序,采用粒子群算法实现参数协调优化,主要步骤如下:(1)利用特征值分析程序获取系统的状态矩阵,并初始化粒子群的速度和位置;(2)更新状态矩阵中Ki,T1i,T2i的值,求解状态矩阵的特征值及对应的阻尼比;(3)计算目标函数值,并将其作为当前适应度,更新pbest和gbest,进而更新每个粒子的Vi和Xi;(4)判断是否满足终止条件,若满足则退出,否则跳至步骤(2)。
基于粒子群算法的附加阻尼控制环节与PSS参数协调优化流程图如图3所示。
3 算例分析
以三机系统作为算例,验证参数协调优化方法的有效性。系统拓扑结构如图4所示,该系统是以IEEE三机9节点系统作为基本框架,又在其中接入了大容量双馈型风电场,并参照文献[13]中的算例数据对发电机和负荷的有功、无功进行了调整。系统基准容量为100 MV·A,基准电压为230 kV,频率为60 Hz。
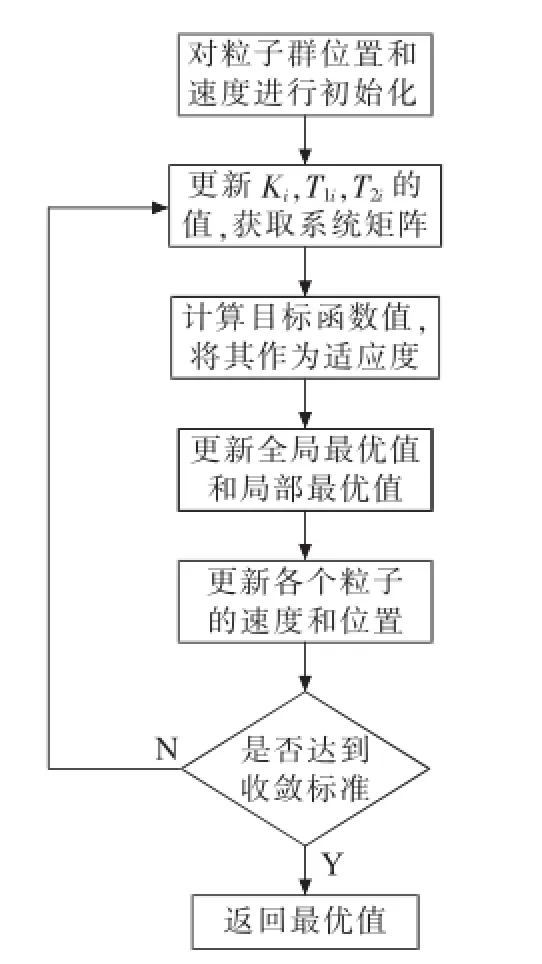
图3 基于粒子群算法的参数协调优化流程
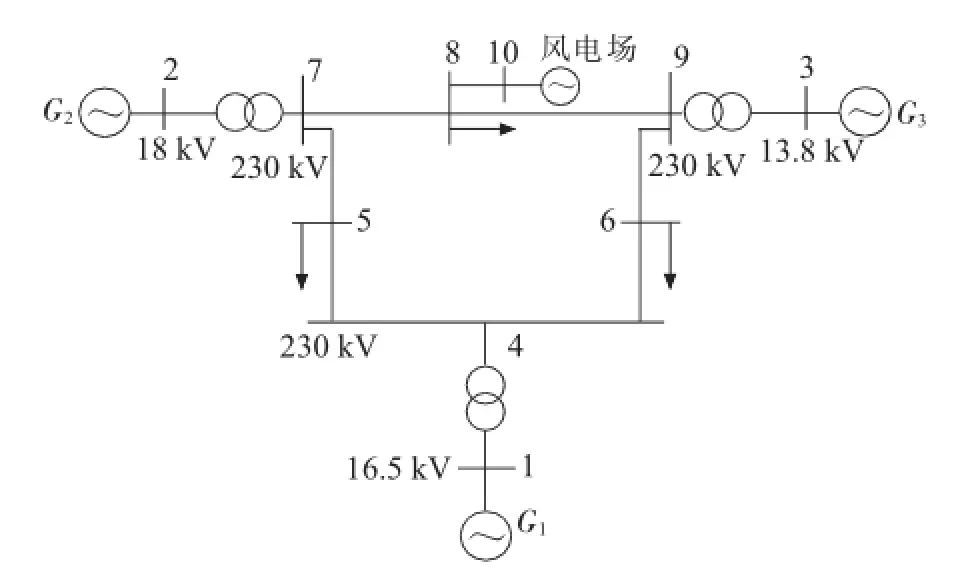
图4 3机系统拓扑结构
双馈型风电场在10号节点处接入系统,风电场容量为90 MW,双馈风机采用恒功率因数 (取cosφ= 0.95)控制方式运行,并采用1台等值机对风电场进行等效。节点1、2、3分别接入同步发电机,3台机励磁系统均采用一阶惯性环节模拟。节点5、6、8为负荷节点,采用恒阻抗模型等效。
双馈风机的运行状态一般分为超同步 (s<0)、同步(s=0)和次同步(s>0)3种,取风机运行在s=-0.2,s=0.1和作为系统的3种典型运行方式。
3.1特征值分析
在Matlab中编制特征值分析程序,得到系统在3种典型运行方式下的特征值情况如表1所示。由表1可看到,三机系统含有3个机电振荡模式,振荡频率为1.8 Hz的模式阻尼为负,属于失稳模态。
为了对比参数协调优化法与参数独立设计法的阻尼改善效果,在2号发电机G2、3号发电机G3上配置PSS,在双馈风机上配置附加阻尼控制环节,分别采用上述2种方法设计附加阻尼控制环节和PSS参数。
先采用参数协调优化方法设计附加阻尼控制环节和PSS的参数。该算例中可设定增益的取值范围为[0.1,150],T1i,T2i的取值范围为[0.01,1]。利用粒子群优化算法对参数进行协调优化,得到优化后的参数如表2所示,目标函数的收敛曲线如图5所示。
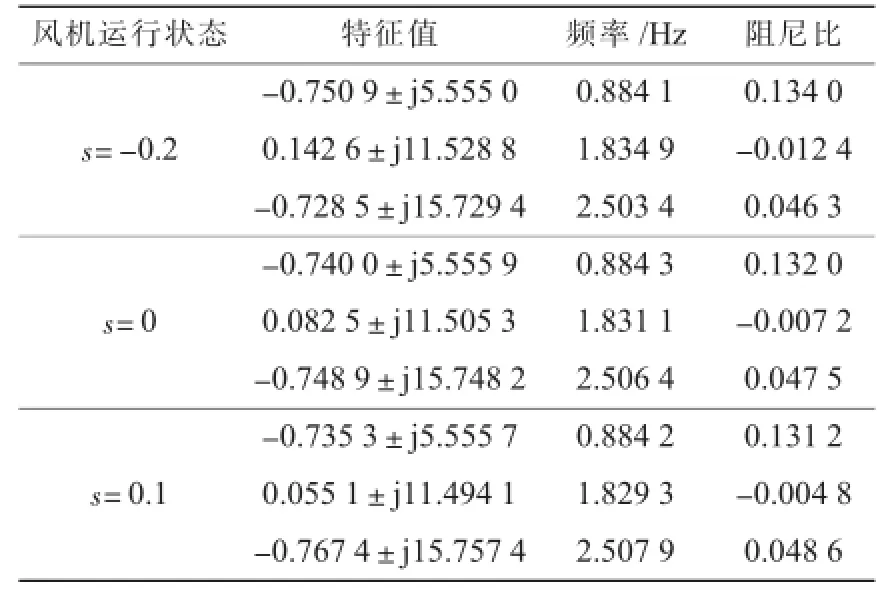
表1 三机系统机电振荡模式
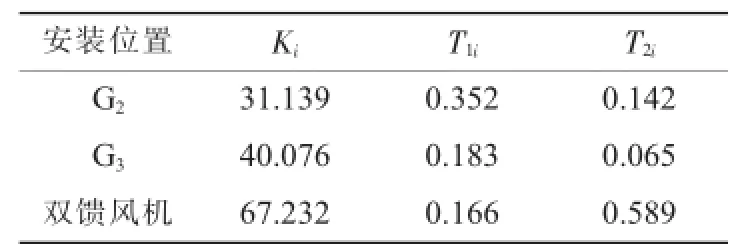
表2 协调优化后的参数
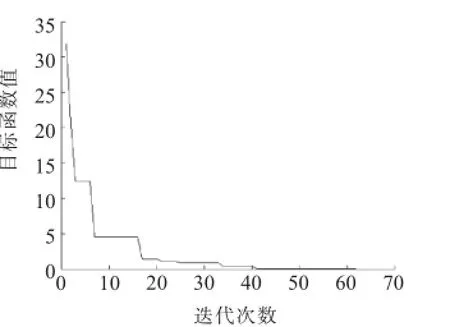
图5 最佳适应度和平均适应度随迭代次数的变化
附加阻尼控制环节与PSS的参数经过协调优化后,系统的机电振荡模式如表3所示。
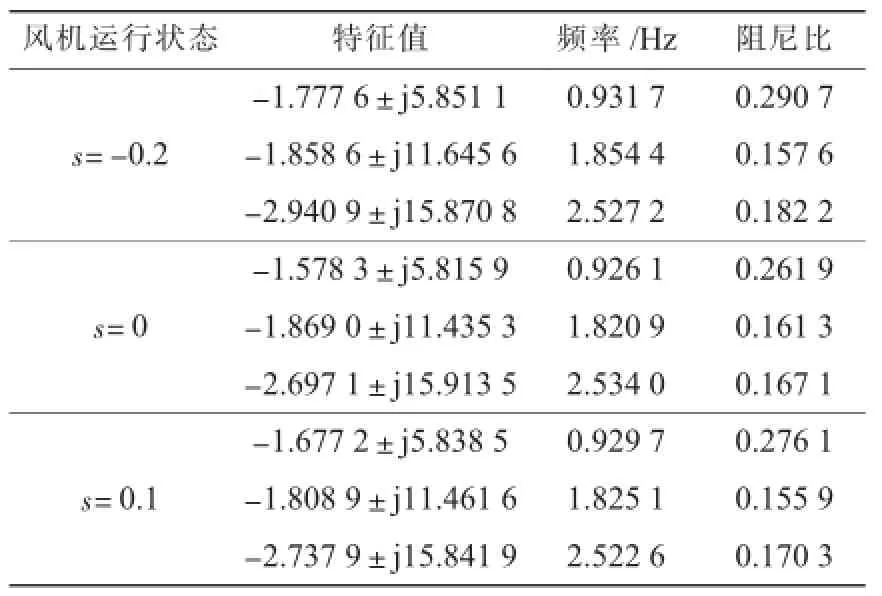
表3 参数协调优化后系统的机电振荡模式
再采用参数独立设计方法设计附加阻尼控制环节和PSS的参数,独立设计参数时采用相位补偿法,其参数如表4所示,参数独立设计后系统的机电振荡模式如表5所示。
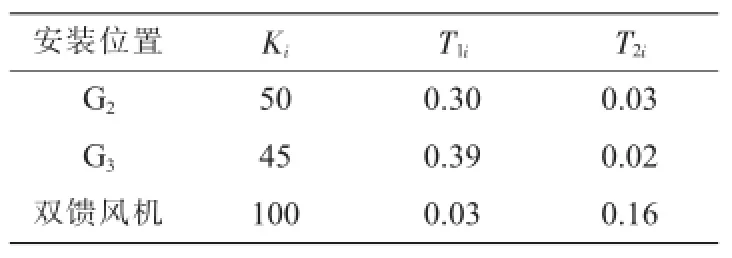
表4 独立设计后的参数
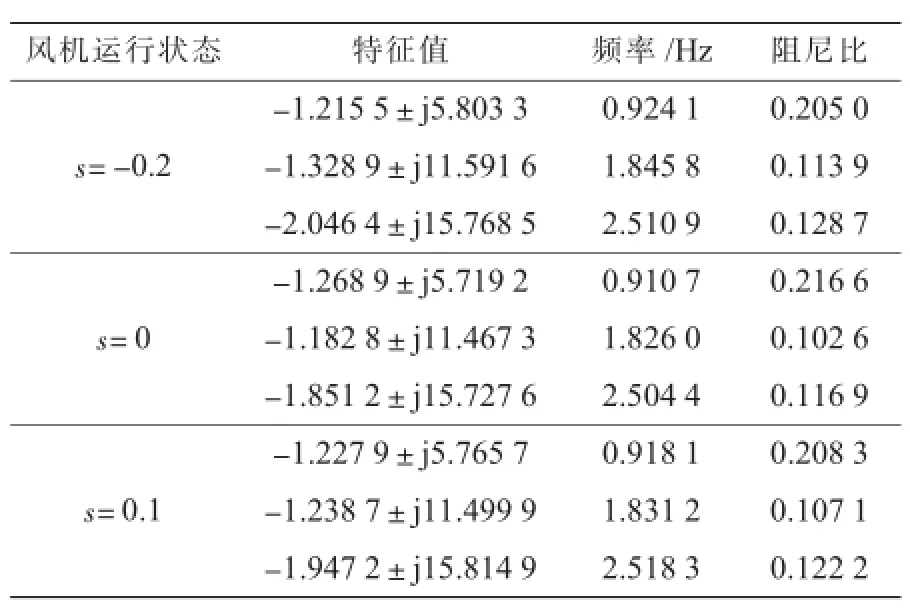
表5 参数独立设计后系统的机电振荡模式
对比表3和表5的模态分析结果可以看到,2种方法都能有效改善系统阻尼,但参数协调优化方法相比参数独立设计方法,在保证所有振荡模式均不失稳的情况下,能使系统阻尼从非机电振荡模式向机电振荡模式发生合理转移,全面改善系统的阻尼,更有助于提升系统的运行稳定性。
3.2时域仿真
以风机工作在s=-0.2运行方式为例,设置节点7和8之间的线路在t=0.2 s时发生三相短路故障,故障持续0.1 s后自动消除并恢复正常运行,时域仿真结果如图6所示(选取1号发电机作为参考机)。
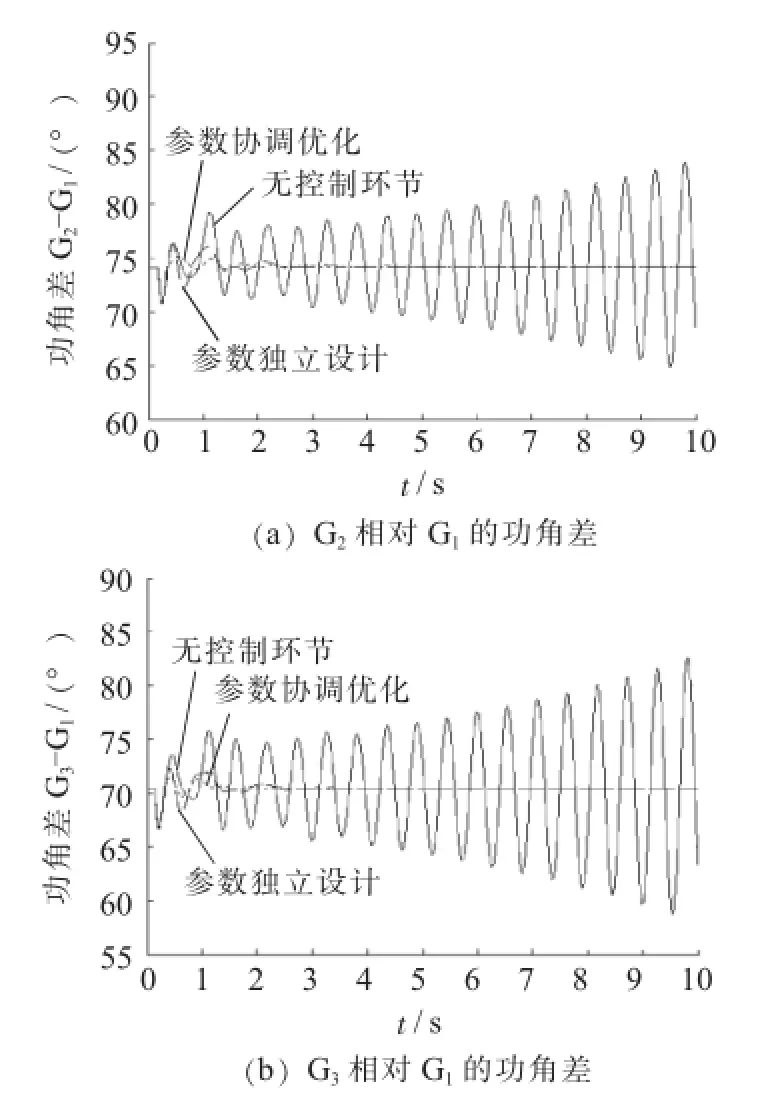
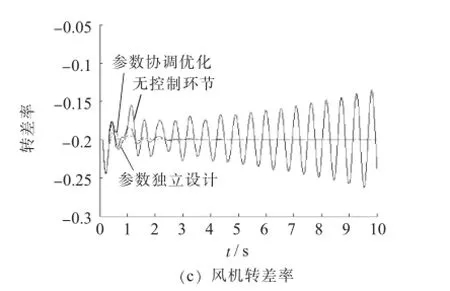
图6 故障后系统的功角差曲线和转差率曲线
由上述时域仿真结果可以看到,双馈风机附加阻尼控制环节和PSS的参数经过协调优化设计后,系统具有更好的阻尼特性,能够更加有效、快速地平抑低频振荡。时域仿真结果与特征值分析结果相吻合,从而证明了参数协调优化设计的优越性。
4 结束语
对双馈风机附加阻尼控制环节与PSS的参数协调优化问题进行了初步研究,提出了基于粒子群算法的参数协调优化方法,在目标函数中兼顾了机电振荡模式和非机电振荡模式的阻尼特性。以三机系统作为算例,从特征值分析和时域仿真两方面验证了上述方法的有效性。结果表明,所提出的参数协调优化方法可以更好地改善系统的阻尼,有利于系统的稳定运行。
[1]SLOOTWEG J G,KLING W L.The Impact of Large Scale Wind Power Generation on Power System Oscillations[J].Electric Power System Research,2003,67(1):9-20.
[2]关宏亮.大规模风电场接入电力系统的小干扰稳定性研究[D].北京:华北电力大学,2008.
[3]MICHEAL HUGHES F,ANAYA-LARA O,JENKINS N,et al.A Power System Stabilizer for DFIG-based Wind Generation[J]. IEEE Transactions on Power Systems,2006,21(2):763-772.
[4]郝正航,余贻鑫,曾 沅.改善电力系统阻尼特性的双馈风电机组控制策略[J].电力系统自动化,2011,35(15):26-29.
[5]王 康,金宇清,甘德强,等.电力系统小信号稳定分析与控制综述[J].电力自动化设备,2009,29(5):10-19.
[6]毛晓明,管 霖,张 尧,等.超高压大功率直流输电系统的先进控制技术应用及发展[J].电力自动化设备,2004,24(9):91-95.
[7]魏 巍,王渝红,李兴源,等.交直流电力系统PSS和直流附加控制的协调[J].电力自动化设备,2010,30(1):53-61.
[8]史林军,张 磊,陈少哺,等.多机系统中飞轮储能系统稳定器与PSS的协调优化[J].中国电机工程学报,2011,31(28):1-8.
[9]ABIDO M A.Pole Placement Technique for PSS and TCSC-based Stabilizer Design Using Simulated Annealing[J].Electrical Power and Energy Systems,2000(22):543-554.
[10]WU F,ZHANG X P,GODFREY K,et al Small Signal Stability Analysis and Optimal Control of a Wind Turbine with Doubly Fed Induction Generator[J].IET Gener.Transm.Distrib,2007,1(5):751-760.
[11]赵仁德.变速恒频双馈风力发电机交流励磁电源研究[D].杭州:浙江大学,2005.
[12]KENNMEDY J,EBERHART R.C.Particle Swarm Optimization[C]//IEEE International Conference on Neural Networks,IV Piscataway NJ IEEE:Service Center,1995:1942-1948.
[13]杨黎晖,马西奎.双馈风电机组对电力系统低频振荡特性的影响[J].中国电机工程学报,2011,31(10):19-25.
Study on Parameter Coordination and Optimization of DFIG Auxiliary Damping Controlling Unit and PSS
ZHENG Hua1,LI Zhong2,CHEN Fan3
(1.Guodian Nanjing Automation Co.Ltd.,Nanjing 210032,China;2.Nanjing Canneng Electrical Automation Co.Ltd.,Nanjing 211100,China;3.Anhui Electric Power Research Institute,Hefei 230601,China)
Deploying auxiliary damping controlling unit in douly-fed induction generator(DFIG)is an effective way to suppress the low frequency oscillations in the multi-machine system with large-scale wind farms.However,auxiliary damping controlling unit in DFIG may reduce the positive damping provided by PSS.In this paper,a parameter coordination and optimization method for auxiliary damping controlling unit and PSS is proposed.Both electromechanical and non-electromechanical modes are considered in the objective function,and a calculation method based on the PSO is proposed.The three-machine system is taken for performance analysis,and the parameter of auxiliary damping controlling unit and PSS is designed.Time-domain simulation results show that the method can improve the performance of damping low frequency oscillation.
douly-fed induction generator;low frequency oscillation,auxiliary damping control;power system stabilizer;coordination and optimization;particle swarm optimization
TM712
A
1009-0665(2015)03-0025-05
2014-12-28;
2015-02-11
“十二五”国家科技支撑计划项目(2011BAA01B02)
郑华(1970),男,江苏南通人,工程师,从事电力系统自动化设备研究和应用工作;
李忠(1973),男,江苏启东人,高级工程师,从事电力系统自动化设备的研究和应用工作;
陈凡(1988),男,安徽铜陵人,硕士,从事电力系统运行控制工作。
