三分仓回转式空预器的详细热力计算方法

陈　欢，周克毅，黄军林

（东南大学能源与环境学院，江苏南京210096）

三分仓回转式空预器的详细热力计算方法

陈欢，周克毅，黄军林

（东南大学能源与环境学院，江苏南京210096）

为提高锅炉三分仓空预器的热力计算精度，根据三分仓空气预热器的传热机理及温度分布特点，结合各分仓之间的漏风，建立三分仓微元体数学模型，得到各分仓的微分解析式，采用迭代计算的方法得到各分仓流体平均温度及金属蓄热板的平均温度。某1000 MW三分仓回转式空预器算例表明，该算法具有较高的计算精度，能够考虑各分仓的漏风影响，且可划分数量不等的计算区域进行计算以满足不同的工程需求，可以得到金属蓄热板的平均温度分布，为低温腐蚀和积灰提供温度参考。

三分仓；微元模型；传热；对流；漏风

三分仓回转式空气预热器是一种旋转换热的装置，广泛应用于大型锅炉。锅炉的三分仓空气预热器与普通的二分仓回转式空气预热器相比，多出一个通道，它将空气流通区域分成一次风和二次风两个通道，满足不同空气出口压力和温度的要求。

三分仓空气预热器温度分布的精度对火电节能及换热元件腐蚀具有重要意义。目前，二分仓空气预热器的热力计算方法相对比较成熟［1］，而三分仓空气预热器的热力计算到目前为止并没有完整成熟的方法。文献［2］基于二分仓空气预热器热力计算推广到三分仓空气预热器热力计算。文献［3］利用数值方法研究了由偏微分方程得到的二维传热方程。文献［4］建立复杂的微分方程利用数值方法对内部的温度场进行了模拟。文献［5］考虑金属蓄热板竖直切面平均温度沿旋转方向的非线性特性得到出口空气温度的解析表达式。文献［6］以大量的试验和统计数据为基础，通过计算直接得到烟气－空气传热系数的变化量简化计算。文献［7］基于文献［5］中的方法推广到了四分仓的计算。上述文献介绍的方法存在一些不足，文献［2，3］没有考虑到蓄热板平均温度沿旋转方向的非线性特性；文献［4，5］计算量大，不适用于工程应用；文献［5，7］虽然避免了上述不足，但是均需将一、二次风合并处理，无法分别计算三分仓的一、二次风区的漏风。

文中在前期研究的基础上［5］，考虑三个仓之间的漏风差异，建立了三分仓微元体模型，同时考虑金属蓄热板竖直切面平均温度沿旋转方向的非线性及流体温度的非线性特性，对三分仓各个仓进行计算，无需将一、二次风合并处理，从而得到了三分仓空气预热器的详细热力计算方法，且可划分数量不等的计算区域进行计算，以满足不同的工程设计和分析需求。

1　数学模型

如图1所示，三分仓回转式空气预热器转子转动时，金属受热面依次经过烟气、二次风、一次风，高温烟气对金属受热面加热，金属再加热冷空气。可以利用微元体建立微元方程，然后在适当简化的条件下得到三分仓空气预热器的计算模型。

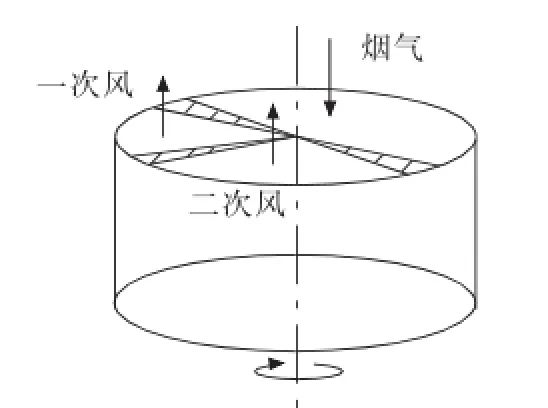
图1　三分仓回转式空气预热器传热示意图

1.1微元方程

根据空气预热器的工作原理、稳态工况下的流体以及受热面的能量平衡与传热关系可以建立空气预热器转子的微元方程。如图2所示，微元体的半径与空气预热器转子半径相同，角度为dβ。

图2　三分仓空预器微元体示意图

在忽略金属和流体轴向及切向导热的条件下，流体放热或吸热的微元体方程表示为：

受热面蓄热或放热的微元体方程表示为：

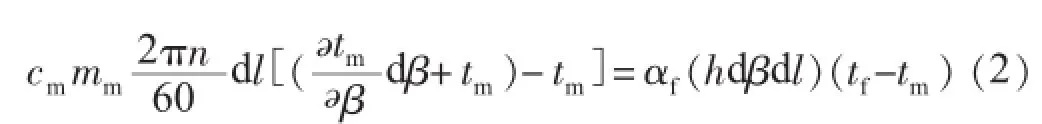
式中：cf为流体比热容，kJ/（kg·℃）；pf为流体密度kJ/m；wf为流速，m/s；a为单位弧度流体通流截面积，m2/rad；β为通道所占角度，rad；tf为流体温度，℃；l为受热面高度，m；αf为流体与金属的换热系数，kW/（m2·℃）；h为单位高度、单位弧度受热面的换热面积，m2/（rad·m）；tm为金属受热面温度，℃；cm为金属比热容，kJ/（kg·℃）；mm为单位高度、单位弧度金属质量，kg/（m·rad）；n为转子转速，r/min。由式（1）和式（2）可得到如下的微分方程：

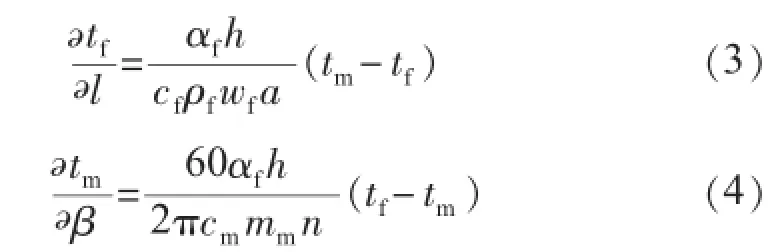
1.2计算区划分及漏风

式（3）、（4）的准确性与换热系数、流体的物性参数、金属的物性参数有密切的关系，均与温度相关，即与三分仓空预器内部温度场有关。理论上当空预器沿高度方向被分成的段数越多、沿圆周方向被分成的区域越多时，由式（3）和式（4）获得的温度场也更精确。但是，随分成区段增加，其计算量也会增加。考虑到空气预热器一般都分为热段、冷段，两者材料和板型均不同，为求解的简便，这里可将空预器分成冷热2段。整个空气预热器被分成6个区分别进行计算，即热段烟气区、热段二次风区、热段一次风区、冷段烟气区、冷段二次风区以及冷段一次风区。

在实际运行中，由于密封问题将不可避免造成各个区之间的漏风，包括一次风区向二次风区漏风、一次风区向烟气区的漏风，以及二次风区向烟气区的漏风。漏风会对区域的传热和温度分布造成影响，所以在计算各个区域时，要将各漏风量加入对应区域的流量中，并考虑漏风温度的不同，然后确定各区域的流量、流速、平均温度、换热系数等。按常规处理方法，本文也将各区域的进口作为漏风点［1］。

1.3各区模型

首先考虑漏风影响对进口焓值的改变：

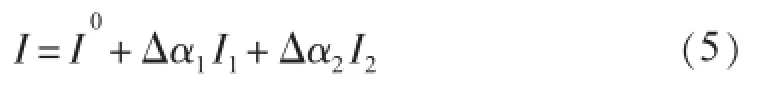
式中：I0，I分别为考虑漏风前后进口温度对应的焓值；Δα1、Δα2为相邻两区对应的漏风系数，漏进为正，漏出为负；I1，I2为相邻两区对应的平均焓值。

然后由新的焓值求出新的进口温度，再用差分替代式（3）中的微分，并用考虑漏风影响后各区流体进出口的平均温度作为流体传热温度，可得各区传热和蓄热关系式：

式中：下标n=1，2，表示沿流体方向将空预器分成2段，靠近进口段n为1，靠近出口段n为2；下标j=1，2，3，分别表示烟气区、二次风区、一次风区；αfj，n，cfj，n，ρfj，n，aj，n为第 j区第n段考虑漏风后的参数；Hj，n为第j区第n段的换热面积；tj，n-1，tj，n为第j区第n段流体考虑漏风后的进口平均温度和出口平均温度，℃；tmj，n为第j区第n段的金属受热面竖直切面的平均温度，℃；Mj，n为第 j区第 n段金属转子总的质量，kg。Wfj，n为第j区第n段在（α+Δα1+Δα2）过量空气系数下求得的流速，其中α为该区域的过量空气系数，m/s。

由于漏风影响导致质量流量变化，流速将会改变，流速的计算为：

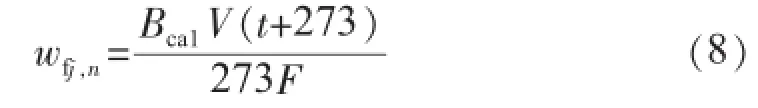
式中：Bca1为计算燃料消耗量，kg/s；V为（α+Δα1+Δα2）过量空气系数下的体积，m3/kg；t为考虑漏风后区域的平均温度，℃；F为通流截面积，m2。记：

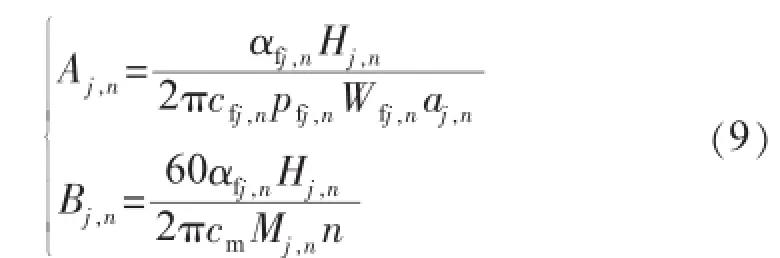
代入式（6）、（7）得各个分区所满足的关系式：

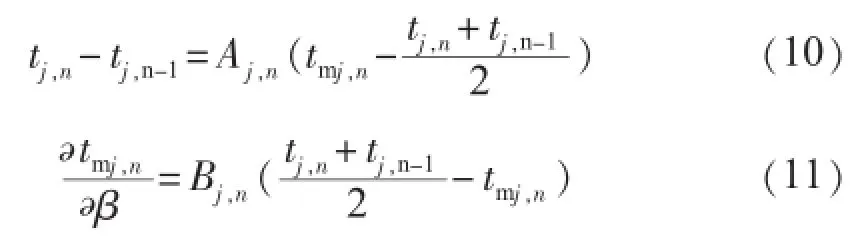
由式（10）可得到：

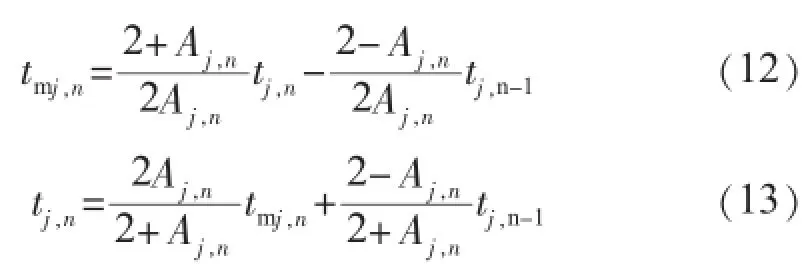
将式（13）代入式（11），可得到：

将式（14）积分得到弧度为β处的流体出口温度：

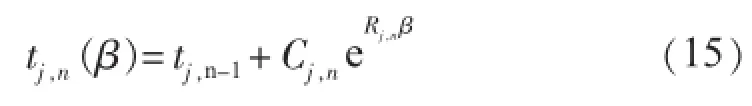
式中：Rj，n=-2Bj，n/（Aj，n+2）；Cj，n为常数。

将式（15）代入式（12）得到金属蓄热板过转子圆心的竖直切面平均温度：

由式（15）积分，可得各个分仓流体的平均出口温度为：

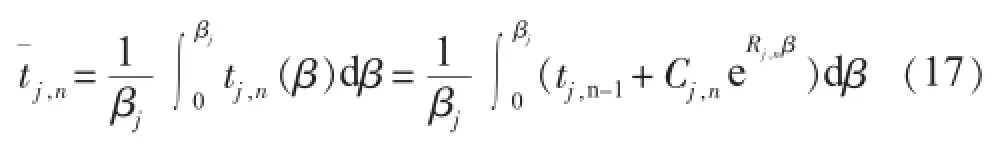
式中：βj为第j区在空气预热器中所占的弧度，rad。

若已知流体进口平均温度和出口平均温度，可将已知条件代入式（17）求解积分方程式得到常数，从而由式（16）求得金属蓄热板竖直切面进口平均温度：

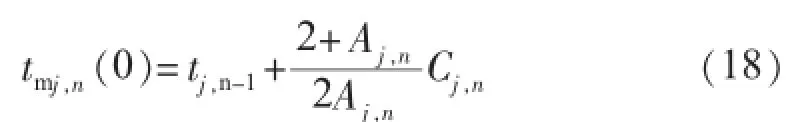
和出口平均温度：

1.4求解的唯一性

整个空气预热器共分成6个区，每个区都有3个方程，即式（14）、（15）和（16），共有18个方程。另外每个相邻区金属蓄热板温度相等，增加6个方程。这样整个空气预热器合计有24个方程。每个区都有4个未知数，即t¯j，n，Cj，n，tmj，n（0）和tmj，n（βj），共有24个未知数，与24个方程相对应，可解得唯一解。

2　计算

2.1计算步骤

根据文中计算模型，可分别对冷热段各个仓进行计算，由式（17）、（18）和（19）迭代求解出各个区流体的出口平均温度。每段的计算流程如图3所示，其总体计算步骤为：

（1）已知热段烟气进口平均温度、冷段一次风及二次风进口平均温度，假定热段、冷段烟气出口平均温度，热段、冷段二次风出口平均温度，热段、冷段一次风出口平均温度，考虑漏风影响得到新的进口温度、流速等参数，由式（17）得到常数C1，1，C1，2，最后由式（15）和式（18）得到热段、冷段烟气区金属蓄热板的

（2）按照烟气区求解的方法，得出二次风区金属蓄热板的进出口平均温度

（3）按照烟气区求解的方法，得出一次风区金属蓄热板的进出口平均温度

（4）最后将冷热段的金属蓄热板进出口平均温度进行比较，若满足：ε，则迭代结束，否则重新假定，转（1）。

2.2参数选取

（1）考虑漏风时，一次风区向烟气区和二次风区的漏风、二次风区向烟气区的漏风取设计值。在计算漏风影响时，先考虑漏风对进口流体温度、流量的影响，再按照模型计算流体出口温度及金属蓄热板温度。

图3　每段的计算流程

（2）考虑到烟气侧及空气侧的散热，文献采用与计算标准一致的方法，计算A1，n时，在其分母上乘以保温系数，即

（3）考虑到受热面污染、未完全冲刷等因素的影响，在计算换热系数αfj，n时，考虑热利用系数的影响。

（4）在计算Aj，n，Bj，n时，涉及到计算各参数，有些参数的计算在标准中没有涉及。因为烟气是由各种气体混合而成，所以烟气的部分参数计算如下：

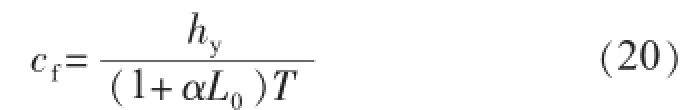
式中：hy为平均烟焓，kJ/kg；L0为完全燃烧1 kg燃料理论上需要的空气质量，kg。

式中：Gy为1 kg燃料烟气质量，kg/kg；Bj为计算燃料消耗量，kg/s。空气的部分参数如下：

其余参数可参考文献［8］计算获得。

3　计算结果及分析

文献［8］详细介绍了三分仓空气预热器的热力计算，其结果具有较好的参考性，而文献［5］在文献［8］的基础上提出了改进，所得的结果更加精确。为验证文献改进方法的可行性及计算结果的合理性，分别按照文献［8］、文献［5］和文中提出的方法，编制了三分仓热力计算程序。

算例为某1000 MW超超临界锅炉2台对称分布的三分仓空气预热器，其计算所需原始数据及3种方法的计算结果分别列于表1和表2。

表1　某1000 MW超超临界三分仓空气预热器原始数据

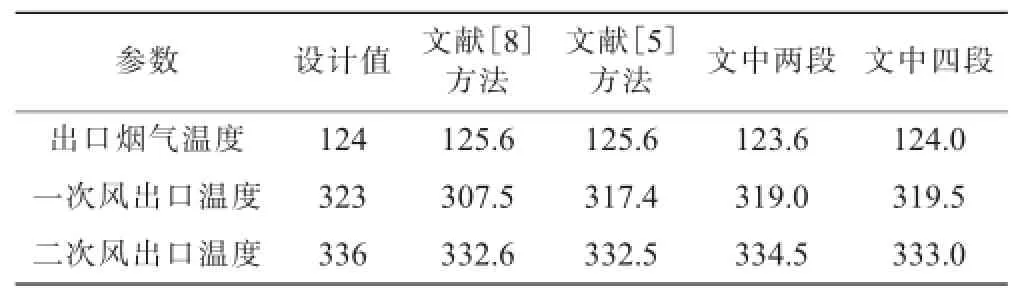
表2　算例计算结果　℃

3.1计算结果分析

由表2的计算结果及计算模型，可知文中详细热力计算方法有以下特点。

（1）具有较高计算精度。文中热力计算方法中排烟温度、一次风温度和二次风温度与设计值的差值分别为0.4℃、4℃和1.5℃，均小于文献［5］和文献［8］。因为文中方法不但考虑了金属蓄热板竖直切面平均温度沿旋转方向的非线性及流体温度的非线性特性，而且分别考虑各个漏风的影响，并且不涉及二分仓回转式空气预热器的计算方法，故文中计算方法更为合理。

（2）可以对空预器进行更加详细的划分，以满足不同的分析及设计要求。表2中可以看到：将空预器沿高度分成冷热两段共6个区域或将冷热两段再分两段得到四段共12个区域的结果差值比较小，但分成四段后可得到更多的金属和空气温度，可以根据需求划分区域得到空气预热器不同位置的温度分布。

3.2空气温度变化和金属温度分布

根据式（16）可以得到出口空气温度沿旋转方向的变化，将文中国得到的曲线与文献［5］进行比较。由图4可见：文献［5］一、二次风区的曲线斜率基本一致，即认为空气出口温度在一次风区、二次风区变化快慢一致。而文中计算方法所获得的曲线在二次风区变化快，一次风区变化较慢。因为金属蓄热板经过烟气区加热后依次经过二次风区、一次风区冷却，其在二次风区的温度较一次风区要高，二次风区的传热温差大，且二次风区的换热系数大于一次风区，所以二次风区换热更强烈，二次风区空气出口温度变化应该比一次风区要快，故文中方法的计算结果更合理。

图4　出口空气温度分布

在计算烟气、空气出口温度的同时，还能得到金属蓄热板竖直切面平均温度沿旋转方向的温度分布，图5为算例金属蓄热板竖直切面平均温度随旋转方向的变化。图中是以烟气区金属蓄热板进口为起点，温度曲线上升、水平、下降所对应β的范围分别为烟气区、密封区、空气区。在烟气、空气区内，温度变化接近线性特性。图中实线代表冷段金属蓄热板竖直切面的平均温度，为判断受热面低温腐蚀和积灰提供了理论依据。若想获得更准确的温度分布，还可以对低温段进行更详细的划分。

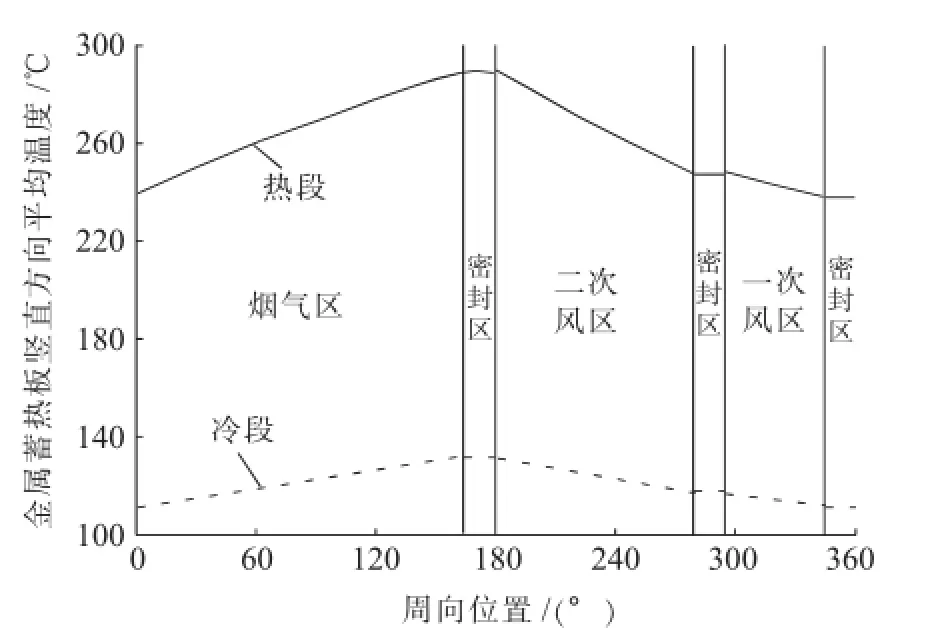
图5　金属蓄热板竖直切面平均温度分布

4　结束语

对三分仓回转式空气预热器微元体进行数学建模推导，得到了一种详细的热力计算方法，该方法根据推导的各分仓微分解析式，采用迭代计算的方法得到各分仓出口流体平均温度及金属蓄热板的平均温度。与以前介绍的热力计算方法比较，文中的热力计算方法精度较高，考虑了各分仓的漏风影响，同时能得到金属蓄热板竖直切面平均温度的分布。实际应用中，还可以划分更多计算区，得到沿烟气流动方向上不同位置处的金属和流体温度，以满足不同的分析或设计要求。

［1］北京锅炉厂译.锅炉热力计算标准方法［M］.北京：机械工业出版社，1976：86-88.

［2］周俊虎，杨卫娟，靳彦涛，等.三分仓空气预热器热力计算的研究［J］.动力工程，2003，23（6）：2810-2813.

［3］冷 伟，王 渡.一种改进的回转式空气预热器热力计算方法［J］.动力工程，2005，25（3）：392-395.

［4］WANG H Y，ZHAO L L，XU Z G，et al.The Study on Heat Transfer Model of Tri-sectional Rotary Air Preheater Based on the Semi-analytical Method［J］.Applied Thermal Engineering，2008，28：1882-1888.

［5］郑 凯，周克毅，黄军林.一种改进的三分仓空气预热器热力计算方法［J］.动力工程学报，2012，32（1）：36-40.

［6］李 杨，周元祥，谢 天，等.三分仓空气预热器热力计算的简化方法［J］.动力工程学报.2013，33（1）：37-41.

［7］陈昌贤，孙奉仲，李 飞，等.四分仓回转式空气预热器热力计算方法［J］.动力工程学报，2014，44（4）：59-63.

［8］周强泰，周克毅，冷 伟，等.锅炉原理［M］.2版.北京：中国电力出版社，2009：201-204.

A Detailed Thermal Calculation Method For Tri-sectional Rotary Air Preheaters

CHEN Huan，ZHOU Keyi，HUANG Junlin
（School of Energy and Environment，Southeast University，Nanjing 210096，China）

To improve the accuracy of thermal calculation for tri-sectional rotary air heaters，a differential element model has been set up based on the heat transfer principle of rotary air heaters and the characteristics of temperature distribution，considering the influence of air leakage.And then the analytical expressions of each sector have been obtained.At last，the fluid temperature and the mean temperature on vertical section of metallic heat accumulation plate can be calculated by means of iteration based on the analytical expressions of each sector.When 1000 MW tri-sectional regenerator is selected as computational object，the results indicate that the new method has high precision，and the calculation area can be divided as require to meet different demands of project.Also，this method can obtain the mean temperature field of the vertical section of metallic heat accumulation plate，which could provide temperature reference for analyzing low-temperature corrosion and ash deposition.

tri-sectional air preheater；differential element model；heat transfer；convection；leakage

TK222

A

1009-0665（2015）03-0010-04

2015-02-12；

2015-03-18

国家自然科学基金项目（51176031）

陈欢（1989），男，江苏无锡人，硕士研究生，从事电站锅炉特性方面研究；

周克毅（1955），男，江苏泰州人，博士生导师，从事电站锅炉方面研究；

黄军林（1986），男，山东潍坊人，博士研究生，从事电站锅炉方面研究。