基于优化遗传算法的股票选择规划研究

张金良

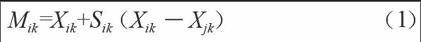
摘 要：最优股票选择规划方法在股民规避风险方面能发挥一定的作用。股市环境比较复杂，传统的股民规避风险的方法应用在实际的股市中，往往会出现主观性强、不稳定、风险大的缺点。为了避免上述问题，文章提出了优化遗传算法的股票选择规划的方法。将自适应遗传算法和贪婪算法很好的结合，获取最优的投资方向，最大限度地为股民服务。实验结果表明，利用优化遗传算法实现最优股票选择规划，可在股票发生很大波动时，很好地规避风险，防止股民产生重大损失，最终有效提高了股民的收益。

关键词：优化遗传算法;股票选择;最优规划;规避风险

中图分类号：TM714          文献标识码：A                文章编号：2095-1302（2015）09-00-03

0  引  言

股票做为风险大、收益高的债券，在现在的社会中，很多人都把自己的一部分收入做为投资投入到股市中。股市的波动时刻影响着股民的切身利益，由于股市存在极强的波动性，使得人们对股市没有很好的预测。规避风险的可能性很多，大多数股民都是通过自己的经验和小道消息来选择股票，这样带有一定的盲目性，从而给自己带来一定的投资风险[1]。

但是随着人们生活水平的不断提高，手里的闲钱也越来越多，人们更愿意把手里的闲钱投入到股市中，但目前却没有一种很好的方法来使人们规避股市风险。为了避免上述弊端，提出基于优化遗传算法[2-4]的股票选择规划方法，并对传统算法和优化遗传算法进行了比较，验证优化算法的优点。

1  股票选择规划方法原理

在股民选择股票的最优规避风险规划过程中，可以将所有的股票做为蜜源成为初始集合，在该集合中，所有元素都能代表股民选择股票规避风险过程中的解，所有解构成的集合是Xi（1，2，…，n），采用蜜蜂式搜索方式在类似区域内进行相同属性个体的搜索，重复执行搜索模式，以获取最优解。根据公式：

Mik=Xik+Sik（Xik-Xjk）                           （1）

对所有的股票选择线路进行实时跟踪监测，并对蜜源更新定位。设置j和k表示随机选取的下标，且j∈（1，2，…，A），k∈（1，2，…，e）。Sik的取值范围在[-1，1]之间，且Sik和Xik具有一定的关联性，若监测系统搜索到股市里的股票有很好的适应性，涨幅稳定，则Xik的取值范围越小。

在股民最优的股票选择中，利用公式：

（2）

可计算具有稳定性的股票占股市总体风险的概率。其中，Ti表示第i个解的稳定值。

利用公式：

Xi=Xmin+rand（0，1）（Xmax-Xmin）                  （3）

可对单个蜜源进行优化练习，重复循环直至最优解产生为止，该解替换优化之前解所在的相应位置。

为了保证股票选择路线的多样性，利用公式（3）对控制端中具有强稳定性的股市中股民对股票的选择路线进行变异处理，以便找出具有更强稳定性的选择路线。具体步骤如下：

（1）应用迭代方法，按照一定规律对旧值变量进行不断的递推，从而得到新值。设置蜜源的初始迭代次数用Q表示，且Q=0，最大迭代次数用Qmax表示，最大限制次数为L。

（2）在蜜源中随机选取N个股民的股票选择线路，并利用公式（1）计算每个股民选择股票的稳定值，根据每个股民选择股票的稳定值能够判断该解的优越性。

（3）利用公式（2）计算具有强稳定性的股民选择股票路线占总股民稳定性的概率Pi，根据概率Pi选择最优蜜源，并记录较优蜜源股票，对数据B位置进行实时更新。

（4）在仿真模型中，假如B（i）的值大于最大限制次数L的值，在解空间内进一步搜索，并记录最优解的位置，保留在监测系统中。

（5）Q+1表示在Q基础上进行一次迭代算法更新，当Q>Qmax时，记录最优蜜源代表股民选择股票路线的最优解。接着进行下一步骤操作。反之，当Q

（6）根据当前股民选择股票稳定性规划的最优解，可以很好地规避风险。

2  股民在选择股票的最优稳定性股票的方法相关理论

利用传统算法进行股市股民选择股票的最优方法的规划，建立的模型需要很多条件、耗时长。为此提出了基于优化遗传算法的股票选择规划方法。

2.1  查找股民选择最优股票的方法

根据遗传算法对股民选择最优股票的规划进行运算。遗传算法中交叉率PD和变异率PN决定股民选择最优解，表达式：

（4）

（5）

在上述表达式中，hmax表示股民在选择股票稳定性的最大适应度，havg表示股民选择股票稳定性的平均适应度，h'表示参与交叉运算的两个股民选择股票稳定性的较大的适应度，h表示经过变异处理后股民选择股票稳定性的适应度。设置j1，j2∈[0，1]，j3，j4∈[0，1]，分别表示交叉概率和变异概率的调整参数，在进行交叉运算后保留适应度最强的股票最优解。

提高计算效率，对交叉概率和变异概率进行优化处理，使Pd1>Pd2>Pd3，Pn1>Pn2>Pn3，且Pd1，Pd2，Pd3，Pn1，Pn2，Pn3∈[0，1]，可以得到如下表达式：

（6）

（7）

由上式可得，随机选取两个不同股民的股票选择路线做为交叉或者变异元素[5，6]，在进行交叉和变异计算时，当两个股民选择股票中最大的稳定度值小于当前稳定值的平均稳定度值时，对于稳定值变异或者交叉概率的选择，在最大和最小稳定度范围之间进行最优求解。

2.2  股民选取稳定值最优的股票

由于股市环境存在一定的复杂性和风险性，使得自适应遗传算法[7，8]建立的模型，具有一定的限制。而利用贪婪算法优化股民初始选择股票的稳定值，就可以帮助股民最大限度地规避风险。假设股民有m个股票选择，贪婪算法[9]的基本思想是：通过自己获得的股票上市公司的一些资讯和国家政策导向，随机选稳定值最优的股票，设为1，然后从余下（m-1）个股票选择收益最高的股票进行对比。综合各种外在条件，如果第（m-1）个股票的稳定值高于第m个股票，则用第（m-1）个股票代替第m条股票，将已经作比较的股票排除，依次进行选择，生成新的个体。

3  仿真结果分析

为了更好的验证优化遗传算法的优越性，可选取一个股民五天时间里所选股票的真实走势和优化遗传算法的预测值的误差。再利用传统算法和优化遗传算法的数据分析，就能够得到表1和表2。

表1  传统算法的数据表

时间（天） 股票真实走势（%） 传统算法预测走势（%）

周一 -3.08 2.03

周二 -7.28 4.38

周三 1.72 -6.02

周四 0.81 7.92

周五 10 0.2

表2  优化遗传算法数据表

时间（天） 股票真实走势（%） 优化算法预测走势（%）

周一 -3.08 -0.93

周二 -7.28 -5.72

周三 1.72 3.84

周四 0.81 -0.13

周五 10 8.02

通过两种方法预测股票走势和股票真实走势值之间的误差值比较，我们就可以更加清楚优化遗传算法更接近股票的真实走势。图1所示是传统算法和优化遗传算法预测值与真实值比较的误差率。

图1  传统算法和优化遗传算法预测值与真实值比较的误差率

通过比较能够很好地得出，优化遗传算法的误差值在2%以内，而传统算法的误差值不稳定，因此优化遗传算法的预测值更加接近股票的真实走势，更有利于股民很好地规避风险并获得收益的提高。

4  结  语

针对传统对于股民选择股票规划算法需求满足较多约束条件造成建模效果与真实值契合度较低的特点，提出基于优化遗传算法的股民选择最优稳定值的股票规划方法，并对传统算法和优化遗传算法做了深入的比较，在此基础上构建了新的股票选择模型。经过对于股票稳定值的最优解分析，采用优化遗传算法能更好地帮助股民规避风险，最大限度的保证了股民的利益。

参考文献

[1]邹萍.货币政策、股票流动性与资本结构动态调整[J].审计与经济研究，2015（1）：74-82.

[2]陈国良，王煦法，庄镇泉，等.遗传算法及其应用[M].北京：人民邮电出版社，1996.

[3] Back T.The Interaction of Mutation Rate，Selection and Self-Adaptation within a Genetic Algorithm[J].In：Parallel Problem Solving from Nature 2，North Holland，1992：84-94.

[4] Michalewicz Z， Janikow C Z，Krawczyk J B.A Modified Genrtic Algorithms for Optimal Control Problems[J].Computers Math Application，1992，23（12）：83-94.

[5]熊军，高敦堂，都思丹，等.变异率和种群数目自适应的遗传算法[J].东南大学学报（自然科学版），2004，34（4）：533-556.

[6]黎钧琪，石国桢.遗传算法交叉率与变异率关系的研究[J].武汉理工大学学报（交通科学与工程版），2003，27（1）：97-99.

[7]金晶，苏勇.一种改进的自适应遗传算法[J].计算机应用与软件，2006，23（2）：108-110.

[8]王晓东，薛宏智，马盈仓.基于自适应遗传算法的神经网络字符识别[J].西安工程大学学报，2008，22（2）：211-213.

[9]李少芳.连续背包问题贪婪算法最优解的实现[J].福建电脑，2003（11）：12-13.