基于PSASP的低压减载优化整定研究

先逸，刘新宇，薄其滨，李泽琦

(西南交通大学电气工程学院，四川 成都 610031)

1 引言

20世纪70年代以来，世界上相继发生了多次电压崩溃引起的大面积停电事故，比较典型的有:1983年12月27日瑞典电网、1987年1月12日法国电网、1987年7月23日日本东京电网、1996年7月2日美国西部联合电网(WSCC)等。在我国，1972年7月27日湖北电网和1973年7月12日大连电网也发生了电压崩溃事故。引起了世界各国电力工业界和学术界对电力系统电压稳定性的广泛关注[1－3]。

电压稳定研究的最终目的是开发和应用有效的控制策略来防止电压崩溃[4]。为了防止电压失稳，维持电压稳定，国内外学者提出了许多控制方法，一般分为预防控制、紧急控制和校正控制。预防控制主要包括系统规划方面的如加强输电网络，串联和并联补偿等，也包括系统运行方面的如发电机的线路压降补偿，二级电压控制等;紧急控制主要包括快速补偿装置投切，有载调压变压器紧急控制;而低压减载则属于校正控制的一种[5－6]。

低压减载被认为是防止系统发生电压崩溃的有效措施，是防止系统大面积停电、维持系统安全稳定运行的第三道防线的重要组成部分。其研究的核心问题是如何进行低压减载的整定，到目前还没有寻找到一种很好的整定方法，也没有一套完整的整定原则。通常需要考虑如下三个主要问题:(1)在什么地点安装低压减载装置;(2)低压减载装置动作电压以及相应延时如何整定;(3)切负荷量的整定[7－12]。本文基于电力系统仿真软件PSASP，在低压减载装置布点、启动电压以及延时确定的情况下，针对切负荷量的整定问题，利用分枝限界法，对现有的低压减载方案进行了优化。

2 PSASP系统建模

2.1 低压减载模型

本文以电力系统仿真软件PSASP为研究平台，采用IEEE36节点系统(如图1所示)，在负荷节点BUS9、BUS16、BUS18、BUS19、BUS20、BUS21、BUS22、BUS23、BUS29处分别装载低压减载装置。

图1 IEEE36节点系统

低压减载装置模型如图2所示。该模型使用PSASP用户自定义建模功能(UD)搭建，其中CSW1、DLY2、DYL1以及A*X1*X2模块为用户自定义建模的基本功能框，分别为可控开关1、延时2、延时1和乘法模块，对应的变量参数分别为启动电压ΔV、状态保持延时T、普通延时t和减载量K。模型可整定三轮，当输入电压与额定电压相比，差值达到了启动电压ΔV时，若该状态保持了时间T，则延迟时间t，按照预定的减载量K进行切负荷。用户可以自己设定低压减载装置每一轮的启动电压、状态保持延时、普通延时和减载量。

图2 低压减载装置模型

2.2 PSASP作业数据库及软件分析

利用PSASP检验低压减载方案的有效性需要用到PSASP的暂态稳定计算功能。设定好低压减载装置相应参数、某种运行方式以及某种故障后，进行暂态稳定计算，通过观察系统受扰后暂态电压的变化来检验该低压减载方案对该故障是否有效。在PSASP中，低压减载装置的参数、系统运行方式和故障信息均保存在相应的作业数据库和文件中(如表1所示)。通过自主研发的PSASP数据接口，应用程序可不通过PSASP软件界面直接对其修改，读取暂态稳定计算后的结果，直接调用PSASP的暂态稳定计算模块。计算模块存放于PSASP的安装文件夹WPSASP中(如表2所示)。

表1 PSASP作业数据库中部分内容

表2 WPSASP文件夹下部分功能模块

3 低压减载优化整定

3.1 分枝限界法

分枝限界法是由查理德卡普(Richard M.Karp)在20世纪60年代发明的，用于成功求解含有65个城市的旅行商问题，创当时的记录。分枝限界法把问题的可行解展开如树的分枝，再经由各个分枝中寻找最佳解[13]。

分枝限界法是组合优化问题有效求解方法，其步骤如下所述:

步骤一:如果问题的目标为最大化，则设定目前最优解的值Z=0。

步骤二:根据分枝法则，从尚未被洞悉节点(局部解)中选择一个节点，并在此节点的下一阶层中分为几个新的节点。

步骤三:计算每个新分枝出来的节点上限。

步骤四:对每一节点进行洞悉条件测试，若节点满足以下任意一个条件，则此节点可洞悉而不再被考虑:(1)此节点的上限值小于等于Z值;(2)已找到在此节点中，具最大上限值的可行解;若此条件成立，则需比较此可行解与Z值，若前者较大，则需更新Z值，将此可行解的值赋给Z，作为当前最优解;(3)此节点不可能包含可行解。

步骤五:判断是否仍有尚未被洞悉的节点，如果有，则进行步骤二，如果已无尚未被洞悉的节点，则演算停止，并得到最优解。

3.2 低压减载优化整定的分枝界限法模型

应用分枝限界法对低压减载优化整定方案进行建模。将低压减载方案设为未知变量X，根据工程实际设置M个可能的值X(n)(n=1，2，…，M)。设低压减载方案X(n)能适应的故障数为A，在某种运行方式的某种故障下，低压减载后全网所有母线的稳态电压均能恢复至0.9～1.05p.u.内，则对A加1。设低压减载方案X(n)的总体切负荷量为D，D为在每种运行方式下的每个故障下全网低压减载切负荷总量之和。

对于任一给定的X(n)(如某一确定的低压减载方案)，为了得到目标函数值A，需要进行s次动态仿真(s为可能发生的故障总数)，计算s组减载量并相加得到D，如果对所有的X值都进行仿真计算，将需要进行s×M次，这将需要耗费大量时间。因此，为提高求解速度，定义低压减载方案X(n)的不适应故障数B，对求解过程剪枝。对于某一确定的低压减载方案X(n)，在某种运行方式的某种故障下，低压减载后有母线的稳态电压不能恢复至0.9～1.05p.u.内，则对B加1，在B＞2的条件下舍弃该解，不用将所有故障都计算完。具体求解过程如图3所示。

图3 基于分枝限界法的低压减载整定

3.3 优化整定的实现

根据上述思想，对某一确定低压减载方案，通过自主研发的PSASP数据接口在udlib.dst文件中修改低压减载模型的相应参数，在case_st和dist_inf中修改相应的运行方式和故障信息，通过自主研发的PSASP计算接口，调用暂态稳定计算模块进行计算，计算完毕后从表stana(x)中获取全网稳态电压的最低值和最高值，用以判断当前方案对该工况下该故障是否适用，更新A的值。同时从表usto(x)中获取各个节点的减载量并相加，更新D的值。在此过程中，若B＞2，则跳出循环，否定当前方案。所有工况下的所有故障均计算完毕，则比较当前A的值和历史最佳A的值Amax，若A小于Amax则否定当前方案;若A值等于Amax则比较当前D的值和Dmin，若D小于Dmin，则将该方案作为当前最佳方案，用A和D更新Amax和Dmin，反之则否定该方案;若A值大于Amax，则将该方案作为当前最佳方案，用A和D更新Amax和Dmin。换下一组解重复上述步骤，直到算完所有可行解得出最优解。优化整定具体流程如图4所示。

4 算例验证

算例基于IEEE36节点系统，定义两种运行方式。方式一，发电机有功出力为2618MW，无功出力为1256MW，有功负荷为 2567.8MW，无功负荷为1157.6MW，选取6种典型故障，如表3所示;方式二，发电机有功出力为2458MW，无功出力为1170MW，有功负荷为2373.2MW，无功负荷为1089.6MW，选取4种典型故障，如表4所示。

低压减载方案分为三轮，启动电压分别为0.92、0.88、0.84(p.u.)，保持时延均为0，普通时延均为0.2s。通过优化整定，得出各轮次最优减载量分别为16.8% 、11.2% 、6.9% 。

方案一为不采用低压减载装置;国内低压减载方案通常将减载量均分到各轮次，减载量通常选择最大负荷的30% ～50%，故设方案二，减载量设定为30%，每轮10%;方案三，减载量设定为45%，每轮15%;方案四，采用本文优化出的低压减载方案。

如表5所示，通过方案一和方案四对比，在9种故障下，电网的自愈能力都不足以使全网最低电压恢复到0.9 p.u.以上;而方案四，在所有故障情况下，均能使全网最低电压恢复到0.9 p.u.以上，证明了该方案的有效性。图5、图6分别为故障3和故障10下，未采用方案一和方案四全网最低电压的波形对比图。

图4 优化整定流程图

表3 方式一下典型故障

表4 方式二下典型故障

表5 故障后各种方案下最低稳态电压对比

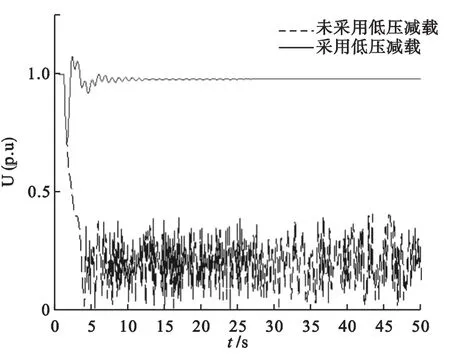
图5 故障3下的电压波形

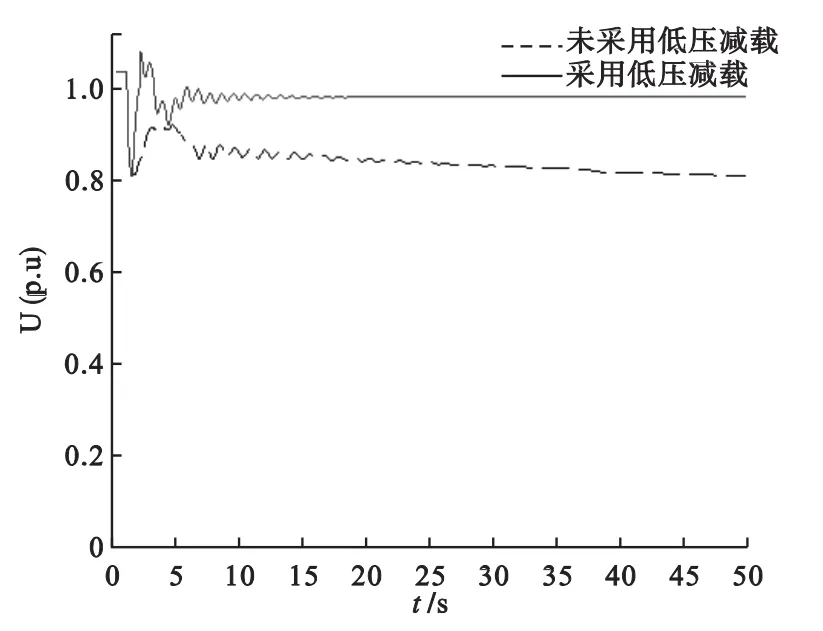
图6 故障10下的电压波形

如表5所示，通过方案二和方案四对比，在故障1、2、8下，方案二不能使全网最低电压恢复到0.9 p.u.以上，且所有故障下，低压减载装置动作切除的总负荷量为2525MW，表明该方案在某些故障下存在一定的欠切。通过方案三和方案四对比，在所有故障下全网最低电压都能恢复到0.9 p.u.以上，但切除的总负荷量为3335MW，而方案四切除的总负荷量为3008.89MW，表明方案三存在一定的过切。方案四既满足了所有故障下电压的要求，同时总切负荷量降到了最低，充分证明了该方案的优越性。

5 结论

本文在PSASP IEEE36节点系统上搭建了低压减载模型，并通过自主研发的PSASP数据接口和计算接口，成功修改低压减载模型参数，直接调用和控制PSASP暂态稳定计算模块，实现了通过PSASP暂态稳定计算校验低压减载方案有效性的程序控制。

提出了基于分枝限界法的低压减载优化方案。通过与已有低压减载方案的对比分析，基于分支限界法的低压减载优化方案，能在满足电压稳定的前提下，使得切负荷量最小，具有一定的优越性和工程实用价值。

[1]苑画舫.北京电网低压减载方案研究[D].华北电力大学(河北).2008.

[2]马世英，易俊，孙华东，等.电力系统低压减载配置原则及方案[J].电力系统自动化，2009，33(5):45 －49.

[3]TAYLOR，W C.Concepts of under－ voltage load shedding for voltage stability[J].0，7(2):480 －488.

[4]王永辉.电力系统低压减载的整定方式研究[D].重庆大学，2007.

[5]孙光辉，沈国荣.加强三道防线建设确保电网的安全稳定运行(摘要)[J].电力安全技术，2004(7).

[6]薛禹胜.时空协调的大停电防御框架 (一)从孤立防线到综合防御[J].电力系统自动化，2006，30(1):8 －14.

[7]马平，蔡兴国，于继来，等.基于最小不匹配函数的低压减载算法研究[J].中国电机工程学报，2005，25(1):27 －31.

[8]BALANATHAN，R.Under-voltage load shedding to avoid voltage instability[J].0，145(2):175 －181.

[9]刘斌，陈磊，闵勇.考虑暂态电压稳定的低压减载地点选择[J].电力系统自动化，2008，32(5):11 －14.

[10]戴剑锋，朱凌志，周双喜，等.基于风险的低压减载策略问题研究[J].中国电机工程学报，2006，26(19):18 －22.

[11]黄镔，赵良，马世英，等.基于PV曲线的低压减载配置方法[J].电网技术，2008，32(23):29 －34.

[12]袁宇春，张保会.最佳切负荷时刻的计算[J].继电器，1999，27(6):1－4.

[13]王凌.智能优化及其应用[M].北京:清华大学出版社，施普林格出版社，2001.