四边支承预应力混凝土双向板内力重分布

王晓东，郑文忠，王 英

(1.结构工程灾变与控制教育部重点实验室(哈尔滨工业大学)，150090哈尔滨;2.哈尔滨理工大学建筑工程学院，150001哈尔滨)

GB50010、JGJ92和ACI318等国内外设计规范关于无粘结筋应力增量的计算和弯矩调幅设计都是针对单向受力梁板提出的，四边支承预应力混凝土双向板中无粘结筋应力增量的计算及这类板的弯矩调幅计算未见相关报道［1-4］.由于四边支承混凝土双向板中非预应力筋受拉屈服后形成的塑性铰线区别于单向塑性铰，且板中各位置处的无粘结筋应力增量也不相同，因此对四边支承无粘结预应力混凝土双向板应用预应力混凝土连续梁中的无粘结筋应力增量及弯矩调幅系数计算公式进行内力重分布设计将产生较大偏差.而无粘结预应力混凝土双向板内部受力复杂，一般方法很难对全过程分析达到理想精度.因此本文采用ABAQUS有限元软件建立了四边支承无粘结预应力混凝土双向板精细化模型，该模型充分考虑了材料的非线性以及无粘结预应力混凝土结构的特点，可深入揭示无粘结筋应力变化、滑移效应、内力重分布、结构塑性变形等复杂特性.基于有限元分析结果，建立了正常使用阶段和承载能力极限状态下预应力混凝土双向板中无粘结筋应力增量计算式，以及弯矩调幅系数计算表达式.

1 有限元模型的建立

ABAQUS有限元软件，具有 Standard和Explicit两个分析模块［5］.本文利用 Standard 分析模块对预应力混凝土结构的塑性性能进行有限元分析.

1.1 有限元模型的建立过程

无粘结预应力混凝土双向板有限元模型的主要单元为混凝土板壳单元和非预应力筋与预应力筋桁架单元.板壳和桁架的端部节点用ABAQUS的内在约束MPC连接，为模拟无粘结筋和混凝土之间没有粘结作用可产生相对滑动的特点，将无粘结筋和混凝土节点间设置刚性弹.无粘结筋预应力的建立通过“降温法”来实现.即在 initial condition中定义温差，使预应力作用下板静态平衡后桁架单元的应力值与实际有效预应力一致［6］.

1.2 单元选择

本文采用8节点六面体线性减缩积分单元“C3D8R”来模拟混凝土板，该单元具有位移结果精确的优点.为防止产生沙漏，沿板厚方向划分4个单元.非预应力筋和无粘结筋采用桁架单元“T3D2”模拟，该单元为在空间中只能承受拉伸和压缩荷载作用的线状构件.

1.3 材料本构关系

1.3.1 混凝土本构模型

国内外学者提出了多种考虑混凝土塑性性能的本构模型，本文在ABAQUS分析中对混凝土采用可考虑材料拉压性能的损伤塑性模型.

对于单轴向混凝土本构模型，本文采用过镇海等［7］提出的混凝土单轴受拉和受压应力-应变曲线(图2).该应力-应变曲线在应力峰值点处导数连续，可根据不同材料对曲线进行调整，适合本文对预应力混凝土结构的精细化分析，模型应力、应变方程可采用过镇海［7］提出的相关公式.对于混凝土多轴应力应变关系，采用江见鲸等［8］提出的模型方程，屈服条件采用由Lublinear等［9］提出的模型方程，在混凝土损伤塑性模型中的塑性势面采用Drucker等［10］提出的静水压力面.

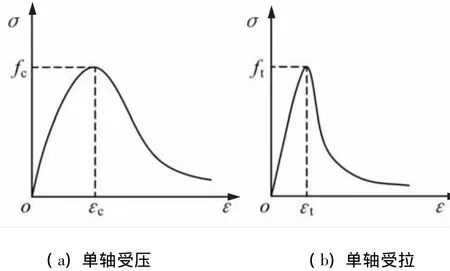
图1 混凝土单轴应力-应变曲线

1.3.2 预应力筋与非预应力筋本构模型

非预应力筋采用图2所示的理想弹塑性本构模型，预应力筋本构关系采用三折线模型.

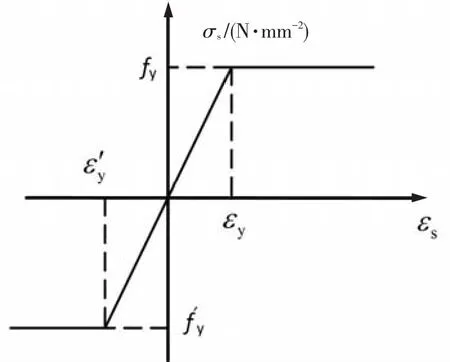
图2 钢材的本构关系

2 模型验证

2.1 双向板模型试验

大连理工大学宋永发等［11］进行了2块四边简支的无粘结预应力混凝土双向板(编号WB-1、WB-2)的试验研究，双向板模型尺寸为4 200 mm×4 200 mm，板厚100 mm.所用混凝土强度等级为C30，预应力筋为fptk=1 860 MPa的φs5高强钢丝，张拉控制应力为(0.60～0.65)fptk．非预应力筋按φ6.5@200双层双向均匀布置，屈服强度实测值为321.6 MPa.试件各材料强度实测平均值及其他参数见表1.该双向板模型采用16个点的集中荷载模拟均布荷载.

表1 试件基本数据

2.2 试验结果分析

由有限元模型分析得到的双向板荷载-跨中最大变形曲线与试验曲线的对比见图3.双向板在加载过程中跨中变形的有限元分析结果与实测值吻合较好，说明本文建立的有限元模型具有一定的计算精度.

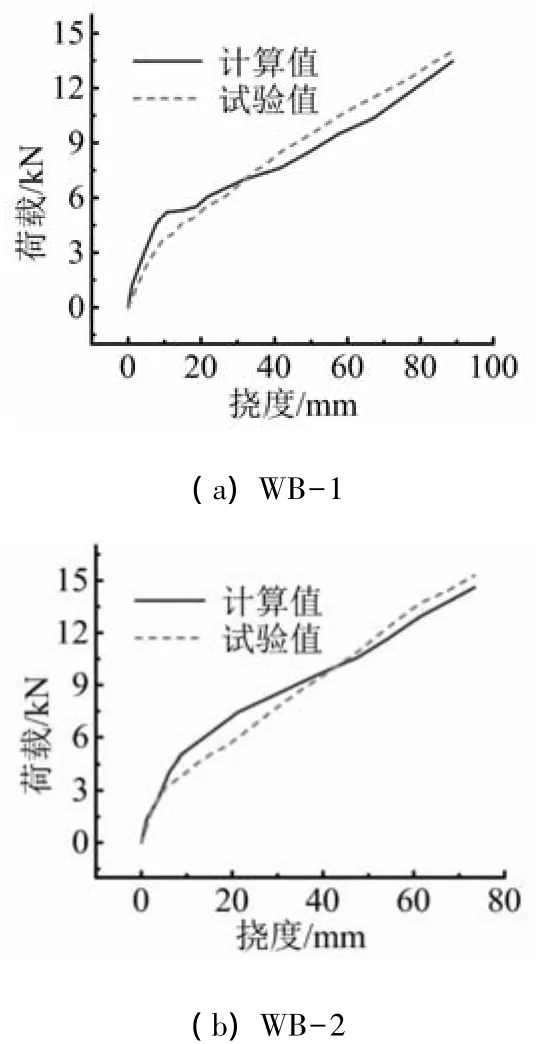
图3 板中心变形的试验值与计算值对比

3 双向板设计

3.1 荷载确定

3.1.1 恒载

本文无粘结预应力混凝土双向板设计中考虑的恒荷载见表2.

表2 恒载统计

3.1.2 活载

参见GB5009—2012《建筑结构荷载规范》中表4.1.1，可以发现活荷载标准值在2～5 kN/m2范围分布最多.从适应实际工程应用考虑出发，四边支承无粘结预应力混凝土双向板的模型设计均考虑了活荷载分别为2、3、4、5 kN/m2时的情况.

3.2 板厚确定

根据工程经验，无粘结预应力混凝土双向板的跨度一般在7～10 m内，故本文设计的双向板模型中，板的跨度有 7、8、9、10 m 共 4种类型.每种跨度下的板厚可由最小高跨比1/45确定.

3.3 混凝土及钢筋材料的确定

各双向板模型中预应力筋采用抗拉强度标准值fptk=1 860 N/mm2的φs5无粘结预应力钢丝，混凝土强度等级为 C40(μfcu=49.8 N/mm2)，弹性模量Ec=3.25×104N/mm2.

对于非预应力筋，本文根据中国近年颁布的GB 50010—2010《混凝土结构设计规范》及GB1499.2—2007《钢筋混凝土用热轧带肋钢筋》国家标准，将双向板的模型设计考虑了非预应力筋钢 种 分 别 为:HPB300、HRB335、HRB400、HRB500及HRB600时的情况.

3.4 双向板模型设计

四边支承无粘结预应力混凝土双向板按其边界条件可分为6类:四边简支、四边固支、两临边简支两临边固支、三边固支一边简支、三边简支一边固支、两对边简支两对边固支［12-13］.其中四边支承双向板模拟独立的四边墙支承和梁支承双向板;四边固支双向板模拟内区格板;两临边简支两临边固支双向板模拟角区格板;三边固支一边简支双向板模拟边区格板;三边简支一边固支双向板模拟一方向连续、一方向单跨的端区格板;两对边简支两对边固支双向板模拟一方向连续、一方向单跨的中区格板.它们基本涵盖了所有边界支承条件的双向板类型.根据各四边支承条件下的双向板在不同外载下的弹性内力计算值，可分别进行配筋设计.

4 双向板中无粘结筋应力增量计算

4.1 无粘结筋应力增量计算

为尽量减少有限元分析过程中双向板中预应力筋的应力误差，并考虑到已验证双板的有限元变形分析结果与实测结果拟合程度较好，本文通过无粘结筋在双向板受荷后的整体变形求得其应力增量值.大体思路是由双向板中无粘结筋的变形前后节点坐标进行曲线拟合，通过弧长积分得到其变形前后的长度差值即无粘结筋伸长值，进而根据本构关系确定无粘结筋的应变及应力增量［14］.

本文预应力混凝土双向板为均匀配置预应力筋，这是因为“均匀布筋”、“中密边疏”、“仅中间分布”等布筋形式的双向板中无粘结筋应力增量是不同的，而基于均匀布筋得出的结论用于其他情况是偏于安全的.为方便计算，本文将四边不同支承条件下的双向板跨中最大变形所在截面所对应的无粘结筋应力增量做为基本考察对象并建立相应的无粘结筋应力增量计算公式，进而探索板中任一截面处的无粘结应力增量与板中最大变形截面处无粘结筋应力增量的关系式.

4.2 正常使用阶段无粘结筋应力增量

以预应力混凝土双向板控制截面受拉非预应力筋屈服做为正常使用极限状态的标志，基于有限元模型分析结果，可得到正常使用极限状态下与四边不同支承条件相对应的以单位板宽综合配筋指标为自变量、以板跨中最大变形处无粘结筋应力增量Δσpy为因变量的关系曲线．以配有HRB400级非预应力筋的双向板为基础，以四边简支和四边固定双向板为例，β0-Δσpy计算结果见图4．

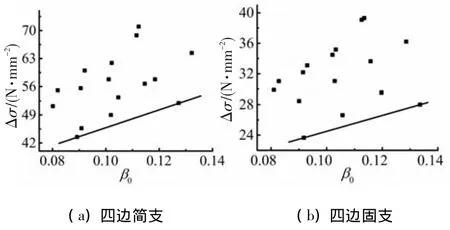
图4 Δσpy与β0的拟合曲线

从图4可看出，在正常使用极限状态下，与双向板跨中最大变形处所对应的无粘结筋应力增量Δσpy随着综合配筋指标β0的增大而增大．这是因为综合配筋指标β0反映了预应力筋与非预应力筋对截面抗弯承载力的综合影响，在正常使用阶段，随着双向板中β0的增大，截面抗弯承载力提高，推迟了双向板控制截面非预应力筋的受拉屈服，给双向板的弯曲变形留下了较大空间．

各四边支承条件下双向板数据点的下包线做为非预应力筋为HRB400的预应力混凝土双向板中无粘结筋应力增量ΔσpyHRB400计算式的拟合曲线，可由式(1)表达:

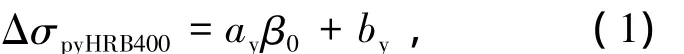
式中系数ay、by与四边支承条件相关，取值见表3．

表3 正常使用阶段无粘结筋应力增量计算系数

为考察非预应力筋钢种对无粘结筋应力增量的影响，令μpy为在综合配筋指标等基本参数相同的情况下分别配有HPB300、HRB335、HRB500和HRB600非预应力筋的双向板与配有HRB400非预应力筋的双向板在正常使用极限状态下无粘结筋应力增量的比值.则非预应力筋抗拉屈服强度fy与μpy关系见图5．

取图5中数据点的下包线得非预应力筋钢种影响系数μpy为

图5 μpy与 fy关系

则配置任一非预应力筋钢种的无粘结预应力混凝土双向板跨中最大变形处无粘结筋在正常使用极限状态下的应力增量Δσpy为

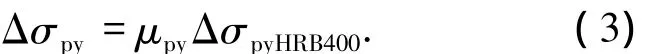
4.3 承载力极限状态无粘结筋应力增量

以预应力混凝土双向板受压区外边缘混凝土达到极限压应变做为承载能力极限状态标志.基于有限元模型分析结果，可得到在承载能力极限状态下与四边不同支承条件相对应的以单位板宽综合配筋指标β0为自变量、以板跨中最大变形处无粘结筋应力增量Δσpu为因变量的拟合曲线．以配有HRB400级非预应力筋的双向板模型为基础，以四边简支和四边固定双向板为例，Δσpu-β0计算结果见图6．

图6 Δσpu与β0的拟合曲线

从图6可看出，在承载能力极限状态下各支承条件下的双向板中无粘结筋应力增量Δσpu都随着β0的增大而减小．这是因为随着β0的增大，也即预应力筋与非预应力筋配筋量的增加，使得预应力混凝土双向板延性降低，配筋较多的双向板在承载能力极限状态塑性铰线发展要明显低于配筋较少的双向板，从而影响了无粘结筋极限应力增量．

分别取各四边支承条件双向板数据点的下包线做为非预应力筋为HRB400的预应力混凝土双向板中无粘结筋应力增量ΔσpuHRB400计算式的拟合曲线，可由式(4)表达:

式中系数au、bu与四边支承条件相关，取值见表4．

表4 承载能力极限状态无粘结筋应力增量计算系数

为考察非预应力筋屈服强度对双向板中无粘结筋应力增量的影响，令μpu为在单位板宽综合配筋指标等基本参数相同的情况下分别配有HPB300、HRB335、HRB500 和 HRB600 非预应力筋的双向板与配有HRB400非预应力筋的双向板在承载能力极限状态下无粘结筋应力增量的比值.则根据有限元模拟计算结果，可得到与非预应力筋抗拉屈服强度fy对应的μpu关系，见图7．

由图7可知，随着非预应力筋屈服强度的提高无粘结筋极限应力增量有所增大.取图7中数据点的下包线得到μpu的方程曲线为

则在承载使用极限状态下，配置任一非预应力筋钢种的预应力混凝土双向板跨中最大变形处无粘结筋应力增量Δσpu为

图7 μpu与 fy关系

4.4 任意截面无粘结筋应力增量计算

由式(3)、(6)可分别得到在正常使用和承载能力极限状态下双向板最大变形处无粘结筋应力增量.由于双向板变形的不均匀性，其他截面处无粘结筋应力增量将小于该值，因此无粘结筋应力增量应与其在板中的位置相关.由此引入无粘结筋分布系数η来考虑这一问题，η定义为:某一方向编号为i的无粘结筋至与其平行的固支边最短距离li与该固支边边长l之比．若与该无粘结筋平行的两边都为简支边，则li为该无粘结筋至与其平行简支边的最短距离，l为该简支边边长．同时，令该无粘结筋应力增量Δσpi与板内同一方向无粘结筋最大应力增量Δσpmax之比为κ．

由有限元分析结果，可分别确定在正常使用极限状态和承载能力极限状态下与不同支承条件对应的双向板中无粘结筋分布系数η与应力增量比例系数κ的关系曲线，并由此得到κ的计算公式．

4.4.1 正常使用极限状态κs的计算公式

以四边简支和四边固定双向板为例，正常使用极限状态下预应力混凝土双向板中各无粘结筋分布系数η与应力增量比例系数κs的关系曲线见图8．由于双向板的变形沿两方向中心线对称，因此仅取一半曲线进行考察．

图8 η与κs的拟合曲线

图8中若与所考察无粘结筋平行的两板边支承情况相同，由于双向板在该方向的变形沿中心线对称，因此仅给出一半的κs-η曲线.

正常使用极限状态下与各支承条件相对应的以分布系数η为自变量的应力增量比例系数κs计算式见式(7)～(15).

四边固支双向板:

四边简支双向板:

三边固支一边简支双向板:

两边固支方向

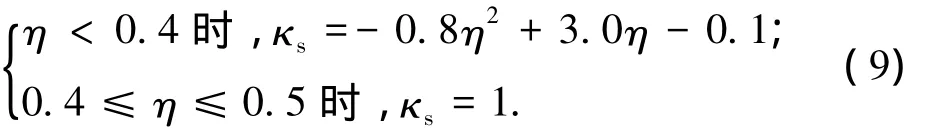
一边固支一边简支方向

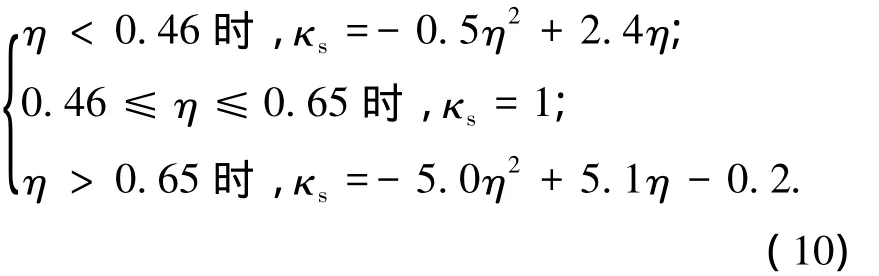
三边简支一边固支双向板:

两边简支方向

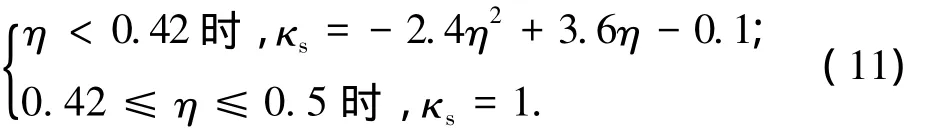
一边简支一边固支方向

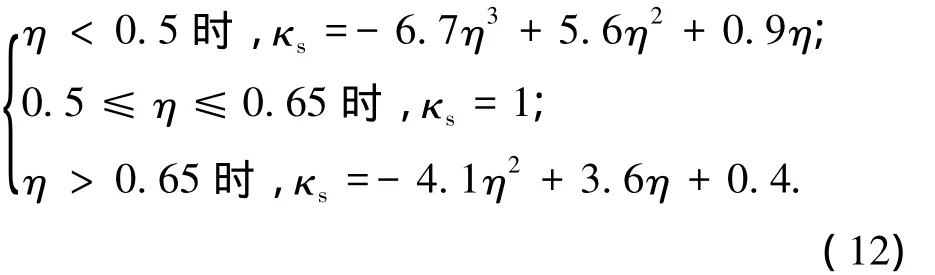
两对边固支两对边简支双向板:

两边简支方向

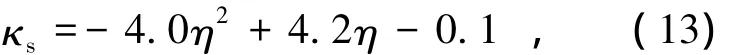
两边固支方向

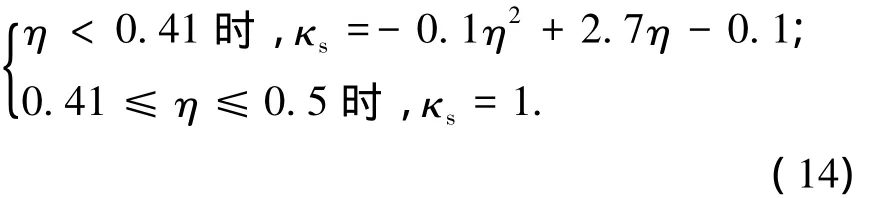
两临边固支两临边简支双向板:

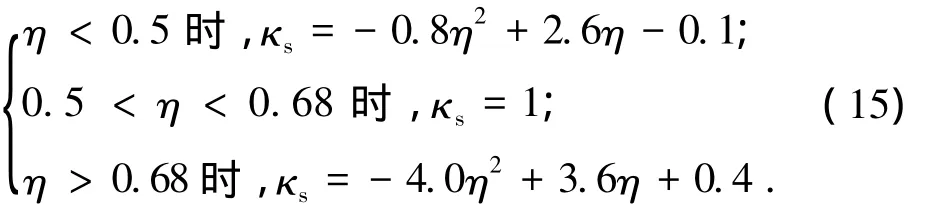
4.4.2 承载能力极限状态κu的计算公式

以四边简支和四边固定双向板为例，承载能力极限状态下各支承条件下预应力混凝土双向板中各无粘结筋分布系数η与应力增量比例系数κu的关系曲线见图9．由于双向板的变形沿两方向中心线对称，因此仅取一半曲线进行考察．

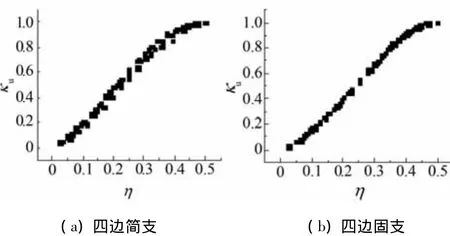
图9 η与κu的拟合曲线

则承载能力极限状态下与各支承条件相对应的以分布系数η为自变量的应力增量比例系数κu计算式见式(16)～(24)．

四边固支双向板:

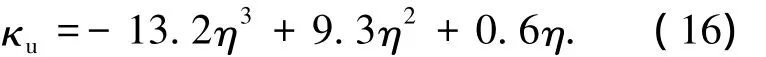
四边简支双向板:

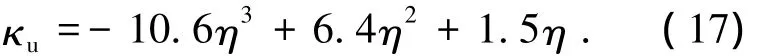
三边固支一边简支双向板:

两边固支方向

一边固支一边简支方向

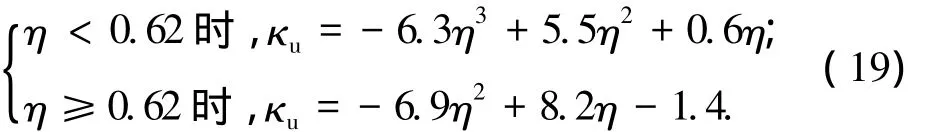
三边简支一边固支双向板:

两边简支方向

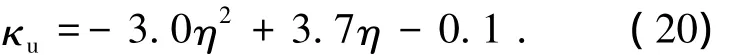
一边简支一边固支方向

两对边固支两对边简支双向板:

两边简支方向

两边固支方向

两临边固支两临边简支双向板:

4.5 双向板中无粘结筋应力增量公式

综上所述，可得到预应力混凝土双向板中两方向任一编号为i的无粘结筋在正常使用极限状态及承载能力极限状态下的应力增量公式:

正常使用极限状态下无粘结筋应力增量计算公式为

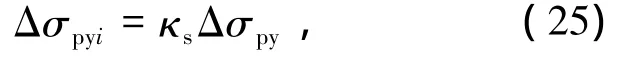
式中:Δσpyi为编号为i的无粘结筋在正常使用极限状态下的应力增量，κs根据四边支承条件由式(7)～(15)确定，Δσpy由式(3)确定．

承载能力极限状态下无粘结筋应力增量计算公式为

式中:Δσpui为编号为i的无粘结筋在承载能力极限状态下的应力增量，κu根据四边支承条件由式(16)～(24)确定，Δσpu由式(6)确定．

5 双向板内力重分布设计

5.1 四边支承双向板的弯矩调幅系数

与预应力混凝土连续梁相似，预应力混凝土双向板在加荷过程中截面刚度不断变化，支座截面次弯矩的大小也随之变化.从公式实用性角度出发，以双向板支座各截面的外载弯矩Mload与张力引起的次弯矩之和Msec(Mload+Msec)为调幅对象是比较合适的，可与双向板弹性设计方法相协调．由于双向板各截面弯矩不均匀，因此在分析时取支座处的总弯矩作为调幅对象．

5.2 参数分析

5.2.1 跨高比的影响

由于无粘结预应力混凝土双向板的常用跨高比范围1/40～1/45相差不大，且经分析在此范围内跨高比对预应力混凝土双向板弯矩调幅影响不大，因此暂不考虑跨高比的影响.

5.2.2 综合配筋指标的影响

以受压区外边缘混凝土达到极限压应变作为预应力混凝土双向板的破坏标志，根据分析数据可得到连续板支座处板跨宽度范围内总弯矩的有限元分析结果相对弹性计算结果的调幅幅度α．取双向板综合配筋指标β0为自变量，可得到如图10所示的连续双向板支座控制截面弯矩调幅系数α随综合配筋指标β0变化的关系图．随着综合配筋指标的增加，弯矩调幅系数随之减小．由此可看出双向板的弯矩调幅系数随综合配筋指标β0的变化趋势规律与单向板相似，即随着综合配筋指标的增加支座截面的弯矩调幅系数有较为明显的降低．这是由于预应力筋及非预应力筋用量的增加虽可提高截面的抵抗弯矩，但塑性铰线转动能力随之下降，使得弯矩调幅能力有较为明显的下降趋势．

5.2.3 预应力度的影响

为进一步考察在综合配筋指标一定的情况下预应力度对弯矩调幅系数的影响，对原四边固支双向板模型中的预应力筋与非预应力筋用量进行了调整，使之在综合配筋指标不变的情况下预应力度λ分别控制在0.5、0.6、0.7、0.8四个等级进行分析，不同综合配筋指标β0下双向板支座截面弯矩调幅系数α随λ的变化曲线见图11．在综合配筋指标β0相同的情况下改变预应力度对双向板弯矩调幅影响不大．由此可见虽然预应力度较大的双向板由于无粘结筋比例的增加使得支座控制截面延性降低，但非预应力筋比例的降低同时使得支座控制截面延性提高．总体上弯矩调幅系数α变化不明显，因此在弯矩调幅系数计算公式中不计入预应力度的影响．

图10 α与β0关系

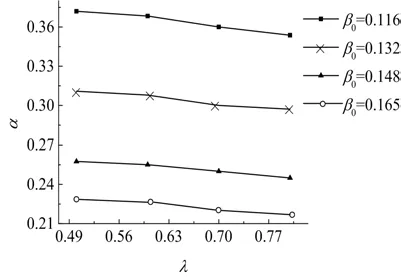
图11 α与λ关系

5.2.4 非预应力筋钢种的影响

为考虑非预应力筋钢种对无粘结预应力混凝土双向板弯矩调幅系数α的影响，令μs为在单位板跨综合配筋指标等基本参数相同的情况下分别配有 HPB300、HRB335、HRB500和 HRB600 级非预应力筋的双向板与配有HRB400级非预应力筋的双向板弯矩调幅系数的比值.则根据有限元模拟计算结果，可得到如图12所示与非预应力筋抗拉屈服强度fy对应的μs关系图．不同预应力筋钢种对弯矩调幅系数α的影响较为明显，且随着非预应力筋强度等级的提高而呈下降趋势．

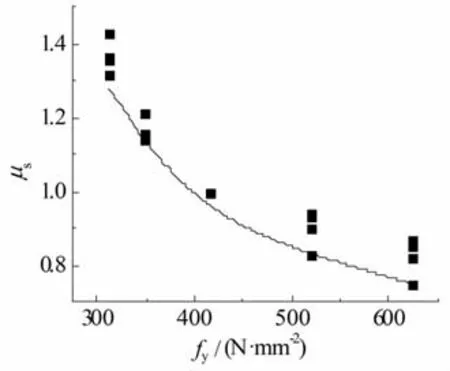
图12 μs与fy关系

5.3 弯矩调幅系数计算公式的建立

综上所述，影响无粘结预应力混凝土双向板弯矩调幅系数的主要参数应为综合配筋指标β0和非预应力筋钢种．以配有HRB400级非预应力筋的无粘结预应力混凝土双向板弯矩调幅系数αHRB400的函数表达式做为基本公式，由图10可得αHRB400函数表达式为

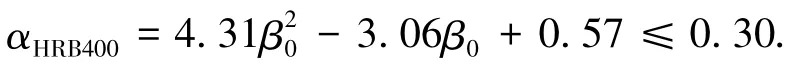
考虑到若调幅过高将造成双向板产生过度塑性变形，难以保证正常使用阶段的挠度及裂缝宽度限制要求，因此建议最大调幅幅度为0.30.

对配有其他强度等级非预应力筋的无粘结预应力混凝土双向板，弯矩调幅系数α可表达为非预应力筋钢种影响系数μs与基本计算式αHRB400乘积的形式:

取图12中数据的下包线作为非预应力筋钢种影响系数μs的方程曲线:

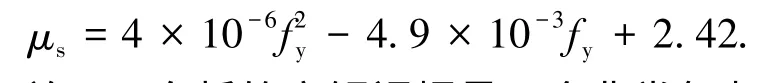
关于双向板的弯矩调幅是一个非常复杂的问题，本文仅对四边固结双向板的弯矩调幅进行了计算分析，未涉及边区格板和角区格板.

6 结 论

1)提出了各类四边支承预应力混凝土双向板中无粘结筋应力增量的计算公式和弯矩调幅设计计算方法.

2)建立了随综合配筋指标β0增大而增大，随非预应力筋屈服强度提高而提高的正常使用阶段无粘结筋应力增量计算公式，和随综合配筋指标β0增大而减小，随非预应力筋屈服强度提高而增大的承载能力极限状态无粘结筋应力增量计算公式．

3)建立了四边支承预应力混凝土双向板固结边负弯矩调幅系数计算公式，该调幅系数随综合配筋指标β0增大而减小，随非预应力筋屈服强度提高而减小．

［1］LIU B，SONG M，JIANG Y，et al.Experimental study on seismic performance of post-tensioned precast prestressed concrete frame［J］.Journal of Building Structures，2011，32(2):24-32.

［2］LIU J S.Design analysis of unbonded prestressed concrete two-way slab［J］.Applied Mechanics and Materials，2012，204:853-856.

［3］FU Q，JIN L Z，ZHOU H M，et al.Brief analysis on the mechanical behavior influenced by opening locations of the unbonded prestressed concrete slabs［J］.Advanced Materials Research，2011，243:774-778.

［4］GUIGLIA M，DEBERNARDI P G，TALIANO M.Calculation of the ultimate stress of unbonded tendons in prestressed concrete members considering the rotation capacity［J］.Magazine of Concrete Research，2012，65(1):14-26.

［5］王素裹，韩小雷，季静.ABAQUS显式分析方法在钢筋混凝土结构中的应用［J］.科学技术与工程，2009，9(16):4688-4692.

［6］楼铁炯.无粘结预应力梁的有限元建模与性能分析研究［D］.杭州:浙江大学，2005.

［7］过镇海.混凝土的强度和变形-试验基础和本构关系［M］.北京:清华大学出版社，1997.

［8］江见鲸，陆新征，叶列平.混凝土结构有限元分析［M］.北京:清华大学出版社，2005.

［9］LUBLINER J，OLIVER J，OLLER S，et al.A plasticdamage model for concrete.international［J］.Journal of Solids and Structures，1989，25(3):299-326.

［10］DRUCKER D C，PRAGER W.Soil mechanics and plastic analysis or limit design［J］.Quarterly of Applied Mathematics，1952，10:157-165.

［11］宋永发，王清湘，宋玉普，等.无粘结预应力双向板变形计算方法研究［J］.大连理工大学学报，2001，41(5):617-620.

［12］FARGHALY A S，UEDA T.Prediction of punching shear strength of two-way slabs strengthened externally with FRP sheets［J］.JournalofCompositesfor Construction，2010，15(2):181-193.

［13］GALES J，BISBY L A，GILLIE M.Unbonded post tensioned concrete slabsin fire-partI-experimental response of unbonded tendons under transient localized heating［J］.Journal of Structural Fire Engineering，2011，2(3):139-154.

［14］周威.预应力混凝土结构设计三个基本问题研究［D］.哈尔滨:哈尔滨工业大学，2005.