无功补偿电容器组参数在线辨识方法

牛胜锁，梁志瑞，苏海锋，赵 飞

（华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003）

0 引言

电力系统中并联电容器组向系统提供无功补偿，提高节点电压，减少线路损耗。同时，为了限制合闸涌流及起到一定的谐波滤除作用，往往在电容器组中串联一定电抗率的电抗器。电容器组的正常运行对电力系统的安全稳定十分重要，因此，一般每年都要安排对其进行预防性试验，检测电容器组各项参数是否正常。进行预防性试验时，测量电容器需拆除连接线，不仅工作量大而且易损坏电容器。目前，也有专门的电力电容器电容量测试仪，测量时不需拆除电容器的连接线，但也要停电加信号进行测试[1]。电容器组参数的在线辨识可避免以上问题，同时，还可以在线分析电容器组的并联谐振问题[2-4]及其有功损耗情况[5]，为实现设备的状态检修及智能电网的建设提供帮助。

本文对电容器组参数的在线辨识方法进行了研究，建立电容器组的基波及谐波模型，提出了通过同步测量投运电容器组的电压、电流，利用加窗插值快速傅里叶变换（FFT）分析基波和谐波信息，进而利用电压、电流的基波及谐波信息进行电容器组参数在线辨识的方法，仿真和现场试验验证了其可行性。

1 电容器组参数在线辨识理论算法

1.1 电容器组回路等效电路模型

串联电抗器的电容器组的单相等效电路模型[5]如图1所示，图中，C为无功补偿电容器的电容值；L为串联的电抗器的电感值；R为电容器和电抗器的等效电阻。通过测量回路的电压、电流，分析基波和谐波相量，可得到各个参数。

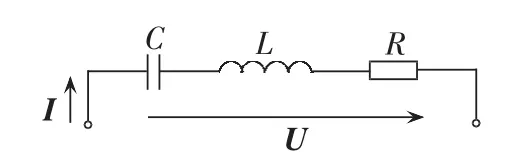
图1 电容器组回路等效电路图Fig.1 Equivalent circuit diagram of capacitor branch

1.2 电容器组参数辨识算法

测量电容器回路的电压和电流，并对其进行傅里叶变换，可以得到基波及各次谐波的电压、电流相量：U1、I1，U2、I2，…，Uh、Ih。 通过以上数据，结合图1所示电路图可列出如下方程组：

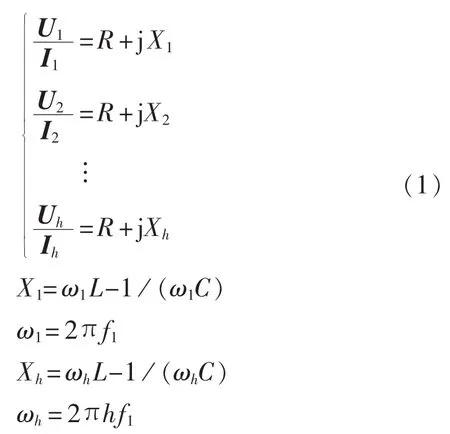
其中，X1为回路对应的基波电抗值；Xh（h=2，3，…）为回路对应的h次谐波电抗值。

对于电阻值的测量，理论上可通过其中任何一个方程按R=Re（Ui/Ii）求得电阻值，也可综合考虑基波及谐波信息进行冗余测量。但在实际测量中发现基波电压、电流测量的准确度要优于谐波电压、电流测量的准确度，因此电阻值按式（2）计算比综合利用基波和谐波信息计算有更高的测量精度。

对于电容和电感值的测量，为了表述方便，记Zi=Ui/Ii，则式（1）可写为：

R 可按式（2）计算，则式（3）变为：

理论上，在式（4）中，选择基波和任何一次谐波相量或者选择任何2次谐波相量即可求解得出L和1/C。但在实际测量中，测得的基波及谐波相量均有误差，只利用基波及某一次谐波相量信息计算所得结果的精度及稳定性受随机误差影响较大，效果较差。为了增加测量的冗余度，以便进一步提高测量结果的精度，可将测得的基波及含量较大的各次谐波相量信息均用于电容器参数的辨识。当利用基波、2次以上谐波相量信息计算参数时，式（4）为超定方程组，记：

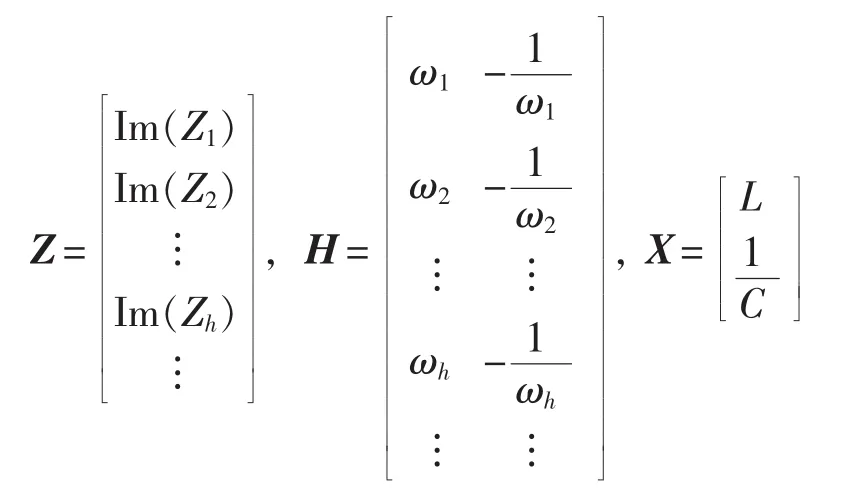
则式（4）可写为：

其最小二乘解为：

对离散采样的电压、电流数据进行分析可得基波及各次谐波的频率、幅值及相位，则Z和H均可求得，通过式（6）即可求得L和1/C值。

在上述计算过程中，准确地测量计算频率、基波及谐波相量对得到准确的电容器参数至关重要。在实际测量中，系统频率总是在一定范围内波动，由于非同步采样和数据截断时会产生频谱泄漏和栅栏效应[6-7]，影响基波和谐波分析的精度，进而影响电容器参数测量的准确度。为了减小非同步采样和数据截断带来的误差，通常采用加窗插值傅里叶变换算法[8-14]，常用的窗函数有汉明窗[8]、Blackman 窗[9]、Blackman-Harris窗[10]等，以上加窗插值FFT算法在减少谱泄漏引起的测量误差方面都取得了一定效果。为了进一步提高测量精度，本文采用8项最小旁瓣余弦窗[13]进行加窗插值FFT，测量结果精度较加经典的常用窗函数有较大提高。

2 采样数据的加窗插值FFT处理算法

2.1 窗函数的选择

为了降低频谱泄漏对测量带来的误差，应选择旁瓣峰值电平小且旁瓣渐近衰减速率大的窗函数对信号进行处理。具有良好旁瓣性能的最小旁瓣窗是一种余弦组合窗，其时域表达式为：

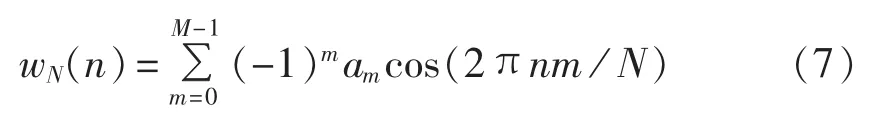
其中，M 为窗函数的项数；n=1，2，…，N-1，其中 N 为采样点数。

几种旁瓣性能较好的最小旁瓣窗函数系数如表1所示[13]，表2给出了最小旁瓣窗及其他余弦组合窗的旁瓣特性。

表1 6、7、8项最小旁瓣窗的系数Table 1 Coefficients of 6-，7-and 8-term minimum sidelobe windows

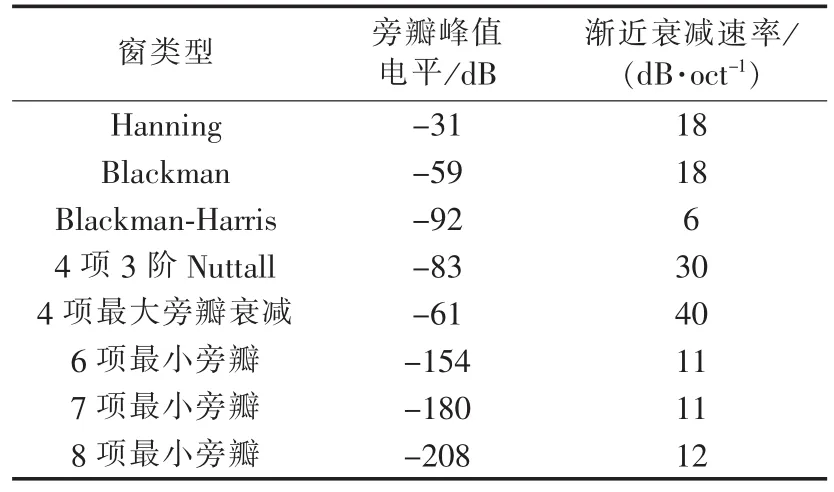
表2 余弦组合窗的旁瓣特性比较Table 2 Comparison of sidelobe characteristics among cosine composite windows

由表2可以看出8项最小旁瓣窗具有很小的旁瓣峰值，且具有很大的主瓣宽度，本文选择该窗对被分析信号进行加窗处理，可以起到很好的频谱泄漏抑制效果。

2.2 加窗插值算法

以含整数次谐波分量的信号x（t）为例进行分析，x（t）以采样频率fs均匀采样得到的离散时间信号为：

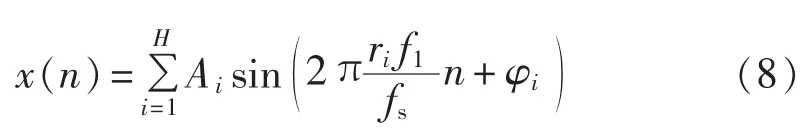
其中，H为含有谐波分量的个数；fs为采样频率；当i=1 时，ri=1，f1、A1、φ1分别为基波信号的频率、幅值和初相位；当 i≠1 时，ri、Ui、φi分别为第 i项谐波信号的次数、幅值和初相位；n=1，2，…，N为采样点编号。

对 x（n）加如式（7）所示的余弦窗函数，可得到xw（n） =x（n）wN（n），忽略负频点旁瓣的影响，xw（n）的离散傅里叶变换为：

其中，Δf=fs/N；W（k）为窗函数的离散傅里叶变换。

考虑到N≫1，式（10）可近似表示为：

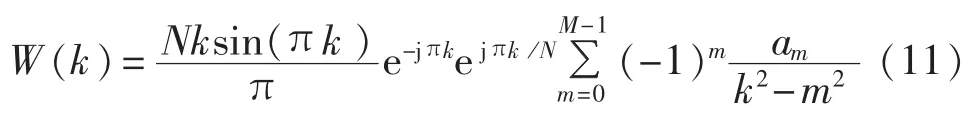
为不失一般性，设需要测量的为第i（i≤H）次谐波，为简单起见，忽略其余各次谐波对第i次谐波的泄漏影响，此时，式（9）变为：

对于第i次谐波，对信号非同步采样时，由于栅栏效应，信号的频率kiΔf很难正好位于抽样频点上，即ki=fi/Δf一般不是整数。设在峰值频点ki附近抽样得到的幅值最大谱线为ka，其左边谱线为ka-1，右边谱线为 ka+1，记 δ=ki-ka，则有-0.5＜δ＜0.5，准确地求得δ是求解问题的关键。在非同步采样情况下，加窗FFT后幅值最大谱线及其左右谱线均具有较大幅值，说明含有丰富的与实际谱线相关的信息，3根谱线的信息均可用于插值修正[15]。 记，另记：

由式（12）和式（13）可得：

当 N 较大时，式（14）一般可以简化为 α=g（δ），其反函数记为 δ=g-1（α）。 当窗函数 wN（n）为实系数时，其幅频响应 W（2πf）是偶对称的，因此函数 g（·）及其反函数 g-1（·）都是奇函数。 计算 δ=g-1（α）可采用多项式逼近方法。采用8项最小旁瓣窗函数，在MATLAB中通过仿真，用拟合函数polyfit（·）拟合可得：

求得δ后，可求得信号i次谐波频率：

信号的幅值和相位也可通过关于δ的修正函数求得。

为了更准确地求得信号的幅值，将y1、y2和y3用于幅值修正。通过对这3根谱线幅值进行加权平均计算出实际的峰值点的幅值。考虑到y2为最大谱线幅值，在加权平均时给y2以较大权重。由式（12）可得，从而有：

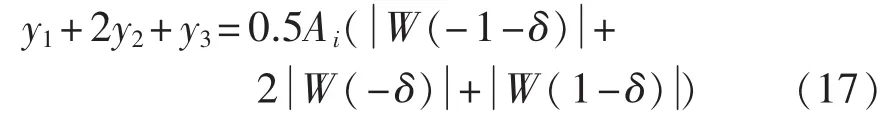
由式（17）得：

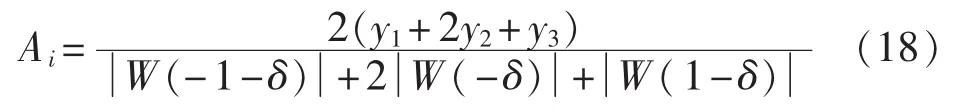
对于一般的实系数窗函数，当N较大时，式（18）可表示为 A1=N-1（y1+2y2+y3）v（δ）的形式，其中 v（·）是偶函数。采用多项式逼近求出函数v（·）的近似计算公式，结果中将不含有奇次项。采用8项最小旁瓣窗时，在MATLAB环境下通过仿真，利用拟合函数 polyfit（·）拟合可得：

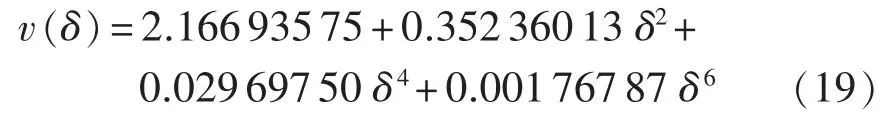
信号的相位由式（12）可得：

结合式（6），式（20）近似可表示为：

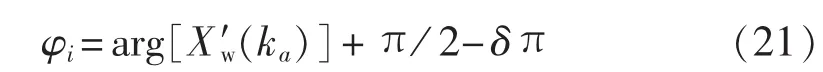
通过对输入的电压、电流信号用8项最小旁瓣窗函数进行加窗处理，进行FFT，再按式（13）—（21）插值修正公式计算基波频率f1及基波、谐波的电压、电流的幅值和相位后，即可按式（2）和式（6）计算得到电容器组回路参数R、C、L。

3 仿真试验

为了验证本文算法的可行性，在MATLAB环境下进行了仿真试验，图1所示模型中，电抗率取为较普遍的 12%，各元件取值为：C=215 μF，L=5.66 mH，R=0.05 Ω。所加电压信号表达式为：

各次电压幅值及相位如表3所示，对应的电流信号表达式为：

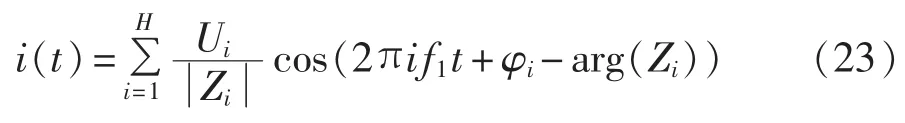
其中，Zi为回路的i次谐波阻抗。取f1=50.5 Hz，采样频率fs=12.8 kHz，采样点数N=2560。

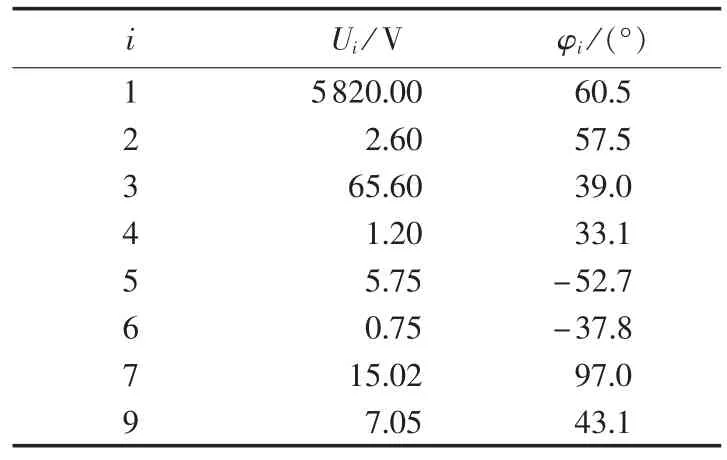
表3 仿真信号电压的基波及谐波成分Table 3 Fundamental and harmonic components of voltage simulation signal

对输入的电压、电流信号分别用Hanning窗[14]、Blackman 窗[14]、Blackman-Harris窗[12]双谱线插值FFT和本文方法进行处理，本文方法的仿真实验程序流程如图2所示，图中，fu1、fi1分别为基波电压和基波电流的频率；fuh、fih分别为第h次谐波电压和电流的频率。计算出基波频率f1及基波和各次谐波的电压、电流的幅值和相位后去除含量较低的偶次谐波信息，选择基波和含量相对较高的3、5、7、9次谐波相量信息按式（2）和式（6）计算电容器组回路参数R、C、L。仿真试验结果见表4。

图2 仿真程序流程图Fig.2 Flowchart of simulation

表4 R、L、C相对误差比较Table 4 Comparison of relative error of R，L and C

由表4数据可看出，8项最小旁瓣窗具有良好的频谱泄漏抑制作用，本文方法测量结果与加Hanning、Blackman和Blackman-Harris双谱线插值算法相比精度要高出几个数量级。

为了仿真实际测量情况，对如式（22）和式（23）信号采样的离散数据加入白噪声干扰，电压、电流信号的信噪比均为70 dB（本文测量系统所用的AD转换器性能优于70 dB），电网频率为49.50、49.75、50.00和50.25 Hz时本文方法的单次测量结果误差见表5。通过观察多次测量结果发现单次测量误差εR＜2%、εL＜1%、εC＜0.5%，通过多次测量求平均值可获得更高精度。由此可以看出本文方法能有效克服电网基波频率变动对测量结果的影响，同时在测量数据含有白噪声但信噪比足够大时也具有一定的测量精度，可用于实际测量。

表5 不同频率下测量结果的相对误差Table 5 Relative error of measurements under different frequencies

4 测量系统的硬件实现

基于本文算法，在研制的电能质量监测仪上实现电容器组参数的在线辨识功能。测量系统的硬件结构如图3所示。

图3 测量仪器硬件结构框图Fig.3 Hardware framework of measuring equipment

数据采集模块主要由电压电流互感器、信号调理电路、抗混叠滤波器和A/D转换器等电路组成。A/D转换器采用ADI公司的16位高速、6通道同步采样芯片ADS8364。装置对每通道的采样速率设定为12.8 kHz。为了适应数据的高速采样，采用双CPU结构。DSP采用TI公司的数字信号处理芯片TMS320F2812，负责ADC转换数据的读取及放入双口RAM。数据处理核心部分选择使用三星公司的S3C2440AL-40ARM芯片作为主控芯片，它拥有一个ARM9内核，稳定运行于400 MHz，负责数据的处理及通信等工作。

5 现场实际运行

在沧州地区电网某220 kV变电站进行了电容器组参数的现场实测，该变电站无功补偿电容器组装设在10 kV母线上，10 kV母线为单母线分段接线，两段母线各装设4组电容器组。

首先给出Ι段母线521号电容器组参数的测量数据。该电容器组电容铭牌参数为212 μF，串联的电抗器的电抗率为4.5%，据此可算出其电感值为2.1507 mH。采样频率为12.8 kHz，截取的数据采样点数N=2560。对采样的电压、电流信号用第2节所述方法进行加窗插值FFT分析，某次测量计算得到的基波频率f1=49.966 Hz，电压和电流的基波及含量相对较大的3、5、7和9次谐波的幅值和相位如表6所示。

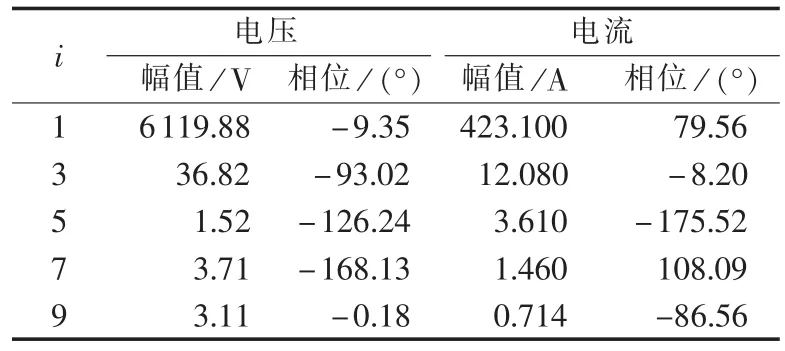
表6 被测电压、电流信号的分析结果Table 6 Results of signal analysis for measured voltage and current

利用表6数据再根据第1节所述方法进行参数计算可得：R=0.275 Ω、C=210.52 μF、L=2.131 mH，与铭牌值基本一致。

在参数实际测量时，取20次单次计算（利用2 560点的数据量进行1次计算）结果的平均值作为一次测量结果，可获得较为稳定的测量结果。Ι段母线4组电容器组A相电容值的铭牌值、停电实测值及本文方法测量结果见表7，本文方法在线实测结果与铭牌值和停电实测值较为接近，测量结果可以作为判断电容器性能的依据。

表7 电容器组电容值实测结果与铭牌值和停电测量值对比Table 7 Comparison of capacitance among online measurement，nameplate value and offline measurement for different capacitors

6 结论

本文提出了利用电压、电流基波及谐波相量进行电容器组参数在线辨识的方法，推导了加8项最小旁瓣窗函数的插值FFT算法，并将该算法应用于电容器组参数的在线辨识。仿真试验和现场实际运行验证了本文所提方法正确可行且具有较高的测量精度。设计的测量系统使用灵活方便，测量结果精确、稳定，可用于电容器组参数的在线辨识。