基于温度特征量的风电机组关键部件劣化渐变概率分析

李 辉，胡姚刚，李 洋，杨 东，欧阳海黎，兰涌森，唐显虎

（1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044；2.中船重工（重庆）海装风电设备有限公司，重庆 401122；3.重庆科凯前卫风电设备有限责任公司，重庆 401121）

0 引言

并网风电机组运行条件恶劣，其各部件受多种不确定因素的影响而发生渐变劣化直至失效，这导致风电机组频繁出现故障，特别是关键部件一旦故障，如主轴承故障、齿轮箱故障、发电机故障等，检修时间较长，严重影响发电量，且使风电场的运维和检修费用居高不下[1]。基于风电机组状态监测信息，较早掌握风电机组关键部件的劣化程度及渐变趋势，可为确定合理的检修时机提供依据，为风电场的安全经济运行提供重要的技术支撑[2-3]。

现有风电机组的状态监测手段多倾向于通过增置振动加速度传感器，来实现对风电机组关键部件的振动状态监测，然而，风电机组常在不同转速下频繁切换运行，这使得振动特征量易受到各种不确定噪声干扰影响，较难通过算法准确提出关键部件早期的劣化征兆。而反映关键部件劣化的温度特征量具有热惯性特征，抗干扰能力强，通过探索温度特征量与关键部件劣化关联关系，将不失为一种研究风电机组关键部件的劣化程度及渐变趋势的新思路。近年来，国内外学者对风电机组关键部件劣化程度及变化趋势方面的研究鲜见报道，在风电机组运行状态监测和评估研究成果略有涉及，如文献[4-8]分别基于数据采集与监视控制（SCADA）系统的温度特征量，转速、风速、电气等特征量的运行数据，利用层次分析法、模糊综合评判、物元理论和高斯混合模型对风电机组的整体状态进行了评估。文献[6-7]引入劣化度来表征部件的劣化程度，其中，文献[6]计算部件劣化度需要风电机组正常状态下的大量历史数据作为先验模型，对于新投运的机组显然不适合；文献[7]因没有考虑机组工况变化因素，以固定的预警阈值和启动允许值为依据来作为温度特征量评估指标劣化度的上、下阈值，难以准确地掌握关键部件的劣化程度和渐变趋势；文献[8]从多信息融合角度，建立了基于高斯混合模型风电机组健康状态评价模型，采用健康衰退指数作为整机健康状态评价结果，没有涉及对机组关键部件劣化趋势的研究，使得评估结果很难准确分析其状态变化过程。因此，为了掌握风电机组关键部件运行状态，特别是其故障早期的状态变化过程，有必要开展风电机组关键部件劣化渐进变化趋势的研究。

本文基于风电机组关键部件温度特征量监测数据，引入劣化度概念，提出风电机组关键部件劣化渐变趋势的概率分析方法。首先，针对采用固定阈值不能准确确定风电机组关键部件劣化度的问题，考虑机组工况变化因素，基于风电机组关键部件的温度特征量和转速信息，分别提出基于数据拟合和机群划分思路的劣化度上下限动态阈值确定方法，并对关键部件的劣化等级进行划分；其次，考虑部件劣化度会随不同运行工况而波动及随寿命递减而改变，通过非参数核密度估计方法建立部件劣化度的概率密度函数，对不同监测周期内部件劣化度的概率特征差异进行分析，获取风电机组关键部件在各监测周期的劣化等级及其劣化渐进趋势；最后，以某风电场的1.5 MW风电机组的发电机后轴承劣化渐变情况为实例，来验证本文方法的有效性。

1 基于动态阈值的风电机组关键部件劣化度

1.1 风电机组关键部件的温度特征量

传动链是风电机组的核心部件，是以旋转形式实现风能到机械能再到电能转换的必要部件[9]，其关键部件一般包括：主轴承及其支撑轴承、齿轮箱和发电机，如图1所示。

图1 风电机组关键部件Fig.1 Critical WTGS components

大多数风电场SCADA系统都对传动链关键部件的温度进行监测，如主轴承温度、齿轮箱轴承温度、齿轮箱油液温度、发电机绕组温度、发电机轴承温度等温度特征量。本文基于温度特征量运行数据，引入劣化度[7]的概念，表征风电机组关键部件良好状态与劣化状态相比的相对劣化程度。不同劣化度反映部件不同的劣化程度。温度特征量属于越小越优型指标，其计算式为：

其中，g（x）为关键部件的劣化度；x为温度特征量的监测数据；β1和β2分别为劣化度下限和上限阈值。由于风电机组运行工况的不确定性，导致合理设置劣化度的上、下限阈值是准确确定相应部件劣化程度的关键，也是掌握其渐变趋势的基础。

与关键部件温度相关联的特征量主要包括外部环境温度、风速、转速、功率等特征量。考虑现有大功率并网风电机组变速恒频运行特点，目前风电机组的运行控制大部分按照发电机转速进行风电机组功率控制，不同转速具有不同功率出力，导致关键部件可能存在不同温度量的表征。因此，考虑其温度特征量具有热惯性特征和抗干扰能力强的特点，本文在劣化度上限阈值确定问题上，利用风电机组转速与温度特征量存在较强的关联性，提取部件劣化故障前的转速和温度特征量历史运行数据，通过数据拟合的方法建立两者之间的映射，确定不同转速下部件劣化度的上限动态阈值；同时，在劣化度下限阈值确定问题上，由于运行在同一工况下的风电机组，其良好的部件运行时温度较劣化的部件温度值低，可基于机群划分思想，将风电场内转速相近机组划分到同一机群，将机群中相同温度特征量的最小温度值，作为机群内机组的部件劣化度下限动态阀值。

1.2 基于数据拟合的劣化度上限动态阈值确定

当关键部件已严重劣化时，运行在不同转速下的关键部件温度特征量幅值高于部件良好运行时的幅值。基于此，从风电机组SCADA系统中，提取关键部件严重劣化导致温度超限停机故障前的转速和温度特征量运行数据。应用bin方法[6]进行数据提取，再通过数据拟合的方法建立两者之间的映射，求得自变量为转速、因变量为温度特征量的数学函数f（n），随转速变化的f（n）即为劣化度的上限动态阈值。详述如下：应用bin方法，得到劣化严重的部件的温度特征量和转速的 q 组运行数据（x′1，n′1）、（x′2，n′2）、…、（x′q，n′q），运用数据拟合方法得到转速与温度的函数表达式为 x′=f（n′），将随转速变化的温度值作为劣化度的上限动态阈值β2，计算式如式（2）所示。

1.3 基于机群划分的劣化度下限动态阈值确定

采用风电场机群划分，将运行在同一工况下的风电机组划分为同一机群，寻求在单一机群中的各机组相同温度特征量运行数据中最小温度值，作为机群内机组的劣化度下限动态阈值。

对风电机组而言，风力机转速比风速更能准确地反映机组的运行工况[10]。风电场SCADA系统实时监测风电场内所有机组的转速变化情况，可根据风力机转速监测数据来进行机群划分，尽可能地将运行在相同工况下的机组划分到同一机群。机群的划分方法是用2个机组转速之差的最大值来反映其转速的相同程度，当这个最大值小于某个给定的门槛值ε时，则可以将它们归到同一机群里[11]。此时划分机群的依据为：

其中，ni（t）和 nj（t）分别为 i号机组和 j号机组在 t时刻的转速值；根据文献[10]，门槛值取ε＜1 r/min。

在确定以转速为机群划分的依据后，采用c均值聚类算法对风电场内所有机组进行机群划分[12]。假设风电场中共有k+m台机组，若某个时间段内有k台机组并网运行，m台机组由于某些原因而与电网脱离，则将m台离网的机组剔除，选取在该时间段内并网运行机组的转速数据作为样本，转速在该时段内的采样点数为k个。以k台机组转速｛n1，n2，…，nk｝为机群划分的依据，机群划分流程如图2所示。

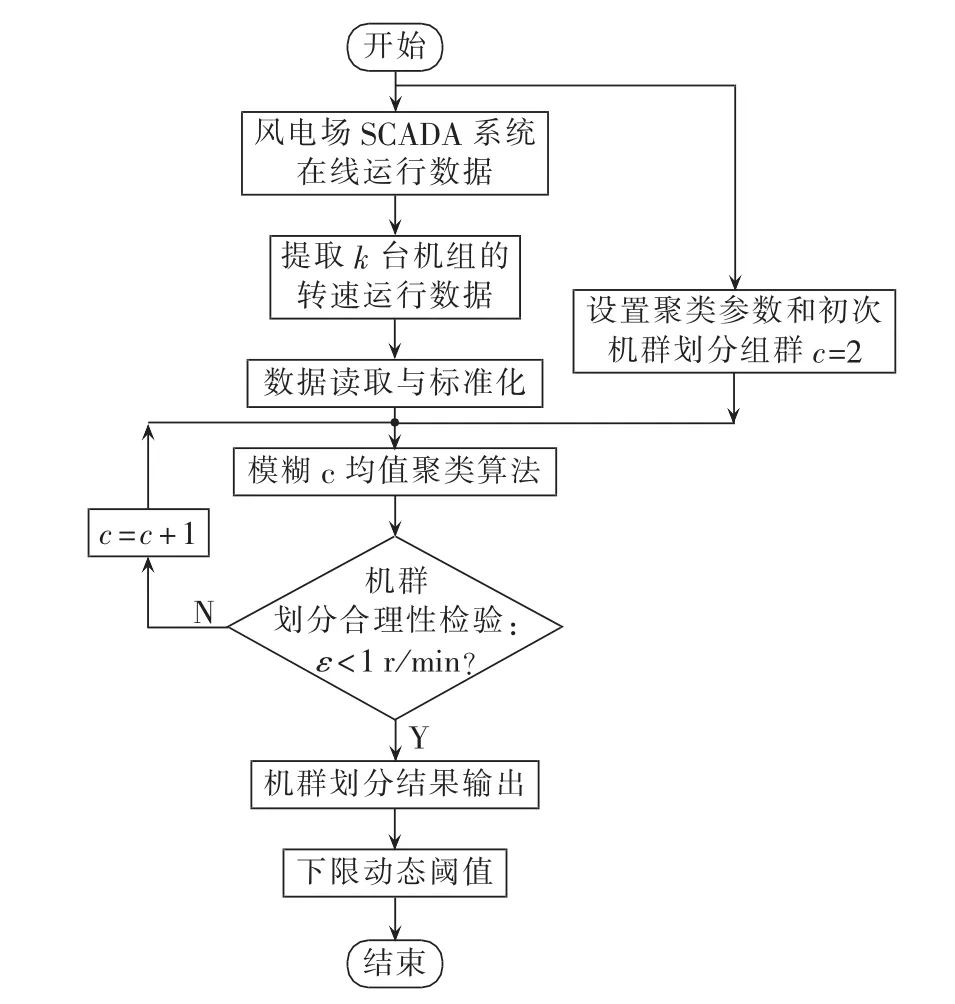
图2 机群划分流程图Fig.2 Flowchart of turbine grouping

机群划分主要包括以下3个步骤。

a.分别从风电场SCADA系统运行数据中提取k个机组转速；需设置模糊c均值聚类算法的参数包括：幂指数为3，最大迭代次数为200，初次机群划分组数c=2。

b.将k个转速运行数据进行标准化处理后输入到模糊c均值算法中，按照步骤a所设置的参数，经迭代计算得到初步的机群划分结果。

c.对步骤b中的机群划分数目进行合理性检验，若不满足ε＜1 r/min，则机群数自动加1，重新进行机群划分；否则，输出机群划分结果。

通过上述的机群划分，得到 c 个机群 D（i）（i=1，2，…，c），用 x（ij）表示机群 D（i）中 j号机组的部件的温度特征量的监测数据，机群 D（i）中 j号机组 x（ij）值越小表明部件的劣化程度越低，部件运行状态越好。基于此，β1=min（x（i））可作为机群 D（i）内机组同一部件劣化度的下限动态阈值。

1.4 关键部件的劣化度与劣化等级划分

从上述的上限和下限动态阈值的确定过程可知，部件劣化度与转速n和温度特征量的监测数据x（ij）有关，根据式（1），j号机组关键部件劣化度计算式如下：

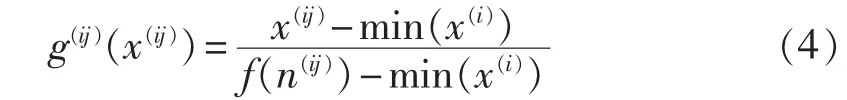
其中，f（n（ij））为劣化度的上限动态阈值；min（x（i））为劣化度的下限动态阈值；g（ij）（x（ij））为机群 D（i）中 j号机组部件的劣化度，越小越优。为更好地表征部件劣化程度，本文以文献[6-7]的风电机组评估指标的状态划分情况为依据，将关键部件劣化度分为4个等级：L=｛l1，l2，l3，l4｝=｛良好，合格，注意，严重｝，所确定的各等级所属的劣化度区间分别为l1є[0，0.30）、l2є[0.30，0.55）、l3є[0.55，0.80）、l4є[0.80，∞）。

2 风电机组关键部件劣化渐变的概率分析

2.1 基于非参数方法的概率密度函数计算

随着风电机组关键部件劣化不断加重，不同监测周期的劣化度的概率密度分布将发生一定的偏移，准确描述此偏移是研究关键部件劣化渐进变化趋势的基础。本文从概率统计角度出发，基于非参数法建立监测周期内部件劣化度的概率密度函数，并估计其置信区间，利用监测周期内概率密度函数最大值对应劣化度，结合不同监测周期部件劣化变化条件概率来表征关键部件劣化渐进变化趋势。概率密度函数的计算有参数法和非参数法，其中非参数法无需对变量的分布做任何先验假设，比参数法更符合其真实分布。因此，本文采用非参数核密度估计方法求取部件劣化度的概率密度函数[13]。

对于关键部件的劣化度周期内的时间序列g（1）、g（2）、…、g（N），劣化度 g 概率密度函数表达式为：

其中，K为核函数，本文取高斯核函数；h为宽带系数；N为监测周期内样本数量。

根据式（5）可计算得到监测周期内部件劣化度的概率密度函数。对于劣化度g，在给定显著性水平 α（0＜α＜1）下，若满足累积概率 Pc（gmin≤g≤gmax）=1- α，则称区间[gmin，gmax]为 g的双边置信区间，1-α表征了该区间包含真值的可信程度。

需指出，概率密度函数的计算与监测周期内样本数据量N有密切关系，本文采用数理统计方法确定其数值[14]。因监测周期时间长度无法与部件运行寿命相比拟，每个周期内部件相对劣化度计算过程可看作一平稳随机过程，在任意时刻相互独立，则部件相对劣化度g满足：

其中，μ为相对劣化度g均值；σ为标准差；E和D分别为期望和方差；为时间序列 g（1）、g（2）、…、g（N）总和的均值。根据切比雪夫不等式σ2/（Nλ2）可知，对于给定的置信度 1- α，只要周期内数据点数 N 满足 σ2/（Nλ2）≤α即可（其中，λ 为数据偏离均值的范围，α表示显著性水平，一般取0.05）。在参数值确定过程中，σ设置为g历史数据标准差的最大值，根据高斯分布设置λ为g历史数据标准差的3倍，本文基于大量风电机组运行数据分析表明N≥1000可满足劣化统计分析需求。

2.2 关键部件劣化渐变的概率分析

在风电机组关键部件劣化渐进变化过程中，某一部件劣化度的概率密度函数曲线由f1逐渐向f2偏移，如图3所示。图中，g1和g2分别为f1和f2最大值对应部件劣化度；δ表征f1和f2最大值的差值，δ越大，曲线f1和f2的重叠面积越小，表明部件劣化度变化越大，劣化越严重。因此，通过分析f1和f2相同区间内的累积概率以及其最大值对应部件劣化度，可实现对部件劣化变化趋势的掌握。

图3 部件劣化前后劣化度概率密度函数示意图Fig.3 Probability density function of deterioration degree before and after component deterioration

对 f1在置信度 1-α 的置信区间[gmin，gmax]，f2的累积概率Pc计算式为：

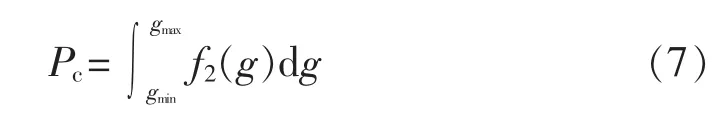
累积概率Pc与置信水平1-α反映部件劣化度的概率密度分布变化，可通过条件概率进行反映，计算表达式为：

其中，P为部件劣化变化的概率，P越大，部件劣化加重的可能性越大。

2.3 关键部件劣化渐变分析方法

为掌握部件劣化渐进变化趋势，需在单一监测周期内劣化度概率特征基础上，通过分析连续监测周期与初始监测周期内部件劣化度的概率特征差异实现。设单个监测周期内部件劣化度样本数量为N，｛g（N（w-1）+1），g（N（w-1）+2），…，g（N（w-1）+N）｝则为第w个监测周期内序列，各监测周期的概率密度函数最大值对应的劣化度gw与相对于初始监测周期的条件概率Pw的计算流程如图4所示。

在图4中，风电机组关键部件劣化度渐进变化趋势概率分析方法的具体过程如下。

a.使用非参数核密度估计方法计算第1个监测周期内部件劣化度的概率密度函数 f1（g）及 f1（g）最大值对应的劣化度g1，并估计置信度1-α对应的置信区间[gmin，gmax]。

b.计算第2个窗口内部件劣化度的概率密度函数 f2（g）及 f2（g）的最大值对应的劣化度 g2，并按式（7）求得区间[gmin，gmax]内累积概率 Pc。 根据式（8）计算第2个监测周期内部件劣化度变化的条件概率P2。P2越小，表明部件劣化变化可能性越小。

c.以第1个监测周期为基准，对后续监测周期重复上述过程，得到部件劣化变化的概率P3、P4、…、Pw，以及各监测周期概率密度函数f1（g）的最大值对应的劣化度 g3、g4、…、gw，根据这 2个序列反映部件劣化渐进变化趋势。

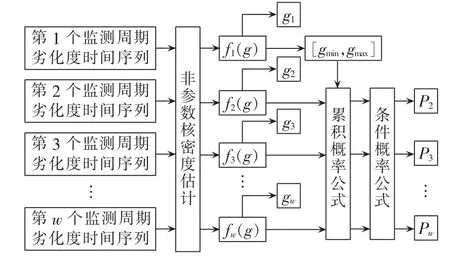
图4 风电机组关键部件劣化渐变分析流程Fig.4 Flowchart of gradual deterioration analysis of critical WTGS components

3 实例分析与验证

3.1 实例分析

为验证本文提出的风电机组关键部件劣化度的动态阈值确定及劣化渐变概率分析方法有效性，以某风电场10号风电机组的发电机后轴承劣化渐变过程为例进行验证。该机组在2012年3月29日01∶42时发生发电机后轴承故障致使机组停机，查看SCADA系统内运行数据记录，故障原因为发电机后轴承温度超过预警阈值95℃。本文以提取风电场SCADA系统内 2011年 6月 15日 10∶00至 2012年3月29日01∶42的运行数据为基础。以2012年2月11日07∶30单时刻运行数据为例，详述本文动态阈值确定及劣化度计算过程；然后，采用固定阈值与动态阈值确定方法分别对2011年 6月15日10∶00至16日15∶00运行数据进行劣化度计算，并对比这2种方法的优劣性；最后，应用风电机组关键部件劣化渐变的概率分析方法，获取在2011年6月15日10∶00至2012年3月29日01∶42期间发电机后轴承从“良好”直到“严重”各劣化等级的历经时间以及其劣化渐变趋势。

3.2 基于动态阈值的发电机后轴承劣化度计算

为了详述动态阈值的确定以及劣化度的计算过程，以2012年2月11日07∶30时运行数据为例，依据前面所述的数据拟合和机群划分方法分别确定发电机后轴承劣化度的上限和下限动态阈值后，按照式（4）计算发电机后轴承的劣化度。

a.上限动态阈值β2确定。按照1.2节所述，统计该风电场内发电机后轴承温度超限停机故障前3 d的转速和发电机后轴承温度运行数据，应用bin方法提取了转速范围为10～18 r/min的发电机后轴承温度历史运行数据。通过数值拟合方法得到了转速和发电机后轴承温度特征量之间的映射关系，上限动态阈值β2的数学函数式为：

另外，将实际值与拟合值进行比较，如图5所示，实际值围绕在拟合曲线上下波动，拟合效果较好。

图5 发电机后轴承温度上限阈值数据拟合曲线Fig.5 Data fitting curve for upper threshold of generator rear bearing temperature

a.下限动态阈值β1确定。按照图2所示的机群划分流程，除30号机组处于停机状态不参与机群划分外，其他32台机组的转速将作为机群划分的依据，通过采用c均值聚类的迭代算法，进行机群划分。机群划分结果见表1，可知，机群 3（D（3））中包括 10、19号机组在内的共18台机组，其中，19号机组的发电机后轴承温度为 43.8℃，为 D（3）内最低，即43.8℃为10号机组发电机后轴承的劣化度的下限动态阈值。

c.发电机后轴承劣化度计算。在确定劣化度动态阈值后，根据式（4），发电机后轴承劣化度为：

同理，其他监测时间的发电机后轴承劣化度均可按上述过程计算得到。

3.3 固定阈值确定方法与动态阈值确定方法对比

以2011年6月15日10∶00至16日15∶00，刚检修后的发电机后轴承采样时间间隔为1 min运行数据为例（一般认为刚检修后的部件为“良好”劣化等级[8]），采用动态阈值确定方法与文献[7]的固定阈值确定方法分别计算该时段的发电机后轴承的劣化度，对比分析如下。

该机组的发电机后轴承温度的固定上限阈值（预警阈值）和固定下限阈值（启动允许值）分别为95℃和5℃，确定的动态阈值见图6。相对于固定阈值，动态阈值的上、下限阈值随转速变化而改变，分别位于发电机后轴承温度上、下位置。采用固定阈值和动态阈值计算的发电机后轴承劣化度曲线如图7所示，可见采用固定阈值计算得到的劣化度曲线追踪转速变化趋势而明显改变，劣化度曲线在[0.25，0.48]较宽的范围内变化，无法准确确定此时发电机后轴承的劣化度；而考虑了转速变化，采用动态阈值计算得到的劣化度曲线整体波动较小，劣化度值大致在[0，0.45]范围内围绕 0.23 上下波动，因 0.23є[0，0.30），发电机后轴承劣化等级为l1，即“良好”，与实际相符。采用动态阈值确定方法，更能准确反映发电机后轴承的劣化程度。另外，通过图7中采用动态阈值确定的劣化度曲线数据获取的频率直方图如图8所示，可以看出频率直方图与高斯分布的密度函数符合较好，服从高斯分布。

表1 2012年2月11日07∶30某风电场的机群划分结果Table 1 Results of turbine grouping for a wind farm at 07∶30 on February 11，2012

图6 采样间隔为1 min时发电机后轴承劣化度分布Fig.6 Deterioration degree distribution of generator rear bearing when sampling interval is 1 min

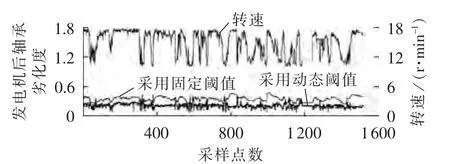
图7 采用固定阈值和动态阈值法的劣化度曲线对比Fig.7 Comparison of deterioration degree curve between fixed threshold method and dynamic threshold method

图8 频率直方图和高斯分布密度函数Fig.8 Frequency histogram and Gaussian distribution density function

3.4 发电机后轴承劣化渐变概率分析

整理 2011年6月15日10∶00至 2012年3月29日01∶42发电机后轴承从检修后到发生温度超限停机故障期间的SCADA系统运行数据，并提取机组发电运行时采样间隔为10 min的发电机后轴承温度特征量运行数据，采用动态阈值方法，计算得到各采样时间的劣化度见图9，随着发电机后轴承劣化加重，其整体趋势不断上升。当取监测周期内样本数据量为1 000、连续监测周期时间间隔为500 min时，按照2.3节的所述的关键部件劣化渐变分析方法，10号机组发电机后轴承不同监测周期概率密度函数最大值对应的劣化度以及条件概率分布见图10。结合1.4节的劣化等级划分内容及图10中结果，可从4个阶段简述发电机后轴承劣化渐变过程。

图9 采样间隔为10 min时发电机后轴承劣化度分布Fig.9 Deterioration degree distribution of generator rear bearing when sampling interval is 10 min

第1阶段：劣化等级为“良好”。监测周期数目在1～40之间，劣化度在约为0.26，劣化条件概率较小，约为0.05。其中，在监测周期40～44之间，概率密度函数最大值对应的劣化度开始由0.26上升至0.29，劣化条件概率也由0.05上升至0.22，发电机后轴承有从“良好”向“合格”劣化等级渐变趋势。

图10 发电机后轴承劣化渐变趋势概率分析结果Fig.10 Result of gradual deterioration probability analysis for generator rear bearing

第2阶段：劣化等级为“合格”。在监测周期45～175之间，两曲线虽然存在波动，但其具有整体上升的趋势。概率密度函数最大值对应的劣化度由0.30上升接近于0.55，劣化条件概率也由0.23上升至0.75，发电机后轴承有从“合格”向“注意”劣化等级渐变趋势，“合格”等级历经时间65500min，约45.5d。

第3阶段：劣化等级为“注意”。在监测周期176～231之间，两曲线仍处于整体的上升趋势。概率密度函数最大值对应的劣化度开始由0.55上升接近于0.79，劣化条件概率由0.77上升至0.99，发电机后轴承有从“注意”向“严重”等级渐变趋势，“注意”等级历经时间28000 min，约19.4 d。

第4阶段：劣化等级为“严重”。在监测周期232～357之间，两曲线仍处于整体的上升趋势。概率密度函数最大值对应的劣化度开始由0.8上升接近于0.94，劣化条件概率为0.99不变，发电机后轴承劣化已经严重劣化且不断加深，到发生温度超预警限制95℃ 故障强迫停机时，“严重”等级历经时间67000 min，约 46.5 d。

另外，应用本文方法，可在发电机后轴承发生温度超限故障的95000 min，约66 d前，较早得知发电机后轴承处于“注意”劣化等级；同时，在劣化等级转换过渡过程中，还可根据条件概率来掌握部件劣化渐变增长趋势。条件概率增长越快，表明发电机后轴承劣化概率分布差异增大，发电机后轴承劣化趋势越严重。此外，本文方法还能展现发电机后轴承在长期承受恶劣环境和交变载荷等运行环境下，经历的从量变到质变的渐变过程。

4 结语

基于风电场SCADA系统的运行数据，本文利用风电机组关键部件的温度特征量和转速信息，分别提出基于数据拟合和机群划分思路的劣化度上下限动态阈值确定方法；并应用非参数核密度估计法建立风电机组关键部件劣化度的概率密度函数，提出了基于温度特征量的风电机组关键部件劣化渐变的概率分析方法。通过实例验证，结果表明：与采用固定阈值确定方法相比，本文提出的动态阈值确定方法更能准确确定部件劣化度；利用在不同监测周期之间部件劣化度的概率特征差异，应用非参数核密度估计法，通过分析监测周期之间的概率密度函数最大值对应劣化度偏移和条件概率，可得到风电机组关键部件历经各劣化等级后直至失效的各监测周期的劣化等级以及劣化渐变趋势。