考虑响应不确定性的可中断负荷参与系统备用配置的协调优化

王蓓蓓，李义荣，李 扬，窦 迅

（1.东南大学 江苏省智能电网技术与装备重点实验室，江苏 南京 210096；2.南京工业大学 自动化与电气工程学院，江苏 南京 210009）

0 引言

智能电网与需求响应是当前电力行业的研究重点[1]，许多国家和地区已经将智能电网作为发展的重要目标，进行了广泛的研究和实践。智能电网通过优化电力基础设施的运行和管理，能够极大地促进需求响应项目的实施。同时，智能电网对电网的可靠性也提出了更高的要求[2-3]，而需求响应的实施有助于缓解系统的可靠性问题。

作为一种需求响应技术，可中断负荷（IL）就是以合约等方式允许有条件停电的负荷[4]，在系统需要时主动或受控地采用调控手段，在允许时间内削弱部分负荷，减少系统有功缺额，也就相当于向系统提供了备用容量，从而提高了系统的可靠性，提升了系统供电质量和经济效益[5-8]。随着智能电网建设的逐步展开和需求侧的逐步开放，IL作为一种虚拟的备用发电容量资源和输电容量资源，在调峰和降低阻塞等方面越来越受到关注[2，5]。文献[9]介绍了美国纽约电力市场中IL实施项目，项目允许IL作为应急资源参与到紧急需求响应计划EDRP（Emergency Demand Response Program）中，在系统运行备用不足时调用；文献[10]阐述了IL项目在世界各个电力市场中的实施情况，其中，在瑞典等地电力市场中，IL资源可以参与到多种运行备用中，并且基于自愿的原则，用户通过与ISO签订合同在需要时减少电能需求。上述实践表明，IL作为一种紧急备用容量资源，在应对小概率高风险的容量事故中有着重要的意义。

在考虑IL参与系统备用容量上，文献[2]提出了IL作为紧急需求响应措施参与备用市场的优化决策模型，IL容量是通过用户提交电价折扣率曲线参与日前竞价交易确定（电价折扣为电网公司向参与紧急需求响应的用户提供的用电优惠），但该文的电价折扣率曲线并未考虑其不确定性；文献[11]将IL视作一种可调度备用资源，用最优潮流算法研究了需求弹性对电力系统最优备用投入的影响，但需求弹性采用的是确定性模型；文献[6]针对IL和电源备用负荷效用上的差异，采用IL报价曲线，建立了两者同时参与备用市场的帕累托优化模型。上述研究均基于确定的IL模型，没有计及用户响应的不确定因素。

然而需求响应项目实施过程中，由于用户可能存在的对激励缺乏重视、通信延迟和消费行为改变等一系列原因，用户对激励或者价格信号的实际响应程度往往带有较大的不确定性[12]。因此，IL作为备用资源的实施方式，IL的响应情况关系着系统运行的可靠性指标大小。文献[12]利用服从一定概率分布的需求弹性来描述用户响应的不确定性；文献[13]描述了需求响应的不确定性，即对于确定的价格或者激励，需求并非确定的值，而是在一定范围内波动。但针对不确定性IL参与系统备用优化配置研究则未见报道。

本文构建了考虑不确定性的IL响应模型，模拟了用户集群IL响应效应；提出了基于蒙特卡洛模拟的IL与备用的协调优化模型，在美国加州的EDRP市场规则下，由优化模型确定满足系统可靠性要求的最优备用容量与不确定性IL配置关系；算例分析表明，在不同的可靠性要求下，优化模型中高可靠性高成本的发电机备用与低可靠性低成本IL备用的配置具有不同的特点，应根据系统中用户可靠性需求差别进行灵活配置。通过对IL不确定性进行研究，本文构建的模型有助于提高IL的控制精度，对协调IL与发电侧备用容量、达到兼顾系统可靠性和经济性运营均衡有着重要的意义。

1 考虑不确定性的IL响应模型

基于消费者心理学的用户响应行为研究表明[14]，在受到经济激励的条件下用户响应特性曲线存在死区、线性区和饱和区。传统模型中，采用确切值估测用户的响应度，而根据文献[13]的研究，在一定激励情况下，用户的负荷削减/转移量具有一定的随机性，并由此带来一定的不确定性，且用户受利益驱动，此随机性会随着激励水平的增加而减小。

因此，在传统模型的基础上，本文采用某一区间内的随机数描述IL用户的响应行为（在后文交易机制的设定中，参与紧急需求响应项目的IL用户根据激励大小自主削减负荷）。通过区间参数对实际响应情况进行模拟，使IL的响应模型更具实用价值、可靠性更高，也能在一定程度上减小激励决策面临的风险。

图1为IL用户i的响应特性曲线，IL用户的响应情况用削负荷率来描述，削负荷率表示用户实际削负荷量与用户削负荷潜力之比。当IL补偿水平x达到xi0（D点）时，用户开始削减负荷，但也有可能因为补偿低而不削减；当x达到xi1（C点）后，用户普遍做出响应，削负荷率大于零，且负荷削减量期望增加、波动范围缩小；当x达到ximax（M点）时，用户负荷削减量期望达到最大且波动范围近似忽略，所有响应潜力均已挖掘。表1描述了D、C、M点的物理含义。

根据图1的曲线，建立IL用户的响应模型。采用线性模型表达图1中用户响应行为，在某一经济激励水平x下，用户i的削负荷率λi的上、下界可分别表示为式（1）和式（2）。

图1 计及不确定性的可中断负荷用户响应特性曲线Fig.1 Characteristic curve of interruptible load with response uncertainty

表1 不确定性需求响应机理模型概念表述Table1 Conceptional description of uncertain demand response mechanism model

在某个补偿标准x下，用户的削负荷率λi波动范围是[λi2（x），λi1（x）]（如图1 中所示），通过实际数据的统计分析可近似描述其分布规律。为了简化问题，本文用均匀分布来描述某一激励水平下用户响应不确定行为。即有：

其中，U为均匀分布。

不同类型的用户，对应于图1中xi0、xi1和ximax各不相同。对于n个用户，总体的削负荷率λ（x）可表示为：

其中，PRi为用户i的IL容量。

2 考虑不确定性的IL参与系统备用协调优化模型

本文的模型着力于解决这样的备用优化问题：调度人员在日前调度计划制定时需要考虑第二天备用的安排，有2个来源：一个是发电机组提供的备用容量，一个是IL提供的紧急备用资源。一般而言在系统低谷时段发电机备用充足，而在系统高峰时段前者提供的备用往往代价较高（主要是由新建备用机组、备用机组空置率带来的），但具有较高的响应可靠性，后者由IL提供，由于响应不确定性的原因，可靠性较差，但在电网中分布广泛，运行方式灵活且成本低，具有一定的经济性；考虑系统备用安排，在购买发电机备用与购买需求侧IL容量之间存在经济上以及可靠性需求上的协调空间[15]，通过优化配置系统备用容量与IL，从而实现系统可靠性与经济性的协调。

2.1 市场模式与规则设定

在智能电网中，双向实时的通信系统的建立保证了用户积极参与电力系统运行和管理，能够实时通知用户电力消费的成本与电网的状况以及计划停电等信息。在这方面，世界各国已经有了许多成功的实践，如美国加州的EDRP，当系统运行备用紧缺或者出现严重事故时，IL收到通知后减少用电量，按照实际用量和用户的基线负荷对比确定减少量，削减时间按最少2 h计算，并据此得到补偿[9-10，16]。

本文在EDRP的市场实施模式下，研究考虑不确定性的IL参与系统备用辅助服务提供的优化协调控制。参与到EDRP的用户，当ISO或者电力公司出现运行备用短缺或者事故时，通过自愿削减负荷达到提高系统应对备用容量短缺事故的能力，并得到补偿。根据IL响应不确定性模型，不同类型用户在同样补偿标准下其响应量以及波动程度均呈现不同特性，这样就可以实施更为灵活的IL补偿方案，根据具体需求制定补偿标准，满足特定情况下的备用需求，从而达到灵活调控的目的。

本文的优化模型为满足一定的可靠度要求，通过动态调整IL合同的补偿价格主动调动需求侧资源，协调高可靠性机组备用容量与低可靠性用户IL的配置，降低系统满足可靠性要求的成本，从而提供一种更具经济性和更有效率的系统辅助服务获取机制，实现满足系统可靠性要求的机组备用容量以及IL的最优经济配置。

2.2 IL容量的确定

参与EDRP的IL用户，通过自主削减负荷进行响应，作为低补偿的IL资源，除了考虑其响应不确定性外，其负荷削减上限也需要加以确定。由于用户供电可靠性要求与其负荷削减潜力之间存在着负相关关系，和文献[17]类似，本文假定用户可以提供的最大IL容量和其综合供电可靠性需求rRELj0存在着式（5）的关系。式（5）描述了一定补偿水平下，用户j产生的削负荷量（即提供的切负荷备用容量）。

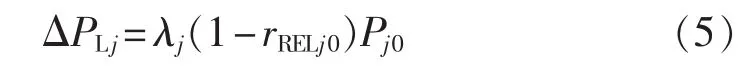
其中，λj为用户j削负荷率，是IL补偿水平的函数；rRELj0为用户j所要求的综合供电可靠性水平；Pj0为正常运行情况下用户j的有功负荷。

式（5）中，（1-rRELj0）Pj0即为用户 j的负荷削减上限。其含义为，如果用户的可靠性要求是90%，则可等效认为其100%需保证供电的负荷为rRELj0Pj0，（1-rRELj0）Pj0即为其可以提供的削负荷潜力。文献[17]即是基于此思想提出了基于需求侧可靠性差别定价的辅助服务提供新方式。

2.3 目标函数

决策模型中，待优化的变量为发电机组备用容量与IL补偿价格，目标函数为电力公司购买备用和偿付用户补偿费用的总成本最小。总成本由三部分组成：购买发电机组备用容量费、备用电量费、IL补偿。其中，备用电量费与IL补偿期望值，是通过对系统进行N-1安全校验[18]、根据事故电量缺额以及发生概率计算得到。

目标函数如下：

其中，PR为发电机组提供的总备用容量；ρR为备用容量电价；ρe为备用电量电价；Q（PR）为备用实际被调用的电量，通过进行N-1校验确定，并考虑负荷波动；x 为 IL 补偿价格；QIL（x）为 IL 削减电量；ρIL为 IL补偿价格。

PR由各发电机提供，由于本模型并未考虑发电机调度问题，因此PR是作为节点注入量进行计算。发电机组备用电量Q（PR）以及IL削减电量 QIL（x）的计算公式如下：

其中，K为发电机台数；ηk为第k台发电机组强迫停运率；Pek为第k台发电机组停运时发电侧投入的备用容量；L为线路条数；μl为第l条线路断线故障率；Pel为第l条线路故障时发电侧投入的备用容量；M为备用容量PR的分段数；L（PRm）为发电计划按照负荷预测值安排且发电备用容量为PRm时，负荷不继续增加的概率；ΔPRm为备用容量PR第m个分段的容量；表示由于负荷波动造成的备用调用量[17]；P为负荷实际值与预测值的偏差，其概率分布属于正态分布；δ为P的标准差[17]；Z为IL用户个数；ΔPLj为第j个用户的削负荷量，在进行安全校验时，将用户的削负荷量作为虚拟发电机容量注入各节点，E（ΔPLj）为削负荷量的期望值，由于用户削负荷量在一定范围内波动，并服从均匀分布，因此，在计算IL的补偿成本时，使用削负荷期望E（ΔPLj）来计算IL的可中断容量。故障持续时间、负荷波动时间以及中断时间均按照最低限度1 h计。

2.4 约束条件

（1）节点供电可靠性要求。

节点供电可靠性要求可以利用文献[17]所述的综合供电可靠性指标描述，但由于本文考虑了IL的不确定性，该指标难以计算，因此选用蒙特卡洛模拟方法来考虑[19-20]。蒙特卡洛模拟法中，首先要对系统各个元件的状态抽样，抽样的次数为样本总数，其中系统元件包括发电机、线路、变压器等，随后，在上述状态下进行交流潮流计算，统计失负荷次数。每种系统状态都对应一个试验结果。那么，电网可靠性指标可用式（11）的统一公式表示[21-22]：

其中，NS为样本总数；xi为系统状态；F（xi）为可靠性测试函数，为状态xi的一次试验结果。

本文取 F（xi）为：

在本文模型的求解过程中，对生成的每个解向量（备用容量和补偿价格）进行蒙特卡洛模拟，判断在当前解的条件下，系统的备用是否能够满足负荷需求，如果能够满足，则F（xi）的值为0；如果不能满足，系统将失去部分负荷，则F（xi）的值为1。因此，即失负荷概率 LOLP（Loss Of Load Probability）指标。

各节点供电可靠性需要满足：

（2）系统潮流约束：

其中，iєSB；PGi为节点 i处发电机提供的有功功率；Pi为节点i处的负荷；Mi为节点i处用户的数量；ΔPLij为节点i处第j个用户的削负荷量；Ui为节点i处电压；Ul为节点 l处电压；θil为节点 i、l之间电压相角差；Gil为节点 i、l之间的互电导；Bil为节点 i、l之间的互电纳；QGi为节点i处发电机提供的无功功率；Qi为节点i处的无功负荷。

（3）发电机组出力上下限约束：

其中，SG为发电机组集合。

（4）节点电压约束：

（5）线路约束：

2.5 模型求解

模型最优解的求取通过粒子群算法寻优得到。其中，对于本文模型中的约束式（13），采用蒙特卡洛模拟方法进行求解，且考虑了交流潮流约束，本优化问题为非凸优化问题，其求解利用局部粒子群算法[23-24]来实现，可避免陷入局部最优解。

2.5.1 粒子群算法流程

粒子群算法流程如图2所示。

图2 粒子群算法流程Fig.2 Flowchart of PSO algorithm

图2所示流程中，初始条件包括需要提前知道各类用户的响应曲线，并设定当前的可靠性要求、初始IL电价、初始备用容量购买量等。

算法流程的核心部分在于粒子群适应度的计算，粒子适应度为模型的目标函数（式（6））值。计算各粒子适应度时，首先判断该粒子的备用容量与IL补偿价格是否能够满足系统可靠性要求，这一步通过蒙特卡洛模拟法确定，最后再计算相应的适应度函数值，具体过程如下文所示。

2.5.2 粒子群算法适应度计算

粒子群适应度的计算流程如图3所示。可靠性约束式（13）的处理是粒子群算法适应度函数的一部分。首先利用蒙特卡洛模拟方法模拟系统的状态，通过潮流计算对预想事故状态下系统的可靠性进行判断[25]。如果可靠性指标Fn满足可靠性要求，则通过安全校验可以确定电力公司购买备用及IL补偿的总成本，即适应度函数值；如果不满足可靠性要求，此时在粒子群算法中该粒子需要被淘汰，因此设置电力公司购买备用和IL补偿总成本为最大值（该最大值为不计及IL时系统购买备用的成本），从而确定当前粒子的适应度，以适应粒子群算法的需要。

3 算例分析

3.1 算例设置

本文采用IEEE-RBT 6节点系统进行可靠性分析，母线1为平衡节点。为分析用户响应不确定性的影响，在每个节点设置100户用户，各用户用电负荷按照一定梯度分布（即下文所述5种用户类型）。备用容量电价ρR=100元/MW；备用电量价格采取合同价，为 ρe=360 元/（MW·h）[17]。

图3 粒子群算法适应度函数计算流程Fig.3 Flowchart of fitness function calculation of PSO algorithm

为了便于进行不同可靠性要求情况下的比较，将所有节点的用户可靠性要求设为同一值，即后文可靠性水平。节点每个用户的响应情况均满足图1描述的曲线。各用户根据可靠性要求及自身负荷容量，由式（5）计算其切负荷备用容量。其中，设置5类用户，每类用户临界激励与饱和激励都不相同，如表2所示。阈值的设定以国内IL项目的补偿标准为参照[5]。其中类型1、2代表中断成本较低、用电方式灵活，因此响应积极的用户（如水泥、建材、机械制造行业用户）；类型3代表中断成本相对较大，但有一定潜力空间，因此有一定响应积极性的用户（如钢铁行业等）；类型4、5代表用电单位产值较高、用电方式不灵活，因此响应积极性较低的用户（如医药、电子、轻工业等）。

表2 用户响应特性参数表Table 2 Characteristic parameters of user response

3.2 结果分析

3.2.1 集群用户响应特性分析

根据式（5），以节点可靠性水平为95%为例，在IL 补偿价格范围内（以 1000元 /（MW·h）为上限），对用户响应状态进行蒙特卡洛模拟，抽样次数N=4000得到图4所示的用户削负荷量的范围。由图可见，由于响应不确定性的存在，削负荷量随着IL补偿价格增加呈现局部波动的特性，且存在相差明显的上界和下界。由于负荷的集群效应，削负荷量整体上呈现平缓上升、光滑曲线的趋势。随着补偿价格升高，IL响应量增加速度逐渐增大，补偿价格升高到一定程度，IL响应量增速开始减少并趋于平缓，并达到饱和值。

图4 用户削负荷量集群效应Fig.4 Crowding effect of user load shedding

图5中给出了削负荷量的变化范围（图4中曲线的上界减下界）随IL补偿价格的变化情况。由图中可见，削负荷量的波动性随着IL补偿价格的增加呈现先增后减的趋势。原因在于，IL补偿价格较小时，用户响应意愿普遍较小，因而不确定性较小；IL补偿价格增大到一定程度，由于不同用户的断电成本不同，有些用户此时响应意愿较大，而有些用户响应意愿较小，因而不确定性较大；当IL补偿价格足够高时，用户普遍削负荷意愿强烈，不确定性逐渐减少。

图5 不确定性变化情况Fig.5 Variation of uncertainty

3.2.2 不同可靠性要求对备用配置情况的影响

取粒子群规模N=50，迭代次数上限T=25，蒙特卡洛抽样次数10000次。设置如下情景：各节点用户均要求93%以上、95%以上、97%以上供电可靠性。对上述情景进行求解，计算结果如表3所示，表中IL波动性量表示图4中的IL备用容量上界和下界之差；IL期望容量表示该补偿价格下IL调用的平均水平；备用总容量表示IL期望容量和发电机备用容量之和。

表3 最优备用容量与可中断负荷补偿价格Table 3 Optimal reserve capacity and compensation price of interruptible load

由表3可见，随着可靠性要求增高，购买的发电机备用容量逐渐增大，但IL期望容量则逐渐减少，供电公司付出的辅助服务购买总成本也增加。其原因在于IL相对于发电机备用而言，属于可靠性低购买成本也低的资源，随着用户要求可靠性的增加，系统需要付出更多的成本去购买高可靠性但成本更高的发电机备用资源来满足要求。

但观察表3同时也发现，随着可靠性要求的增加，IL补偿价格则是先降低然后增加，随之带来购买的IL波动量则是先增加再降低（表3的第3列），此外，表3中95%和93%可靠性需求下备用容量总容量（表3第6列）相差并不大，下文的图6和图7重点说明了这种现象产生的原因。

图6给出了不同可靠性要求下IL调用情况，通过图6可知，不同的可靠性要求下，模型确定的最优补偿价格有明显差异。对比93%可靠性要求和97%可靠性要求下的结果可知，在可靠性要求高时，由于大部分IL响应资源具有不确定性而不满足系统可靠性要求，因此优化模型必须配置更高的发电机备用容量和较少的可中断备用资源，但这些可中断备用资源的单位补偿价格必须要很高以保证其响应的可靠性；而可靠性要求较低时，从经济性角度考虑，不需要花更高的成本购买发电机备用容量，用户的IL响应资源即可以满足要求，因此如图6中所示，当可靠性要求为93%时，系统中配备的IL备用容量达到12.01 MW（期望值）。

图6 不同可靠性下可中断负荷调用情况Fig.6 Interruptible load dispatch for different reliabilities

相比于93%可靠性要求下的结果，95%可靠性要求下IL补偿价格有所降低，这是因为95%可靠性下，发电机备用容量的增加满足了可靠性的增加，此时IL补偿价格稍微减少更能满足优化结果的经济性。图7给出了3种可靠性要求下IL容量的占比情况，从图7中来看，IL备用在备用容量总和中的占比是随着可靠性要求的增加而逐渐降低的，即在可靠性要求很高的情况下（如97%），IL的占比最小，电力公司主要依靠发电机备用满足可靠性要求，原因在于高可靠性要求的IL需要通过很高的IL补偿价格来得到，这个价格相较于发电机备用价格而言不具有竞争力；而在可靠性需求降低的情况下（如95%、93%等），电力公司可依据具体的可靠性需求，通过降低发电机备用购买量和降低IL激励水平2种方式来实现，本文的模型有助于他们选择一种经济性较好的方式。从图6和图7中来看，相较于可靠性需求最低的情况（93%），95%可靠性的方式降低IL激励水平最多但发电机备用减少得不多，而93%可靠性的方式则是发电机备用减少得很多，IL激励水平降低得不大，因此造成了表3中的备用总容量在93%可靠性要求和95%可靠性要求时基本差别不大。

图7 不同可靠性下可中断负荷备用占比Fig.7 Ratio of interruptible load to system reserve for different reliabilities

将图5中所示削负荷量波动范围除以最大可削减的负荷容量之后得到波动量百分比，如图8所示，并在图中标明了不同可靠性要求下优化模型确定的IL补偿价格所对应的波动量百分比。如图所示，并对照表3，当可靠性要求为95%时，IL波动量百分比为3.60%，与可靠性要求为93%的波动量百分比相比差别不大；而可靠性要求为97%时，IL波动量百分比仅为0.32%；显然，在可靠性要求较高时，优化模型确定的IL波动量百分比大幅度降低了。这表明，在可靠性要求低时，电力公司能够容忍不确定性较大的IL，因而倾向于选择较低的补偿价格，考虑了经济性；在可靠性要求高时，电力公司只能接受不确定性较小的IL，因而倾向于选择较高的补偿价格，照顾到可靠性，本文提出的优化模型可以实现不同供电需求下的经济性和可靠性的统一。

图8 优化结果与不确定性Fig.8 Optimization results and uncertainty

4 结论

本文建立了考虑不确定性的IL响应模型，在基于EDRP的市场规则下，提出基于蒙特卡洛模拟和粒子群算法的IL与备用的协调优化模型，以确定满足可靠性要求的发电机组备用容量与IL的最优配置，并用算例分析了不同的可靠性要求下用户响应不确定对系统发电机组备用与IL配置的影响，分析得出下列结论。

a.本文建立的IL的响应模型有如下特点：单个用户的响应总量和响应的波动性随着激励水平的变化而变化，而且相对于单个用户，大量用户的集群效应造成了用户整体的削负荷总量波动性有所降低，并呈现光滑曲线的形式。

b.通过协调优化备用与IL资源，电力公司能够达到一定程度上的系统可靠性和经济性运营均衡。

c.由于用户响应不确定的普遍存在，IL在参与系统备用中有了新的特性。上述优化结果显示，不同的可靠性下备用与IL的配置情况存在着差异性。在可靠性要求低的情况下，电力公司倾向于多用IL、减少购买备用；在可靠性要求较高的情况下，电力公司倾向于更多地购买可靠性高的发电机备用。在这样一种方式下，电力公司可以根据当前系统的可靠性需求确定备用容量以及IL补偿价格，灵活配置发电机备用与IL，实现资源高效配置。