空间曲梁单边悬索桥的振动舒适性评估及减振设计*

孙利民 杨伟 于军峰 于 超

1.同济大学土木工程防灾国家重点实验室 上海 200092；2.上海现代建筑设计（集团）有限公司 上海 200041；3.上海申迪（集团）有限公司 上海 200041

以上海国际旅游度假区空间曲梁单边悬索桥西桥为例，介绍了人致振动舒适性评估过程，并根据评估结果进行了基于调频质量阻尼器（TMD）的减振设计。

1 人行桥人致振动舒适度评估理论

1.1 人行荷载的力学模型

人行激励振动的特性取决于人行荷载的特殊性。人的行走由连续的步子形成，具有周期性。这种周期性激励在竖向和侧向都可以用傅立叶级数的形式表示，级数中高阶频率是基频的整数倍，但基频的大小在竖向和侧向不同。竖向振动由人行走时重心的上下起伏对桥面产生的垂直方向上的动力荷载引起。单人行走时，基于步行力的周期性，竖向力和侧向力可用傅立叶级数的形式表示。

根据现有的研究结论，各阶谐波的动载因子取值不同，其中竖向力一阶谐波动载因子最大，高阶谐波动载因子迅速减小，一般只需考虑前三阶或四阶谐波。如Kajikawa较早建立了αν,1（竖向、侧向动载因子）随步频变化的规律；Rainer[1]等对步行、跑步及跳跃产生的竖向力随步频变化的关系进行了系统的试验研究，得出各阶谐波的动载因子随步频变化的规律。步行竖向力αν1和αν2随步频变化较显著，αν1在2.4Hz时达到最大；而αν3和αν4随步频变化不明显；Allen[2]根据Rainer的研究成果，在一般步频范围内对动载因子偏安全取值；Kerr[3]对40个人的步频介于1～3 Hz的步行力数据进行分析，表明αν1随步频增大，但高阶谐波动载因子的变化非常离散；Ellis[4]在研究大跨度轻质楼板的人致振动问题过程中，从试验楼板的振动位移和加速度响应得出人行激励，对通常步频范围内（1.7～2.4 Hz）的各阶谐波动载因子作了更仔细的研究，其中αν1与步频的关系和Rainer的结果比较接近。

德国人行桥设计指南[5]规定，计算人行荷载时，竖向动载因子αν可取0.40，横向动载因子可取0.05，取行人的标准体重G为700 N，则ανG及αlG分别可取280 N和35 N。另外，考虑到行人步频接近人行桥振动频率变化范围临界值的概率，须对人行荷载引入折减系数ψ，最终指南中对步频为fp的人行荷载定义为：

折减系数ψ按照步频的不同取值有所不同，ψ取值如图1所示。

当人群在桥上行走时，人步行对桥面产生周期性的作用力，一般情况下只引起较小的振动响应，但当步行侧向力的频率接近人行桥侧振固有频率时，将引起桥面明显的可感振动，人与桥之间开始发生强烈的相互作用过程。

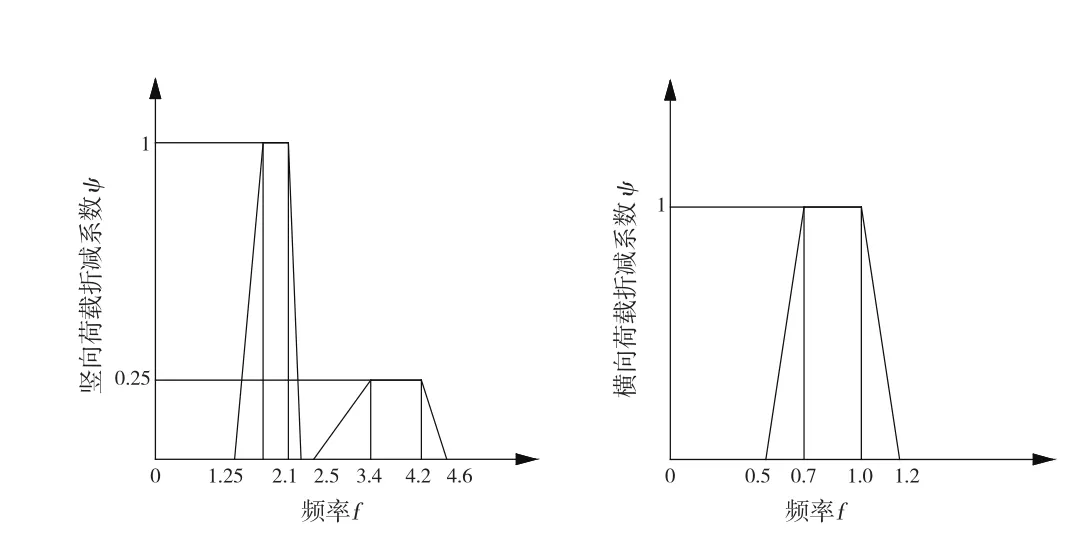
图1 人行荷载折减系数ψ

桥梁发生侧向振动会引起人群中一定比例的行人步行与振动同步，产生更大的共振荷载。行人步行发生同步与振动频率有关，仅当振动频率接近行人的侧向晃动频率时，行人才有可能调整步伐与振动同步，统计发现人行桥发生的大幅度侧向振动的频率都在1.3 Hz以内。同时，步行同步的发生还与振动强度有关，只有当振动达到影响行人的步行舒适性的程度时，行人才会相应调整步伐，可见存在一个引发同步调步行的所谓最小振幅，小于该振幅时，行人为完全随机步行。

德国人行桥设计指南指出，人群荷载等效行人数Ne与桥上人流的密集程度有关。当人群密度很小时，人群相当于自由行走。然而在高密度人流情况下时，行人行走阻塞，人流向前移动速度减缓而同步调概率增大，此时的等效行人数量的计算方法将与小密度人群时不一样。设计指南中规定计算公式如式（2）所示：

式中：d——人群密度，人/m2；

ξ——结构的阻尼比；

S——桥面人行面积。

因此步频为fp的单位面积有效人群荷载可表示为：

1.2 人行桥舒适性评价指标

人行激励振动带来的是桥梁的适用性问题，舒适性指标是未引起行人感觉不适的加速度允许值。参考国内外的一些规范中的描述，如英国规范BSI，其竖向加速度的允许值可表示为由于行人对侧向振动更敏感，侧向加速度的允许值也相对更为严格，允许值表示为其中，f为结构振动的频率。

2 人行桥人致振动分析

2.1 人行桥桥梁概况

上海国际旅游度假区空间曲梁单边悬索桥西桥桥梁结构体系主要由内、外侧主梁及空间主缆、吊索、背索和索塔组成。内、外侧主梁组成桥面系，两端固结于桥台，跨中由悬挂于主缆上的柔性吊索提供竖直向弹性支撑。主缆为空间悬链线布置，位于外侧主梁外侧；每个索塔顶部布置1根背索，背索与主跨、边跨主缆一起，保证成桥时索塔顶部的整体平衡。桥梁的总体布置如图2所示。

2.2 人行桥自振特性分析

人行桥人致振动与结构的频率相关，只有靠近人行荷载步频的结构模态才可能会被激起共振，所以需要分析桥梁结构的动力特性。图3所示为对该桥建立的全桥有限元模型。考虑结构二期恒载的影响，得到人行桥的频率、振型如表1及图4所示。

图2 人行桥（西桥）总体布置

图3 全桥有限元模型

表1 成桥状态下频率与振型

图4 人行桥各阶振型示意

2.3 人行振动舒适性评估

根据动力特性分析的结果，对该人行桥频率落入与人行激励频率较接近的范围内的振型可按单自由度振动系统简化分析[6]。振型坐标表示的单自由度运动方程如式（4）所示：

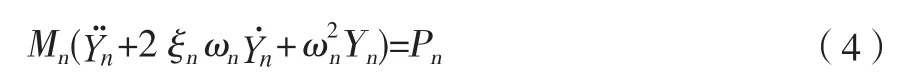
式中：Yn——第n阶振型的广义振型坐标；

Mn——振型质量；

Pn——步行振型力。

人行桥人致竖向振动和侧向振动都可采用振型分解后按单自由度系统分析，且一般情况下竖向振动和侧向振动对应不同的振型，因此可分别单独考虑。对该桥动力特性的分析表明，该桥侧向刚度较大，侧向振动的基频已超出5 Hz，已超过侧向人行荷载频率范围，因此，本文针对该桥人致振动评估将不涉及侧向振动。

在一般的情况下，人群激励荷载可以取2种工况，一种是正常使用荷载，按照我国《城市人行天桥与人行地道技术规范》相关规定，天桥与地道的设计通行能力应满足2 400 人/（h·m），若取行人平均步速为1.50 m/s，则该桥在满足设计通行能力的正常使用情况下，人群荷载的人群密度可取为0.444人/m2；另外一种工况是最不利荷载，参考国外的相关研究成果，当人群密度超过1.50人/m2时，行人行走是不可能的，其动力作用将显著地减小，因此，在计算最不利人群荷载时，可取人群密度为1.50人/m2。计算得到人群随机荷载作用下的各阶振型加速度响应如表2所示。

由表2可见，该桥在2种工况人群谐波荷载作用下所产生的最大共振加速度均超过了规范规定的振动加速度限值。当人群密度为0.444人/m2时，竖向振动加速度最大值达到0.8118 m/s2；当人群密度增大至1.50人/m2时，人群共振荷载所产生的最大竖向加速度达到3.4975 m/s2。因此，该桥在正常使用人行荷载作用以及最不利人行荷载作用下，可能会发生桥面振动过大，行人通行舒适性不佳的情况，所以有必要在设计阶段预备减振措施。

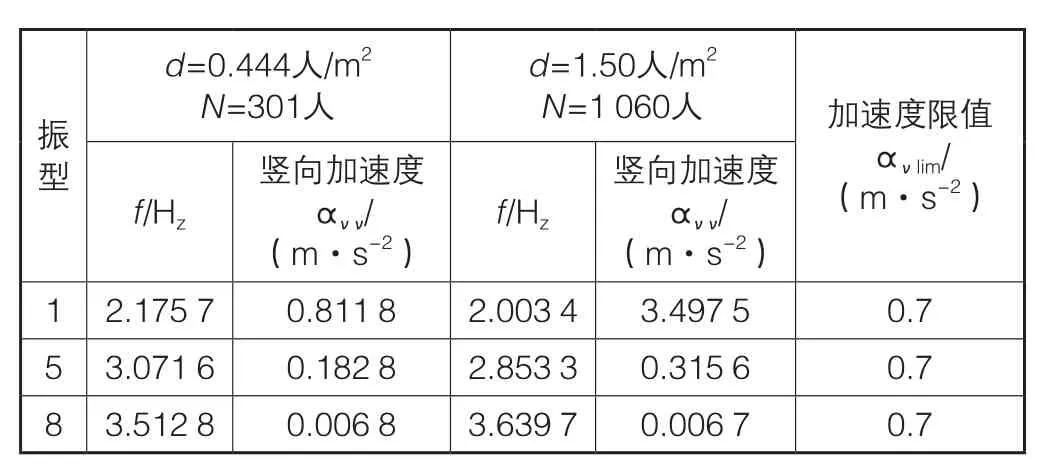
表2 单自由度系统最大加速度响应（ξ=0.01）

3 TMD减振设计

3.1 TMD设计理论基础

TMD（Tuned Mass Damper）系统就是安装在主结构上的调频质量阻尼器，属于结构被动减振控制体系的一类。如图5所示，它由固体质量块、弹簧减振器和阻尼器组成。通过改变TMD的质量或者刚度来调整其自振频率，使其尽量接近主结构的激振频率，当主结构受到激励而振动时，TMD就会产生一个与结构振动方向相反的惯性力作用在结构上，使主结构的振动反应衰减并受到控制[7]。

图5 TMD结构示意

对于图5所示的在作用力P(t)作用下的单自由度结构体，其运动方程如式（5）、式（6）所示：

式中：m、c、k——分别为主结构的质量、阻尼以及刚度；

md、cd、kd——分别为TMD的质量、阻尼以及刚度；

P(t)——外部激励荷载。

当P(t)为谐波荷载，以主结构最小加速度为优化准则，TMD的频率比和阻尼比优化值如式（7）、式（8）所示：

式中：μ——TMD质量与主结构质量比；

ξs——主结构阻尼比；

γopt——TMD优化频率比（TMD频率/主结构频率）；

ξopt——TMD优化阻尼比。

如果在主结构上安装TMD，则对于如公式（4）所示由振型坐标表示的单自由度运动方程将会变为公式（9）：

式中：Pc(t)和Pk(t)——分别为TMD对主结构产生的阻尼力和弹簧力。

假设TMD安装位置为结构i点，i点对应的振型向量值为φni，则TMD运动方程如公式（10）所示：

因此，TMD对主结构产生的阻尼力和弹簧力公式分别为式（11）、（12）：

若假设Cd=2Mdξdωd，Kd=Mdω2d，Xd(t)=则公式（13）及（14）变为公式（15）、（16）：

当P(t)为谐波荷载，以主结构最小加速度为优化准则，TMD的频率ωopt和阻尼比ξopt优化值公式如式（17）、（18）所示：

式中：μ=Md/Mn。

3.2 TMD参数设计

以最不利人行荷载作用下的桥梁振动舒适性为控制目标，该桥第1阶振型频率ωn=12.587 6 rad/s，振型阻尼比ξn=0.01，因为结构动力特性分析对振型按质量归一化处理，即Mn=1。取TMD与主结构振型质量比μ=0.029 5，可以算得，TMD的最优频率ωopt=12.422 7 rad/s，最优阻尼比ξopt=0.105 9。最终设计将TMD安装于主梁跨中，其质量块的质量为3 958.2 kg，弹簧刚度为6.108 4×105N/m，阻尼系数为1.041 8×104N·s/m，跨中截面的TMD安装示意如图6所示。

图6 主桥跨中截面TMD安装示意

3.3 TMD减振效果仿真

借助MATLAB中的Simulink软件来模拟TMD减振系统，以获取由公式（15）和（16）组成的常系数非线性微分方程组的数值解。当该桥人行桥面最大竖向及侧向加速度出现在人群共振荷载频率为2.003 4 Hz时，取主结构的阻尼比ξ=0.01，人群密度为1.50人/m2，对未安装以及安装了TMD系统的桥梁施加相同的人群共振荷载，由Simulink模拟出的人行桥面竖向最大加速度时程如图7所示。

图7 人行桥面竖向最大加速度时程

由图7可知，该桥安装TMD减振系统之后，人行桥面竖向最大加速度由原来的3.49 m/s2减小到0.44 m/s2，减振效率达到80%，减振效果明显。

4 结语

本文通过考虑人桥相互作用的人行荷载模型，综合国内外有关人行桥设计规范的规定，阐述了上海国际旅游度假区空间曲梁单边悬索桥西桥人致振动的舒适性评估过程，并结合实际情况进行了TMD参数设计。结果表明，该人行桥在人群密集的情况下，可能会发生过大的人致振动，在安装TMD的情况下，可以保证人行桥在正常运营过程中的使用性和舒适性。