基于不同优化准则的风电功率预测

张 露，卢继平，梅亦蕾，朱三立

（重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044）

0 引言

随着风力发电技术的不断发展，风电在电力需求中所占比例越来越大［1］。风电场穿透功率的不断加大，威胁着电力系统安全、稳定、经济、可靠运行［2］。对风电功率进行准确预测可以减少电力系统运行成本和旋转备用，提高风电穿透功率极限，有利于调度部门及时调整计划，从而减轻风电对电网的影 响［3］。

风电功率预测根据预测模型的不同分为物理方法、统计方法和学习方法。物理方法是基于数值天气预报的方法，该方法不需要大量历史数据，但需要准确的数值天气预测数据和风电场周围详细的物理信息［4］；统计方法主要有时间序列法（ARIMA）［5］、卡尔曼滤波法［6］、灰色预测（GM）法［7］、空间相关法［8］等；学习方法［9-14］能更准确拟合非线性关系，用于风电功率预测的学习方法主要有神经网络法［9］、小波分析［10］、支持向量机（SVM）［11］等。

以上每种方法都各有优劣和不同的适用场合，不可能在任何情况下都有较好的预测精度。因此采用组合预测方法对风电功率进行预测，可以充分利用各种单一模型的信息，有利于提高风电功率预测精度［15］。

组合预测方法的关键是确定各单项预测模型的权系数。有大量文献在求取权系数时，根据某一优化准则来构建组合模型，进而求得组合预测权系数，例如文献［16］和文献［17］根据最小方差确定组合模型权系数；文献［18］依据误差平方和最小的原则得到权系数；文献［19］通过平均绝对误差最小准则计算各单项模型的权系数。不同的优化准则对应不同的权系数，它并不能改进其他评价准则［20］，因此有必要综合考虑不同优化准则的权系数。故本文将不同优化准则的组合模型进行组合，进而建立新的优化模型。

本文提出了风电功率预测的优化模型。首先计算常用的6种单项预测方法的贴近度，选择贴近度大于0的单项预测方法构建组合模型；然后利用择优的单项预测模型以平均相对误差MRE（Mean Relative Error）最小、平均绝对误差 MAE（Mean Absolute Error）最小以及均方根误差RMSE（Root Mean Squared Error）最小为优化准则分别建立组合模型；最后将3种组合模型进行优化组合，利用灰色关联度分析方法得到每种组合模型的权系数，进而得到优化模型。

1 单项预测模型的选择

风电功率预测的方法较多，每种预测方法都有其特点，组合预测方法能结合各单项预测方法的优点，从而提高预测精度。但并不是所有的组合方法都能提高风电功率预测精度，当单项预测方法本身预测误差较大，由它构成的组合方法的预测精度可能比构成该组合方法的其他单项预测方法低，预测效果未得到改善，因此选择合适的单项预测模型至关重要。针对上面的问题，本文提出了一种基于贴近度的单项预测模型的选择方法。

1.1 最大-最小贴近度的基本概念［21］

设｛a（t），t=1，2，…，n｝和｛b（t），t=1，2，…，n｝是2个实数序列，则最大-最小贴近度定义为：

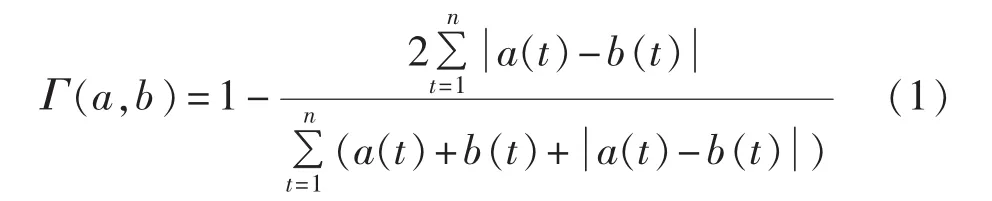
最大-最小贴近度能反映2个序列的相近程度，当2个实数序列越相近，其最大-最小贴近度值越大，其中 2 个实数序列完全相同时，即 a（t）=b（t）（t=1，2，…，n）时，最大-最小贴近度达到最大值 1。

1.2 单项预测模型的择优原理

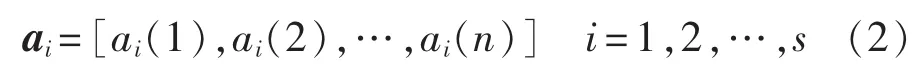
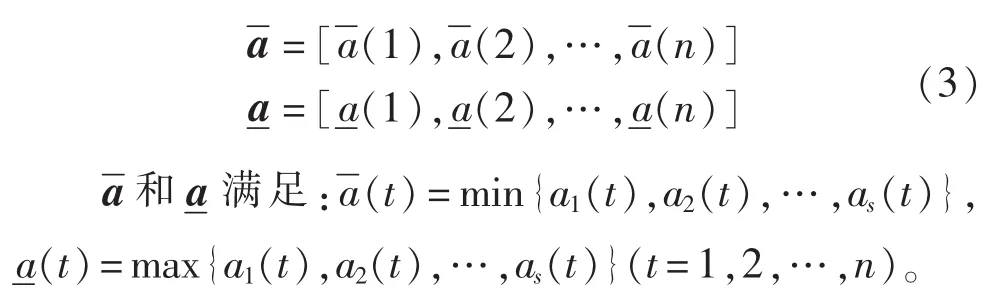
为了判断各单项预测模型的预测精度，需要考虑各单项预测模型的预测精度向量与最优点精度向量和最劣点精度向量的接近程度［22］，故引入最大-最小贴近度来表示两向量的相近程度。根据第1.1节的最大-最小贴近度可得到各单项预测模型与最优点精度向量的最大-最小贴近度和与最劣点精度向量的最大-最小贴近度）的表达式如下：

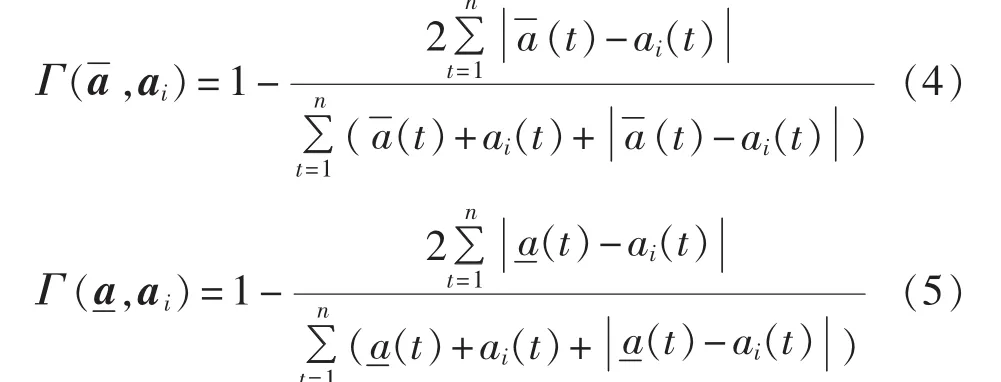
1.3 单项预测模型的选择

单项预测方法的择优之前，需要确定用于预测精度比较的单项预测方法。本文选择目前常用的6种风电功率单项预测方法，即 GM 法［23］、ARIMA［15］、BP 神经网络法、RBF 神经网络法、SVM 方法［24］、广义回归神经网络（GRNN）法［25］。

为了得到每种预测方法的预测精度向量，需要利用每种预测方法进行建模和预测。GM方法适用于处理小样本预测，即所需建模数据较少，而其他5种方法需要的建模数据较多。为了避免建模数据量带来的影响，对于 ARIMA、BP、RBF、GRNN 和 SVM方法，选择相同的数据进行模型的建立，其中在构建神经网络模型（BP、RBF和 GRNN）和 SVM模型的训练样本时，采用相空间重构的方法［26-27］，一方面能得到用于建模的训练样本，另一方面也能得到模型的输入个数，从而解决了输入个数的确定问题；GM方法的建模数据个数取为与神经网络模型和SVM模型的输入个数相同。

利用建立的6种模型，得到各模型的风电功率预测值序列，结合实际风电功率值，可得到每种预测模型的预测精度向量。根据第1.2节介绍的内容，进而得到每种模型的贴近度，选择贴近度大于0的模型进行组合预测模型的构建。

2 不同优化准则的组合预测模型

目前用于评价风电功率预测效果的常用误差指标为 MRE、MAE和 RMSE［28］。本文利用它们作为优化准则确定组合模型权系数，进而得到不同优化准则的组合预测模型。

设第1节单项预测模型的择优得到了m个算术平均贴近度大于0的单项预测模型，利用这m个单项预测模型分别构建MRE最小、MAE最小和RMSE最小的组合预测模型。

设｛y（t），t=1，2，…，n｝为风电功率实际值序列，｛xi（t），t=1，2，…，n｝（i=1，2，…，m）为第 i个单项预测模型的预测值序列，为组合预测模型得到的风电功率预测值序列，则组合预测模型的形式为：

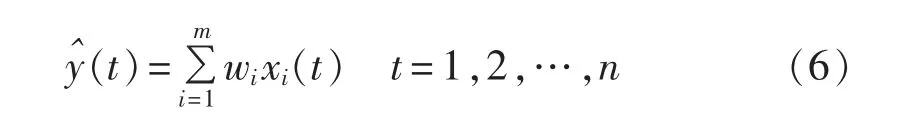
其中，w1、w2、…、wm为组合预测模型的权系数，且满足确定权系数的不同优化准则［20］如下。

a.MRE 最小，即确定 w1、w2、…、wm使式（7）最小。

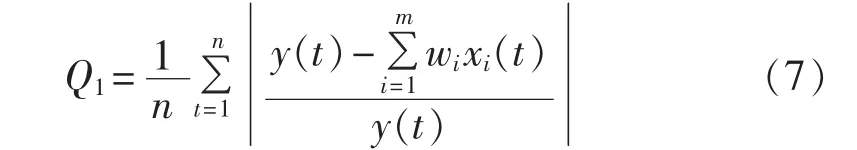
b.MAE 最小，即确定 w1、w2、…、wm使式（8）最小。

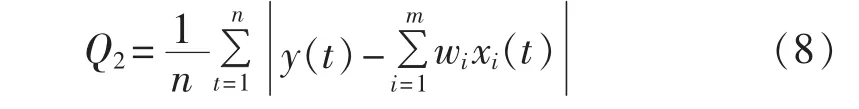
c.RMSE 最小，即确定 w1、w2、…、wm使式（9）最小。

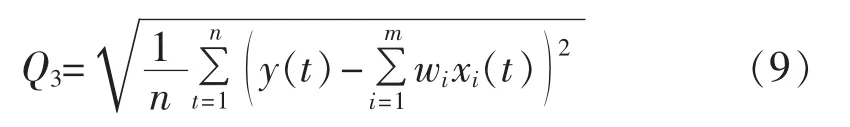
3 优化模型的权系数确定方法

第2节确定了3种组合预测模型，它们相应的预测评价指标最小，比如以优化准则MAE最小构建的组合模型对应的MAE最小，但它们并不能改进其他预测评价指标。因此，为了获得各项预测误差指标都较小的预测模型，需要将不同优化准则的组合模型（以下简称组合模型）进行组合得到优化模型。在计算优化模型中各组合模型的权系数时，本文采用灰色关联度分析方法，它充分考虑了各组合模型的常用预测评价指标，通过每个组合模型的误差评价指标（MRE、MAE和RMSE）与相关性指标（Theil不等系数和相关系数），构成的序列计算各组合模型的灰色关联度。当灰色关联度越大，说明该组合模型的综合评价指标越好，故该组合模型在优化模型中的比重应越大。

3.1 不同优化准则的组合预测模型的灰色关联度

为了计算每个组合模型综合评价的灰色关联度，需要得到各组合模型的多个评价指标。设Pi1—Pi5（i=1，2，3）分别表示第 i个组合模型的 MRE、MAE、RMSE、Theil不等系数和相关系数指标，其中Pi5=1-Ri，Ri为第i个组合模型的相关系数，这里对相关系数指标进行了修正，使它与其他指标的变化类似，即指标值越小，模型预测精度越高，为了叙述方便，仍然称Pi5为相关系数指标。以下具体介绍计算组合模型灰色关联度的步骤［29］。

a.计算3个组合模型的评价指标，它们构成了一个指标评价矩阵。

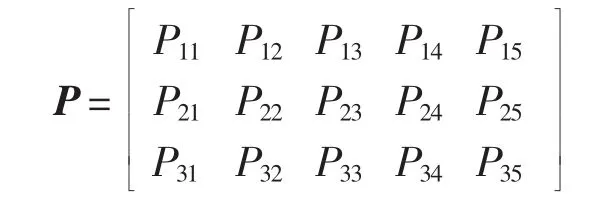
指标评价矩阵的每行对应该组合模型的指标序列。

b.确定参考序列。

利用灰色关联度分析方法进行各组合模型的综合评价时，选择各指标的最优值作为评价的参考标准，即参考序列为（P01，P02，P03，P04，P05），其中 P0j=min｛P1j，P2j，P3j｝（j=1，2，3，4，5）。

c.指标值的归一化处理。

由于各评价指标值的量纲和数量级不尽相同，为了进行比较，需要各评价指标按下式进行归一化处理。

其中，zij=（Pij-minj）/（Pij-maxj）（i=0，1，2，3；j=1，2，3，4，5），z0j=0，minj=P0j，maxj=max｛P0j，P1j，P2j，P3j｝。

d.计算各组合模型的归一化指标序列与参考序列之差的最大值M和最小值L，并得到各组合模型的灰色关联度。

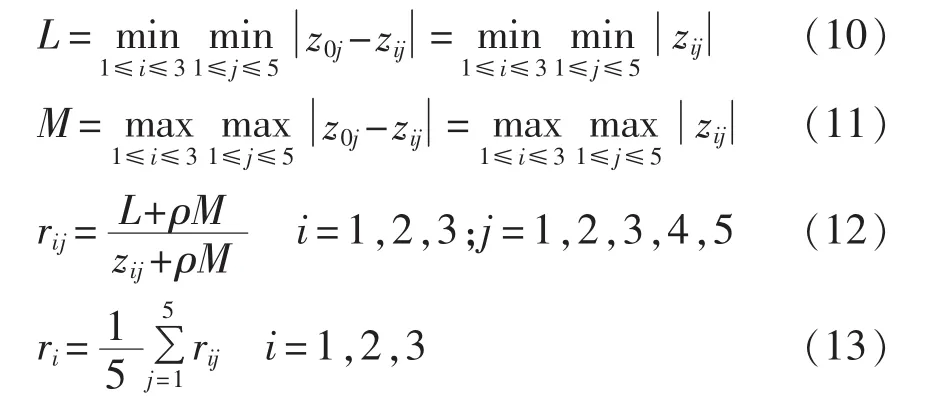
其中，ρ为分辨系数，它是M的系数或称权重，反映了系统的各个因子对关联度的间接影响程度，ρ越大，各因子对关联度的影响越大，反之，各因子对关联度的影响越小，ρ∈（0，1），通常可取 ρ=0.5；rij为第i个组合模型第j个指标与参考序列对应元素的关联系数；ri为第i个组合模型的灰色关联度。

3.2 权系数优化新方法

组合模型的灰色关联度越大，则说明该模型的综合评价指标越好，在优化模型中的比重越大，根据此原则来确定优化模型中组合模型的权系数。设为第 i个组合预测模型得到的风电功率预测值序列，则优化模型可表示如下：

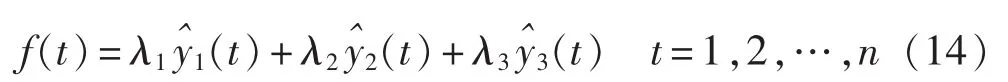
λ1、λ2、λ3根据组合模型灰色关联度可得：

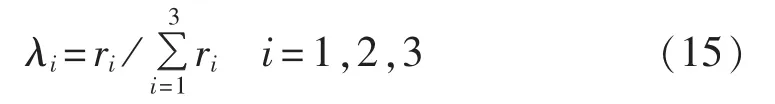
4 实例分析

本文的仿真分析是基于MATLAB软件实现的，以云南某风电场（风电场1）2012年2月1日至2月12日共12 d的风电功率数据为实验数据，数据的时间间隔为15 min，即每15 min采样一个数据点，原始数据如图1所示。

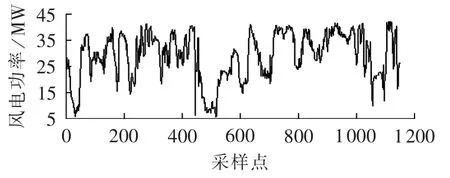
图1 原始风电功率数据Fig.1 Original wind power data

4.1 单项预测模型的选择

针对 ARIMA、BP、RBF、GRNN 和 SVM 模型，选择2012年2月1日至2月10的960个风电功率数据作为训练数据，2月11日和12日的192个风电功率数据作为测试数据。相空间重构的C-C方法可得原始数据的嵌入维数为5和延迟时间为21个采样点，故BP、RBF、GRNN和SVM模型的输入为X（i）=［x（i），x（i+21），x（i+42），x（i+63），x（i+84）］，输出为 Y（i）=x（i+85），i取值 1 至 875 对应训练样本，i取值876至1 067对应测试样本。GM模型的建模数据个数与嵌入维数相等，即利用956至960点的实际值预测961点的功率，然后用957至961点的实际值预测962点的功率，依此类推。各单项模型的结构或参数设置如下：时间序列法的模型为ARIMA（5，1，10），即差分阶数为 1，自回归阶数为 5和滑动平均阶数为10；灰色预测模型为 GM（1，1），即一阶一元灰色预测模型，建模数据为预测点前的5个数据；BP神经网络的结构为5-12-1，即输入层单元数为5，隐含层单元数设置为12，输出层单元数为1，其中隐含层为双曲正切函数（tansig），输出层为线性函数（purelin），采用的训练算法为L-M算法（trainlm）；RBF神经网络的隐含层个数根据设置的期望目标值0.001自适应确定，其中径向基函数的扩展常数取为10；GRNN可根据试验法得到最佳平滑参数σ为0.1；SVM的核函数选为高斯径向基函数，不敏感系数ε设为0.01，通过交叉意义下的网格搜索法可得到最佳惩罚因子c=45.254 8和核函数参数γ=1/σ2=0.0220971。

根据6种模型的192个点的预测值和实际值，计算得到各种单项预测模型的贴近度，结果如表1所示。

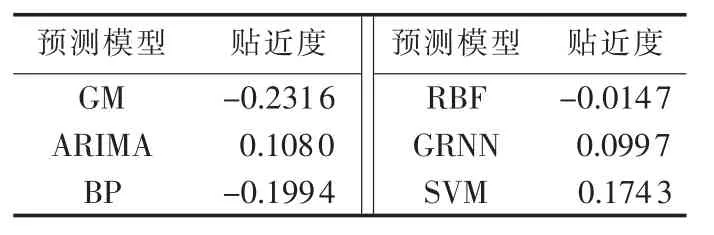
表1 各单项预测模型的贴近度Table 1 Approach degree of single forecasting models

分析表1可知，贴近度为正的单项预测模型为ARIMA、GRNN和SVM模型，故选择它们构建组合模型，预测结果见图2，预测误差见图3。为更加清晰地看出单项预测模型的预测效果，将整体预测效果图2中2个采样时间段（1至20点和110至130点）进行放大显示。

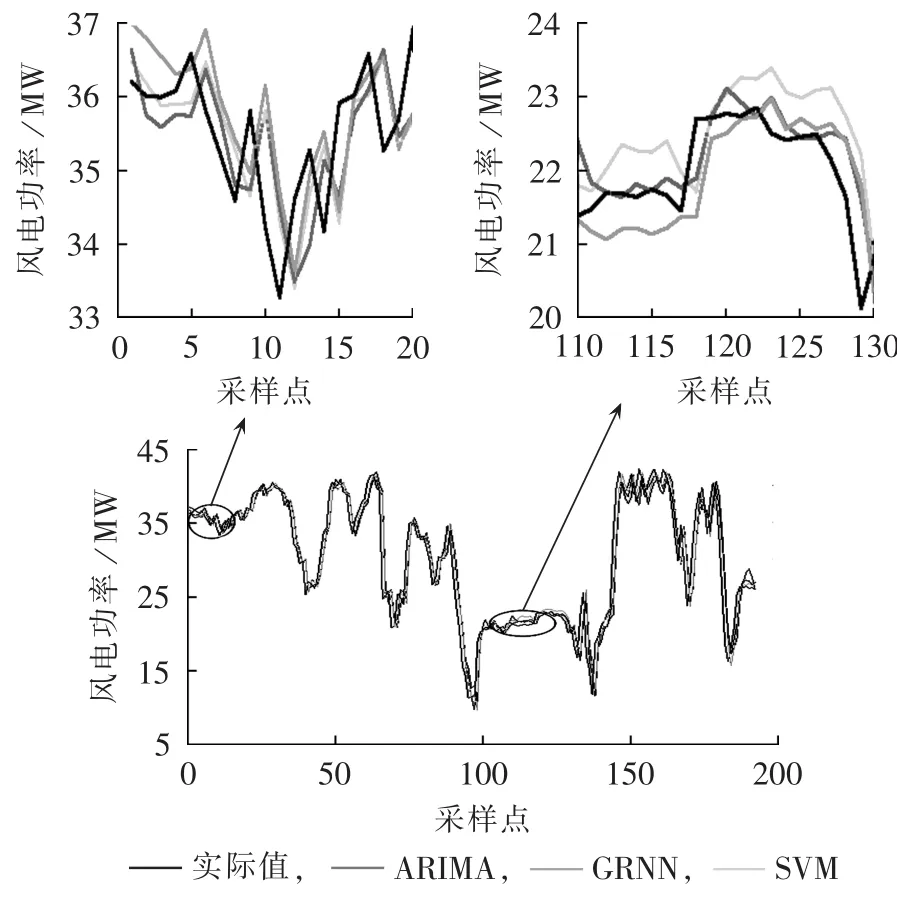
图2 3种单项预测模型的预测结果Fig.2 Forecast results of three single forecasting models

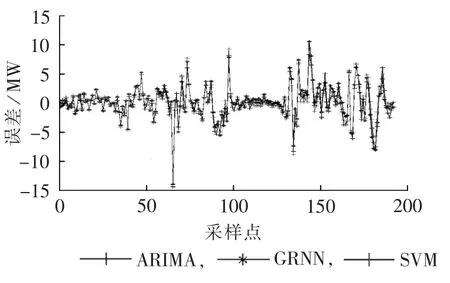
图3 3种单项预测模型的预测误差Fig.3 Forecast errors of three single forecasting models

从图2可知，ARIMA、GRNN和SVM都能跟踪实际风电功率的走势，但都存在一定的滞后性。利用 MRE、MAE 和 RMSE、Theil不等系数 δTheil和相关系数δCC分析它们的预测效果，评价指标见表2。分析表 2知，GRNN、ARIMA和 SVM的各项误差和Theil不等系数依次减小，相关系数依次增大，从而说明SVM的预测效果最好，ARIMA次之，GRNN的预测效果较差。尽管SVM的整体预测结果较好，但从图3可看出其在某些点仍然出现较大的误差。

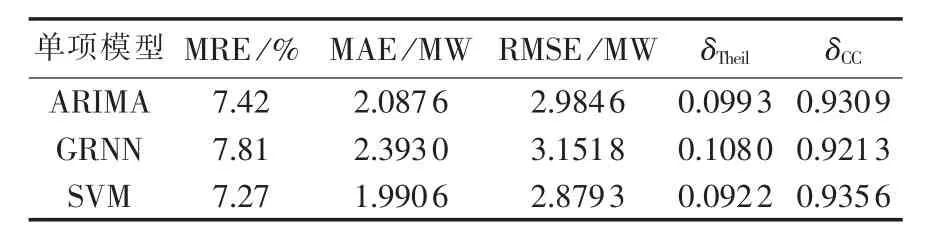
表2 3种单项预测模型的预测结果分析Table 2 Forecast result analysis for three single forecasting models

4.2 3种组合模型

以MRE最小、MAE最小和RMSE最小为优化准则确定的组合模型分别记为组合模型1、组合模型2和组合模型3，它们的预测评价指标如表3所示。

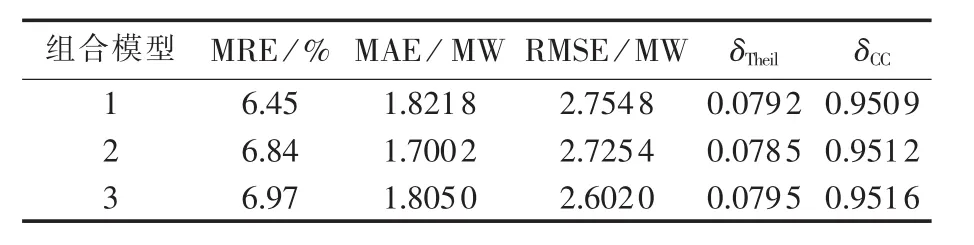
表3 各组合预测模型的预测结果分析Table 3 Forecast result analysis for combination forecasting models

从表3可知，3种组合模型的各项误差和Theil不等系数都比单项模型小，相关系数都比单项模型大，说明了3种组合模型的预测精度都得到提高。把3种组合模型每种误差的最小值称为该指标的最优值，以某种优化准则建立的组合模型对应的误差指标最小。

4.3 优化模型的预测效果分析

根据第3.1节计算3个组合模型的灰色关联度分别为0.5604、0.6983和0.7333，所以优化模型中它们的权系数分别为0.2813、0.3506和0.3681，进而得到优化模型的预测效果如图4所示。

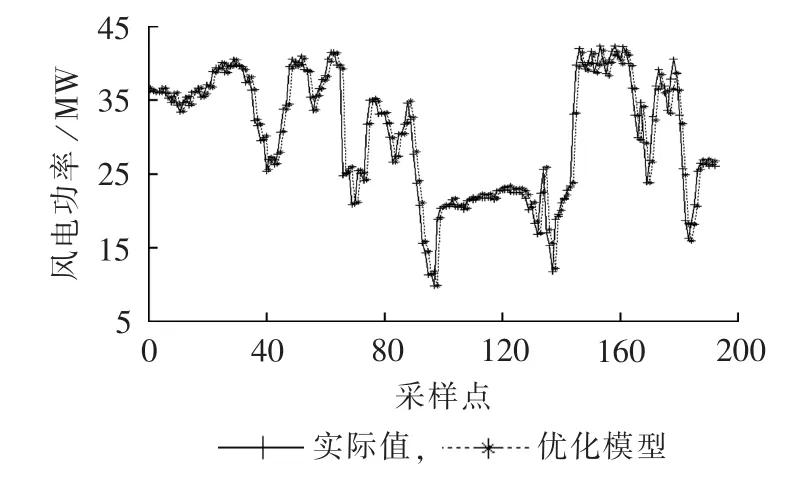
图4 优化模型的预测结果Fig.4 Forecast results of optimized model

为了更好地说明本文优化模型的有效性，分别采用等权重组合法、方差倒数法和熵值法对风电功率进行预测，并将各组合模型的评价指标列于表4。

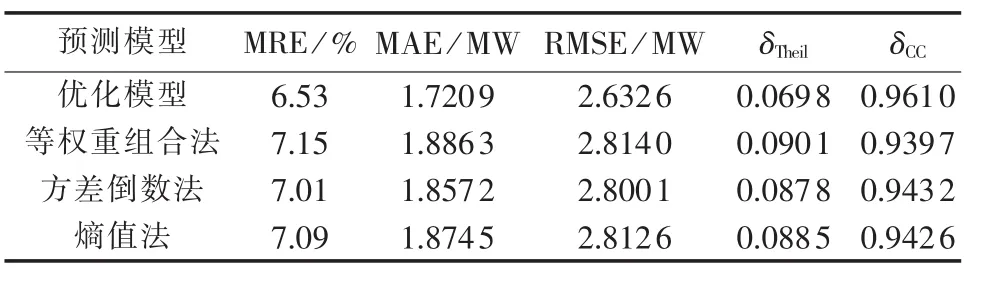
表4 优化模型和其他组合模型的预测结果分析Table 4 Forecast result analysis for optimized model and other combination models

由表4得知：优化模型的各项指标都优于其他3种组合模型，预测精度得到提高。

分析表3和表4可知：

a.优化模型的预测评价指标值MRE大于组合模型1，MAE大于组合模型2，RMSE大于组合模型3，这是符合客观事实的，因为组合模型1、组合模型2和组合模型3是分别建立在MRE、MAE和RMSE最小原则的基础上的；

b.优化模型的各项误差仅大于3种组合模型的最优值，并且与最优值相差很小，这是因为优化模型是不同优化准则的组合模型的线性组合，它兼顾了组合模型1的MRE最小、组合模型2的MAE最小和组合模型3的RMSE最小的优点，使得各项误差评价指标都较好；

c.优化模型与3种组合模型相比，Theil不等系数减小和相关系数增大，说明了优化模型较3种组合模型，预测精度得到提高。

分析表2和表4可知：优化模型与各单项预测模型相比较，优化模型的各项误差和Theil不等系数减小，相关系数增大，由此可得出兼顾不同优化准则的风电功率预测模型能有效提高预测精度。

为检验本文优化模型的适用性，选择广州某风电场（风电场2）2011年5月1日至5月12日的数据进行建模和预测，该风电场的数据间隔也为15 min，数据波动较大，其原始数据见图5。

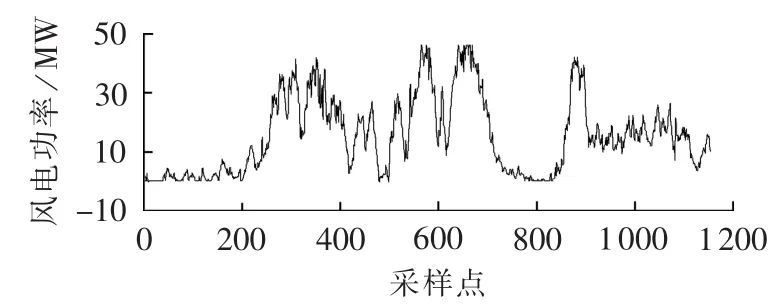
图5 原始风电功率数据Fig.5 Original wind power data

针对此风电场数据得到的贴近度为正的单项模型为RBF、GRNN和SVM，它们的预测效果见图6。

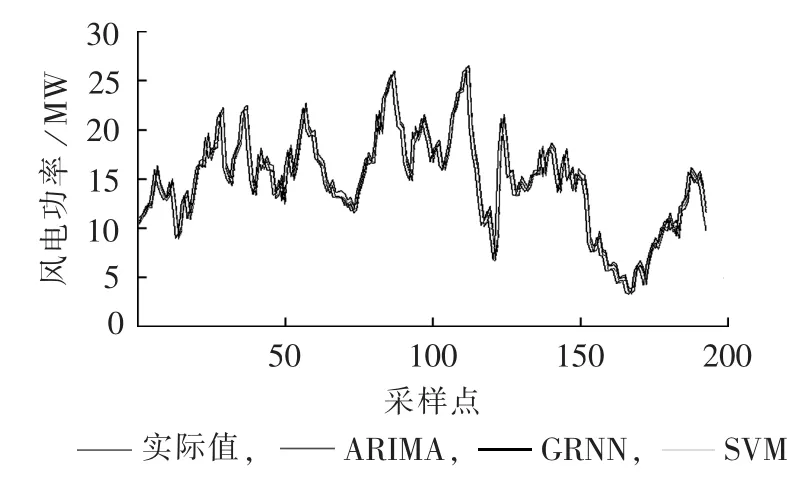
图6 3种单项预测模型的预测结果Fig.6 Forecast results of three single forecasting models

限于篇幅，本文只列出了风电场2择优的各单项预测方法、等权重组合法、方差倒数法、熵值法和优化模型的预测评价，见表5。

分析表5知，优化模型的各项指标依然优于择优的单项预测方法、等权重组合法、方差倒数法和熵值法，说明本文所提优化模型具有一定的实用性。

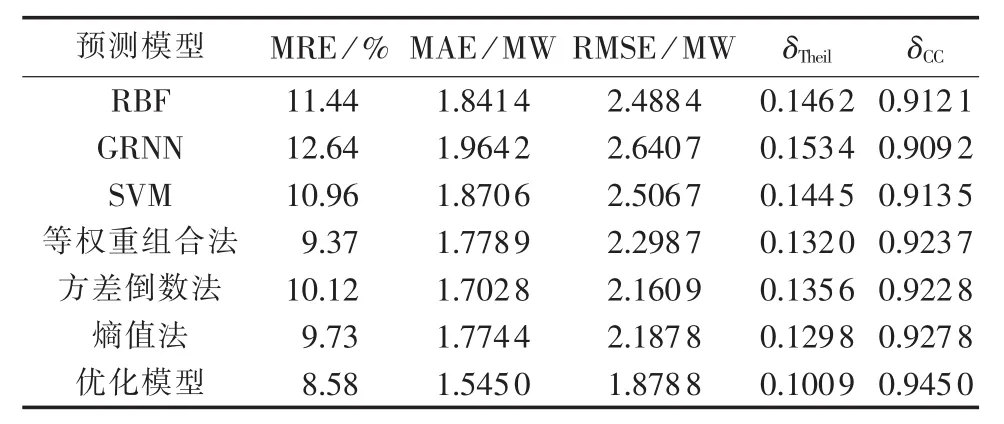
表5 各预测模型的预测结果分析Table 5 Forecast result analysis for different forecasting models

5 结论

本文通过单项预测模型的择优、不同优化准则的组合模型的建立以及优化模型权系数的确定，得到具有较好预测能力和较高预测精度的优化模型，并得到如下结论。

a.通过计算每种单项预测模型的贴近度，选择高精度的单项预测模型，一方面可以解决构建组合模型的单项预测模型的选择问题，另一方面也能使组合模型的精度提高。

b.以MRE最小、MAE最小和RMSE最小为优化准则建立的3种组合模型的预测精度较择优的单项预测模型都有所提高。

c.利用灰色关联度分析方法确定优化模型中3种组合模型的权系数，进而得到优化模型。该方法考虑了各种组合模型的综合预测评价指标，确定的权系数充分反映各组合模型预测的综合效果。优化模型同时兼顾了不同优化准则，各项预测评价指标都较好，具有较好的预测能力，能有效提高风电功率预测精度。本文的优化模型对于解决实际工程问题具有很好的应用价值。