发电机组并行恢复动态决策的熵权方法
2015-09-19梁博淼林振智文福拴
梁博淼 ,林振智 ,文福拴 ,叶 琳
(1.浙江大学 电气工程学院,浙江 杭州 310027;2.国网浙江省电力公司,浙江 杭州 310007)
0 引言
随着电力系统规模的增大和互联程度的提高,电力系统运行面临着更多不确定因素[1-6],发生大规模停电事故的可能性依然存在,因此有必要研究大停电后的系统恢复策略[7-12]。可以首先把大停电后的电力系统划分为若干子区域,然后对每个子区域根据其内的发电机组、线路和负荷状况制定相应的供电恢复方案,并根据给定的评判标准和评估方法优选最优恢复方案。在供电恢复方案的评估方面,现有文献中已经提出了一些方法[13-15],但一般假设每个恢复子区域中只有一台已恢复并具有发电能力的机组,不具备通用性。此外,现有的分区方法基本都是静态的,一般只考虑了系统恢复开始时的系统状况,而系统恢复过程是难以完全预先确定的,如此确定的分区未必是最优的。
正如电力系统互联会带来备用效益等互联效益一样,电力系统恢复过程中也可以利用系统规模可能带来的效益。文献[16]提出了以系统总恢复容量最大为目标的系统全局恢复模型,但没有考虑恢复过程中相关发电机组恢复所需容量、恢复后出力、爬坡速率、机组状态(温度等)、与已启动电源的电气距离等因素的影响,对系统恢复代价以及机组恢复时间成本也没有详细模拟。现有研究注重对所提出的黑启动方案进行评估,如果将评估理念引入到黑启动方案生成过程中,则有助于在可行域中搜索最优黑启动方案。而且,将评估对象由整体的黑启动方案转变为恢复供电方案(指只包含1台供电机组和1台受电机组以及所供电力)的组合,可以把并行恢复、多机对多机的供电转化为混合整数规划问题。
熵权法自1854年由法国物理学家K.Clausius提出以来[17],一直广泛应用于各个领域的决策研究中,如地理灾害预测[18-19]、计算机科学[20]、环 境评估[21-22]等。对于电力系统恢复领域,熵权法已被应用于区域电网的备选黑启动方案比较与决策,并取得了良好的效果[23]。通过研究熵权法的原理及效用,将熵权法引入恢复决策,可以对恢复方案进行更为综合的评估,进而获得更好的恢复策略。
在此背景下,本文初步探讨了供电恢复决策评估指标用以指导恢复决策,提出了基于熵权法的电力系统恢复策略。首先描述各台发电机组的状态信息,分析已恢复机组的出力能力和待恢复机组恢复所需投入以及其恢复对全局恢复的效益。之后,建立所有可能的单机或多机恢复供电方案,每个恢复供电方案中均描述一台已启动机组对待启动机组的供电,并利用熵权法判别所有恢复供电方案的相对优劣,为解决遴选过程中不同机组的需求冲突提供参考依据。最终的恢复策略由数个互不冲突的恢复方案构成,本文以偏离度最小为目标,考虑机组出力约束的情况下,建立了机组并行恢复动态决策的混合整数线性规划(MILP)模型,以协调恢复过程中不同机组间的需求冲突。最后,用新英格兰39节点系统对所提出的模型和策略进行了说明。
1 恢复决策问题简述
在电力系统恢复决策的问题中,对于每个恢复供电方案,为比较其对于电力系统恢复的弊益,首先需选取用于描述各台机组状态信息的指标,分析其对全局恢复的影响。从总体上而言,指标可分为效益型和成本型2类,其中效益型指标的值越大越好,成本型指标的值则越小越好。
1.1 已恢复机组的供应能力
对于已恢复供电机组,影响其对系统恢复贡献度的重要指标主要有2个:可供功率和向其他待恢复机组供电的困难程度(这里用这2台机组之间的开关设备数目表示)。设已恢复机组有n台,待恢复机组有m 台,用 Pi(i=1,2,…,n)表示已恢复机组 i的可供功率,Nij(i=1,2,…,n;j=1,2,…,m)表示从已恢复机组i到待恢复机组j之间的开关设备数目。
1.2 待恢复机组的出力能力(效益型指标)
在选取优先启动的待恢复机组时,需要考虑其出力能力以确保该机组的优先恢复对全局恢复最为有利。对于待恢复机组j,影响其对系统恢复贡献度的主要指标包括:机组状态yj、恢复后可供功率Pj、机组爬坡率aj。机组状态描述了机组的温度,即启动的难易程度,这里将其量化为9级,其中1表示极冷,3表示冷,5表示温热,7表示热,9表示极热。这些指标属于效益型的。
1.3 待恢复机组的需求(成本型指标)
在选取优先启动的待恢复机组时,也需要考虑其需求情况(即成本型指标)以确保现有恢复资源可以得到最有效利用。对于待恢复机组j,影响其系统恢复代价(成本)的主要指标包括:恢复所需功率Sj和到对其恢复供电的恢复机组i之间的开关设备数目Nij。这些指标属于成本型的。需要指出,影响恢复路径的因素除了开关设备数目外,还有其他一些重要特性,如所经变电站的重要程度、线路容量等。作为一项初步的研究工作,本文暂时没有考虑与路径相关的其他重要特性,只考虑了开关设备数目对恢复路径的影响。不过,本文所构造的方法框架可以容纳对其他重要特性的考虑。另一方面,与路径相关的其他重要特性之间一般具有一定的耦合关系,如果要将这些作为评估指标,就需要对它们之间的耦合关系进行分析,以获得更为可靠的评估结果。如何适当考虑与路径相关的其他重要特性是值得研究的重要问题。
2 基于熵权法的并行恢复动态决策模型
2.1 熵权法
首先按照熵和熵权的概念对发电机组指标进行标准化处理[23]。
设恢复供电方案的组合数为v,且影响每个恢复供电方案的指标有u个,根据实际指标构建的评价矩阵为R′,r′cd表示第d个方案的第c个指标值,则:
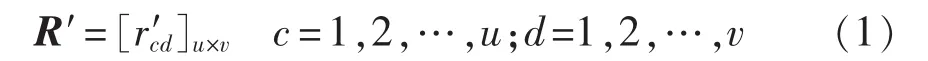
前已述及,指标可分为效益型和成本型2类。设I1为效益型指标集合,I2为成本型指标集合,则可对作如下的标准化处理:

然后,可按下面的定义1和2分别计算各指标的熵和熵权[24]。
定义1 在具有u个评价指标和v个待评价方案的决策问题中,第c个评价指标的熵Hc定义为:
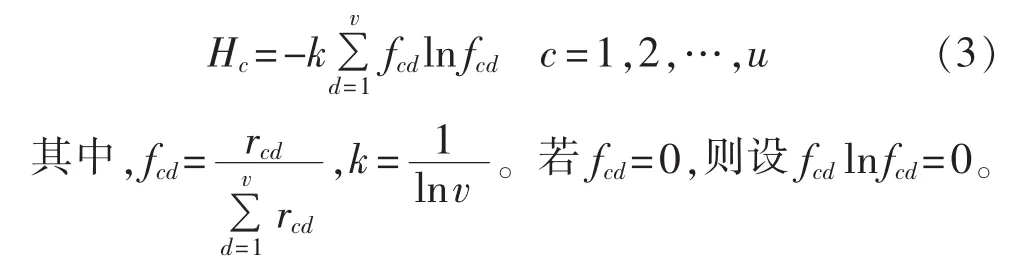
定义2 在具有u个评价指标和v个待评价方案的决策问题中,第c个评价指标的熵权wc定义为:
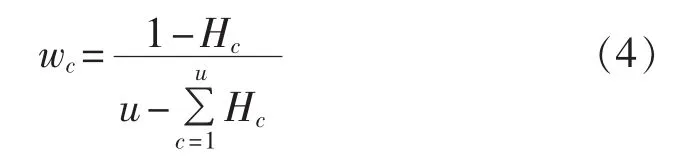
在对方案进行评价时,通过综合考虑主观的专家权重和客观的熵权确定最终的权重系数λc。假设根据专家经验确定的主观权重为Ec,则:
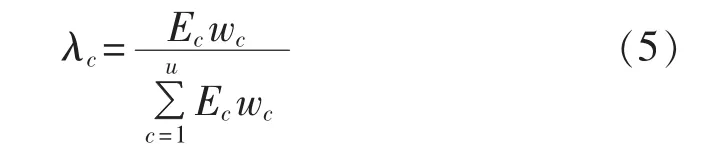
主观专家权重在很多评估预测领域得到应用,其相关研究成果包括主观权重误差的抑制以及其偏差或波动对评估结果的影响等。在权重确定过程中可以借助直觉模糊距离判据获得符合一致性的专家评估值[25],也可以通过检测等方法完善专家评估结果[26]。主观专家权重的波动会对优化结果产生影响;文献[23,25]的研究表明,采用适当的处理方法可以有效抑制主观专家权重的失真和偏颇。总之,采用主观权重与客观熵权相结合的方法可以得到更切合实际的评价结果。
2.2 基于熵权法的并行恢复动态决策模型
电力系统大停电后的恢复策略可分为串行和并行两大类。其中,串行恢复策略指待恢复机组依先后顺序启动和恢复出力的方式,决策和实施过程相对简单,恢复过程同时占用的资源较少,恢复过程中维持系统安全和稳定的压力较小,但恢复过程所需时间较长。并行恢复策略则指多台待启动机组可以同时启动和恢复出力的方式,其可以有效提升系统恢复速度,减少停电损失,但恢复过程同时占用的资源较多,恢复过程中维持系统安全和稳定的压力较大。这里提出将组合优化思想应用于并行恢复策略的确定。此外,为了协调满足不同待恢复机组的电力需求和系统稳定约束,本文在生成、设计恢复方案的过程中引入了评估方法,以实现恢复资源的优化配置。现有评估方法一般适用于对已有方案进行比较,对于方案的生成过程则关注较少。本文将熵权法用于方案生成过程,通过评估各个供电恢复方案,最终得到供电恢复方案的最优组合,即最终的并行恢复供电方案。
设共有v个已恢复供电机组向待供电机组的恢复供电方案,则v=mn。在每个恢复供电方案中,已恢复机组的主要信息为可供功率,主要用于计算其他指标,因此可不计入到影响指标中。待恢复机组的影响指标分为效益型和成本型2类:效益型指标包括恢复后可供功率、机组爬坡速率和机组状态;成本型指标则包括恢复所需功率和到向其提供恢复所需电力的已恢复机组的开关设备数目。为使熵权法适用于可行恢复方案的遴选和并行恢复方案的生成,这里引入2个新的评价指标,即指标占用比pij和反占比qij,用于反映每个恢复供电方案中待启动机组j对启动资源(即已恢复机组i)的占用率。pij和qij的定义为:
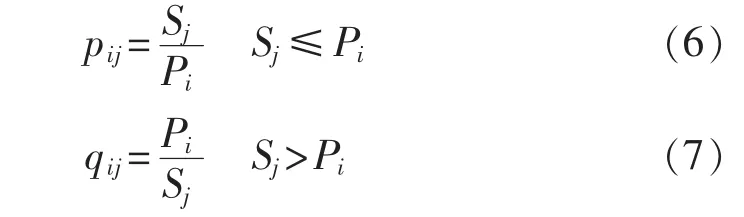
pij和qij用于反映已恢复机组向待恢复机组供电的能力。若Sj≤Pi,则表明该已恢复机组有能力满足待恢复机组的供电需求,pij反映了向待恢复机组j的供电需求占已恢复机组i的发电容量的比例;若Sj>Pi,则表明该已恢复机组无法独立承担待恢复机组的恢复供电需求,qij反映了对待恢复机组j的供电容量中已恢复机组i可以承担的比例。
然后,将所有恢复供电方案分成2组:单机恢复供电组和非单机恢复供电组。设有f1个单机恢复供电方案和f2个非单机恢复供电方案,则f1+f2=v。恢复供电方案的所有评价(影响)指标如表1所示。
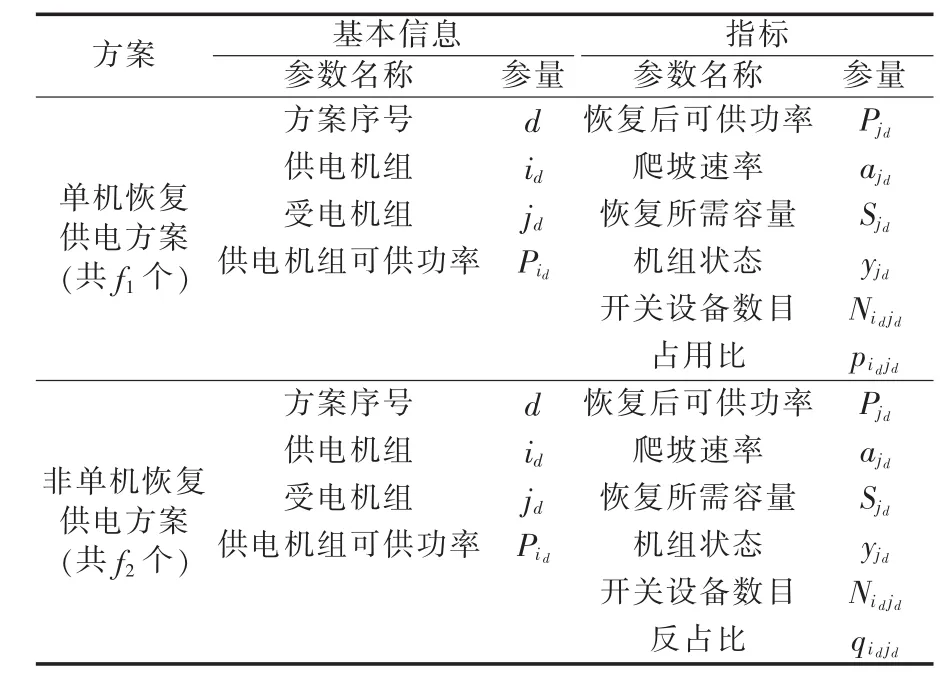
表1 所有恢复供电方案的指标集合Table 1 Index sets of all candidate restoration schemes
a.对标准化处理后的R1赋予权重,得到加权评价矩阵
b.定义理想点为所有指标取值最好时所对应的状态,而所有指标取最差值时所对应的状态为负理想点。理想点用表示。由于指标经过式(2)的标准化处理后,每个指标的最差值均为0,因此其负理想点G0=0。
c.设参加评价的恢复方案到理想点G*的距离其与理想点的偏离度为Td,则:
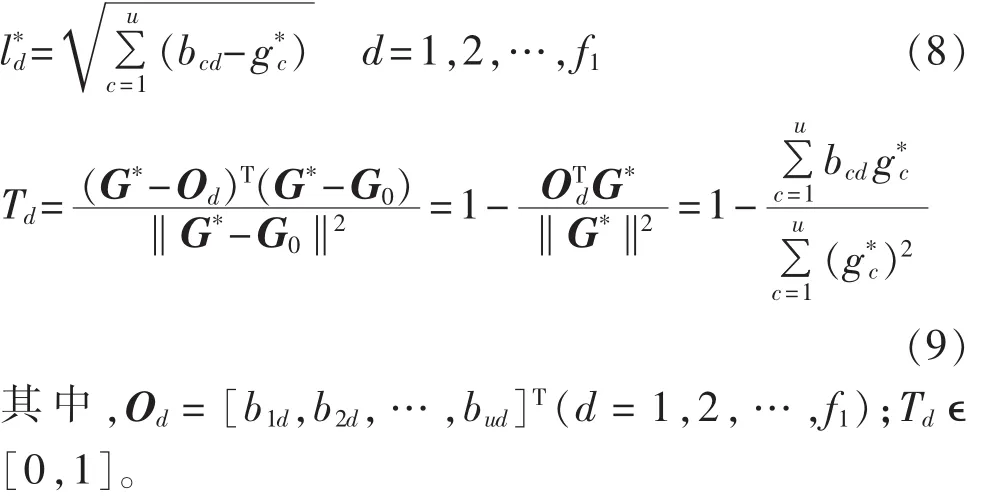
d.根据计算得到的Td值对各恢复方案进行排序,其值越小,则该方案偏离理想点越小,表明该供电恢复方案越靠近理想点。如果有2个或多个恢复方案的Td值相等,则对这些恢复方案到理想点G*的距离进行比较,距离越小则说明该恢复供电方案距离理想点越近,故该方案较优。
这样,可得到如表2所示的基于熵权法的单机恢复供电方案的参数集合。
在充分利用已有启动容量的前提下,应尽量优先安排Td值较小的恢复方案,以尽快恢复尽可能多的发电容量。本文构造的并行恢复决策方法可以描述为组合优化问题,各子方案的Td值即为其在目标函数中的权重系数。通过求解该组合优化问题,可以有效避免并行恢复过程中的资源需求冲突,从而得到协调优化的并行恢复供电方案。设x1(d)(d=1,2,…,f1)为0-1决策变量,取1和0分别表示采用和不采用此方案。设 E(z1,z2)为判别 z1和 z2是否相等的函数,若 z1=z2则 E(z1,z2)=1;否则取 0。这样,确定最优并行恢复供电方案问题在数学上可描述为:
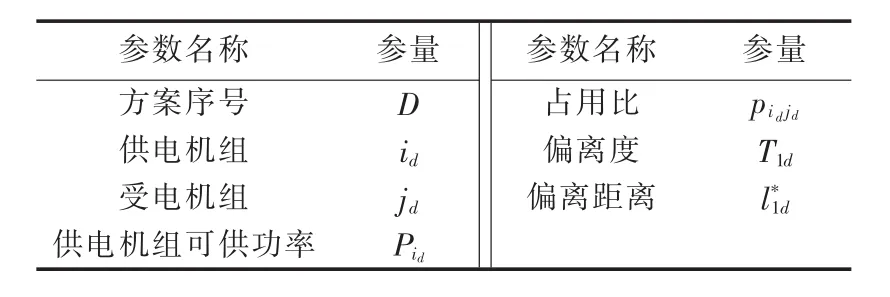
表2 基于熵权法的单机恢复供电方案相关参数Table 2 Parameters of single-unit black-start scheme based on entropy weight theory
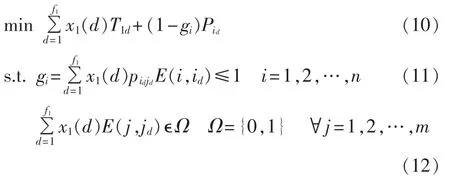
当存在多种并行恢复供电方案组合的目标函数值相同时,则将目标函数替换为后备目标函数进行计算,选取最小者为最优方案。在选定好最优并行恢复方案后,若 gi<1(∀i=1,2,…,n)或者该最优并行恢复供电方案中已恢复机组的总剩余启动容量(即除去单机恢复供电方案所消耗的启动功率后系统内剩余的启动容量)不足以启动任意一台待恢复机组,则最终决策方案即为单机恢复供电分组中优化得到的恢复方案组合;否则,需要考虑多台机组共同供电给其他待恢复机组的情形。
考虑到单机恢复供电方案组合中所占用的启动容量,将已启动机组的发电容量信息替换为已启动机组的剩余启动容量;然后,剔除在单机恢复方案中已得到恢复供电的机组,重新生成非单机恢复供电分组,得到该分组更新后的标准化评估矩阵

表3 基于熵权法的非单机恢复供电方案的相关参数Table 3 Parameters of multi-unit black-start scheme based on entropy weight theory
设x2(d)(d=1,2,…,f′2)为0~1之间的连续变量,其取值为0时表示不采用此方案,取值在(0,1]之间时表示采用此方案,且调用的功率占供电机组总功率的比例为 x2(d),即供电机组可供功率为 P′id,实际供电功率为 x2(d)P′id。在这种情形下,确定机组最优并行恢复方案问题可描述为:

基于熵权法建立上述优化模型后,首先确定单机最优并行恢复供电方案,如果仍有启动功率剩余,则更新机组信息并确定非单机并行恢复供电方案。其中,单机和非单机的并行恢复方案均是一系列供电方案的有机组合,在不发生资源占用冲突的情况下可以得到最优供电方案组合,即得到并行恢复的供电方案。确定单机最优并行恢复供电方案属于MILP问题,而确定非单机最优并行恢复供电方案则为线性规划问题。可把并行恢复决策描述为优化问题,并采用成熟而高效的商业求解器Gurobi求解[27]。
在对实际电力系统进行并行恢复动态决策时,可能需要多次调用上述优化模型。在某一步的恢复策略实施后,相关机组和电力网络的状态会发生变化。如果系统中还有待恢复机组,则需要再次调用上述优化模型,确定系统状态更新后的发电机组恢复策略,直到所有机组都被恢复为止。
3 算例与结果
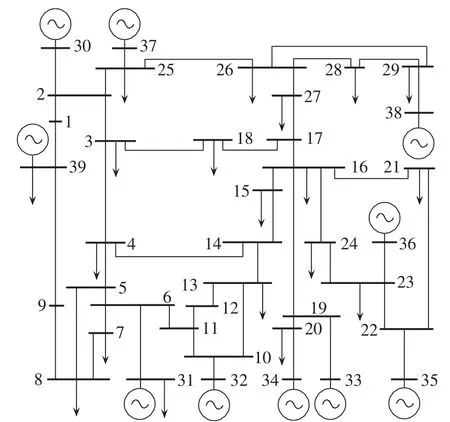
图1 新英格兰10机39节点系统Fig.1 New England 10-unit 39-bus power system
采用图1所示的新英格兰10机39节点系统,来说明所提出的并行恢复策略。假设每个发电节点只有1台发电机组,发电机组的具体参数如表4所示。假设各条输电线路的恢复时间相同,则可以通过最短路径算法求解得到恢复供电方案中2台机组之间的开关设备数目,其结果列于表5。假定大停电事故发生后位于节点30和33的机组已快速恢复,可为其他机组恢复提供电力。
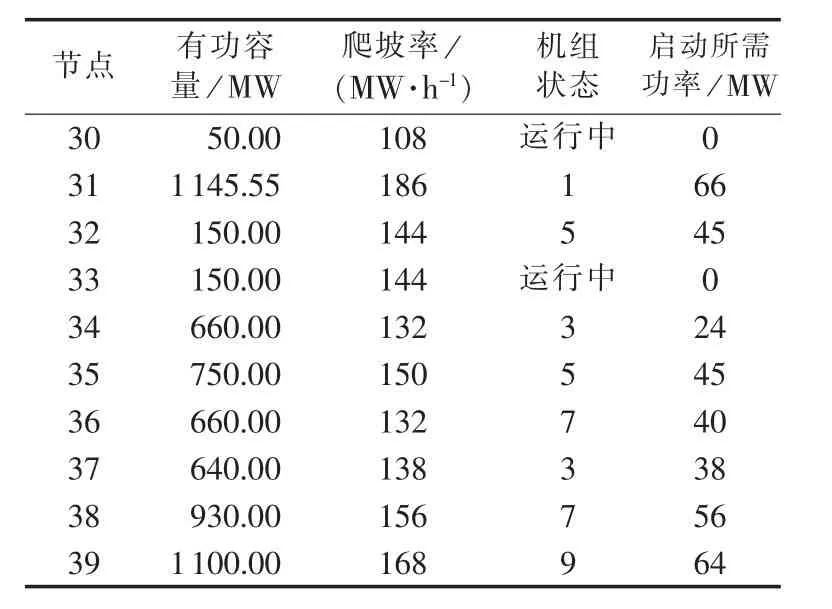
表4 各发电机组参数Table 4 Parameters of generator sets
针对该系统的网络结构和发电机组情况,可将恢复供电方案分为2组,即单机和多机恢复供电方案。计算得到单机供电恢复方案组内各指标的熵权为[0.1082,0.3155,0.0979,0.1063,0.3720]T。假设专家对各个指标赋予的权重为[0.200,0.300,0.100,0.150,0.250]T,则按式(5)计算可以得到综合权重系数为[0.0921,0.4027,0.0417,0.0679,0.3957]T。候选的单机恢复供电方案如表6所示。
针对表6列出的候选恢复方案,采用式(10)—(12)所描述的优化模型,可求得最优单机恢复供电方 案 组 合为 x=[1,0,0,0,0,1,0,0,1,0,1,0,0]T。这样,恢复供电方案为:机组30向机组32供电;机组33向机组31、35和37供电。此外,可得机组30和33的剩余启动容量分别为5 MW和1.05 MW。由于这2台机组的总剩余容量只有6.05 MW,不足以启动其他待恢复机组,此时就不存在多机恢复供电方案。
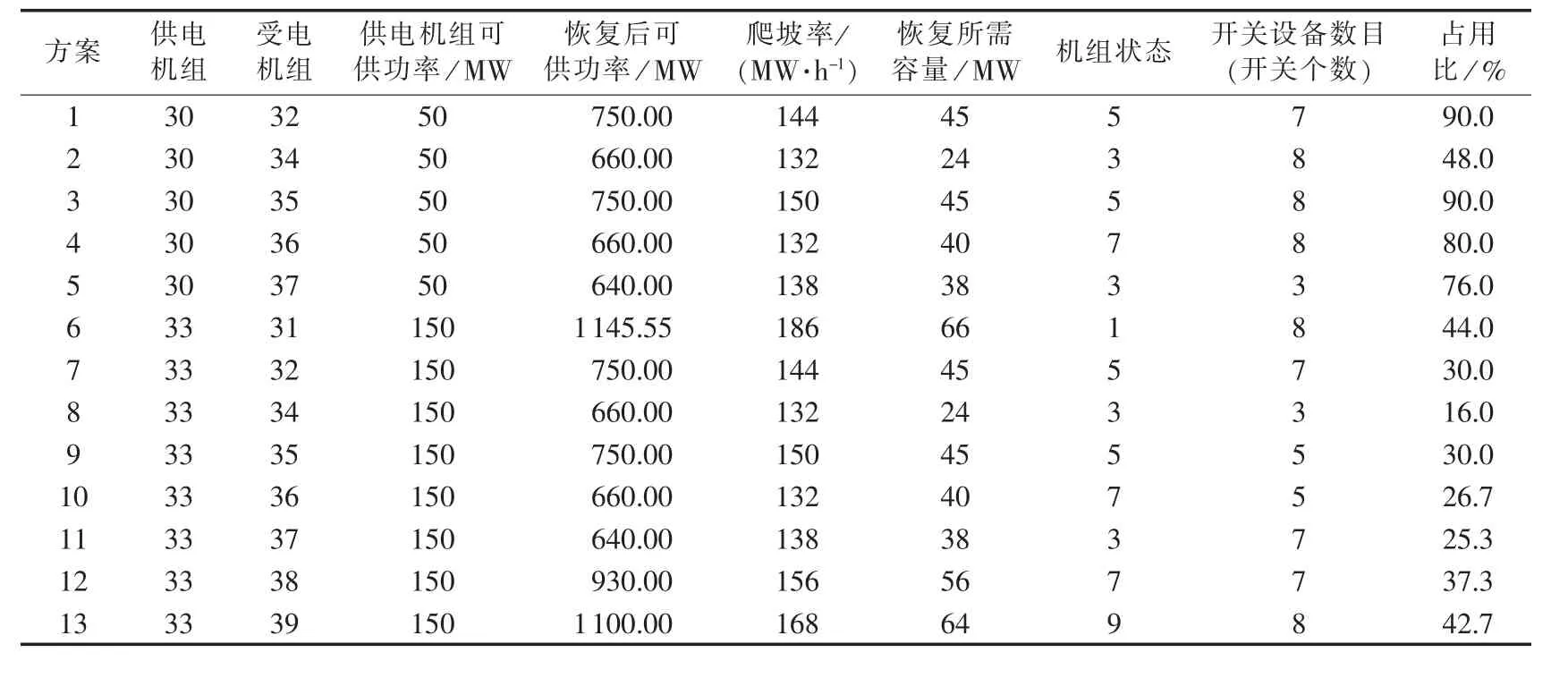
表5 单机恢复方案Table 5 Single-unit black-start restoration schemes
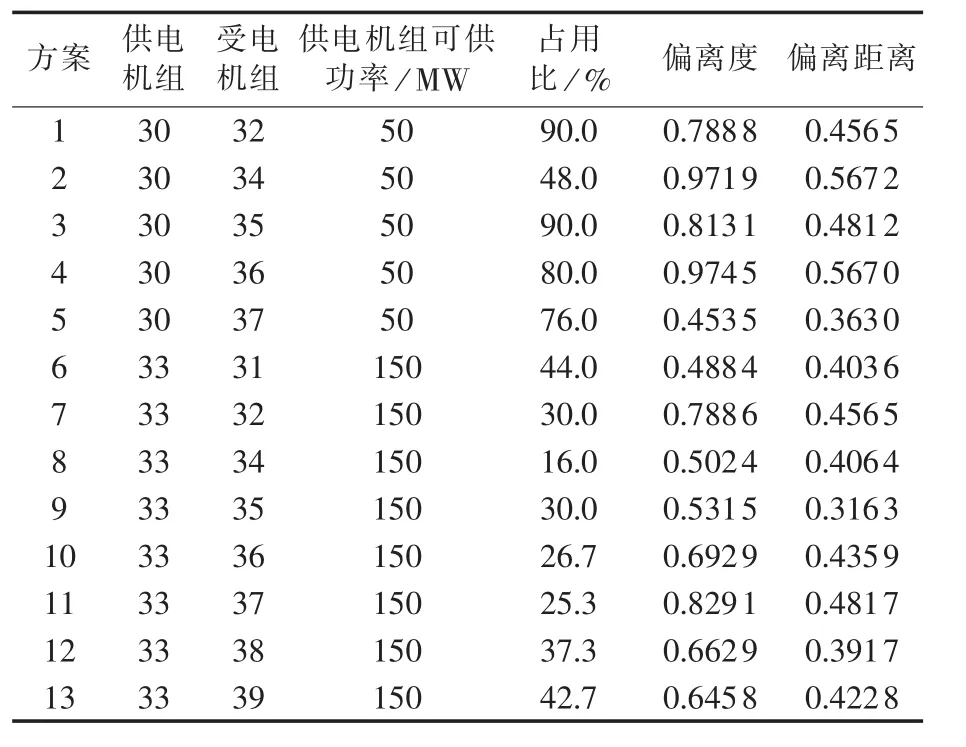
表6 候选的单机供电恢复方案Table 6 Candidate single-unit black-start restoration schemes
在当前阶段选定的目标机组得到恢复并输出功率后,就着手下一阶段的恢复决策。在当前阶段的恢复方案完成后,电力系统状态会发生变化,因此在下一步恢复方案决策前需对电力系统状态进行更新。此时,已恢复机组为 30、31、32、33、35 和 37,待恢复机组为34、36、38和39。由于多台机组已经恢复运行,因此在第二轮恢复过程中可以恢复所有待恢复机组。针对更新后的发电机组和电力系统状态信息,可求得所有恢复供电方案,表7给出了结合占用比指标筛选得到的单机最优恢复供电方案。计算可得单机恢复供电方案组的各个指标的熵权为[0.3139,0.3105,0.1297,0.1555,0.0905]T。假设专家对各个指标赋予的权重仍为[0.200,0.300,0.100,0.150,0.250]T,根据式(5)可得在该策略下综合权重系数为[0.2922,0.4336,0.0604,0.1085,0.1053]T。候选的单机恢复供电方案如表8所示。
针对表8列出的候选恢复方案,采用式(10)—(12)所描述的优化模型,可求得最优单机恢复供电方案组合为 x=[0,0,0,0,0,1,0,0,0,0,1,0,1,0,0,1,0,0,0,0,0,0]T。这样,恢复供电方案为:机组 31 向机组39供电;机组33向机组34供电;机组33向机组38供电;机组35向机组36供电。所有发电机组均得到了恢复。
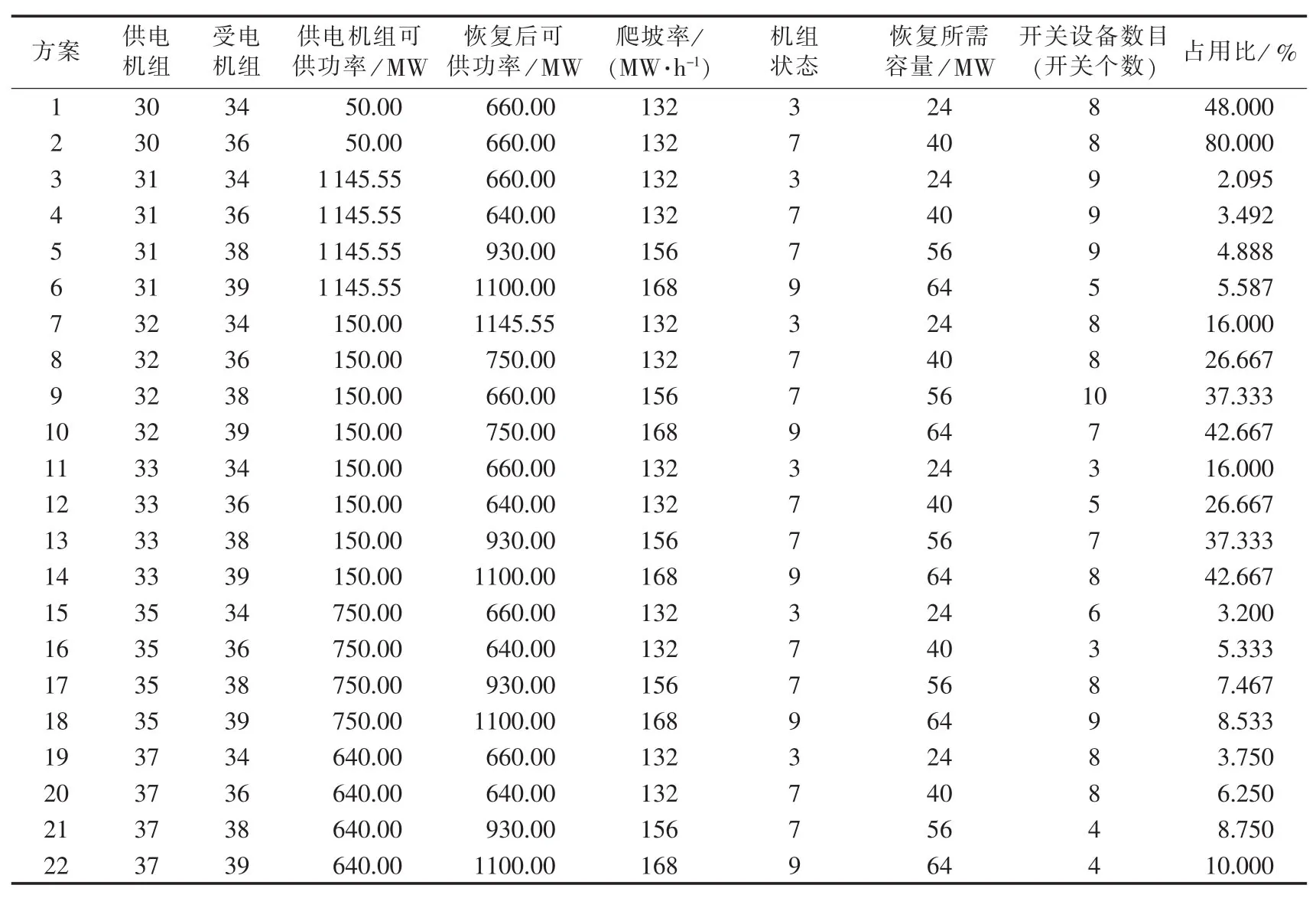
表7 状态更新后的单机恢复方案Table 7 Single-unit black-start schemes after statuses updated
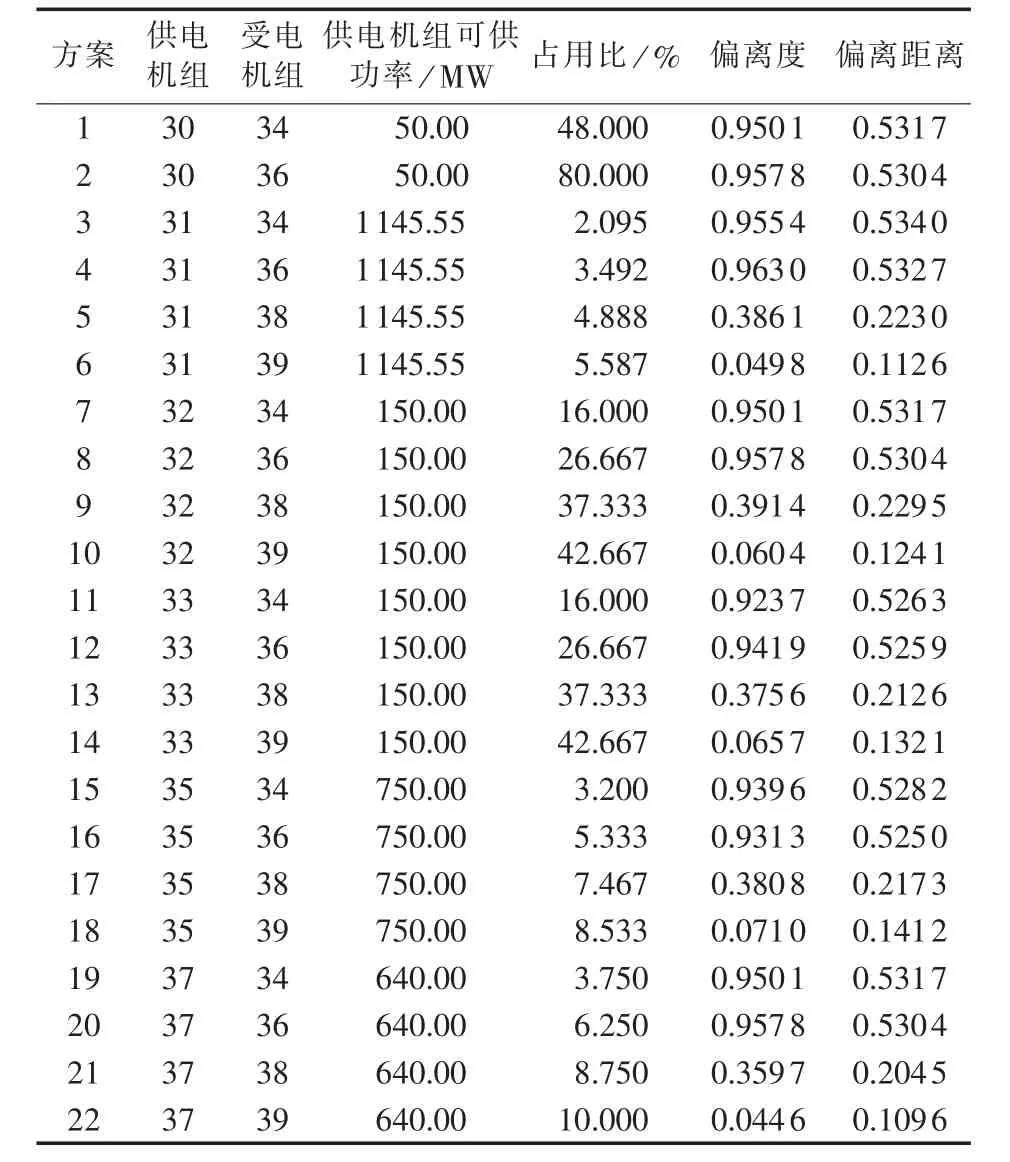
表8 状态更新后的单机恢复供电方案Table 8 Single-unit black-start schemes after statuses updated
4 结语
针对发电机组并行恢复动态决策问题,本文首先讨论了已恢复机组的供应能力和待恢复机组的状态出力能力与需求。在此基础上,以恢复全部发电机组为目标提出了基于熵权法的并行恢复优化策略的MILP模型。最后,用新英格兰10机39节点系统说明了所提并行恢复策略的可行性与有效性。
