基于ANSYS抗火分析的三面受火钢梁防火研究
2015-09-18
中建钢构有限公司华东大区 靖江 214532
1 概况
超高层建筑中对于钢结构的应用越来越多,而超高层建筑中的钢梁大多是外露的。而钢结构的耐火性能不如混凝土结构,所以我们需要对钢结构的耐火性能进行研究来制定相应的钢结构防火措施。
昆山金鹰二期大商业项目为混凝土核心筒外围劲性柱框架结构,地下3层,地上55层,结构高度251.8 m。塔楼10层以上钢梁均为三面受火的外露钢梁,耐火极限为2 h。
2 钢材材料模型建立
在钢梁防火研究中,我们以ANSYS有限元分析软件为基础,选取H型钢梁截面尺寸为300 mm×300 mm×10 mm×15 mm。考虑到现场钢梁的上翼缘为混凝土楼板,不直接受火,温度较低,故不考虑上翼缘上表面的热传导和热辐射,所以将钢梁热边界定为三面受火。荷载类型采用了跨中作用集中荷载的情况。为了较准确的模拟简支梁,且不需要考虑其在高温下的整体稳定,故在梁的一端腹板中点约束3个方向平动,另一端约束垂直梁轴线的2个方向的平动。选取荷载比为0.178和0.30,分别对应的集中力大小为100 kN和169 kN[1,2]。
温度场采用solid70单元进行热分析,此单元是具有1个自由度的八节点六面体(Brick8 node70),结构分析中转化为solid45单元。首先把模型沿梁长分成60段。腹板沿厚度分成2层,沿宽度分成10段。翼缘沿厚度分成1层,沿宽度分成12段。如图1所示。
3 热分析
3.1 温度分布
火灾下,空气与构件的热传递包括热辐射和热对流2部分,一般梁的两端有构件遮挡。故不考虑梁的两端与空气之间的热辐射和热对流。梁在三面受火条件下的温度分布如图2所示。可以看出,梁的两端温度最低。这是考虑到实际情况中的梁端部有柱子或者墙的遮挡,不会直接承受火灾的作用。三面受火下翼缘的外边缘、腹板中部温度较高。这是由于这些位置微元的辐射角系数比其他位置大,接收的热量多。

图1 钢梁有限元模型及网格划分
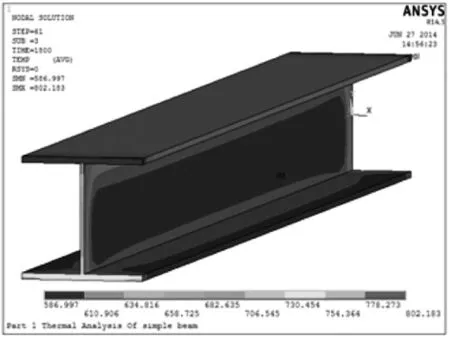
图2 钢梁三面受火温度分布
梁的跨中截面在30 min时的温度分布如图3所示,从图3可以看出,三面受火温差较大,在同一截面不同点的温度分布不均匀,沿梁轴线方向在端部有比较大的变化。三面受火温差最大可以达到200 K,这种温差将对构件截面的应力场产生很大的影响,因而也就影响到构件和整个结构在火灾下的反应[3,4]。
3.2 温度-时间曲线
由于截面温度分布不均,为了较全面地表示截面的温度-时间曲线,在三面受火钢梁上选择了如图4所示的5个点,这5个点的温度-时间曲线如图5所示(测点1对应于ANSYS中的node1,依次类推)。在三面受火钢梁的跨中截面,不同点的温差较大,随着空气的温度升高,下翼缘和腹板升温明显快于上翼缘。在1 000 s左右时温差达到最大,差值为300 K。随着构件温度升高,空气与构件温差变小,热量在构件中的热传导作用加强,温度逐渐趋于均匀。
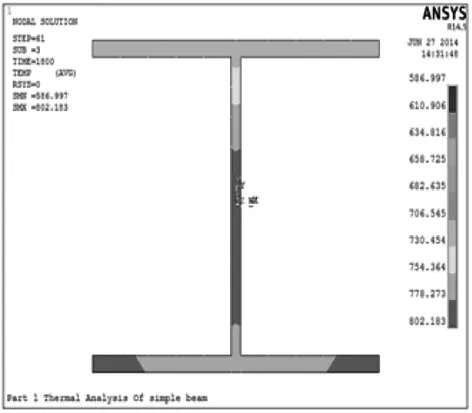
图3 钢梁三面受火跨中截面温度分布
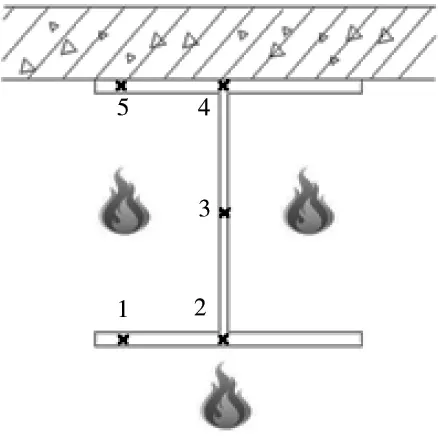
图4 钢梁三面受火温度 测点布置示意
在接近1 800 s时,下翼缘的温度-时间曲线有一拐点,即斜率有增大的趋势。腹板、上翼缘却无此现象。此时下翼缘温度约750 ℃,而腹板上翼缘及腹板温度约700 ℃时。可能是由于采用的比热容在735 ℃有一个极值点。达到此温度的地方温度上升缓慢,而超过735 ℃,比热容迅速减少,升温加快。
为了验证此假设,采用2种比热容,继续对该三面受火钢梁升温至3 200 s,得到温度-时间曲线如图6所示。从图6可以看出,各测点达到约750 ℃后,各点的温度-时间曲线都出现拐点。如果按EC3推荐的钢材比热容为定值600 J/(kg·K)重新计算构件的温度-时间曲线,则计算出的温度-时间曲线的斜率一直减少,没有出现拐点,如图7所示。
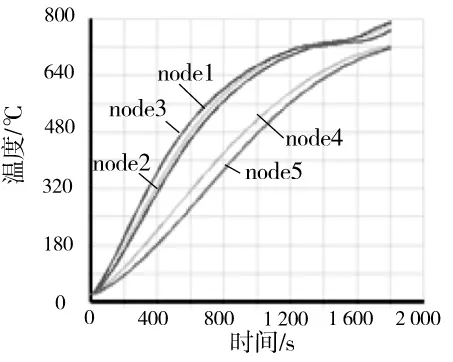
图5 钢梁三面受火温度-时间曲线
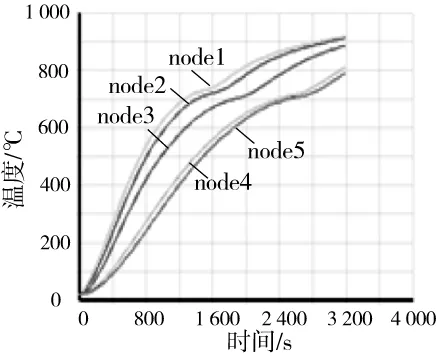
图6 EC3精确比热容计算的温度- 时间曲线
4 结构分析
对结构进行火灾下非线性分析的目的是确定火灾条件下结构的破坏机理和临界温度,以及结构的耐火时间。根据我国标准《建筑构件耐火试验方法》(GB/T 9978—2008),本实例的破坏准则为:最大挠度达到了0.05倍梁长,即150 mm。最大变形速率大于l2/900 h,即33.33 mm/s。
4.1 挠度-时间曲线
梁在三面受火下,承受100 kN的集中荷载,荷载比为0.178。在1 800 s时的变形和竖向挠度云图如图8所示。从云图可以看出,同一截面的挠度基本相等。最大挠度发生在跨中,达到了0.149 m。可以认为该梁达到了破坏。
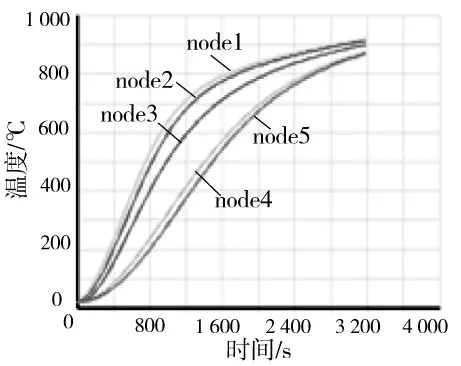
图7 EC3推荐比热容计算的温度-时间曲线
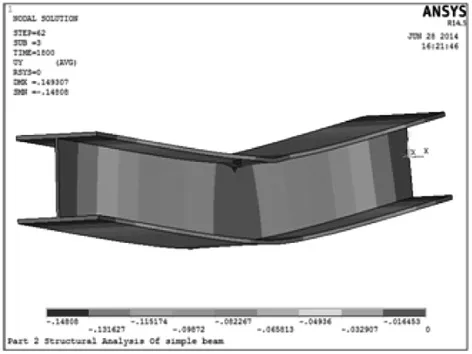
图8 钢梁三面受火1 800 s时变形 和挠度云图
跨中截面的5个测点的挠度-时间曲线如图9所示。升温过程中,荷载保持恒定,由于温度作用,梁的挠度不断增加。在升温初期(梁下翼缘温度小于400 ℃),钢材的弹性模量下降得不是很大,在400 ℃时,为常温弹性模量的70%,因此,由弹性模量弱化引起的挠度很小。同时,由于梁为三面受火,由图8可知,梁横截面上存在较大的温度梯度,而梁的端部没有约束,必然产生较大的膨胀变形。可见,在升温初期,梁的挠度增大主要由于热变形引起。升温过程中,同一截面不同点的位移在小变形下基本同步,位于集中力作用点下的测点4在1 400 s左右后的位移大于其他点。可能是由于局部应力太大,应力集中使该点的位移明显大于其他地方。在1 300 s左右,挠度-时间曲线也出现了一个拐点。这也和比热容的变化有关,此时构件温度达到了750 ℃左右,比热容急剧增大,温度上升变缓,构件刚度变化缓慢,位移出现如图9所示的一个小平台。
4.2 挠度-温度曲线
跨中截面5个点的挠度-温度曲线如图10所示,虽然同一截面各点的挠度-时间曲线差别不大,但是由于同一截面温度有一定的差别,故各点的挠度-温度曲线有较大的差别,同一挠度下,上翼缘测点4和测点5的温度比其他测点低,最大值达200 K。同一温度下,上翼缘的挠度比其他点高。在该图也可以看出,测点4的最终挠度在比同一截面的其他点的挠度大。
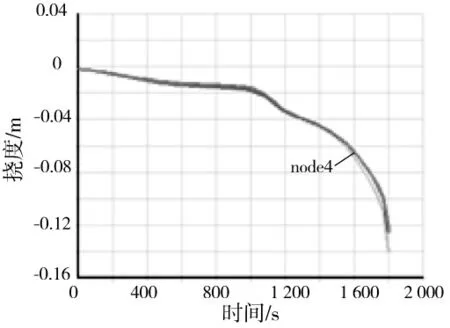
图9 钢梁三面受火5个测点的挠度-时间曲线
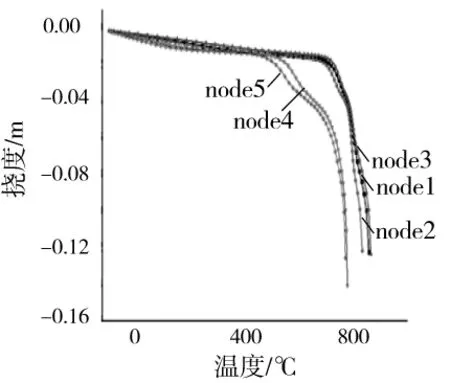
图10 钢梁三面受火 挠度-温度曲线
支座截面的5个测点的挠度-时间曲线如图11所示。在1 200 s以前,上翼缘的测点由于热膨胀位移向上,下翼缘的测点向下膨胀。而跨中测点3位于支座处,位移为零。在1 200 s以后,上翼缘位移开始向下,而下翼缘向下的位移明显加快。这是在升温过程中,梁的变形主要由热膨胀转变成主要是由材料的刚度颓坏引起。
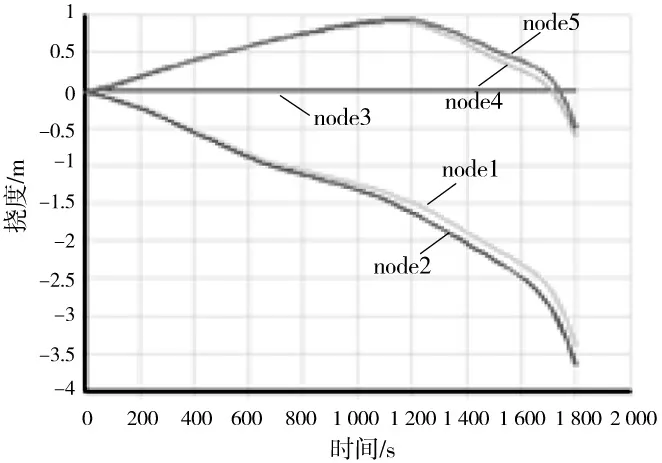
图11 钢梁三面受火端部节点挠度-时间曲线
4.3 高温下的应力
在1 800 s时,梁上应力密度如图12所示,应力绕梁轴线基本对称。在集中荷载作用点和两端支座约束点处的应力较高,在梁的端部翼缘处应力最低。
这5个点沿轴向的应力随时间的关系如图13所示。正值表示拉应力,负值表示压应力。升温开始后,由于下翼缘靠边缘测点1和腹板中部测点3辐射角系数大,受空气的辐射、对流作用强,升温较快。上翼缘和翼缘与腹板交接处的测点2、4、5升温较慢。测点1、3温度高,受热产生膨胀,测点2、4、5会约束其膨胀,故在测点1、3中产生膨胀压应力,测点2、4、5产生膨胀拉应力。所以在升温一开始,测点1、3应力降低,而测点2、4、5应力增加。随着温度的增加,截面温度分布趋于均匀,膨胀也趋于均匀,各点的应力也向初始时刻的应力靠近[5,6]。

图12 应力密度云图
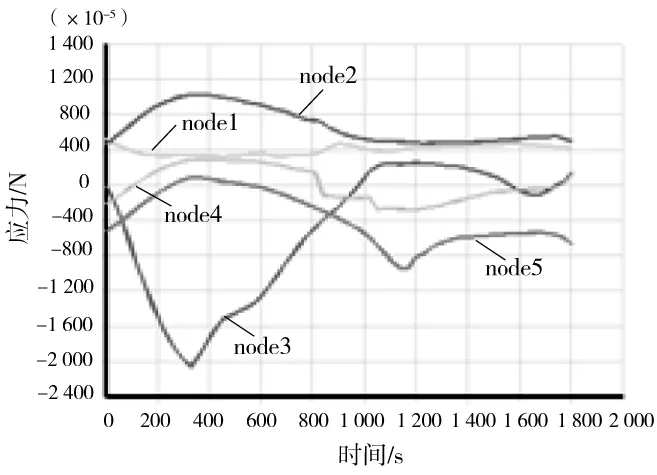
图13 梁跨中截面应力-时间关系曲线
5 结语
通过基于ANSYS进行的三面受火钢梁的抗火分析,我们发现三面受火钢梁在受火初期,截面各点温差较大,会产生自相平衡的内力,但仍然很快就会失去承载力。而且,在高温下较小的荷载就可以引起钢梁很大的变形。所以外露钢结构施工时对防火涂料的施工要引起足够的重视,以免发生火灾时对结构造成不可逆转的损害。
