考虑船舶服务优先权的泊位-岸桥分配
2015-09-18严南南上海海事大学信息工程学院上海201306
张 迪,严南南(上海海事大学信息工程学院,上海201306)
考虑船舶服务优先权的泊位-岸桥分配
张迪,严南南
(上海海事大学信息工程学院,上海201306)
为了解决泊位与岸桥的分配问题,将船舶服务优先权作为影响因子,建立以最小化船舶等待时间,作业时间以及延迟时间为目标的优化模型,以此进一步提高集装箱码头的服务质量与客户满意度。为求解此模型,设计一种遗传算法,此算法将泊位-岸桥集成分配问题分解转化为对泊位的岸桥分配主问题和船舶调度的子问题。并且通过试验算例表明,该遗传算法是有效的,并且能够相对减少船舶总的在港时间,从而提高码头作业效率。
泊位-岸桥分配;遗传算法;服务优先权;船舶调度
0 引言
泊位-岸桥分配问题是指在考虑泊位、岸桥是否空闲等的条件下,根据一定的优化策略,为到港的船舶制定靠泊时间、靠泊位置和分配岸桥的过程,其合理性将直接影响船舶在港时间、码头的运行效率以及服务水平。
Park和Kim首先提出了将泊位分配与岸桥分配结合考虑,作者离散化处理了静态连续型的泊位-岸桥分配问题,以最小化总作业成本为目标,使用拉格朗日松弛算法从而得到近似解[1]。Rashidi提出了以拉格朗日松弛算法为基础的启发式,以及动态规划决策方法,以决定泊位、靠泊时间和岸桥分配[2]。Oguz也研究了静态连续泊位-岸桥分配问题[3],他们认为这是一个并行机调度问题,最小化最迟完成时间,即所有船舶中最迟完工的时间。Imai在考虑岸桥能力的前提下,对于离散泊位进行分配,并提出了最小化船舶总在港时间的泊位-岸桥分配问题模型,采用遗传算法得出问题的近似解[4]。Liang[5]考虑了离散型泊位-岸桥分配问题,以最小化船舶总的操作时间、等待时间和延迟时间之和为目标,设定船舶的停泊时间、停泊位置和分配的岸桥数目为决策变量。Bierwirth[6]调整了Branch-and-Bound算法以结合泊位计划问题和岸桥分配问题来解决岸桥调度问题。杜玉泉[7]采用深度集成的方法建立泊位和岸桥联合调度模型,为求解此模型,采用了外逼近算法。赵坤强、韩晓龙等[8]在研究泊位岸桥分配问题时,采用了两阶段的研究方法,以最小化岸桥移动次数和船舶在港时间为目标,提出了岸桥分配和泊位分配的混合整数规划模型。
现有研究大多对于影响码头作业的因子,一般为岸桥干扰、抵达时间不确定等因素,但是对船舶自身要求较少考虑。但是在码头间竞争日益激烈的今天,更应该考虑提高客户满意度,增强自身竞争力。因此,可以选取船舶优先权作为影响因子。其中,集装箱码头可以根据船舶的具体情况,分别设定其服务优先权,例如船舶服务优先权与其装载量相关,装载量越大服务优先权越大,或者是船舶作业紧急者服务优先权较大。
对于模型的求解,大多数研究集中在泊位-岸桥的集成分配,然而,对于整体的集成问题由于其问题的复杂性可能并不有效。而充分分解的问题,不仅可以提高解决方案的质量,同时,它还可以减少计算所需的时间。所以本文设计了一种两级的遗传算法,包含对于泊位进行岸桥分配的主问题以及对于泊位进行船舶调度的子问题,并通过相互关联的遗传算法解决这两个问题。
所以,本文对于泊位与岸桥的分配问题,在建立目标函数时引入船舶服务优先权,目标函数选取以最小化船舶等待时间、作业时间以及延迟时间,从而建立泊位-岸桥调度模型。为了求解此模型,设计了遗传算法。
1 问题描述
通常,在船舶抵港之前,码头管理者会根据码头现场情况与船舶到港信息等,制定优化策略将泊位和岸桥分配给各船舶。
本文选取一段时间内港口所到达的船舶作为研究对象,引入船舶服务优先权,其中通过船舶装卸量决定船舶服务优先权,根据问题的实际情况,做出以下假设:
(1)考虑船舶离散型靠泊方式;
(2)每艘船舶有且只有一次靠泊机会,排除移泊情况;
(3)船舶到港后才能被码头服务;
(4)每艘船舶的到港时间确定;
(5)船舶开始作业后将不能被中断直至结束作业。
2 优化模型
本文引入的符号如下:
设V={1,2,…,v}、B={1,2,…,b}和Q={1,2,…,q}分别为船舶集、泊位集合和岸桥集;C为岸桥总数;对于船舶i,αi为船舶i的优先服务系数,tai为预期到港时间,tdi为船舶离港时间,ei为船舶i的装卸效率,Qmaxi为同时分配给船舶i的最大岸桥数,tgap为船舶等待作业时间不均衡上限;V0为单个岸桥的作业效率。决策变量qcj表示分配给泊位j的岸桥数目,Pik表示k号岸桥分配给船舶i的作业时间。变量thi和tfi分别表示船舶i的开始作业时间和完成作业时间。定义变量θijk,当船舶i在泊位j上被岸桥k被服务时,θijk=1,否则θi-jk=0;变量βjk,当岸桥k分配给泊位j时,βjk=1,否则βjk=0;变量mikj,当船i在船k之后在泊位j上停靠,则mikj=1,否则mikj=0。
模型的目标函数为:
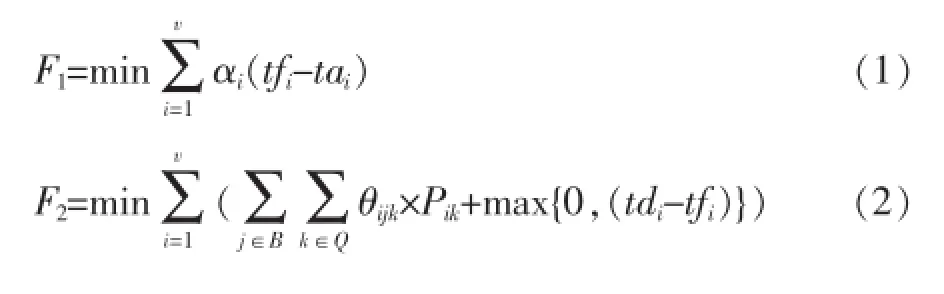
约束条件为:
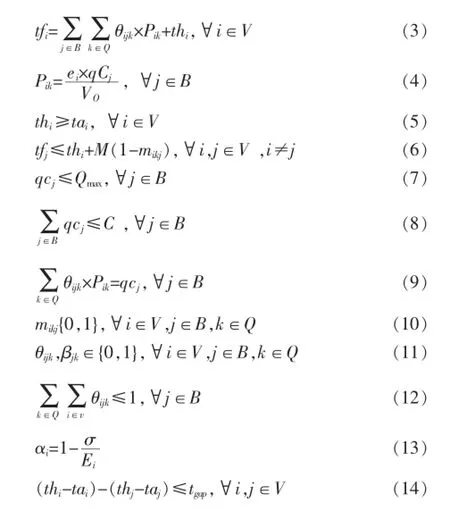
目标函数式(1)表示在考虑船舶优先权的情况对于所有船舶等待时间的和求最小。式(2)表示对船舶作业时间以及延迟时间求最小。
约束条件(3)计算了船舶完成作业的时间,约束条件(4)表示岸桥作业时间的计算方法。条件(5)和(6)保证了每艘船不能在到达时间之前停泊且不能在之前的船舶作业完成之前停泊。条件(7)保证了分配给泊位的岸桥数不超过分配的最大岸桥数。条件(8)保证了分配给泊位的岸桥数不超过可用的岸桥数。条件(9)~(11)定义了变量的计算方法。约束条件(12)保证了每个泊位一次只能有一艘船舶停泊,一艘船舶只能靠泊一次,作业完成之前不能离港。条件(13)保证了一个岸桥一次只能分配给一艘船舶。约束式(15)定义了船舶服务的优先权,其中σ表示装卸箱量对船舶调度的影响因子,σ越小,装卸箱量对船舶调度的影响越小。约束式(14)表示任意两艘船舶的等待作业时间均不超过不均衡上限。
3 模型求解
遗传算法将泊位-岸桥的集成问题分解为船舶调度问题和岸桥分配问题,并用迭代的方法求解。遗传算法包含两个部分,第一部分解决分配给泊位的岸桥问题,即为岸桥分配的遗传算法。这是个主问题,它直接决定了每个泊位的集装箱吞吐能力。第二部分是船舶调度的遗传算法,即为决定船舶分配和调度的子问题。子问题的解决方案会在之后的步骤中反作用于主问题的求解。
其流程图如图1所示。
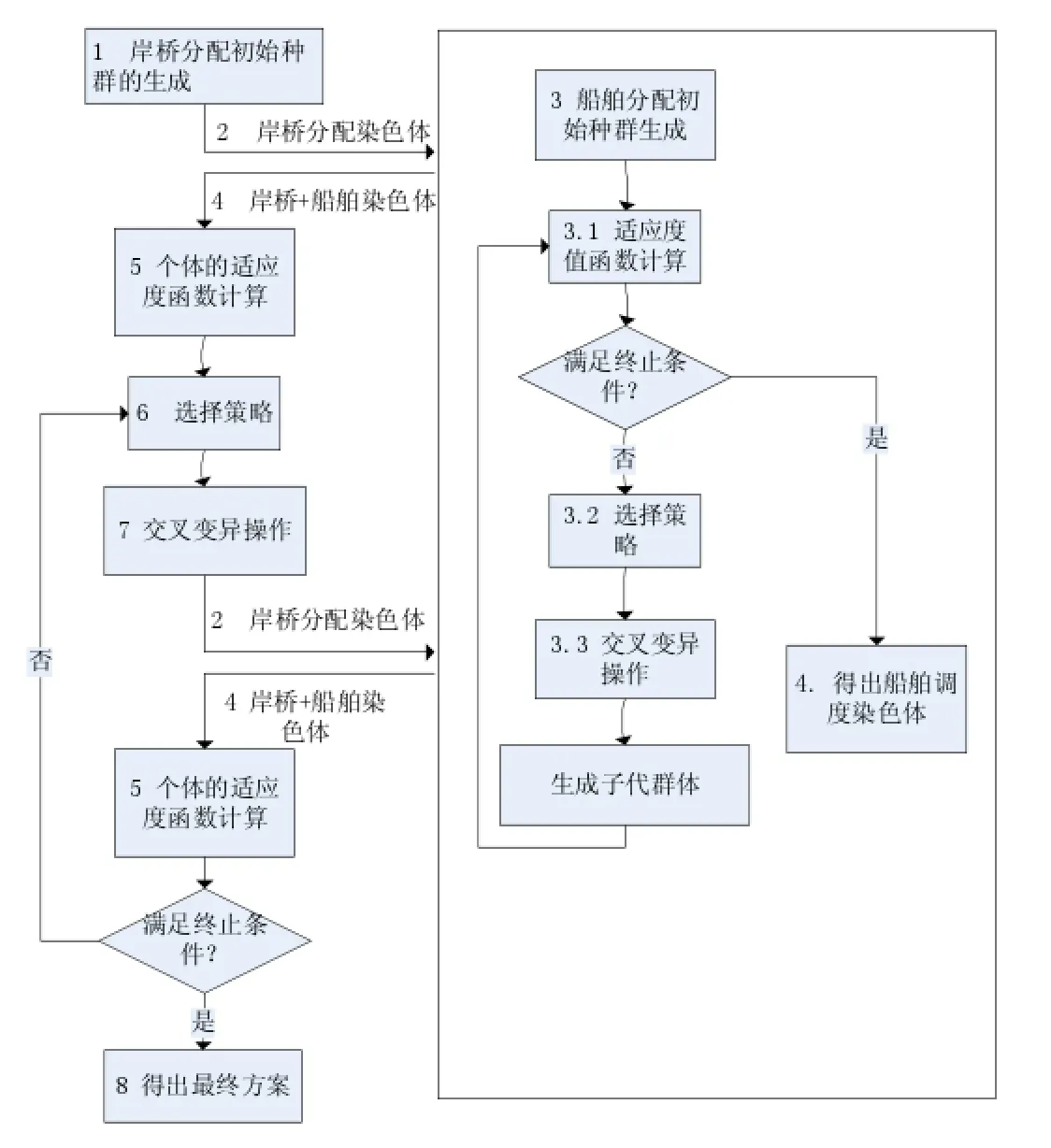
图1 遗传算法流程图
算法步骤如下:
(1)随机生成岸桥分配的初始种群,其染色体编码表示如表1所示,基因的位置表示泊位位置,且从左至右递增,基因的值表示此泊位上分配的岸桥数目。
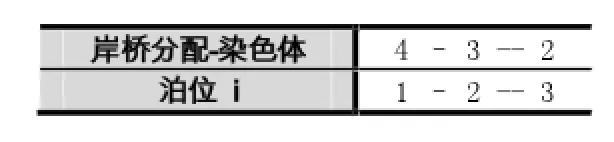
表1 岸桥分配-染色体编码
(2)每一个岸桥分配的染色体,将作为船舶调度的初始值输入。
(3)在船舶调度中,初始种群也采用随机生成的方法,其染色体编码如表2,它表示每个泊位上船舶的分配以及服务次序,其中染色体长度为船舶数目与泊位数之和,基因在编码时被0间隔,每个0表示一个泊位间隔,基因的值表示分配给此泊位的船舶号,其服务次序由左至右递增。转至Step 3.1~3.3,直到条件终止,此时得到每个岸桥分配方案下的最佳船舶调度方案。
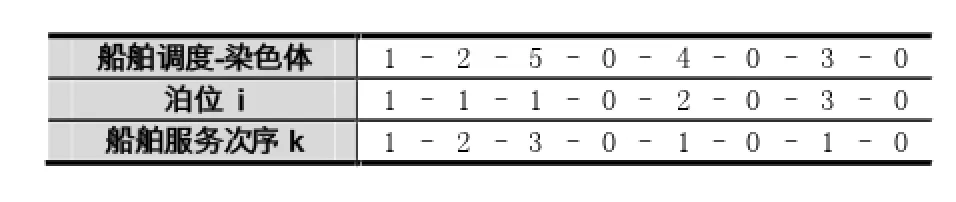
表2 船舶调度-染色体编码
①在为泊位分配的岸桥数目确定的条件下,对船舶调度的个体进行适应值计算。
②选择策略,采用轮盘赌选择法选择个体。为避免优秀染色体被淘汰,引入精英策略。
③交叉、变异操作:采用两点交叉法,产生子代。子代若不符合约束条件则调整,进而产生可行解,如图2所示。变异则是在染色体中,随机选择一个基因变异,且变异后的子代需满足约束条件。转到(4)。
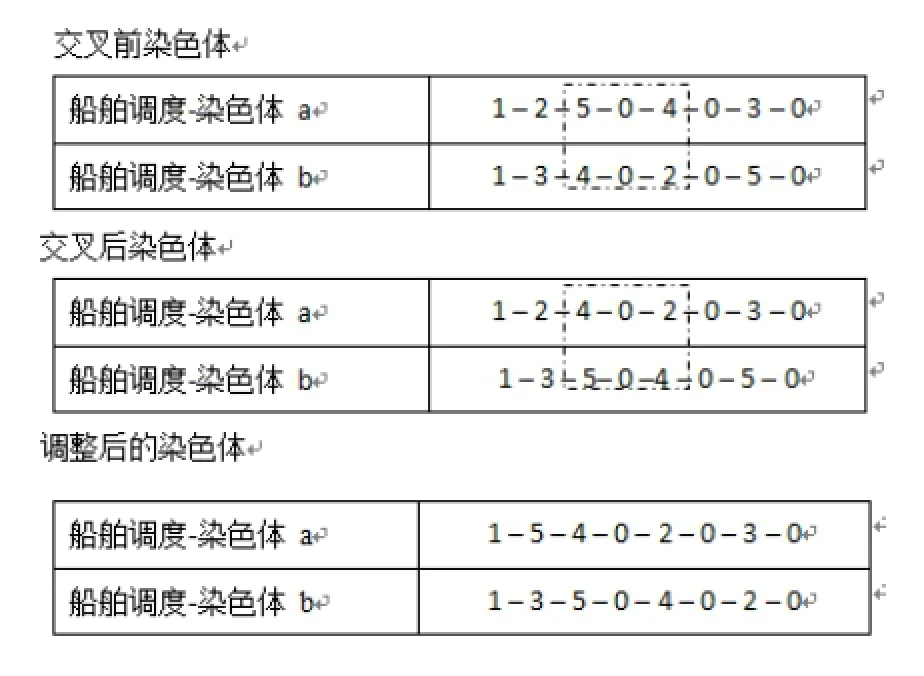
图2 船舶调度-染色体变异及调整图
(4)将船舶调度中的最优解与岸桥分配的初始解,引入到岸桥分配算法中。
(5)对于岸桥分配的个体,进行适应值计算。
(6)选择策略,采用轮盘赌选择法并且引入精英策略。
(7)交叉、变异操作:对于岸桥分配的个体采用单点交叉法,通过调整策略产生可行的子代,如图3所示。变异则采取单点随机变异。
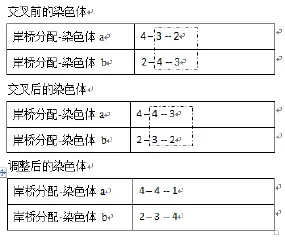
图3 岸桥分配-染色体变异及调整图
(8)确定是否达到终止条件,若达到则得出最优解,若没有,转到步骤2重复执行。本文中采用设定进化代数的方法来结束算法运算。
4 算例分析
某集装箱码连续岸线头总长1000m,岸桥7台,泊位为4个。选择以一段时间间隔的到港船舶数据。另根据码头生产经营统计数据,取v0=65箱/h。
为得出计算结果,使用MATLAB编写程序,机器配置为CPU 2.8 GHz,内存2G。在本例中,基本设置为,种群大小pop=10,σ=200,船舶等待时间作业上限tgap=10,为遗传迭代次数G=300;交叉概率Pc=0.25,变异概率Pm=0.1,从而得出的泊位-岸桥分配图,如图4。
在算法程序中,其余条件均不变,但是并不引入船舶服务优先权,即设置σ=0,得出的泊位-岸桥分配图如图5。
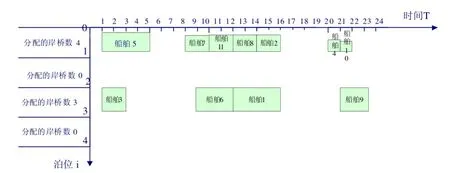
图4 σ=200时泊位-岸桥分配图
将计算结果比较,如表4,可以看出,当σ=200时的船舶等待时间要比σ=0时的船舶等待时间少,即在模型中引入船舶服务优先权,可以将船舶的等待时间减少,从而总体减少船舶在港时间,减少码头的运营成本。所以在码头的实际作业中,可以引入船舶服务优先权,更有利于提高码头的服务水平和客户的满意度。
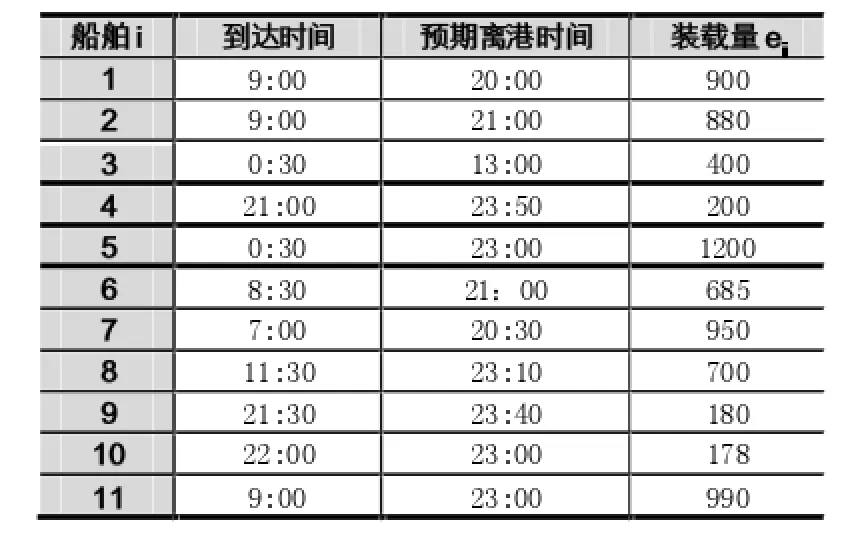
表3 到港船舶数据

表4 结果比较
5 结语
本文主要研究了在考虑船舶优先权的因素下,建立优化模型,以最小化船舶总的在港时间为目标函数,从而减少时间成本,并设计改进的遗传算法对算例进行求解,在遗传算法设计中,将泊位-岸桥集成分配转化为对泊位的岸桥分配以及船舶调度,从而减少了岸桥移动的成本。最后对比计算结果,证明了模型和算法是有效的,并且表明考虑到船舶优先服务权的模型更有利于提高码头的作业效率。但是在本文的泊位-岸桥分配中并未考虑到实际作业中的不确定因素的影响,所以可以在今后的研究中继续深化。
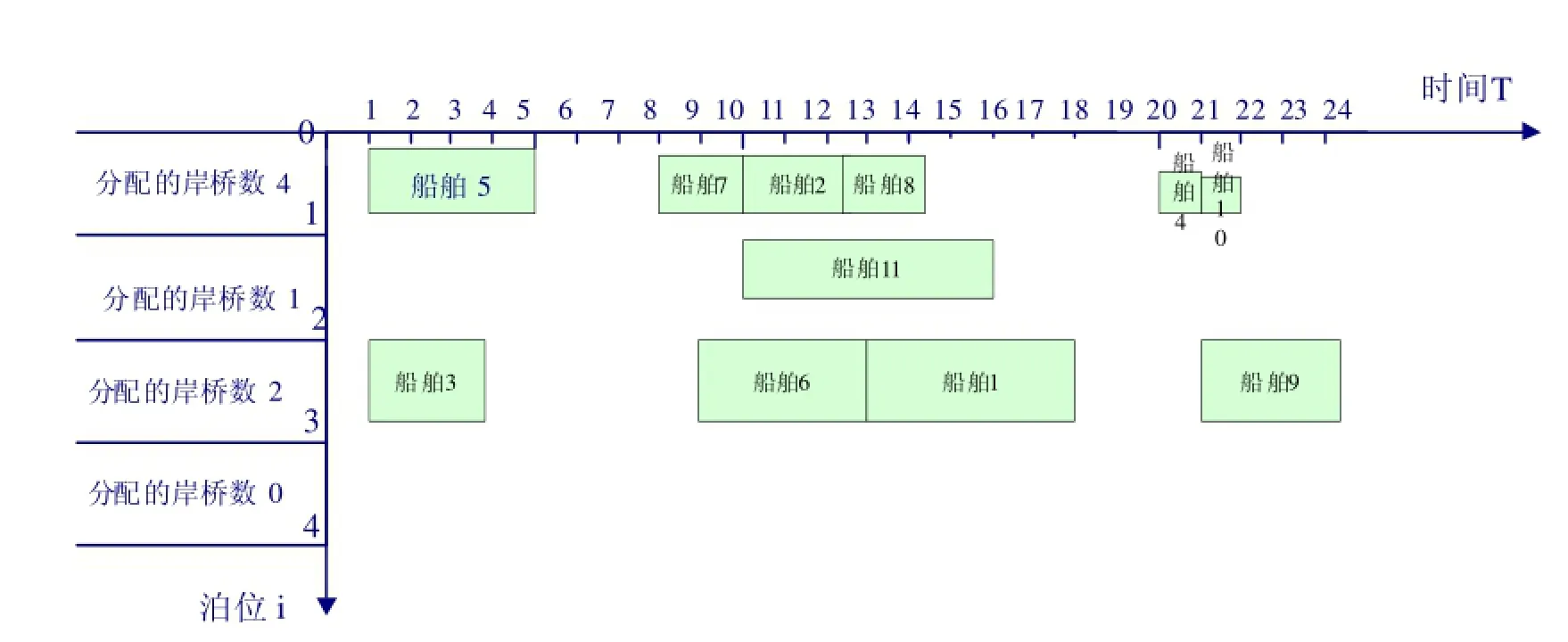
图5 σ=0时泊位-岸桥分配图
[1]Rashidi,H.,Dynamic Scheduling of Automated Guided Vehicles.Ph.D.Thesis,University of Essex,Colchester,2006
[2]Oguz,C.,B azewicz,J.,Cheng,T.C.E.,Machowiak,M.,Berth Allocation as Amoldable Task Scheduling Problem.In:Proceedings of Ninth International Workshop on Project Management and Scheduling,pp.201~205,2004
[3]Imai,A.,Chen,H.C.,Nishimura,E.,Papadimitriou,S..The Simultaneous Berth and Quay Crane Allocation Problem.Transportation Research Part E.2008,44(5):900~920
[4]Liang,C.,Huang,Y.,Yang,Y.,A Quay Crane Dynamic Scheduling Problem by Hybrid Evolutionary Algorithm for Berth Allocation Planning.Computers and Industrial Engineering,2008,56(3):1021~1028
[5]Meisel,F.,Seaside Operations Planning in Container Terminals.Physica,Berlin et al.2009
[6]Bierwirth,C.,Meisel,F.,2009.A Fast Heuristic for Quay Crane Scheduling with Interference Constraints.Journal of Scheduling,doi:10.1007/s10951-009-0105-0.
[7]杜玉泉,陈秋双,姬晓涛.面向服务的泊位和岸桥联合调度[J].计算机集成制造系统,2011,17(9):2051~2060
[8]赵坤强,韩晓龙,梁承姬.连续泊位下集装箱港口泊位与吊桥协同调度优化研究[J].武汉理工大学学报,2011(11):0060-06
[9]李娜,靳志宏.连续泊位调度与岸桥配置协同优化[J].中国航海,2011,34(2):86~90
[10]乐美龙,刘菲.基于Memetic算法的泊位和岸桥分配问题[J].武汉理工大学学报,2011,33(11):66~71
Berth-Quay Crane Allocation;Genetic Algorithm;Service Priority;Vessel Scheduling
Berth-Quay Crane Allocation Based on the Ships'Service Priority
ZHANG Di,YAN Nan-nan
(College of Information Engineering,Shanghai Maritime University,Shanghai 201306)
To solve the berth-quay crane allocation problem,formulates the mode with ships'service priority which aims to improve the service quality of container terminal and customers'satisfaction.And adopts the genetic algorithm with the heuristic algorithm for quay crane allocation for solving the problem,including the quay crane allocation and the corresponding vessel schedule in each berth.The results show that the algorithm is feasible and the turnaround time of vessels at port is less.In this connection,the efficiency of terminal operation is improved.
1007-1423(2015)14-0045-06
10.3969/j.issn.1007-1423.2015.14.011
张迪(1990-),女,安徽亳州人,硕士研究生,研究方向为港口物流优化
严南南(1968-),女,湖北鄂州人,博士,副教授,研究方向为智能信息处理与港口物流
2015-03-24
2015-05-12
