风电齿轮箱直齿轮传动系统动态特性影响分析

赵昕，陈长征，刘杰(沈阳工业大学机械工程学院，辽宁沈阳110870)

风电齿轮箱直齿轮传动系统动态特性影响分析

赵昕，陈长征，刘杰
(沈阳工业大学机械工程学院，辽宁沈阳110870)

综合考虑齿轮啮合刚度、齿侧间隙、齿轮啮合误差以及外部激励等多种非线性因素对齿轮传动系统动态特性的影响，建立风电齿轮箱传动系统高速级直齿轮传动的纯扭转非线性动力学模型，用拉格朗日方程推导了传动系统的振动微分方程。采用Runge－Kutta法对直齿轮系统非线性动力学模型进行求解，得到传动系统的时域波形、频谱图和相位图。定量给出齿轮转速、齿侧间隙等参数变化对齿轮传动系统动态特性的影响。结果表明:随着转速和齿侧间隙的增大，传动系统的振动幅值明显增大，系统的振动加剧。为风电齿轮箱传动系统的固有特性，动态响应等动力学特性奠定了一定的基础。

直齿轮;齿侧间隙;动态特性;内外激励

0　前言

随着能源和环境问题日趋严峻，风力发电在世界范围内得到快速发展，风力发电机作为风力发电系统的核心关键设备，其国产化设计制造问题成为风力发电的瓶颈。在风力发电机中，齿轮传动增速箱是一个关键部件，由于齿轮转速的提高和传递功率的增加，载荷工况越来越复杂，对齿轮传动性能也提出了更高的要求。而在实际使用中，风力发电机的故障50%左右发生在齿轮传动系统［1］。因此，研究各种随机工况条件下齿轮系统的动力学行为具有重要意义。

长期以来，国内外学者对齿轮系统的振动特性进行了大量的理论分析和试验研究［2-9］。Kahranman等［2-3］研究了各种不同形式激励下齿轮传动系统的动态响应。Parker等［4］分析了时变啮合刚度、摩擦因数、齿轮弯曲、重合度和模态阻尼等参数的变化对稳定性边界的影响。LIN等［5-7］利用不同方法建立了行星齿轮传动的扭转动力学模型，分析了行星齿轮的非线性动力学响应。陈思雨等［8］研究了轮齿随机间隙对齿轮系统动力学响应的影响。卢剑伟等［9］将间隙作为随机变量，利用分岔图和最大Lyapunov指数等对齿轮副系统的动力学形态进行了分析。当齿轮传动系统在高速运行时，用传统线性模型和线性理论己经不能真实可靠地反映系统的动力学行为［10-11］。随着振动理论不断完善，综合考虑多种非线性因素耦合，更能反映真实情况下系统的振动特性。

本文建立大型风力机齿轮箱高速级直齿轮传动系统纯扭转非线性动力学模型，用拉格朗日方程推导了传动系统的振动微分方程，并对其进行数值计算分析，研究了齿轮转速、齿侧间隙参数变化对齿轮传动系统动态特性的影响，为风电齿轮箱直齿轮传动系统的固有特性，动态响应等动力学特性奠定了一定的基础。

1　齿轮系统非线性动力学模型

假设齿轮系统的传动轴和支承轴承都是刚性的，忽略轮齿齿面间的滑动摩擦，建立如图1所示的一对齿轮副的动力学模型。

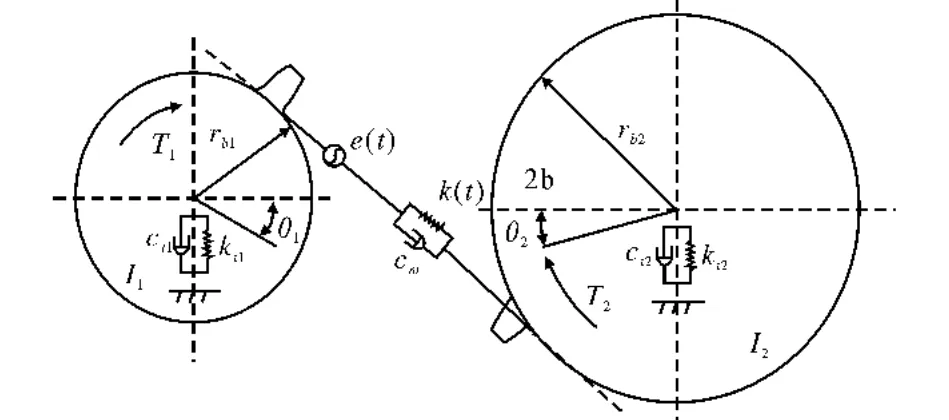
图1　齿轮副扭转振动分析模型Fig.1 Torsional vibration analysismodel of gear transmission system

根据拉格朗日方程推导齿轮系统的扭转振动方程:

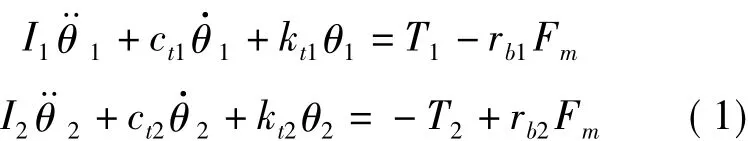
式中，I1、I2分别为主从动齿轮的转动惯量; rb1、rb2分别为主从动齿轮的基圆半径，两基圆的内公切线即为啮合线，用虚线表示;T1、T2分别为主从动齿轮的转动力矩;θ1、θ2分别为主从动齿轮的扭转振动位移;ct1、ct2分别为主从动齿轮的粘性阻尼系数;kt1、kt2分别为主从动齿轮的弹簧刚度;Fm为齿轮副动态啮合力，其表达式为

定义e(t)为轮齿的啮合误差，则

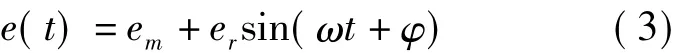
式中，em为齿轮啮合误差的常值;er为齿轮啮合误差的幅值;ω=2πn1z1/60，n1为主动齿轮转速，z1为主动齿轮的齿数;φ为初始相位角。

定义δ为轮齿动态传递误差，则两齿轮啮合线上的相对位移可以表示为

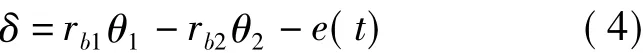
［12］单对齿轮副系统的间隙非线性函数可以表示为

式中，b为相对于刚度转折点的相对位移。将式(2)～(5)代入式(1)，可写

式中，cm为齿轮副的啮合阻尼系数;km为齿轮副的啮合刚度。

将式(6)进一步简化，写为矩阵形式

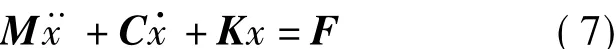
式中，M为系统质量矩阵，C为系统阻尼矩阵，K为时变刚度矩阵，均为2阶方阵，F为载荷列向量。

2　系统数值仿真

齿轮系统参数如下:直齿轮齿数Z1=25，Z2=98;齿轮模数m=8 mm;转动惯量I1=0.207 kg·m2，I2=44.355 kg·m2;半径rb1=0.1 m，rb2=0.4 m;扭转刚度kt1=0.254×106(N·m/ rad)，kt2=4.027×106(N·m/rad);阻尼系数ct1，ct2=5.0×102(N/rad/s);齿轮副的啮合阻尼系数cm=8.0×102(N/(m/s));齿轮副的啮合刚度km=6.0×106(N/m);齿轮啮合误差的常值em=2.0×10－5m;齿轮啮合误差的幅值er= 3.0×10－5m;齿轮副的转动力矩T1=100 N/m，T2=300 N/m。考虑齿侧间隙、啮合阻尼为非线性因素，用Runge-Kutta数值方法对上述公式进行求解，得到齿轮系统的时域波形、频谱响应和相位图。

2.1齿轮转速的影响

在实际齿轮传动系统中，转速常作为控制参数。对齿轮传动系统在不同转速工况下的系统振动响应进行计算。图2为主动齿轮转速取500 r/min、700 r/min、900 r/min时齿轮副的时域波形、频谱响应、相位图。图中ω=700 r/ min、ω=900 r/min时振动波形明显改变且振动位移幅值明显增大;图2a揭示了转频(fr=n1/ 60)及其倍频(nfr)等离散频率成分，图2b中只出现了明显的转频成分(fr)，其他谐波频率成分逐渐消失，转频幅值增大;图2c系统的相图没有明显的变化规律，系统逐渐处于稳定状态。根据图2可知，随着转速增大，系统扭转振动波形明显改变，扭转振动位移明显增大，转频幅值增大且成分单一，系统由非稳定状态趋于稳定状态。

图2　齿轮副的时域波形、频谱图、相位图Fig.2 Time domain waveform，spectrogram and phase graph of gear transmission system

2.2齿侧间隙的影响

齿侧间隙的存在会导致齿轮啮合时轮齿间接触、脱齿、再接触的重复冲击，表现出强烈的非线性，对齿轮系统振动特性产生重要影响。当齿面间隙变化时，从相图和振动幅值来分析系统的响应。图3为齿面间隙b取2×10－5m、3.2× 10－5m、6.4×10－5m时系统的时域波形、频谱图、相位图。b=2×10－5m时系统的谐波成分较为单一，b=3.2×10－5m、b=6.4×10－5m时振动位移幅值明显增大;图3a中只表现出了转频(fr=n1/60)成分、啮合频率(nfr)成分，并且啮合频率幅值大于转频成分的幅值，图3b中除了转频、啮合频率成分外还出现了倍频成分，图3c仅有1倍转频和啮合频率且1倍频幅值明显大于啮合频率幅值;图3a显示出近似椭圆运动轨迹，系统表现出稳定状态，图3b周期性变化不明显，图3c显示近似周期性运动轨迹。根据图3可知，随着齿侧间隙增大，振动位移、响应幅值均逐渐增大，系统处于低频状态，且由周期响应走向非周期，加剧了啮合冲击性。因此，选择齿侧间隙时，既要保证振动位移要小，又要保证振动周期性良好。

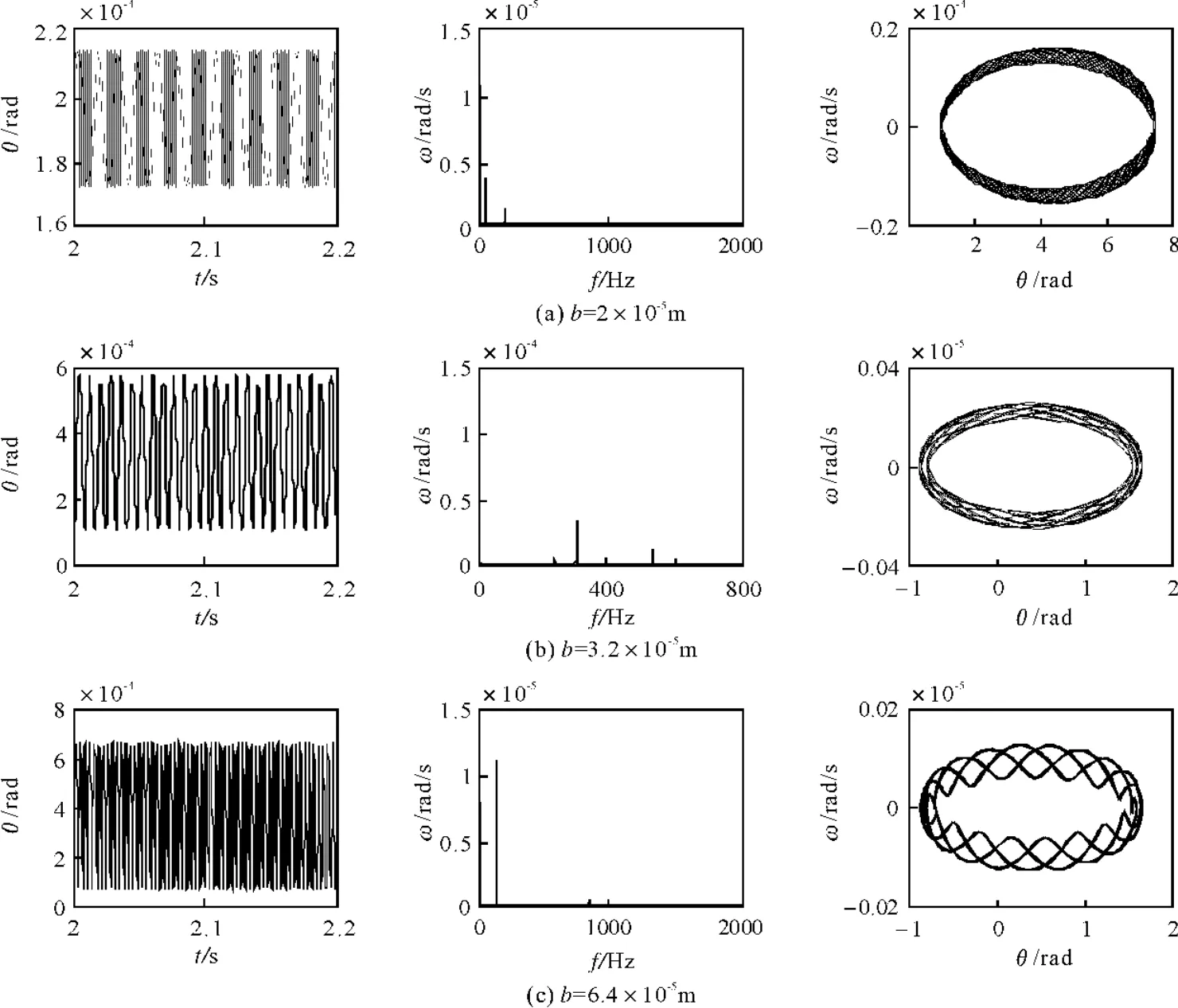
图3　齿轮副的时域波形、频谱图、相位图Fig.3 Time domain waveform，spectrogram and phase graph of gear transmission system

3　结论

本文建立了大型风力机齿轮箱传动系统高速级直齿轮传动的纯扭转非线性动力学模型，应用拉格朗日方程推导了传动系统的振动微分方程，通过改变齿轮不同转速、齿侧间隙参数值，采用数值方法，对比分析齿轮传动系统非线性振动特征及系统振动响应规律。结果表明，随着转速和齿侧间隙的增大，传动系统的响应幅值明显增大，传动系统的振动加剧。为风电齿轮箱传动系统的固有特性，动态响应等动力学特性奠定了一定的基础。

参考文献:

［1］秦大同，邢子坤，王建宏，等．基于动力学的风力发电齿轮传动系统可靠性评估［J］．重庆大学学报:自然科学版，2008，30(12):1－6．

［2］Kahraman A，Singh R．Non-linear dynamics of a spur gear pair［J］．Journal of sound and vibration，1990，142(1):49－75．

［3］Kahraman A，Singh R．Non-linear dynamics of a geared rotor-bearing system withmultiple clearances［J］．Journal of Sound and Vibration，2013，144(3):469－506．

［4］Liu G，Parker R G．Impact of tooth friction and its bending effecton gear dynamics［J］．Journalof Sound and Vibration，2009，320(4):1039－1063．

［5］Lin J，Parker R G．Analytical characterization of the unique properties of planetary gear free vibration［J］．Journal of Vibration and Acoustics，1999，121(3): 316－321．

［6］Lin J，Parker R G．Planetary gear parametric instability caused by mesh stiffness variation［J］．Journal of Sound and vibration，2002，249(1):129－145．

［7］Parker R G，Agashe V，Vijayakar SM．Dynamic response of a planetary gear system using a finite element/contactmechanics model［J］．Journal of Mechanical Design，2000，122(3):304－310．

［8］陈思雨，唐进元．间隙对含摩擦和时变刚度的齿轮系统动力学响应的影响［J］．机械工程学报，2009，45(8):119－124．

［9］卢剑伟，曾凡灵，杨汉生，等．随机装配侧隙对齿轮系统动力学特性的影响分析［J］．机械工程学报，2010(21):82－86．

［10］王立华，李润方，林腾蛟，等．齿轮系统时变刚度和间隙非线性振动特性研究［J］．中国机械工程，2003，14(13):1143－1146．

［11］杨振，王三民，范叶森，等．正交面齿轮传动系统非线性振动特性研究［J］．振动与冲击，2010，29 (9):218－221．

［12］Lin Tengjiao，Wang Danhua，Ran Xiongtao et．al．Coupled nonlinear vibration analysis of multi-stage gear transmission system［J］．Journalof vibration and shock，2013，32(17):1－8．

Dynam ic characteristics of spur gear transm ission system for w ind turbine

ZHAO Xin，CHEN Chang-zheng，LIU Jie
(School of Mechanical Engineering，Shenyang University of Technology，Shenyang 110870，China)

A nonlinear dynamic model of spur gear transmission system is builtwith consideration of gearmesh stiffness，backlash，error of tooth mesh and external excitation．The vibration differential equations of transmission system are derived by Lagrange equation．Time domain waveform，spectrogram and phase graph of gear transmission system are obtained by Runge-Kuttamethod．It is studied thatparametric variation such as rotating speed and backlashes is influence on dynamic characteristic gear transmission system．The result shows that vibration amplitude of gear transmission system is lager and vibration is more serious with the increase of rotational speed and backlash．The conclusions lay the certain foundation for natural characteristics and dynamic response of spur gear transmission system．

spur gear;backlash;dynamic characteristics;internal and external excitation

TH113

A

1001－196X(2015)02－0022－04

2014－11－27;

2014－12－08

国家青年科学基金项目(51305276)

赵昕(1988－)，女，沈阳工业大学机械工程学院博士研究生。