含间隙同步锥齿轮锁定后的非光滑动力学分析*
2015-11-25李春洋张伟
李春洋张伟
(北京工业大学机械工程与应用电子技术学院,北京 100124)
含间隙同步锥齿轮锁定后的非光滑动力学分析*
李春洋†张伟
(北京工业大学机械工程与应用电子技术学院,北京 100124)
针对周边环形桁架天线展开锁死后,分析齿轮副间隙由于空间冷—热环境交替对天线所产生的影响.因为整个桁架结构复杂,间隙种类众多,所以文中只研究一对同步直齿锥齿轮锁定后间隙的非光滑动力学行为.文中首先介绍了三种碰撞力模型,即恢复系数模型、Hertz接触力模型和非线性弹簧—阻尼模型,然后对物理模型进行简化得到动力学模型,最后建立了动力学方程.由于动力学方程中存在分段,直接求得解析解难度过大,文中直接采用数值仿真的方法进行分析,从仿真结果中得知含间隙的同步锥齿轮在外力的作用下整个系统会出现单倍周期、倍周期分岔和混沌等复杂的非线性响应.
间隙,碰撞,周期分岔,混沌响应
引言
同步锥齿轮传动中,由于制造和安装时出现的误差及使用过程中产生的磨损,都不可避免地导致齿轮的轮齿之间间隙的出现,由于齿轮中的轮齿、润滑油等在太空由于太空环境温度的不断交替而产生能量损耗,对含间隙的同步齿轮的一对轮齿与润滑油之间将发生接触—碰撞—分离的往复运动.对进行动力学分析和齿轮系统的间隙碰撞[1-2]振动研究有着十分重要的意义.碰撞系统建模的方法主要有以下四种:恢复系数法、圣维南法、非线性有限元法和弹簧—阻尼模型,其中恢复系数法和弹簧—阻尼模型在碰撞振动动力学研究中应用最为广泛.恢复系数法[3-6]假设接触碰撞过程是瞬间完成的,且碰撞体的外形没有根本的改变,即忽略了接触时间和接触变形,只关心和研究碰撞前与碰撞后的动力学形态,而用恢复系数来表示碰撞前后速度的跳跃关系.非线性弹簧一阻尼模型能够比较精确地反映碰撞过程中的变形能量损耗,Zhang和sharf[7]通过实验证明了在弹性碰撞情况下非线性弹簧—阻尼模型的合理性和实用性.齿轮的冲击系统模型最早是由Dubowshy和reudenstein[8-9]在1971年提出的,但是研究轮齿冲击动力学行为时将冲击接触过程简单地用粘性阻尼来表示,并不能真实的反映齿轮冲击特性.Hunt和Crossley[10]等通过引入非线性冲击阻尼的概念来建立了含有冲击阻尼的冲击系统动力学模型.Veluswami和Crossley[11]利用这种冲击模型分析了两边约束的球振动模型,理论分析得到的结果与试验基本吻合,证明了冲击阻尼模型在研究冲击动力学的有效性.1984年,Pfeiffer[12]在研究齿轮传动系统动力学时建立了一种冲击模型,随后在文章中应用理论分析和实验方法,揭示了齿轮系统的常规运动和混沌运动状态.在2005年,Luo和Chen[13-16]建立了一类比较简单的分段线性冲击系统的理论模型,应用解析法分析了系统的周期运动,应用局部奇异性理论分析其周期解的擦边分岔,以及应用数值法模拟其混沌过程,此后又中讨论了此类系统的奇怪吸引子的擦边分岔,之后应用映射结构技术解析分析此类系统的任意周期运动.就现有文献来看,针对对齿轮传动系统的间隙和时变啮合刚度的非线性问题已进行了大量的研究,分别建立了单自由度[17-21]、三自由度[22]间隙非线性动力学模型,考虑周期时变刚度[20-21,23]的影响,并用各种方法研究齿轮系统的周期运动、混沌响应及分岔[22-23],两自由度间隙非线性动力学模型比较少.另外针对含间隙同步锥齿轮锁定后的非光滑动力学分析相对较少.文中建立了一种含间隙的两自由度齿轮传动系统的动力学模型.通过数值仿真对齿轮传动系统的分岔和混沌等非线性动力学行为进行分析研究,对以后更好的完善含间隙和润滑的齿轮副运动副模型奠定了基础.
1 接触碰撞模型
1.1 恢复系数
在机械结构中碰撞过程往往不是完全弹性碰撞,也不是完全非弹性碰撞,也导致碰撞过程总会存在着一定的能量损失,而这一部分损失的能量可以用恢复系数来表达.假设碰撞前两质体的速度为υ1i、υ2i,碰撞后的速度为υ1j、υ2j,则恢复系数可由下式表示,
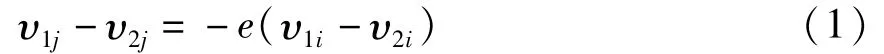
并且有0≤e≤1,对于完全弹性碰撞e=1,对于完全非弹性碰撞e=0.恢复系数的大小跟很多因素有关,如接触面的几何形状,碰撞速度,材料属性,接触持续的时间,甚至摩擦.当碰撞持续时间与碰撞体基本固有振动模的周期之比很大时,恢复系数的大小便决定于碰撞点附近的塑性变形量,而碰撞点附近的塑性变形主要由碰撞速度决定.
1.2 Hertz接触力模型
Hertz接触力模型是基于完全弹性变形,主要研究了弹性体的准静态接触问题,并且该模型是非线性接触力模型,但是没有考虑到接触的过程中能量的损耗.Hertz接触力模型可以用一个非线性弹簧来描述,其接触力公式为,

其中,δ为接触面的变形量,n是与接触面几何特征有关的常数,一般取1.5,K是与质体材料特性和结构参数有关的常数,

式中,Ri和Rj表示正面碰撞质体的球面半径,σi和σj表示如下,

νh和Eh分别表示两个质体的泊松比和杨氏模量.
1.3 非线性弹簧—阻尼模型
当质体发生碰撞时,碰撞面之间发生弹性变形,从而产生接触碰撞力,碰撞力的大小与变形量有关,根据上一节Hertz理论的相关描述可知.
变形恢复后速度的大小不能恢复到碰撞前的速度的大小,因为在碰撞过程中伴随着能量损耗,用于产生变形和热,而上面的碰撞力模型不能反映能量损耗的实际情况.因此在碰撞力模型中必须引入阻尼系数D,将碰撞力表示,

其中,˙δ为相对速度,阻尼系数D采用迟滞阻尼模型,

μ是迟滞阻尼系数,μ的值与粘性阻尼系数、剪切和体积变形等有关,通过能量法可以得到μ的表达式,

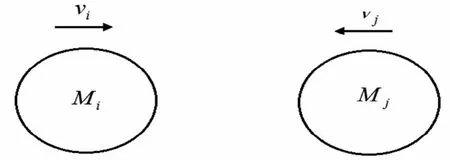
图1 质体正碰示意图Fig.1 Plastid schematic with frontal collision
因此,碰撞力的表达式为,
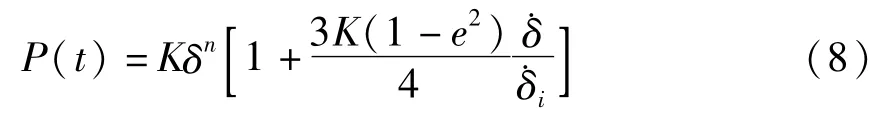
2 直齿锥齿轮力学模型
2.1 物理模型简化
同步直齿锥齿轮副锁死后如图2,物理模型可简化为含参数激励且具有含间隙的两自由度齿轮在外激励作用下的动力学模型.

图2 间隙大小为B同步锥齿轮物理模型Fig.2 Gap size is B physical model of the synchronous straight bevel gears
如图3所示,M1和M2分别是主动轮齿和被动轮齿的广义等效质量,K1和K2分别是主动轮齿和被动轮齿的接触刚度,间隙B表示M1和M2的齿侧间隙,而齿轮中的润滑油等在太空由于冷热冲击的不断交替而产生能量损耗,在此简化为模型中的阻尼部分C1、C2和激励力F(t)(QsinΦt),Q和Φ分别表示冷热冲击的激励的幅值和频率.假设轮齿为弹性体,在激励力作用下,则轮齿间发生接触—碰撞—分离的往复运动(由于对模型简化的需要,模型并未考虑齿轮接触面的摩擦).
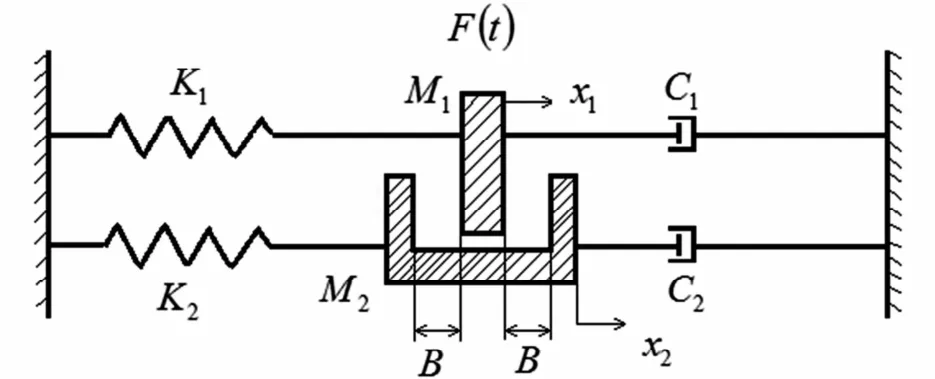
图3 两自由度齿轮碰撞力学模型Fig.3 Two degrees of freedom about gear collision dynamics model
2.2 动力学模型的建立
当M1与M2之间的相对位移时,M1与M2不发生接触;当M1与M2之间的相对位移x1-x2=B时,M1与M2刚发生接触,并没有力的作用,因此,M1和M2分别做自由振动,其振动系统的运动微分方程为
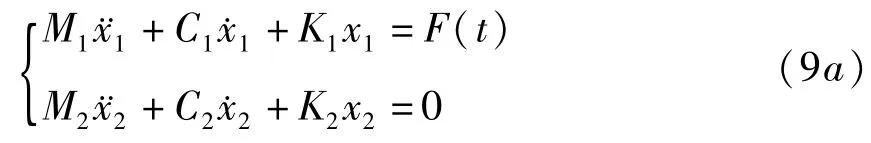
当M1与M2之间的相对位移x1-x2<-B和x1-x2>B时,M1与M2将发生接触,此时相对速度不等于0,接触面上将产生弹性碰撞,两质量体分别发生压缩弹性变形直到质量块的速度为0,然后恢复弹性变形,直至质量体分离.碰撞过程的运动微分方程可表示为
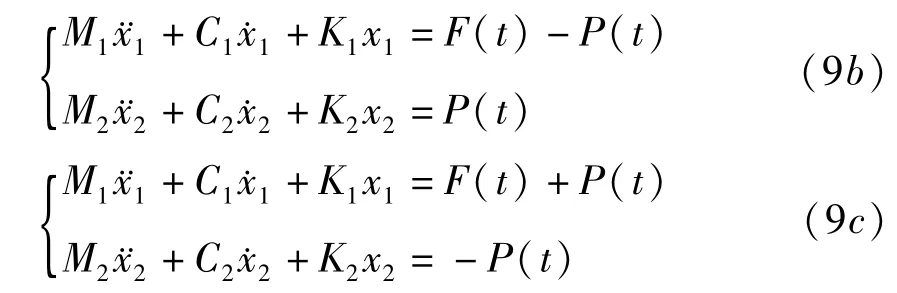
式中,P(t)的表达式如公式(8)所示.显然,当x1-x2>B时,M1与M2的右侧面发生接触碰撞,当x1-x2<B时,M1与M2的左侧面发生接触碰撞.为了方便地应用数值积分法求解此动力学问题,需要对方程进行无量纲化.取无量纲量,τ=ω1t,ωi=得到三组无量纲方程为,

3 数值分析
碰撞系统参数的变化,将使系统呈现出复杂的非线性动力学现象,如混沌、分岔等.
在图3中所示的动力学模型中,首先将系统参数B=0.1,ζ1=ζ2=0.2,η=1,κ=20,λ=3.5,n=1.5,g=2代入(10.1)、(10.2)、(10.3)中,取ω为控制参数.从图2中可知,随着ω的变化,此系统中x1呈现出周期运动与混沌的交替,即:单倍周期运动-二倍周期运动-倍周期-二倍周期运动-混沌运动.

图4 系统在ω为控制参数时的分岔图Fig.4 System in the control parameter of ω bifurcation diagram
以下均为固定初始条件和其他参数的大小,增大转速ω所得的系统运动情况.
当ω=0.5时,系统出现单倍周期运动.系统的平面相图,三维相图,波形图如图5所示.
当ω=0.8时,系统出现单倍周期运动.系统的平面相图,三维相图,波形图如图6所示.

图5 ω=0.5时系统进行单倍周期运动Fig.5 Single-periodic motion
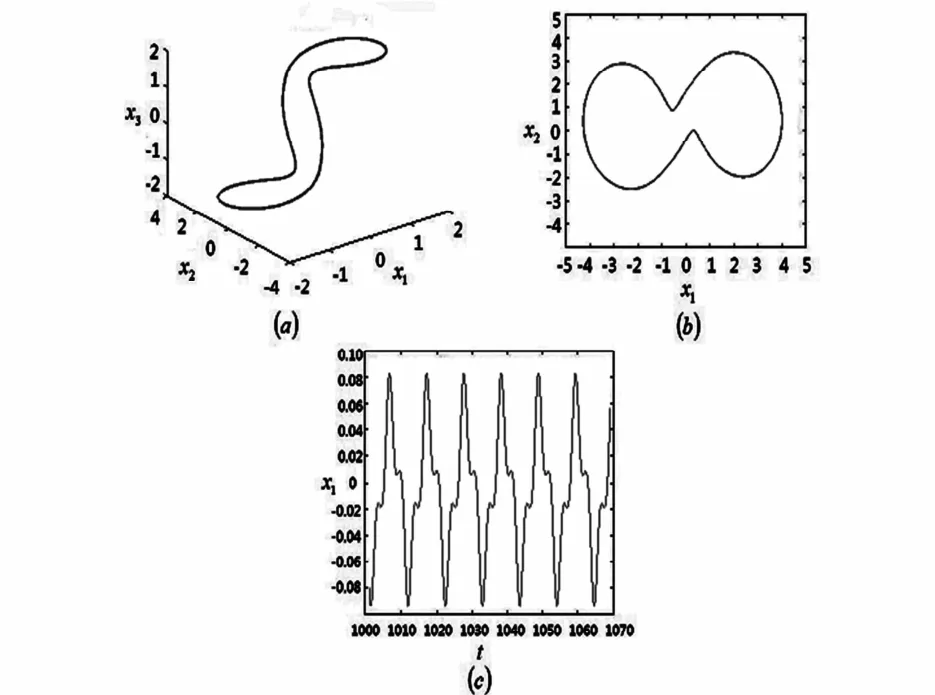
图6 ω=0.8时系统进行单倍周期运动Fig.6 Single-periodic motion
当ω=1.3时,系统出现概周期运动.系统的平面相图,三维相图,波形图如图7所示.
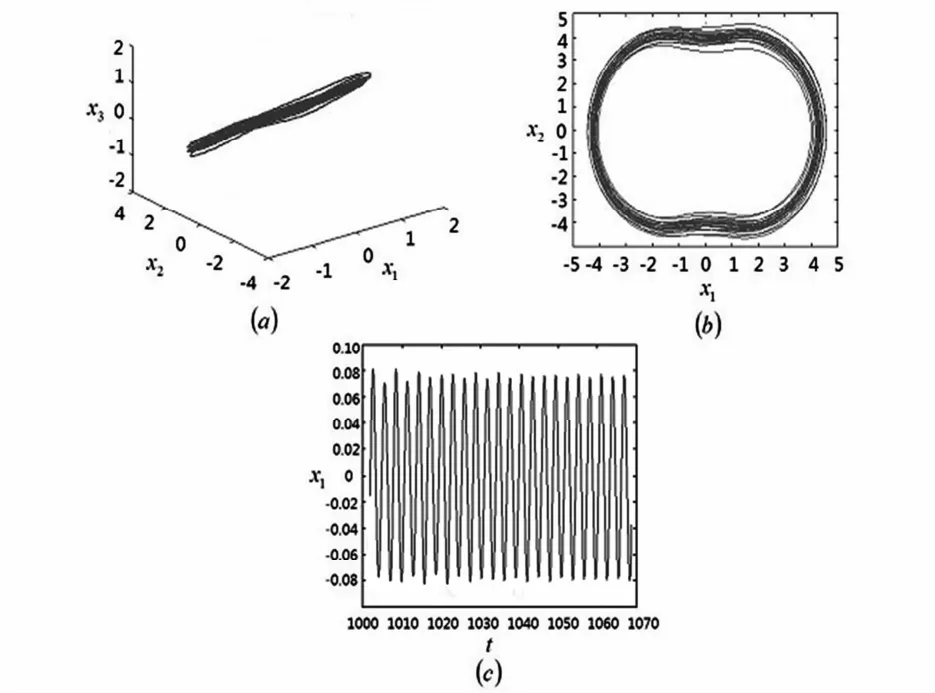
图7 ω=1.3时系统进行概周期运动Fig.7 Quasi-periodic motion
当ω=2.0时,系统出现二倍周期运动.系统的平面相图,三维相图,波形图如图8所示.
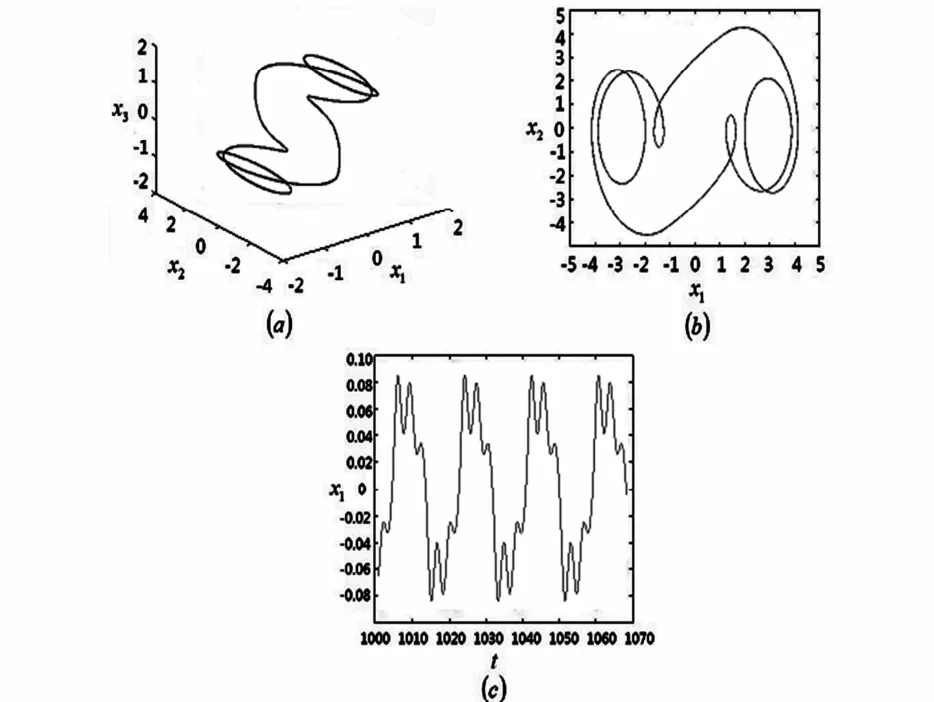
图8 ω=2.0时系统出现二倍周期运动Fig.8 Two-periodic motion
当ω=2.35时,系统出现多倍周期运动.系统的平面相图,三维相图,波形图如图9所示.
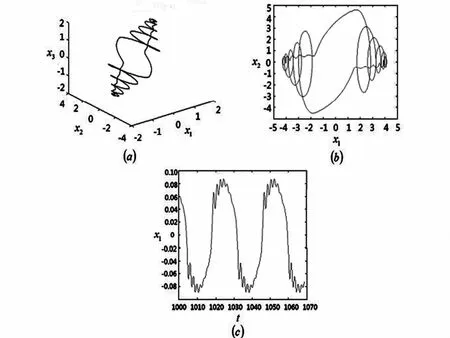
图9 ω=2.35时系统多倍周期运动Fig.9 There-periodic motion
当ω=2.4时,系统出现概周期运动.系统的平面相图,三维相图,波形图如图10所示.
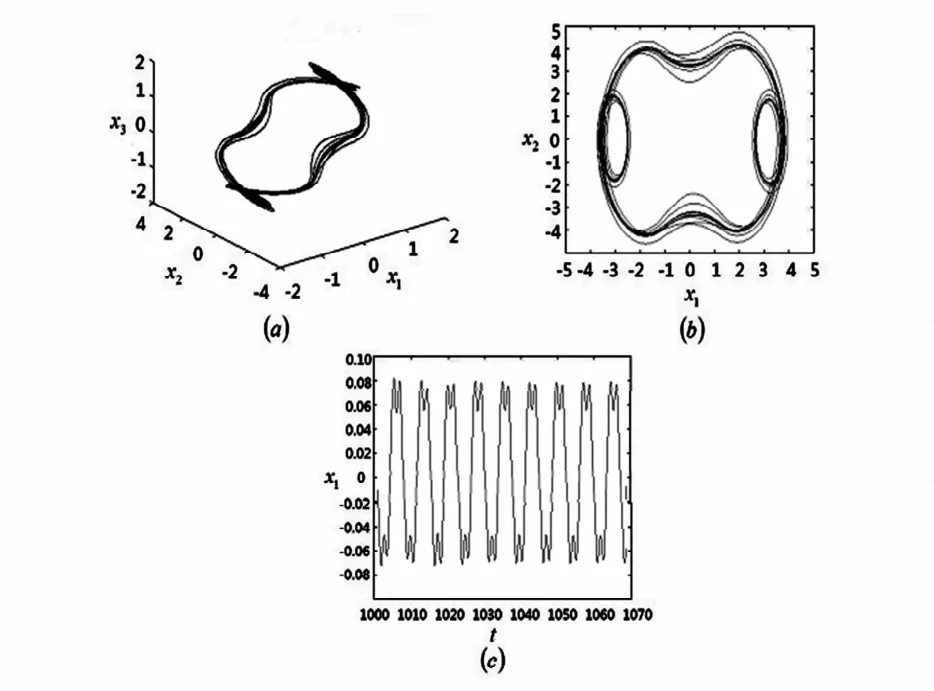
图10 ω=2.4时系统出现概周期运动Fig.10 Quasi-periodic motion
当ω=2.8时,系统出现混沌运动.系统的平面相图,三维相图,波形图如图11所示.
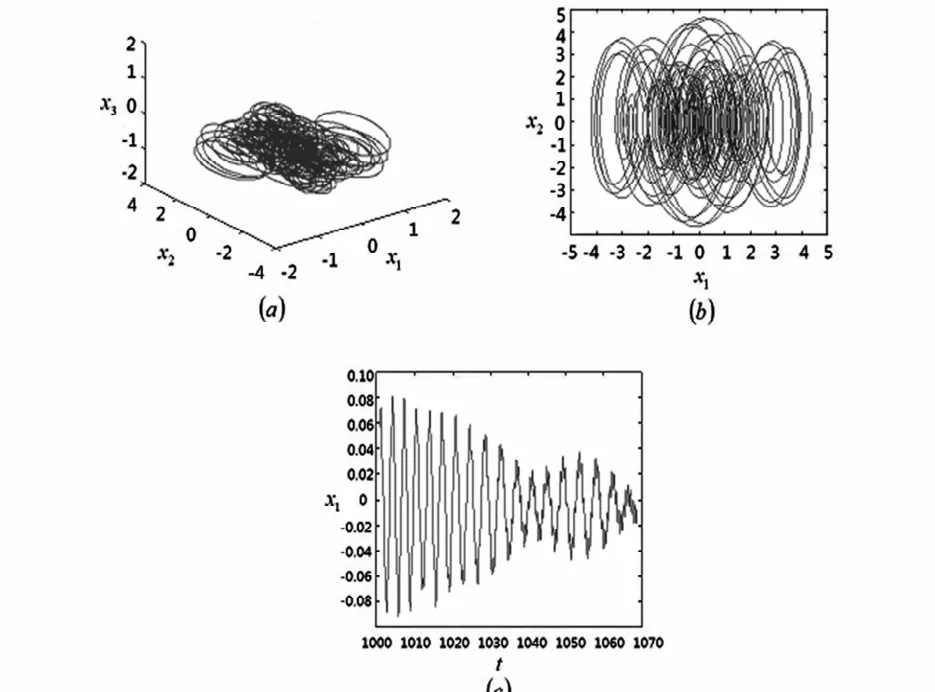
图11 ω=2.8时系统出现混沌运动Fig.11 Chaotic
4 结论
⑴含间隙同步锥齿轮在锁定后,系统由于受到外部环境温度的影响,系统中将会出现着周期运动、混动运动等现象.系统依次经历单倍周期,分岔为两倍周期,之后分岔为多倍周期;随着外激励的变化,多倍周期又回到两倍周期,最后系统再次进入混沌.
⑵通过分析齿轮锁死后间隙结构出现的几种形式的非线性动力学现象,对于通过选择合适的系统参数来减小甚至消除这种颤振有一定的参考意义.
1 李万祥,牛卫中.一类含间隙系统的分岔与混沌的形成过程.振动与冲击,2005,24(3):47~49(Li W X,Niu W Z.Bifurcation and chaos of a system with a pair of symmetric set up elastic stops.Journal of Vibration and Shock,2005,24(3):47~49(in Chinese))
2 马永靖,丁旺才,杨小刚.碰撞振动系统的参数自调节混沌控制.振动与冲击,2007,26(1):24~26(Ma Y J,Ding W C,Yang X G.Chaos control of a vibro-impact system with parameter adjustment.Journal of Vibration and Shock,2007,26(1):24~26(in Chinese))
3 罗冠炜,谢建华.两自由度塑性碰撞振动系统的动力学研究.力学学报,2000,32(5):579~586(Luo G W,Xie J H.Dynamic of a two-degree-of-freedom vibration system with perfectly plastic impacts.Acta Mechanica Sinica.2000,32(5):579~586(in Chinese))
4 罗冠炜,谢建华.一类含间隙振动系统的周期运动稳定性、分岔与混沌形成过程研究.固体力学学报,2003,24(3):284~292(Luo G W,Xie J H.Researches on stability of periodic motion,bifurcations and chaos in a vibratory system with a clearance or gap.Acta Mechanica Solida Sinica,2003,24(3):284~292(in Chinese))
5 皇甫玉高,李群宏.一类单侧碰撞悬臂振动系统的擦边分岔分析.力学学报,2008,40(6):812~819(Huang PU Y G,Li Q H.Grazing bifurcation of a vibrating cantilever system with one-sided impact.Acta Mechanica Sinica,2008,40(6):812~819(in Chinese))
6 张有强,丁旺刁.干摩擦对碰撞振动系统周期运动的影响分析.振动与冲击,2009,28(6):110~112(Zhang Y Q,Ding W D.Dry friction vibration system periodic motion collision impact analysis.Journal of Vibration and Shock,2009,28(6):110~112(in Chinese))
7 Zhang Y,Sharf I.Validation of nonlinear viscoelastie contact force models for low speed impact.Journal of Applied Mechanics,2009,76(5):051002~12
8 Dubowsky S,Freudenstein F.Dynamics analysis of mechanical systems with clearances,part 1:formulation of dynamic model.ASME Translations,Journal of Engineering for Industry,1971,93(7):305~309
9 Dubowsky S,Freudenstein F.Dynamics analysis of mechanical systems with clearances,part 2:dynamic response.ASME Transactions,Journal of Engineering for Industry,1971,93(4):310~313
10 Veluswami M A,Crossley F R E.Multiple impacts of a ball between tow plates part 1:Some experimental observations.ASME Journal of Engineering for Industry,1975,97(6):820~827
11 Veluswami M A,Crossley F R E.Multiple impacts of a ball between tow plates part 2:mathematieal modeling.ASME Journal of Engineering for Industry,1975,97(6):828~835
12 KaragianLnis K,Pfeiffer F.Theoretical and experimental investigations of gear BOX.Nonlinear Dynamies,1991(2):367~387
13 Luo A C J,Chen L.Periodic motions and grazing in a harmonically forced,piecewise,linear oscillator with impacts.Chaos,Solitons&Fraetals,2005,24(8):567~578
14 Luo A C J.A theory for non-smooth dynamic systems on the connectable domains.Communications in Nonlinear Science and Numerical Simulation,2005,10(8):1~55
15 Luo A C J,Chen L D.The grazing mechanism of thestrange attractor fragmentation of a harmonically forced,piecewise,linear oscillator with impacts.Proceedings of the Institution of Mechanical Engineers,Part K:Journal of Multi-bodyDynamies,2006,220(2):35~51
16 Luo A C J,Chen L D.Arbitrary periodic motions and grazing switching of a force piecewise-linear,impacting oscillator.Journal of Vibration and Acoustics,2007,129(9):276~285
17 Kahraman A,Singh R.Non-linear dynamics of a spur gear pair.Journal of Sound and Vibration,1990,142(1):49~75
18 Blankenship G W,Kahraman A.Steady state forced response of a mechanical oscillator with combined parametric excitation and clearance type non-linearity.Journal of Sound and Vibration,1995,185(5):743~765
19 Raghothama A,Narayanan S.Bifurcation and chaos in geared rotor bearing system by incremental harmonic balance method.Journal of Sound and Vibration,1999,226(3):469~492
20 王三民,沈允文,董海军.含摩擦和间隙直齿轮副的混沌与分叉研究.机械工程学报,2002,38(9):8~11(Wang S M,Shen Y W,Dong H J.Chaos and bifurcation analysis of a spur gear pair with combined friction and clearance.Chinese Journal of Mechanical Engineering,2002,38(9):8~11(in Chinese))
21 王立华,李润方等.齿轮系统时变刚度和间隙非线性振动特性研究.中国机械工程,2003,14(13):1143~1146(Wang L H,Li R F et al.Research on nonlinear vibration characteristics due to time-varying mesh stiffness and gear backlash in gear system.Chinese Journal of Mechanical Engineering,2003,14(13):1143~1146(in Chinese))
22 刘晓宁.三自由度齿轮传动系统的非线性振动及混沌控制[硕士学位论文].西安:西北工业大学,2003(Liu X Y.Nonlinear oscillations and chaos control for three-degree-of-freedom gear transmission system[Master Thesis].Xi′an:Northwestern Polytechnical University,2003(in Chinese))
23 郜志英,沈允文,董海军等.齿轮系统倍周期分岔和混沌层次结构的研究.机械工程学报,2005,41(4):44~48(Gao Z Y,Shen Y W and so on.Research on perioddoubling bifurcation and chaos hierarchy in gear system.Chinese Journal of Mechanical Engineering,2005,41(4):44~48(in Chinese))
Received 21 March 2014,revised 20 April 2014.
*The project supported by the National Natural Science Foundation of China(11290152,11272008)
†Corresponding author E-mail:yangchunli1988@126.com
KINETIC ANALYSIS OF NON-SMOOTHAFTER THE SYNCHRONOUS STRAIGHT BEVEL GEARS WITH CLEARANCE BEING LOCKED*
Li Chunyang†Zhang Wei
(College of Mechanical Engineering and Applied Electronics Technology,Beijing University of Technology,Beijing 100124,China)
This paper focuses on the influence of joint clearance on the satellite dashes when the space environment alternates between cool and hot.Since the whole truss structure is complex and has many kinds of clearance,this paper only studied the nonlinear dynamical behavior of synchronous straight bevel gears which have clearance after the synchronous straight bevel gears is locked.The first model is Hertz contact force model;the second one is coefficient of restitution model;the last one is nonlinear spring-damping model.Then the physical model was simplified,the dynamic one was obtained,and the dynamic equation with the nonlinear spring-damping model was established.Due to the existence of segmentation in the dynamic equations,direct solve analytically is difficult,so this paper used numerical simulation method to analyze the model.From the analysis,it is obtained that the system of synchronous straight bevel gears with clearance will appear complex nonlinear phenomena such as Single-periodic,period-doubling bifurcation and chaotic responses.
clearance,collision,period-doubling bifurcation,chaotic responses
10.6052/1672-6553-2015-029
2014-03-21收到第1稿,2014-04-20收到修改稿.
*国家自然科学基金资助项目(11290152、11272008)
†通讯作者E-mail:yangchunli1988@126.com
