C-D 生产函数视域下的研发效率测度
——来自2000—2013年的宏观证据
2015-09-17云南大学会计学院云南昆明650091
(云南大学会计学院 云南昆明650091)
一、引言
科技是国家强盛之举,创新是民族进步之魂。纵观近百年来的世界产业发展史可知,科技创新是提高社会生产力和提升综合国力的战略支撑。企业是技术创新的主体,如何增强企业的创新能力,是各国创新政策的焦点和关键。根据国家统计局的数据显示,2012年我国高新技术企业共有24 636家,较2011年同比增长了13.6%;利润额高达6 186.34亿元,同比增长了18%;高新技术产业出口交货值46 701.09亿元,同比增加了15%;专利申请数为97 200件,同比增长了25%。高新技术企业强劲发展的一个重要因素是政府财政和企业自身的科技投入。2012年基于大中型工业企业口径下的高新技术产业,研究与试验发展经费为1 491.49亿元,同比增长了20.5%;科研人员的数量达52.6万人,同比增长了23%。我国研发费用支出R&D占GDP的比重不断攀升,从2000年的0.9%增长到2010年的1.75%,但与世界领先国家R&D占GDP比重平均为3%左右相比,差距仍然较大。显然,廉价的劳动力优势不能支撑我国经济的持续发展,转变发展方式是必然选择。转变发展方式的重要途径之一是加大研发投入,从而提高我国企业的核心竞争力。
二、文献回顾与假设提出
(一)国外研究动态。研发活动对企业收入以及企业发展有着积极的影响。 Leo Sveikuauskas(2001)考虑了研发投入的溢出效应和政府与企业双重投入的影响,得出了政府与企业的双重增长的结论。Bart Verspagen(1995)将企业分为高科技行业、中等技术行业和低技术行业,并认为高科技行业研发投入产出高,中等技术行业研发投入产出次之,低技术行业研发投入产出最差,说明不同行业的研发效率是 有 差 异 的 。 Bronwyn H.Hall、Zvi Griliches、Jerry A.(1986) 把专利看作研发产出,得出研发费用和专利有着很强的相关关系,并且这种关系不受企业规模的影响。事实上,研发投入与产出的过程或者机理极为复杂。纵观国外研究,学者们通过构建不同的模型来测算研发投入产出效率,大部分学者认为,投入与产出有着直接或间接的正相关关系,也有学者认为,研发投入与产出的关系非常复杂,应该更多地考虑影响研发投入或产出的因素,不能笼统地认为研发投入对产出有着积极的影响,研发投入与产出之间并非简单的关系。
(二)国内研究动态。在国外研究的基础上,国内关于研发支出的探讨也如火如荼地展开了。从总体上来看,我国研发投入力度显著低于西方发达国家水平,并且研发水平较低。霍静波(2012)认为,研发投入对研发产出有着积极的影响。吴延兵(2009)通过使用中国面板数据,实证研究了企业规模、产权结构等因素对研发投入与产出的影响,认为企业销售收入对研发投入有显著的正向影响,国有产权对研发投入没有显著影响。周群芳、吴婕、谷俊(2013)从专利引证的角度出发,发现因行业区别而造成的影响力差异较为明显,企业性质、研发政策对企业的影响力产生了一定的影响。孟庆军、许莲艳(2015)引入柯布-道格拉斯函数,发现科技投入会促进高新技术产业的发展及盈利能力的提高,但是,从长期看,这种水平的提高有一定的滞后期,这种滞后期使得科技投入对高新技术行业的促进作用并不明显。由于高新技术产品更新换代快、高新技术企业竞争激烈或者高新技术企业无法准确把握市场动向,高科技人才缺乏创新能力。
综上,学者们侧重于收入、研发投入等知识生产要素的贡献,也有对企业营业活动之外的环境因素的考量,发现我国企业的研发投入对研发产出有着积极的影响。但是,研发投入与产出的过程包含了很多其他干扰因素,选择合适的指标对研发投入和产出过程进行研究成为当务之急。
(三)研究假设。
纵观国内外文献,企业的研发活动过程涉及的变量较多,研发投入与产出的过程也很复杂。胡永平(2006)认为企业的产出与其物质资源的投入量有关,积极的经费投入会使企业积极开展研发投入与产出活动,也有利于产出结果市场化并提高收入。李正卫等(2014)认为,企业经费投入与研发能力正相关,而研发能力与企业销售收入正相关。据此本文提出假设1。
H1:在其他条件不变的情况下,新产品研发经费支出与新产品销售收入正相关。
Luthans(2005)认为,企业的人力资本是企业研发投入和产出活动中的关键流程,企业的人力资本能够通过有针对性的投入和开发而使研发产出成果更便利地实现市场化,并且得出人力资本投入与研发产出正相关的结论。研发人力资本对企业研发投入与产出活动至关重要,企业研发人员的乐观与否也对企业研发的投入和产出活动有着显著的影响。研发人员越多,企业的研发活动过程可能就会更顺利,新的研发成果就越有可能呈现出来,这样就会提高新产品的产量,进而提高新产品的销售收入。本文提出假设2。
H2:在其他条件不变的情况下,研发人员全时当量与新产品销售收入正相关。
Bronwyn H.Hall、Zvi Griliches、Jerry A.(1986)把专利看作研发产出,研发费用和专利有着很强的相关关系,这种关系不受企业规模的影响。杨虹(2014)认为,在企业研发的投入与产出活动中,专利在不同行业发挥的作用具有差异,在高科技行业的研发投入与产出活动中,有效专利对企业研发的投入与产出具有显著的影响,其他行业并不显著。有效专利数可能对新产品销售收入有着积极的影响,因为企业根据自身需要研发获得的专利,可以刺激企业继续研发,使得企业的研发活动更加高效。本文提出假设3。
H3:在其他条件不变的情况下,有效专利数与新产品销售收入正相关。
三、模型设定与指标选取
(一)柯布-道格拉斯(Cubb-Douglas)生产函数的背景。Cubb-Douglas生产函数由美国经济学家柯布(C.W.Cobb)和道格拉斯(P.H.Douglas)于1928年提出。道格拉斯 (1928)指出,Cubb-Douglas生产函数是建立在边际生产力理论中规模报酬递减规律的基础上,反映生产要素的投入和产出之间关系的函数模型。在工业经济时代,科技水平不高,资本和劳动力在生产环节发挥着极为重要的作用,这种投入只局限于资本和劳动力的投入,没有考虑其他投入因素的影响。在知识经济时代,知识对宏观经济增长和微观企业竞争的贡献是不言而喻的。在传统的新古典增长模型中,经济增长是由资本、劳动力投入和技术进步决定的,假定生产函数具有Cobb-Douglas形式(借鉴索洛改进的Cobb-Douglas生产函数),本文针对我国研发活动的实际情况,沿用Cubb-Douglas生产函数模型的形式,考察企业单纯的研发投入和单纯的研发产出,并且以引入有效发明专利这一变量来扩展Cubb-Douglas生产函数,模型设定如公式(1)所示:

其中,Y表示产出,A表示技术水平,K表示投入资本,I表示有效发明专利,L表示投入的劳动量,α表示有效发明专利的弹性系数,β表示资本的弹性系数,γ表示劳动力的弹性系数。
对公示(1)两边取对数,并引入随机误差项,构建计量模型如公式(2)所示:

其中,Y是新产品销售收入,A是初始技术水平,I是有效发明专利,K是新产品开发经费支出,L是研发人员当量,ε是随机误差项。
用英文字母代表公式(2)中的变量就得到简化的计量模型,如公式(3)所示:

其中,y表示对数化的新产品销售收入,a表示对数化的初始技术水平,i表示对数化的有效发明专利,k表示对数化的新产品开发经费支出,l表示对数化的研发人员当量,u是随机误差项。
(二)指标选取。借鉴已有代表性指标,本文选定新产品销售收入、研发活动人员全时当量、新产品开发经费支出、引进技术经费支出这四个指标。被解释变量为新产品销售收入,解释变量分别为新产品开发经费支出、研发人员当量、引进技术费用。
1.新产品销售收入。选取被解释变量为新产品销售收入,这类似于Cubb-Douglas生产函数中的产品数量Y,又不完全一样。Cubb-Douglas生产函数中的产品数量Y表示的是产成品的数量,如今这种度量生产产出的方法是片面的,因为这对于衡量很多企业特别是高新技术企业的产出是不合理的,高新技术企业的产出更多的表现为无形资产或者难以精确度量的智力资本存量。已有文献将企业净利润作为被解释变量即研发产出指标,但是笔者认为,净利润不仅反映了研发投入带来的收益,也包括了其他因素的影响,如利好的市场行情也有可能会大幅度提高净利润。所以,为了更好地研究研发投入与产出,我们只考虑新产品研发带来的收入即新产品销售收入。
2.有效发明专利。国外的研究是在成熟或发达的市场经济背景下进行的,无需考虑专利制度对创新的影响,因而强调非制度因素在创新中的作用。因我国市场经济的发展起步较晚,产权保护制度发展尚不完善,因此借鉴张炜(2014)和吴延兵(2006)的研究,本文引入有效发明专利指标作为解释变量。
3.新产品开发经费支出。该指标类似于Cubb-Douglas生产函数中的资本投入,但是Cubb-Douglas生产函数中的资本投入是广义的,包括了对机器、工具、设备和工厂建筑等的投资,是传统的资本投入范畴。本文研究的目的是着重考虑企业研发过程中的投入与产出,只考虑单纯的研发活动中的投入。而企业在研发投入时,新产品开发经费支出是其投入的一个主要方面,因为这往往决定了研发产出过程能否顺利进行,所以,我们有必要把新产品开发经费支出作为被解释变量之一即研发的投入指标。
4.研发人员当量。这类似于Cubb-Douglas生产函数中的劳动力数量。但是Cubb-Douglas生产函数中的劳动力数量指的是所有劳动力数量,包括了生产、销售等活动的劳动力数量,本文研究的是研发
过程中的投入与产出,所以研究过程中需要剔除研发活动之外的劳动力数量。并且由于现有的数据无法更好地将研发人员投入的成本量化,所以,本文就把研发人员的全时当量作为研发人员投入的指标。
相关指标的选取与界定如表1所示。
(三)数据选取。由于本文是从宏观角度探讨研发效应的,因而选取《中国科技统计年鉴 (2014)》中2000—2013年连续14年的统计数据。变量的描述性统计如表2所示,可知研发产出即新产品销售收入对数化后其离散程度较低,有较大的概率服从正态分布;研发投入之一即R&D人员全时当量对数化后其离散程度更低,有较大的概率服从正态分布;研发投入之二即新产品开发经费支出对数化后其离散程度较之前两指标较高,有较低概率服从正态分布;研发投入之三即专利保护,对数化后其离散程度较高,有较高概率服从正态分布。
四、实证结果与检验分析
(一)实证结果。通过Eviews 8.0版本的多元回归,最终得到实证结果如表3所示。
(二)结果检验。
1.模型对样本拟合优度的检验(可决系数R2)。可决系数是以回归平方和占总平方和的比例作为衡量模型对样本拟合优度的指标,且R2的值越接近于1,表明模型对样本拟合优度越高。在本模型中R2=0.99,这意味着99%可以通过所估计的投入产出函数来解释。
2.模型的显著性检验(F检验)。可决系数检验只能说明模型对样本数据的近似情况,而模型的显著性检验就是检验模型对总体的近似程度,在模型中,取显著水平 ω=0.05,F0.05(3,8)=4.07<1 263.914,所以认为模型的线性关系是显著的。
3.变量的显著性检验(t检验)。变量的显著性检验旨在对模型中解释变量和被解释变量之间是否存在线性关系做出推断。根据上文中的比较数据,t0.025(9)=2.26,所有变量均通过检验。
五、研究结论与政策建议

表1 变量选取及变量界定表

表2 相关描述性统计表
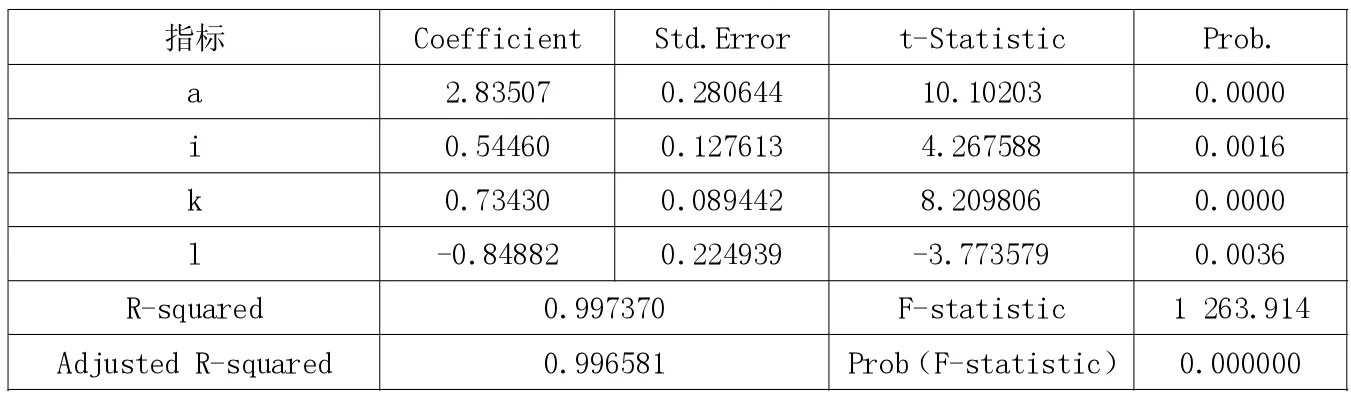
表3 实证结果分析表
(一)研究结论。本文利用2000—2013年的统计数据,指出了企业活动中其他因素的影响,从单纯的研发投入与产出的角度对我国企业研发投入情况进行了分析。研究发现,新产品开发经费支出对新产品销售收入影响显著,二者呈正相关,有效专利发明与新产品销售收入也呈显著正相关。在企业研发活动中,专利件数与研发投入、经营绩效间的关系显著 (黄世政,2015)。本文的研究结论认为,这种显著的关系可以在企业投入和产出之间形成很好的良性循环,即新产品开发经费支出和有效发明专利对新产品销售收入有着积极的影响。
研发人员全时当量与新产品销售收入显著负相关,与现实情况不符,一种解释是研发机构要对研发人员支付工资等,对新产品销售收入的增长有抵销作用,预期效果并没有反映出来。另一种解释是研发人力资源配置存在浪费现象。该结论与国际上对我国工业系统的研发效率研究结论基本一致。虽然研发经费支出处于不断增长的态势,但是从人均水平来看,仍然很低,造成了研发人力资源的浪费。再者,研发人力资源要素的市场配置机制正处于不断形成并发挥作用的过程中,研发人员的流动性在一定程度上受到限制,还不能有效实现以市场为导向的自由流动机制,从而也使得研发人力资源配置中存在一定的浪费现象。坚持科技资源配置中的市场化改革方向依然是解决问题的根本。
(二)政策建议。
1.企业应加大研发过程中对知识产权的申请保护。回归结果显示研发人员产出弹性系数:α=(∂Y/Y)/(∂I/I)=0.60812。专利是依据法律保护发明者的权利,可以在一定时期内占领市场的有利地位,并且取得一定的市场优势,有利于刺激研发人员进行一系列的研发活动。黄世政(2015)认为,在企业研发活动中,专利件数对研发投入与经营绩效间的关系具有中介作用。本文的研究结论认为,这种中介作用可以在企业投入和产出之间形成很好的良性循环。一方面,有效专利件数可以部分衡量研发投入,专利产权对新产品销售收入的促进作用;另一方面,有效专利件数也可以很好地衡量研发产出,这两方面的关系贯穿于整个研发活动,使得研发投入和产出活动可以高效进行。
2.企业应加大研发过程中的物质资本投入。回归结果显示新产品开发经费产出弹性系数为 β=(∂Y/Y)/(∂K/K)=0.601707,这表明新产品开发的经费支出对研发产出有着积极的影响,并且这种影响非常显著。所以,为了更好地实现企业研发产出的成果,顺利实现新产品带来的收益,企业应该提高研发过程中的物质资本投入。
3.企业应持续优化研发过程中的研发人员投入。回归结果显示γ=(∂Y/Y)/(∂L/L)=-0.69855,这表明,企业在研发的投入与产出过程中,研发人员的数量对研发产出有着消极的影响。我国的研发人员现状是总体上数量较少,研发能力较差(表现在回归后研发人员的相关系数较低),对研发产出有消极的影响。积极作用在本次宏观数据回归中没有体现出来,可能的原因有以下几点:第一,在我国整体科研能力较差的情况下,研发人员在研发过程中不能很好地体现其价值,甚至对研发过程有着消极的影响;第二,研发人员在研发投入与产出的过程中发挥着其他中介作用,研发人员并不能使研发产出立竿见影地增加;第三,研发人员在研发投入与产出的过程中有浪费,2005年我国人才浪费总规模已经超过2 500万人,导致经济消耗和经济损失超过9 000亿元,我国人才国际竞争力仅相当于美国的48%、日本的62%和德国的75%;第四,研发人员的市场流动机制不完善。所以,在国家层面,政府要完善研发人员的市场流通机制,使研发人员合理、有效地进行市场配置;在企业层面,企业本身要加大和优化研发人员的投入,保证企业在研发活动中发挥最大的效用;研发人员自身层面,要不断提高自身的科研能力。
