线性算子有界性的特征刻画
2015-09-16文生兰韩艺兵信息工程大学理学院郑州450001
文生兰,韩艺兵(信息工程大学理学院,郑州450001)
线性算子有界性的特征刻画
文生兰,韩艺兵
(信息工程大学理学院,郑州450001)
古典分析中的函数概念是指两个数集之间所建立的一种对应关系。现代数学的发展却要求建立两个任意集合之间的某种对应关系,即算子。算子是泛函分析中最重要的概念之一,研究算子的有界性是分析理论关注的首要问题,本文证明了关于线性算子有界性的一些等价命题。
有界线性算子;赋范线性空间;强弱收敛点列
算子与经典数学中的函数、映射是一回事。通常将两个空间之间的对应关系称为算子,它在微分方程、积分方程和工程技术领域有很广泛的应用。了解有界线性算子的特征,对进一步开展理论和应用研究有很大作用。在判断算子的有界性时,仅通过定义有时是很复杂甚至是行不通的,本文给出了判断算子有界性的一些简便且有效的方法。
1 预备知识
定义2设X、Y是同一数域K上的赋范线性空间,D是X的线性子空间,T是D到Y的有界线性算子,则称

为算子T的范数。
引理1X、Y是同一数域K上的赋范线性空间,D是X的线性子空间,T是D到Y的线性算子,则T的范数可表示为
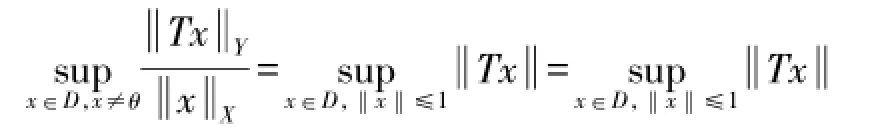
证明参看文献[1]。
引理2T:X→Y是线性赋范空间X到Y的线性算子,则下面命题等价
(1)T是有界线性算子;
(2)T是连续线性算子;
(3)存在x0∈T,使T在x0处连续;
(5)若{xn}⊂X,xn→x0,则T(xn)→T(x0)。
2 主要结果
定理1设X和Y都是赋范线性空间,T是X到Y的线性算子。假如∀g∈Y*,h(x)=g(Tx)是X上的有界线性泛函,则T是X到Y的有界线性算子。
证明∀x∈X,记Fx∈X**为x在自然映射下的像,则对x∈B(0,1)
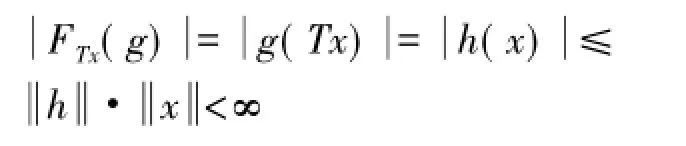
由共鸣定理知,T是X到Y的有界线性算子。
定理2设X、Y是赋范线性空间,T是X到Y的线性算子,则下列三个命题等价:
(1)T是X到Y的有界线性算子;
(2)T把X中的弱收敛点列映射为到Y中的弱收敛点列;
(3)T把X中的收敛点列映射为Y中的弱收敛点列。
证明(1)⇒(2):设在X中{xn}弱收敛于x,即对任何f∈X*,有f(xn)→f(x)。
又设g∈Y*,则T*g∈X*,所以T*g(xn)→T*g (x),即g(Txn)→g(Tx),Txn弱收敛于Tx在Y中。
(2)⇒(3):由于强收敛点列一定是弱收敛的,所以由(2)显然得(3)。
(3)⇒(1):设{xn}强收敛于点x在X中,且∀g∈Y*,g(Txn)弱收敛于g(Tx),即g在Tx连续,连续即有界,因此∀g∈Y*,h(x)=g(Tx)是X上有界线性泛函,由定理1知,T是X到Y的有界线性算子。
3 应用
例设X、Y是两个赋范线性空间,{Tn}n≥1⊂B (X,Y),假如在X中xn→x,而{Tn}n≥1在B(X,Y)中弱收敛于T。证明:Tnxn在Y中弱收敛于Tx。
证明已知Tn是有界线性算子,由定理2知: Tn将X中的(强)收敛点列xn→x映射为Y中的弱收敛点列:Tnxn弱收敛于Tnx。又由于{Tn}n≥1在B (X,Y)中弱收敛于T,即∀x∈X,Tnx弱收敛于Tx,从而Tnxn在Y中弱收敛于Tx。
[1]胡国恩,朱月萍,刘宏奎,等.应用泛函分析[M].西安:西安电子科技大学出版社,2012.
[2]张恭庆,林源渠.泛函分析讲义[M].北京:北京大学出版社,2006.
[3]程其襄,张奠宙,魏国强,等.实变函数与泛函分析基础[M].北京:高等教育出版社,2001.
[4]夏道行,吴卓人,严绍宗,等.实变函数论与泛函分析[M].北京:高等教育出版社,2010.
(责任编辑赵冰)
Characteristics of Depicting the Bounded Linear Operator
WEN Sheng-lan,HAN Yi-bing
(College of Science,Information Engineering University,Zhengzhou 450001,China)
Function in the classical analysis is established between two data sets.The development of modern mathematics needs to set up a corresponding relationship between two arbitrary collections,namely,operator.Operator is one of the most important concepts in functional analysis.The boundedness of the operator is a primary issue in the theory of analysis.This article gets some equivalent propositions about the boundedness of the linear operator.
bounded linear operator;normed linear space;strong and weak convergence sequence
10.13783/j.cnki.cn41-1275/g4.2015.01.030
O177
A
1008-3715(2015)01-0127-02
2014-10-21
文生兰(1981—),女,河南南阳人,信息工程大学理学院讲师,主要从事偏微分方程研究。
