拱形结构注浆控制煤矿采空区地表沉陷的机理初探

刘富有,刘应然,张 涛，詹亚辉，李雄峰

(1.河南省地质矿产勘查开发局第二地质矿产调查院,河南 郑州 450001； 2.中国地质大学(武汉)工程学院，湖北 武汉 430074)

拱形结构注浆控制煤矿采空区地表沉陷的机理初探

刘富有1,刘应然2,张 涛1，詹亚辉1，李雄峰2

(1.河南省地质矿产勘查开发局第二地质矿产调查院,河南 郑州 450001； 2.中国地质大学(武汉)工程学院，湖北 武汉 430074)

拱形结构注浆是一种新型的煤矿采空区注浆施工方法，该方法与采空区充填注浆的不同之处在于：它不仅从材料学角度加固地层，更重要的是结合结构力学原理，用拱形结构来承载上覆土压力和阻隔采空区上覆岩层变形向地表扩展。利用数学力学分析法和数值模拟法初步探讨了拱形结构注浆控制煤矿采空区地表沉陷的力学机理，得出了拱形结构注浆的相关注浆参数及其之间的数学关系，以及理想状况下的注浆效果,为进一步研究该注浆方法的关键技术奠定了基础。

煤矿采空区；地表沉陷；注浆；拱形结构；数值模拟

开采沉陷是地下矿产资源开采后周围围岩应力重分布过程中，上覆岩层和地表产生移动、变形和非连续破坏等的现象[1]。

截止2010年，我国煤矿采空区地面塌陷面积已累计达110万hm2，并以每年2.7万～4.1万hm2的趋势增加[2]。据2011年对山西省煤炭采空区的调查显示，采空区面积达3万km2，是山西全省面积的20%[3]。仅仅截止至2005年底，我国矿山开采引发的地质灾害已达12 000多处，死亡4 251人，造成的经济损失达161.6 亿元[4]。河南焦作市19处地面塌陷，造成的直接经济损失为9 435.6万元，潜在经济损失为42 249.88万元[5]。

目前采空区治理的方法主要有：巷道矸石回填、空区注浆充填、离层注浆充填、超高水材料注浆充填等。上述这些方法都存在钻孔费用高、回填工作量大、施工机械成本和材料成本较高等问题。采空区地表沉陷(也称地表塌陷)的治理其实质是要达到减少地表沉陷量，以此为目标需从减少钻孔工作量和材料用量的角度来降低采空区注浆的成本。为此，本文提出弯曲带拱形结构注浆的概念，该注浆方案不同于以往的注浆，它是一种以变换注浆孔孔底标高来形成预定拱形结构的弯曲带注浆方法。为成功实现这一注浆方案，需要进行注浆参数和注浆效果的研究，本文就这两个问题分别展开初步探讨。

1 采空区地表沉陷机理及拱形结构注浆概述

1.1 采空区地表沉陷机理概述

针对采空区地表沉陷机理，国内外许多学者进行了大量的研究。在国外，1885年，法国Fayol利用现场观测和模型研究，提出了开采沉陷的“拱形理论” ；1889年，豪斯提出了“分带理论”，认为采空区上方首先形成高度约为采厚的30～50倍的冒落裂隙综合带，其上为纯粹的弯曲带[6]；1903年，Halbaum将采空区上方的岩层看作是悬臂梁，导出地表应变与曲率半径成反比的结论；1913年，Fckardt得出采空区上方岩层的移动过程可视为各岩层逐渐弯曲的结构；1917年，俄罗斯M.M.普罗托吉亚科诺夫根据结构力学中的压力曲线理论提出了拱形冒落理论；1928年，德国哈克和吉列策尔提出压力拱假说，补充和完善了拱形冒落理论[7-9]；前苏联库兹涅佐夫提出了冒落岩块铰结理论。

在国内，钱鸣高等在20世纪80年代建立了采场薄板矿压理论，该理论将顶板岩层视为薄板，借用弹性力学中的薄板理论建立力学模型进行定量分析[10]；2009年，王晖在研究黄土地区的采空区塌陷机理时发现，松散层黄土的特殊节理结构、颗粒形态、粒间接触连接形式、孔隙等微结构特征使得松散层黄土的抗水稳定性能低，地表水的冲刷与下渗潜蚀作用促进冒落带和裂缝带高度达到松散层的黄土地表沉陷的形成[11]；王金安、马海涛等提出了采场上方存在高应力束组成的“复合应力拱”，“外应力拱”承担覆岩及地表土的自重并将其传递至采场两侧实体煤内，“内应力拱”主要承担悬空顶板的重量并传递至煤柱，“复合应力拱” 形态随时间推移而不断演化，“内应力拱”不断合并抬升直至与“外应力拱”重合，最终拱肩处岩体受拉压复合应力作用而首先开裂，从而破坏了“复合应力拱”成拱机制而导致采场上方覆岩断裂，形成地表塌陷[12-13]。

1.2 拱形结构注浆概述

拱形结构注浆是一种新型的煤矿采空区注浆施工方法,它利用浆液加固弯曲带岩土层，形成拱形结构(见图1)。该方法先在采空塌陷区外边界布设一圈边界孔，孔深应达到采空区裂隙带一定深度H0，以保证注浆拱有足够的稳定性。边界孔的注浆高度由两部分组成，即裂隙带内高度H0和弯曲带内高度H1。跨中孔注浆高度为H，为形成注浆拱，跨中孔相邻两孔孔底高程依次相差Δh，拱高为f，跨度为l,注浆扩散半径为R，其主要受注浆压力、地质条件等影响，可根据现场试验确定。注浆孔的间距为

a=2R-Δb

(1)

(2)

式中：Δb为注浆体的咬合宽度(m)；Fs为安全系数，一般大于1.0；Pmax为上覆岩土层的最大压力(kN)；σc为注浆结石体的抗压强度(kPa)。

拱形结构注浆主要参数说明见图2。

2 拱的简化力学模型

2.1 合理拱理论

拱形结构两端插入裂隙带基岩中，两端点在x方向和y方向都无位移；拱顶由于不是一体浇筑，可认为是铰接。因此，拱形结构注浆的拱可看作是三铰拱。

拱形结构的上覆荷载为岩土压力，为竖向荷载，平均重度为γ，拱顶岩土压力为qc，拱高为f，A、B、C分别为两个拱脚点和拱顶点，见图3。

当拱的压力线与拱的轴线重合时，各截面形心到合力作用线的距离为零，则各截面弯矩为零，从而各截面的剪力也为零，只受轴力作用，正应力沿截面均匀分布，拱处于无弯矩状态[14]。在不考虑侧向土压力的情况下，拱的任意截面弯矩为[14]

M=M0-FHy=0

(3)

式中：M0为代梁中相应截面的弯矩(kN/m2);FH为支座的水平推力(kN)。

对式(3)x微分两次，得

(4)

用q(x)表示沿水平线单位长度的荷载值，则有

(5)

所以

(6)

公式(6)中规定，y轴向上为正，y轴向下为负，坐标系选取见图3，故公式(6)可写为

(6)′

将q(x)=qc+γy代入式(6)′中，得

(7)

式(7)的微分方程的解答可用双曲线表示为

(8)

两个常系数A和B可由如下边界条件求得，即

在x=0处，y=0，得

在x=0处，dy/dx=0，得

B=0

因此合理拱曲线方程为

(9)

水平推力与拱高的关系式为

(10)

由此可见，在合理拱轴线的拱形结构中，水平推力FH为与跨度l和拱高f相关的一族曲线，只有当跨度l和拱高f同时确定时，水平推力FH才唯一确定。

当水平推力FH过大时，拱支座处就会产生剪切破坏,因此有

(11)

式中：Fτ为剪切破坏安全系数；τ为注浆结石体剪切强度(kPa)，τ=(qc+γh)tanφ+c;Ae为拱形结构注浆体支座剪切面有效面积(m2)。

当水平推力FH的最大值确定后，根据塌陷区的范围确定注浆拱布设为单跨或者多跨并确定跨度l，之后根据式(10)确定注浆拱的拱高f。

2.2 拱的挠度模型

合理拱不受弯矩和剪力作用，只受轴力作用，因此其变形的平衡微分方程可表示为

(12)

其中

(13)

(14)

式中：Δ为竖向变形(mm)；θ为转角(°)；FN为沿拱轴线方向各截面的轴力(kN)；E为注浆结石体弹性模量(MPa)；A为沿拱轴线方向各截面的面积(m2)。

3 拱形结构注浆控制地表沉陷的机理

3.1 概率积分法计算地表沉陷

概率积分法属于影响函数法，是介于经验方法和理论方法之间的一种方法，是在岩层移动的随机介质理论基础上，由我国学者经过多年的研究发展而来，因其所用的岩层和地表的移动和变形预计公式中含有概率积分而得名。该法具有计算模型简单、参数选取方便等优点，目前已成为我国较成熟的、应用最为广泛的岩层和地表的移动和变形预计方法之一[6]。

概率积分法是以随机介质理论为基础，通过模拟试验从统计规律出发，采用非连续介质模型，建立地表及覆岩的位移函数，其实质是根据理论研究或其他方法确定地下微小单元的开采对地表和覆岩的影响，把地下整个矿体的开采对上覆岩层和地表的影响看作是开采区内所有微小单元开采影响的总和，并据此计算整个开采引起的岩层和地表的移动和变形。概率积分法的数学表达式为

(15)

其中

rz=r(z/H)n,r=H/tanβ

式中:we(x,z)为单元开采引起的下沉(m);r为主要影响半径(m)；z为煤层顶板至计算平面的距离(m)；H为开采深度(m)；β为主要影响角(°)；n为与岩相关的系数，理论值为2πbtanβ,一般取0.5～0.9。

假设煤层开采在走向方向的长度为L，根据积分原理，则地表任意点(x,y)处的下沉量为

(16)

其中

w0=wmax=ηmcosα

式中:w0为煤层顶板下沉量(m)；m为煤层开采厚度(m)；η为下沉系数，取值与覆岩岩性、顶板管理方法等因素有关;α为煤层倾角(°)。

3.2 注浆前后地表下沉量计算

注浆前地表下沉量计算公式为

(w0)x=f(x,r,s,η,b,θ)

(17)

式中：(w0)x为开采前地表x点下沉值；f为概率积分函数；r、s、η、b、θ分别为主要影响半径、拐点偏距、下沉系数、水平移动系数、开采影响传播角。

注浆后由于浆液在弯曲带内的岩土层形成的是拱形结构，即使当拱形结构下面岩土层发生弯曲变形与拱结构脱离，只要拱结构的稳定性不遭受破坏，拱结构上覆岩土体的变形就不会受到采空区的影响。此时，地表变形只与上覆岩土体作用在拱结构上的土压力使其发生的竖向变形有关,其变形量可用式(13)和(14)来计算。

3.3 控制地表沉陷的数值模拟

为探讨拱形结构注浆对地表沉陷的减沉效果，本文以河南焦作市某煤矿采空区独特的工程地质条件为例，抽象出表1所示的地层概况，建立一个平面应变模型，分别模拟该煤矿采空区未注浆、普通充填注浆和拱形结构注浆地表沉陷的情况。

平面应变模型在长度方向取1 000 m，高度取300 m，厚度取1 m；厚度方向上取1个单元，长度方向上取100个单元，高度方向上根据地层不同单元长度不同；共建立7 600个单元，15 554个节点;采空区位于长度方向上的400～600 m，见图4。模型地层情况及岩土参数见表1，采空区注浆材料参数见表2。为具有可比性，假设普通充填注浆与本文提出的拱形结构注浆材料参数相同。拱形注浆结构利用FISH语言编写的命令建立起始点高度呈悬链线方程变化的桩单元来模拟，桩单元参数见表3。

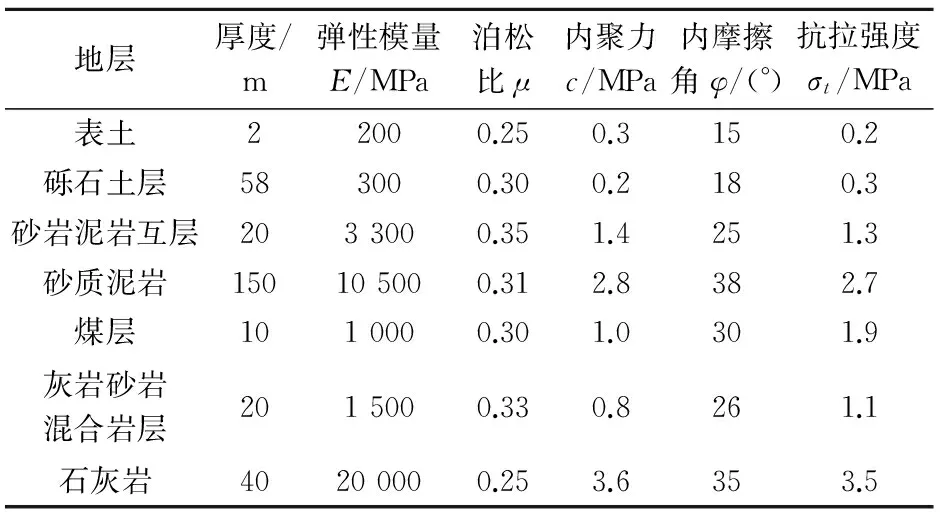
地层厚度/m弹性模量E/MPa泊松比μ内聚力c/MPa内摩擦角φ/(°)抗拉强度σt/MPa表土22000.250.3150.2砾石土层583000.300.2180.3砂岩泥岩互层2033000.351.4251.3砂质泥岩150105000.312.8382.7煤层1010000.301.0301.9灰岩砂岩混合岩层2015000.330.8261.1石灰岩40200000.253.6353.5

表2 注浆材料参数

未注浆、普通充填注浆、拱形结构注浆采空区地表沉陷等值线数值模拟结果见图5、图6和图7。采空区拱形结构注浆与未注浆、普通充填注浆的减沉效果对比见图8。

表3 数值模拟中桩单元参数

拱形结构注浆相当于注浆体与地下破碎松散岩土层固化形成拱形结构的注浆桩。由数值模拟结果(见图5、图6和图7)可以看出，未注浆时采空区地表沉陷最大深度为171 mm，普通充填注浆后采空区地表沉陷最大深度为35 mm，拱形结构注浆后采空区地表沉陷最大深度为21 mm，可见拱形结构注浆这种治理采空区地表沉陷的方法是可行的，它可以起到减小采空区地表沉陷的作用，且与普通充填注浆相比，它还可以减小塌陷盆地的面积。

减沉率r指采空区注浆与不注浆相比,地表最大下沉量的减少值与不注浆时地表下沉量的比值[18]。经计算可知，采空区普通充填注浆减沉率为r=87.7%，采空区拱形结构注浆减沉率为r=94.7%，说明本文所提出的拱形结构注浆方法减沉效果明显，可以进行现场试验。

4 结 论

拱形结构注浆是一种新型采空区注浆施工方法，它利用拱结构在合理拱轴线布置下不受弯矩和剪力影响，只受轴力影响的特点，充分发挥了岩土材料的抗压强度作用，来控制采空区地表沉陷。只要施工工艺合理、注浆参数满足要求、材料力学性能达到设计要求，是能够承受上覆土压力甚至附加压力，从而达到减沉的目的。

拱形结构注浆是采空区注浆施工中的一种新方法，还有许多问题需要进一步的研究，比如该方法所适用的地质条件、注浆深度、注浆扩散半径、相邻注浆桩的咬合宽度、注浆材料的力学性质，甚至其长期稳定性等。

[1] 何国清，杨伦，凌赓娣，等.矿山开采沉陷学[M].徐州：中国矿业大学出版社,1991.

[2] 王彬,邓瑞杰,谭松,等.我国煤矿地面塌陷分析与防治[J].陕西煤炭,2010(3):69-70.

[3] 胡展奋,高勤荣.血色黑洞 山西煤炭采空区现状调查[J].新民周刊,2011(43):28-37.

[4] 张进德，张作辰，刘建伟,等.我国矿山地质环境调查研究[M].北京：地质出版社，2008.

[5] 张伟.焦作市区地面塌陷发育特征、成因及对策建议[J].矿产保护与利用,2007(4):45-48.

[6] 徐乃忠，张玉卓.采动离层充填减沉理论与实践[M].北京：煤炭工业出版社,2001.

[7] 王建学.开采沉陷塑性损伤结构理论与冒矸空隙注浆充填技术的研究[D].北京：煤炭科学研究总院,2001.

[8] 刘书贤.急倾斜多煤层开采地表移动规律模拟研究[D].北京：煤炭科学研究总院,2005.

[9] 王明立.急倾斜煤层开采岩层破坏机理及地表移动理论研究[D].北京：煤炭科学研究总院,2008.

[10]孙超,薄景山,孙有为.采空区沉陷研究历史及现状[J] 防灾科技学院学报,2008,10(4):128-131.

[11]王晖.青兰高速公路沿线北八特区采空区地表沉陷机理及其数值模拟[D].北京：中国地质大学(北京)，2009.

[12]王金安,赵志宏,侯志鹰.浅埋坚硬覆岩下开采地表塌陷机理研究[J].煤炭学报,2007(10):1051-1056.

[13]Ma H T,Wang J N,Wang Y H.Study on mechanics and domino effect of large-scale goaf cave-in[J].SafetyScience，2012，50：689-694

[14]龙驭球，包世华.结构力学Ⅰ基本教程[M].北京：高等教育出版社,2006:87-91.

[15]王平.合理拱理论及其在无衬砌隧道可靠性分析中的应用[D].重庆：重庆大学,2013：19-20.

[16]梁昌望,高冰松,瞿尔仁.拱的挠度理论分析[J].合肥工业大学学报(自然科学版),1998(5):52-56.

[17]贺栓海.拱桥挠度理论[M].北京：人民交通出版社,1996.

[18]廖俊展.注浆减沉条件下的覆岩与地表移动规律研究[D].青岛：山东科技大学,2004：57.

[19]段瑜,赵培,宁齐元,等.非煤矿山采空区失稳机理及稳定性数值模拟分析[J].安全与环境工程,2014，21(6):29-35.

Study on the Mechanism of Subsidence Control with Arch Structure Grouting in Coalmine Gob Area

LIU Fuyou1,LIU Yingran2,ZHANG Tao1，ZHAN Yahui1，LI Xiongfeng2

(1.No.2InstituteofGeological&MineralResourcesSurveyofHenan,Zhengzhou450001，China； 2.FacultyofEngineering,ChinaUniversityofGeosciences,Wuhan430074,China)

The arch structure grouting is a new-type grouting method in mine gob which is different from the filling grouting in gob area in that it not only reinforces stratum from view of materials science,but more importantly,it combines structure mechanics principle and uses the arch structure to carry the top soil pressure and to obstruct extension of overlying rock transformation towards surface.This article explores the mechanical mechanism and obtains correlation parameters of the arch structure grouting and mathematic relation between each other, and the grouting effect under ideal conditions. The study establishes the basis for the further study of the key technology of the arch structure grouting method.

coal mine gob area;subsidence;grouting;arch structure;numerical simulation

1671-1556(2015)04-0022-06

2014-12-17

2015-06-24

刘富有(1968—)，男，硕士，教授级高工，主要从事矿山地质环境方向的研究工作。E-mail:15038212888@139.com

X45

A

10.13578/j.cnki.issn.1671-1556.2015.04.004