一种减轻纯电动中巴前悬轮胎磨损的优化方法*
2015-09-13袁炜彬陈新度夏鸿建熊会元吴义忠广东工业大学广东省计算机集成制造重点实验室广东广州50006东莞中山大学研究院广东东莞5000华中科技大学国家CAD支撑软件工程技术研究中心湖北武汉40074
袁炜彬,陈新度,夏鸿建,熊会元,吴义忠(.广东工业大学广东省计算机集成制造重点实验室,广东广州50006;.东莞中山大学研究院,广东东莞5000;.华中科技大学国家CAD支撑软件工程技术研究中心,湖北武汉40074)
一种减轻纯电动中巴前悬轮胎磨损的优化方法*
袁炜彬1,陈新度1,夏鸿建1,熊会元2,吴义忠3
(1.广东工业大学广东省计算机集成制造重点实验室,广东广州510006;2.东莞中山大学研究院,广东东莞523000;3.华中科技大学国家CAD支撑软件工程技术研究中心,湖北武汉430074)
纯电动中巴悬架系统通常以传统中巴悬架为设计基础,但由于其质量及外形结构的变化,易产生轮胎磨损严重等问题。以某纯电动中巴的双横臂前悬架为对象,以减轻轮胎磨损为目标,对其硬点作灵敏度分析,辨识影响悬架性能的关键参数。采用RBF构造响应面,通过遗传算法寻优,对悬架的外倾角、前束角及轮心侧向位移量进行多目标综合优化。结果表明,悬架性能获得显著提升,有效减轻轮胎磨损。
轮胎磨损;敏度分析;RBF;遗传算法
0 前言
纯电动汽车作为一种新能源汽车,相对于传统汽车而言,以电池包取代油箱,以电动机取代了发动机,且通常不需要变速装置。在实际纯电动汽车研发时,为提高研发效率,通常采用传统汽车底盘系统作为设计基础。然而由于纯电动汽车电池组数目多且质量大,直接在传统汽车底盘基础上开发纯电动汽车,其底盘性能难以满足车辆动力学性能要求。
悬架系统作为车身与路面相互作用的媒介,是决定汽车是否行驶平顺和操作稳定的基础。悬架设计的不合理,容易导致轮胎在跳动的过程中前束角与外倾角变化过大,这是轮胎磨损过快的主要原因[1],也是急需解决的关键问题。在行驶过程中,轮胎磨损过快或异常,直接影响整车性能及乘车安全。文献[1]通过研究前轮定位参数与轮胎磨损的关系,得出轮胎磨损做功的理论模型,但过多的变量数及优化的约束函数不仅降低优化效率,而且增大了实际生产中的改进成本。为改进并提高悬架运动特性,文献[2]采用有限转动张量,结合矢量代数法,建立悬架运动学数学模型从而优化悬架性能,计算过程相对复杂,不利于实际应用。文献[3]以样车前轮K&C特性曲线的斜率为目标,通过ADAMS/Insight对悬架硬点灵敏度分析及优化,但斜率的改变不能直观地反映目标函数的变化范围及优化后的性能优劣。文献[4]应用遗传算法优化以二次多项式构造的响应面目标函数,寻优效率不高,且由于通常设计目标存在强非线性,二次多项式难以获得较高精度。
为此,本文结合某实体样车数据,建立扭杆式双横臂独立前悬架的虚拟样机模型,通过对悬架的硬点进行灵敏度分析,继而采用中心复合试验设计方法,以更适合求解非线性目标的径向基函数(RBF)构造响应面模型,利用遗传算法进行寻优。
1 双横臂悬架系统建模
为了保证纯电动中巴的续航性能,在有限的空间里安装足够的电池包,考虑到自身车重及前后悬架簧上载荷的比重等因素,中巴采用了后轮驱动,并选用了扭杆式双横臂独立前悬架。通过对纯电动中巴扭杆式双横臂独立前悬架的硬点测量,得到建立双横臂悬架虚拟样机模型的基本数据,根据系统各运动机构和约束杆件之间链接的运动学和动力学特性的本质,将实际车体样车悬架系统作一定程度的简化,绘制双横臂悬架结构示意图,如图1所示。部分悬架参数及前轮定位参数见表1所示,主要硬点坐标值见表2所示。

图1 双横臂悬架结构示意图

表1 部分悬架参数及前轮定位参数
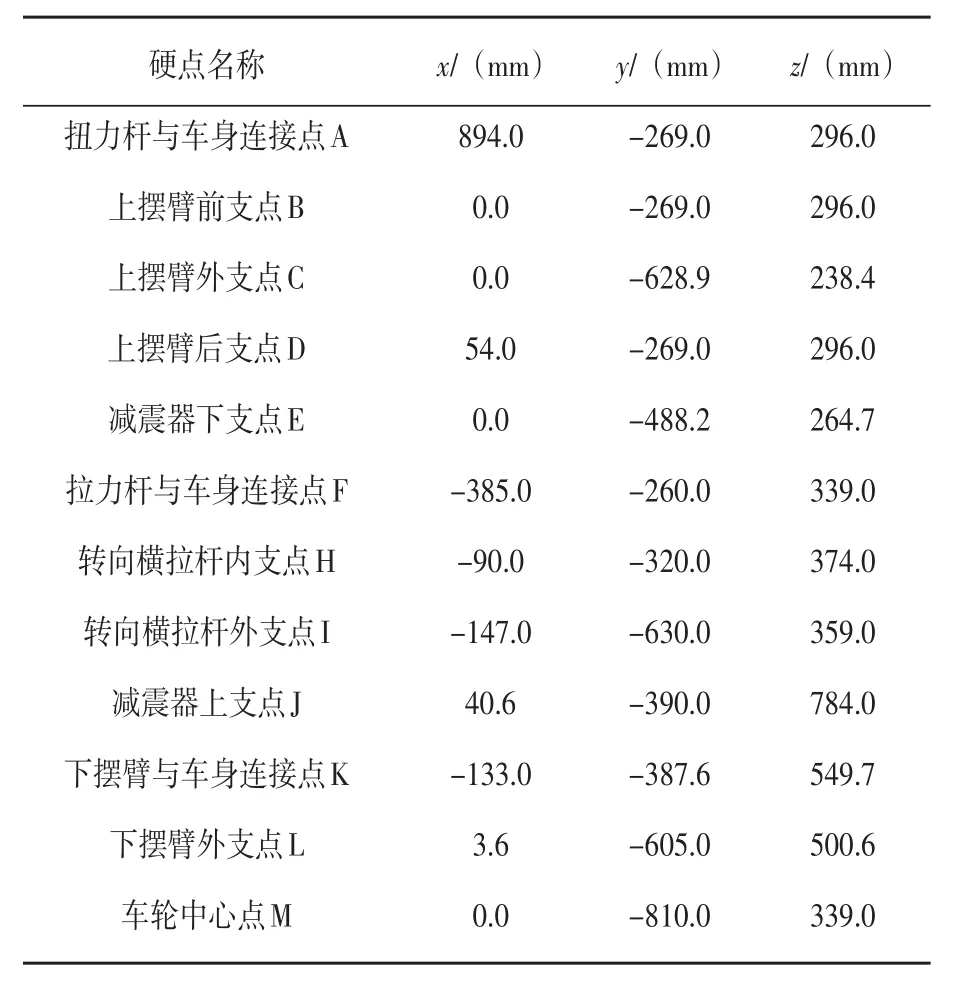
表2 悬架主要硬点坐标值(左侧)
2 车轮定位参数的悬架灵敏度分析
2.1性能评测目标
为了提高设计效率,本文通过对悬架的硬点进行灵敏度分析,挑选对目标函数灵敏度高的硬点坐标作为设计变量。影响轮胎磨损的主要因素是作用于轮胎的侧向力和胎面力矩,一般情况下出现早期异常磨损是因为外倾角和前束角的不合理搭配所导致[5]。因此,这里选择较能反映轮胎磨损做功特性的车轮前束角Cθ、车轮外倾角Cψ以及轮心侧向位移量Cω作为优化目标。设置B1=作为三个敏度分析目标函数。
2.2灵敏度分析与参数选取
灵敏度分析是指研究与分析一个系统(或模型)的状态或输出变化对系统参数或周围条件变化的敏感程度的方法。通过灵敏度分析可以了解哪些参数对悬架结构有较大的影响。若通过改进车架与转向系统的结构以达到减轻轮胎磨损,会导致设计的周期过长,人力和生产成本显著提升。故不宜对悬架与车身连接点、转向机构y向的长度作出修正,为此,本文选取了转向横拉杆内支点H(x,z)方向点,转向横拉杆外支点I(x,y,z)方向点,上摆臂外支点C(x,y,z)方向点,下摆臂外支点L(x,y,z)方向点的11个坐标值作为设计变量,设定每个坐标值的变化范围在-10~10mm之间。选择两水平试验为DOE设计类型,选用部分因子试验(Fractional Facto⁃rial),一共进行32次迭代仿真。如图2~图4所示为设计变量对车轮前束角、车轮外倾角以及侧向滑移量的灵敏度。
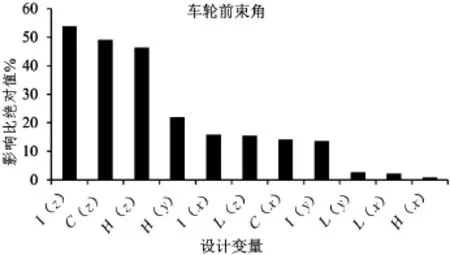
图2 车轮前束角的灵敏度分析

图3 车轮外倾角的灵敏度分析
2.3关键设计变量的选取
由图2~图4的灵敏度分析数据可得,上摆臂的外支点C(z)、转向横拉杆外支点I(x,z)及转换横拉杆内支点H(z)对车轮前束角、外倾角及轮心滑移量的变化影响显著。但为了节约悬架的改造成本及减少优化周期,以及保留悬架原设计中主销内倾角与主销后倾角的运动特性,应尽量减少需要改动的部件,尤其是上、下摆臂。因此本文选取I(x,z)和H(z)这三个悬架参数作为关键的设计变量,矩阵表示为:
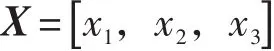
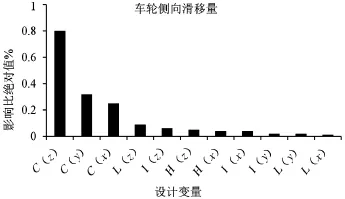
图4 轮心侧向滑移量的灵敏度分析
3 响应面法拟合目标函数
对以上三个变量设定变化范围及确定编码水平,如表3所示。
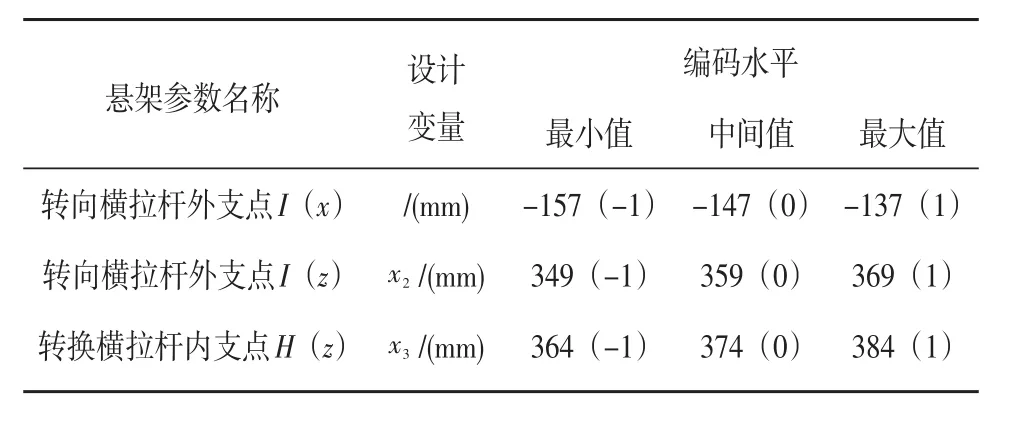
表3 设计变量编码水平
由于设计变量与目标存在严重的非线性关系,难以直接通过多项式函数拟合,故选用径向基函数模型(RBF)构造响应面函数公式,见式(1):

其中,基函数有N个在函数空间上的样本点与X相关联后的径向函数构成,λj为每个基函数的权重,求函数空间就归结为求权重系数λj[6]。

其中,i为变量数,j为试验次数,c为正实数。
选取中心复合设计法(CCDs)中精度较高的外切中心复合设计[8](CCC)作为实验设计方法,取中心点数为2,星号臂α为1.29,以代码的形式编排试验表,如表4所示。经过16次反复应用ADAMS/Car模块对每个设计组合进行平行车轮跳动(ParallelWheel Travel)仿真,车轮上下跳动的范围为(-60 mm,60 mm),计算出B1、B2、B3,并记录在表4中。

表4 设计变量与目标响应的实验设计
按照中心组合试验设计结果,根据径向基函数模型构造响应面函数公式(1)和Multi-Quadric函数公式(2),得出以下三个目标函数的表达式,见式(3)、式(4)、式(5)。

其中:
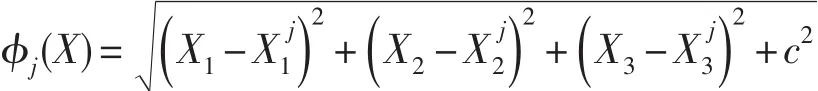
其中,当c≤1/n时,文献[9]发现响应面模型逼近的效果最好,故c取0.06。
在求解权重系数λij过程中,若用矩阵表示,此问题等同于解线性方程,见式(6),得λij,结果如表5所示。


表5 λij计算结果
4 遗传算法优化及结果分析
4.1优化模型
在使用遗传算法对多目标优化时,本文采用权重系数变换法,利用单目标优化的遗传算法求解多目标优化问题[10]。首先对以上的三个子目标响应(B1、B2、B3)赋予权重ωi,其中ωi反映相应的子目标在多目标优化问题中的重要程度,再将三个子目标响应统一为遗传算法适应度函数,见式(7)。从文献[1]可知,车轮前束角带来的轮胎磨损远比车轮外倾角以及轮心侧向位移量带来的严重,经过反复调整遗传算法适应度函数中的权重系数,取ω1=0.6,ω2=0.2,ω3=0.2。
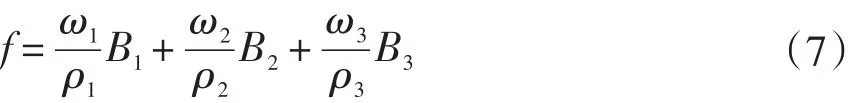
其中:ω1、ω2、ω3为各子目标的权重;ρ1、ρ2、ρ3为比例系数,为各子目标在约束范围内的极值差,用以消除单目标函数间的量纲和数量级差异。
对适应度函数进行迭代,设定设计变量的编码水平为(-1,1),种群数为20,选用“锦标赛”选择机制,变异概率为0.05,交叉概率为0.6,最大迭代次数为200次,迭代过程的初始值随机产生。经过软件运算得出最优解为(-0.65,-1,1),从而得到优化前后设计变量的数值对比,见表6。

表6 优化前后设计变量的数值对比
4.2结果对比分析
分别将悬架优化前后的硬点数据输入AD⁃AMS/Car模块建立的虚拟样机模型中,见图5,得出优化模型,再进行平行车轮跳动仿真分析,车轮上下跳动范围为(-60mm,60mm)。优化后悬架的特性曲线与样车悬架特性曲线如图6~图8所示,其中优化后悬架的特性曲线由虚线表示,样车悬架特性曲线有实线表示。

图5 双横臂前悬架的虚拟样机模型
由图6和图8可得,优化后,前束角与轮心侧向位移量曲线趋势变得更加平缓,都缩小了前束角与轮心侧向位移量随车轮跳动时的变化范围。其中前束角的变化范围由原来的(-4.366 5°,2.210 6°)变为(-1.926°,0.485 8°),变化量缩小了63%。

图6 车轮前束角与车轮垂直位移的关系曲线

图7 车轮外倾角与车轮垂直位移的关系曲线

图8 轮心侧向位移量与车轮垂直位移的关系曲线

图9 阿克曼误差与左车轮转角的关系曲线
为了更好地描述优化后模型,轮胎磨损的减轻程度,这里引入阿克曼误差[11]进行优化前后的对比分析,如图9所示。由于阿克曼误差的存在,从而使轮胎的拖滑增加,加剧了轮胎磨损。从图9可知,在常用角度范围(0°~25°)内,阿克曼误差减少了10%,可以认为悬架的梯形机构设计更优。同时,由图7可得,外倾角在车轮上跳时的变化范围有所增大,在整个跳动过程中前束角和外倾角的匹配范围更大,且三个被测目标随车轮上下跳动变化的范围都更加合理,有助于减轻前轮磨损,符合优化要求。
5 结论
针对纯电动中巴扭杆式双横臂前悬架前轮轮胎磨损严重的情况,运用ADAMS软件的Car模块建立双横臂前悬架的虚拟样机模型,在Insight模块中对悬架硬点进行灵敏度分析,确定影响前轮轮胎磨损的关键硬点。应用中心复合设计法作为实验设计方法,结合径向基函数(RBF)拟合响应面适应度函数,运用遗传算法对悬架跳动过程中车轮前束角、车轮外倾角和轮心侧位移变化进行多目标优化设计,从而达到减轻前轮轮胎磨损的目的。通过对双横臂前悬架的仿真优化分析,进一步地了解该悬架的运动特性,为后续开发生产车型的悬架设计提供参考。
[1]唐应时,朱位宇.基于轮胎磨损的悬架与转向系统硬点优化[J].现代制造工程,2013,35(7):640-653.
[2]丁飞,韩旭.悬架导向机构硬点灵敏度分析及多目标优化设计[J].现代制造工程,2010,32(2):137-142.
[3]宋晓琳,毛开楠.麦弗逊前悬架硬点参数的灵敏度分析和优化[J].现代制造工程,2011(6):106-110.
[4]郭丽娜.悬架对汽车稳态回转性能的影响分析及其优化设计[D].南京:江苏大学,2012.
[5]钱立军.基于减少轮胎磨损的客车前轮定位参数优化[J].汽车技术,2011(2):14-17.
[6]吴义忠.多领域物理系统的仿真优化方法[M].北京:科学出版社,2011.
[7]R.L.Hardy.Theory and applications of the multiquad⁃ric-biharmonic method,20 years of discovery 1968-1988[J].ComputersMath.Appl,1990,19(8/ 9):163-208.
[8]张志红.在响应曲面方法中三类中心复合设计的比较研究[J].沈阳航空工业学院学报,2007,24(1):87-91.
[9]李艳.径向基函数及其应用[D].大连:大连理工大学,2009.
[10]胡贵强.多目标优化的遗传算法及其实现[J].重庆文理学院学报,2008,27(5):12-15.
[11]朱彪.基于轮胎磨损的前悬架和转向系统联合优化设计[D].长沙:湖南大学,2011.
(编辑:向飞)
An Optim ization M ethod to A lleviate TireW ear of Front Suspension on Pure Electric Bus
YUANWei-bin1,CHENXin-du1,XIAHong-jian1,XIONGHui-yuan2,WUYi-zhong3
(1.Guangdong University of Technology,Key Laboratory ofComputer Integrated Manufacturing System ofGuangdong Province,Guangzhou510006,China;2.Institute ofDongguan Sun Yat-sen University,Dongguan523000,China;3.Huazhong University ofScienceand Technology,NationalCADSupportSoftware Engineering Research Center,Wuhan430074,China)
Pure electric bus suspension system usually adopts traditional bus suspension as design basis,butdue to changes in the quality and structure,easy to produce the tire wear serious problem.In a pure electric bus double wishbone front suspension as the object,in order to reduce tirewear as the goal,for the sensitivity analysisof the hard point,key parameters identification of influence of suspension performance.Using RBFmethod to construct the response surface,optimized by genetic algorithm,multi objective optimization of the suspension camber angle,toe angle and lateral displacement of wheel center.The optimization results show that the suspension performance can be improved,effectively reduce the tirewear.
tirewear;sensitivity;RBF;genetic algorithm
U463.33+1
B
1009-9492(2015)04-0052-05
10.3969/j.issn.1009-9492.2015.04.014
*东莞市重大科技专项(编号:2011215155);国家自然科学基金青年基金(编号:51105079);广东省自然科学基金(编号:S2011040003989);校博士启动基金(编号:405120087)。
2015-01-26
袁炜彬,男,1989年生,广东东莞人,硕士研究生。研究领域:动力学仿真与优化。
